Декартова и полярная системы координат кратко

Обновлено: 05.07.2024

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O . Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.

Прямые с началом O , имеющие направление и масштаб, называют координатной прямой или координатной осью.

Прямоугольная система координат обозначается O x y . Координатными осями называют О х и О у , называемые соответственно ось абсцисс и ось ординат.

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех О х , О у , О z осей. Это три взаимно перпендикулярные прямые, где О z имеет название ось аппликат.

По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке O , называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте О х против часовой стрелки на 90 ° ее положительное направление совпадает с положительным О у , тогда это применимо для положительного направления О z . Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y , а средний за Z .

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку М на координатной оси О х . Любое действительное число x M равняется единственной точке М , расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если - 3 , то соответственное расстояние 3 . Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М , расположенная на O x , равна действительному числу x M . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении O x и О у . Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

Возьмем точку как проекцию точки M x на О х , а как проекцию точки M y на О у . Значит, через точку М можно провести перпендикулярные осям О x и О у прямые, где послучим соответственные точки пересечения M x и M y .

Тогда точка M x на оси О х имеет соответствующее число x M , а M y на О у - y M . На координатных осях это выглядит так:

Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел ( x M , y M ) , называемую ее координатами. Абсцисса M – это x M , ордината M – это y M .

Обратное утверждение также считается верным: каждая упорядоченная пара ( x M , y M ) имеет соответствующую заданную в плоскости точку.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Определение точки М в трехмерном пространстве. Пусть имеются M x , M y , M z , являющиеся проекциями точки М на соответствующие оси О х , О у , О z . Тогда значения этих точек на осях О х , О у , О z примут значения x M , y M , z M . Изобразим это на координатных прямых.

Чтобы получить проекции точки M , необходимо добавить перпендикулярные прямые О х , О у , О z продолжить и изобразит в виде плоскостей, которые проходят через M . Таким образом, плоскости пересекутся в M x , M y , M z

Каждая точка трехмерного пространства имеет свои данные ( x M , y M , z M ) , которые имеют название координаты точки M , , x M , y M , z M - это числа, называемые абсциссой, ординатой и аппликатой заданной точки M . Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел ( x M , y M , z M ) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.

Прямая, на которой указано направление, начало отсчета и масштаб называется числовой осью. Прямоугольная (декартова) система координатна плоскости состоитиз двух взаимно перпендикулярных числовых осей, пересекающихся в точке O – начале системы координат. Горизонтальную ось называют осью абсцисс, а вертикальную - осью ординат.

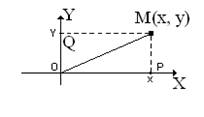
Каждой точке плоскости M сопоставляется ориентированный отрезок OM (радиус-вектор с началом в точке О и концом в точке M. Спроектируем точку М на оси координат (рис.1.1). Каждой точке плоскости M сопоставляется упорядоченная пара чисел (х,y), которые называются декартовыми координатами точки М(х,у). В любой системе координат существует взаимнооднозначное соответствие между точкой и ее координатами. На плоскости расстояние d между двумя точками M(х_i,y_i) и N(x_j,y_j) измеряется по прямой и вычисляется по формуле длины вектора

Пример. Найти расстояние d между двумя точками M(-3,4) и N((5.2). Согласно формуле (1.1) имеем

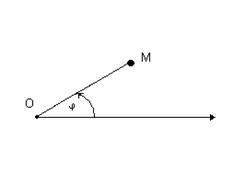
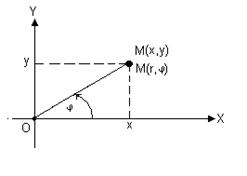
Полярная система координат. Выберем на плоскости фиксированную точку O, называемую полюсом, и исходящую из нее полуось OP, называемую полярной осью. На полярной оси указываем единицу масштаба. В этой системе координат (рис.1.2) положение точки M задается ее расстоянием r до полюса (т.е. длиной отрезка OM, называемого полярным радиусом точки M) и углом j, который составляет полярный радиус с полярной осью (положительный отсчет угла идет против часовой стрелки), причем -p 2 + y 2 = r 2 (cos 2 j+ sin 2 j)= r 2 . (1.3)

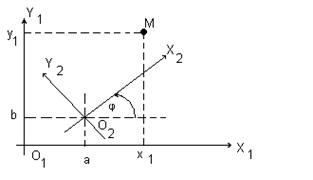
Преобразование системы координат.Пусть даны две прямоугольные системы координат X₁Y₁ и X₂Y₂ (рис.1.4 а). Найдем связь координат точки M(x₁,y₁) в одной из систем координат с ее же координатами (x₂,y₂) в другой системе. Для этого вначале совместим начала координат, сохраняя старые направления осей (рис.1.4 б), потом одну из систем повернем так, чтобы оси совпали направления координат.

Параллельный перенос системы координат. В первой системе координат точка O₁ имеет координаты (0,0), точка O₂ - (а,b), а точка M - (x₁,y₁). Рассматривая проекции этих точек на оси координат первой системы имеем

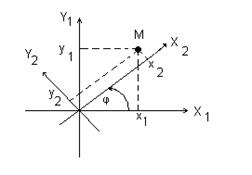
Чтобы получить координаты во второй системе, необходимо провести обратные действия. Это приведет к зависимостям

Поворот системы координат с совмещенной точкой начала. Пусть оси OX₁ и OX₂ повернуты на угол j. Из рис. 1.4 б следуют соотношения

В общем случае связь между координатами точки в различных прямоугольных системах координат выражается линейными соотношениями

Пример. Как изменятся координаты точки M(-2,3), если система будет повернута на 30 0 и сдвинута вверх на две единицы?

Применяя формулы (1.7) для x₁= -2, y₂ = 3, угла j = 30 0 , а =0 и b = 2, имеем

x₂ = -2cos30 0 + 3sin30 0 = -2 + 3 = -

y₂ = 2sin30 0 +3cos30 0 - 2 = 2 + 3 -2 = - 1

Глава 1. Геометрия на плоскости

Пример. Найти расстояние d между двумя точками M(-3,4) и N((5.2). Согласно формуле (1.1) имеем

Применяя формулы (1.7) для x₁= -2, y₂ = 3, угла j = 30 0 , а =0 и b = 2, имеем

Д екартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.

Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая из координатных осей называется осью абсцисс, вторая - осью ординат.

( см. рис. 1), где и суть проекции точки М на оси Ох и Оу, обозначает величину отрезка оси абсцисс, - величину отрезка оси ординат. Число х называется абсциссой точки М, число у - ординатой этой же точки. Символ М(х; у) обозначает, что точка М имеет абсциссой число х, а ординатой число у.

Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая - левой. Точно так же ось Оу разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй - лежащая в левой и в верхней полуплоскости, третьей - лежащая в левой и в нижней полуплоскости, четвертой - лежащая в правой и в нижней полуплоскости.

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Полярными координатами произвольной точки М (относительно заданной системы) называются числа и (см. рис.). Угол при этом следует понимать так, как принято в тригонометрии. Число называется первой координатой, или полярным углом точки М ( называются также амплитудой).

Полярный угол имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида , где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам , называется главным.

В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом,

2). При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу - вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки).

При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам

При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.

Человеку всегда было важно понять свое место в окружающем мире. Причем не только в пространстве, но и во времени, и в социуме. Оставим в стороне время и социум, это тема отдельного большого разговора. Сосредоточимся на пространстве. Как определить свое местоположение, местоположение других людей и окружающих предметов? И, что даже более важно, как сообщить это местоположение другим?

Что определить абсолютное местоположение невозможно люди поняли очень давно. Можно только относительно чего либо, какого либо ориентира. Пример такого относительного позиционирования можно найти у Конан Дойля в "Обряд дома Месгрейвов". Помните?

"Сколько надо сделать шагов?"
" На север - десять и десять, на восток - пять и пять, на юг - два и
два, на запад - один и один и потом вниз ".

В современной терминологии, ориентир и набор условий, которые определяют его использование, называют системой координат . А сами координаты определяют положение объекта в этой системе .

Развитие мореплавания, астрономии, геометрии, других наук, потребовало более точного и единообразного способа задания координат объектов. Давайте повнимательнее посмотрим на некоторые системы координат, их применение, изменение, и взаимосвязь между ними. В этой статье, как всегда, будет математика, но почти не будет физики.

Одномерная система координат

Давайте вспомним статью " Сага о треугольниках ". Там я немного касался темы систем координат, когда говорил о прямой и плоскости. Начнем с простейшего случая - координатного луча.

Точку, относительно которой указывается положение, или координата, других точек называют началом координат . Обычно ее обозначают "0". Расстояние от начала координат до точки А (в нашем примере) называют координатой . В данном случае координата может быть только положительной, что кажется лишним, и искусственным ограничением. Это можно изменить

Название "координатная прямая" не совсем верное. Прямая не имеет направления. Луч имеет направление, но при этом имеет начало (как в первом случае). Тем не менее, буду использовать именно термин координатная прямая. Но для любителей точности могу сказать, что так как точка делит прямую на два луча, то направление одного из них можно принять за положительное, а другого за отрицательное. Направление положительного луча обозначим стрелкой, а направление отрицательного ничем не будет обозначаться. Точка, разделившая прямую на два координатных луча, относительно которой указывают местоположение (координаты) других точек, точно так же называется началом координат.

В этом примере "координату точки А" можно просто обозначить как "А", и она положительна. Координата точки Б отрицательна и обозначается как "-Б". Расстояние между двумя точками определяется как разность их координат . Исходя из этого получим, для нашего примера, расстояние АБ=А-(-Б)=А+Б.

Несмотря на простоту эта система координат применяется достаточно широко. Посмотрите на обычную линейку. Посмотрите на градусник. И это лишь простейшие примеры того, где она применяется.

Двумерная прямоугольная система координат. Декартова система координат.

Теперь возьмем две пересекающиеся под прямым углом координатные прямые на плоскости. Мы получим самую широко используемую систему координат Декартову прямоугольную систему координат . Ее знают все еще со школьной скамьи. Ее я тоже упоминал, кратко, в статье " Сага о треугольниках ". Давайте посмотрим на нее внимательнее.

Пока все просто, совсем как в школьных учебниках. Теперь координаты точки на плоскости задаются парой чисел. Точка А имеет координаты (Xа,Ya), а точка Б (Хб,-Yб). Координата Х называется абсциссой, а Y ординатой . Расстояние между точками А и Б, или длина отрезка АБ, теперь определяется гораздо сложнее

Откуда взялась эта формула? Если бы отрезок АВ был параллелен оси Х, то его длина была бы равна Хв-Ха, точно так же, как в одномерной системе координат. А если он будет параллелен оси Y, то Yb-Ya. Но у нас отрезок координатным осям не параллелен. А теперь посмотрите на эту же иллюстрацию под несколько другим углом

Видите прямоугольный треугольник? Да, мы опять встретили старого знакомого. И наш отрезок это гипотенуза треугольника. Если вспомнить, что квадрат гипотенузы равен сумме квадратов катетов, то приведенная выше формула становится совершенно очевидной и понятной.

В декартовой системе координат можно задавать не только точки, но и произвольные плоские кривые (мы пока говорим о плоскости). Кривые задаются функциями определяющими зависимость между X и Y. Вот примеры нескольких, хорошо знакомых вам, еще со школы, кривых

Пока ничего особо интересного не было. До сих пор мы не выходили за пределы школьного учебника, но сейчас сделаем небольшой, совсем небольшой, шаг в сторону аналитической геометрии. Не пугайтесь, для понимания будет достаточно знаний геометрии и тригонометрии в рамках школьной программы.

Иногда нужно сменить систему координат, например, для упрощения расчетов. Так координаты вазы на столе можно отсчитывать от угла комнаты, а можно от угла стола. И тут у нас возникает вопрос, а как же изменятся координаты? Другими словами, нам нужны правила преобразования координат между двумя системами координат.

Сначала рассмотрим простейший пример переноса точки начала координат из точки О в точку О1. При этом у нас координатные оси новой системы координат будут параллельны координатным осям старой системы координат

Тут все просто, простейшая арифметика. Мы сдвинули точку начала координат O(0,0) в точку O1(dx,dy). При этом, в новой системе координат точка О1 будет иметь координаты (0,0). Преобразование координат между старой и новой системами будет таким

Но мы можем не только перенести начало координат, но и повернуть новую систему координат .

В этом случае преобразование координат будет сложнее. Я не буду приводить полный вывод формул преобразования координат, что бы излишне не усложнять статью, но покажу, откуда они берутся. Для этого рассмотрим упрощенный случай поворота системы координат без переноса ее начала

Поворот системы координат вокруг своего начала на угол α против часовой стрелки эквивалентен повороту точки А вокруг начала координат на тот же угол, но уже по часовой стрелке. Мы видим два прямоугольных треугольника. Если связать изменение абсциссы и ординаты точки А с углом поворота и добавить сдвиг начала координат, то получим вот такие формулы преобразования

Те, кто знаком с аналитической геометрией, без сомнения, узнали эти формулы. А остальные теперь узнали, откуда они взялись и могут просто применять их, если потребуется.

Давайте вернемся в рамки школьной программы. Кроме замены системы координат возможен и более простой случай преобразования координат. Я говорю об изменении масштаба по осям . По другому это можно назвать деформацией. Масштаб по осям Х и Y может быть разным. При этом точка начала координат остается на месте. Я не буду приводить формулы преобразований, настолько они просты. Все преобразование будет сводиться к умножению, или делению, на коэффициент масштабирования.

Безусловно, возможно и одновременное выполнение переноса центра координат с поворотом и масштабированием.

Двумерные системы координат. Общий случай.

На самом деле, система координат не обязательно требует прямого угла между осями координат . Угол может быть любым. Если при этом оси координат остаются прямыми линиями мы получим аффинную систему координат. Пример аффинной системы можно найти в статье " Сага о треугольниках ", правда там я ее так не называл.

Но координатные оси не обязаны быть прямыми . Возможен, например, такой случай

Рассмотрение подобных систем координат выходит далеко за рамки статьи, поэтому я ограничусь лишь этим примером.

Трехмерная декартова система координат

А если мы перейдем в более привычный нам трехмерный мир? К системе координат добавится ось Z. Теперь у нас Х это ширина, Y это высота, а Z это глубина пространства. Если воспользоваться обычным языком, а не математическим. Координата Z называется аппликатой

При этом с направлением оси Z могут быть варианты. Она может идти от нас, как показано на рисунке, или к нам. Это не меняет саму суть системы, но влияет на знак координаты z. Иногда говорят о правосторонней и левосторонней системах координат . На рисунке я изобразил левостороннюю. Если бы ось Z шла к нам, то система была бы правосторонней.

Точки Ayoz, Axoz и Axoy, на рисунке, являются проекциями точки А на соответствующую координатную плоскость.

С трехмерной декартовой системой координат возможны те же самые преобразования, которые мы рассматривали для двумерной. Но сами формулы будут гораздо сложнее и я не буду их приводить. При желании, их можно найти в учебниках аналитической геометрии.

Полярная система координат

Вы когда-нибудь задумывались о том, насколько противоестественной для человека является декартова система координат? Действительно, эта система фактически "взгляд со стороны", тогда как человек чаще всего чувствует центром именно себя. Вы же не считаете, что, например, дерево расположено от вас в 5 шагах точно направо и 8 шагах точно вперед? Гораздо привычнее сказать, что дерево впереди и немного правее вас и расстояние до него шагов 10.

Этого мало? Посмотрите, например, на свою руку. Она имеет несколько центров вращения - плечо, локоть. И длина костей руки неизменна. Посмотрите на промышленных роботов, например, работающих на сборке автомобиля. Та же самая картина, несколько центров вращения (называемых осями) и сегменты неизменной длины.

Так не проще ли задавать координаты в виде угла поворота относительно центра вращения и расстояния от центра вращения до точки? Пилоты самолетов примерно этим и пользуются. Например, другой самолет на 10 часах и в 100 метрах означает, что он впереди и левее на 60 градусов, а расстояние до него 100 метров.

В математике такая система координат называется полярной. Вместо расстояний по осям в ней задается расстояние от полюса, центра координат, и угол, отсчитываемый против часовой стрелки, от полярной оси.

В полярной системе координаты точки А будут (r,φ). Выглядит непривычно? Между тем, полярная система координат, хоть и менее распространена, чем декартова, среди не математиков, находит широкое применение. При этом надо отметить, что угол φ обычно лежит в пределах от 0 до 180 градусов. Или, что тоже самое, от 0 до π. Если угол больше 180 градусов, то меняют на угол противоположного знака (отсчет не против, а по часовой стрелке).

Уравнениях некоторых кривых в этой системе выглядят проще, чем в декартовой

Да, уравнение окружности, центр которой не расположен в полюсе, выглядит сложноватым. Зато уравнение окружности с центром в полюсе очень простое. А мы ведь всегда можем сменить систему координат перенеся полюс. Прямая линия в полярной системе задается через нормаль, а не двумя точками, но само уравнение достаточно простое.

Кроме механики, я уже говорил о движениях роботов, полярная система находит применение и для работы с комплексными числами. А значит, широко применяется, например, в электротехнике и электронике (помните угол сдвига фазы?). Может использоваться и для векторных вычислений.

Я не буду рассматривать преобразования (сдвиги и вращения) для полярной системы координат. Те, кто в таких преобразованиях нуждаются, аналитическую геометрию и так знают. А для остальных это будет не слишком интересно, Но покажу, как она связана с ранее описанной декартовой системой координат. Да, это опять будут прямоугольные треугольники

Теперь мы можем выразить угол через отношение катетов, то есть координат точки А. А длину вектора r определить через теорему Пифагора. Точно так же легко выполняется и обратное преобразование.

Но давайте посмотрим на эти формулы внимательнее, нет ли тут скрытых проблем? А они есть! Что если наша точка лежит на одной из координатных осей? Увидели? Я специально выделил это красным. Это показывает, что нельзя бездумно применять формулы. Поэтому угол φ обычно вычисляют по другим формулам

В статье приведены формулы вычисления угла в том виде, в каком они приводятся в аналитической геометрии. Однако, в первоначальном варианте я приводил формулы для arcsin и arccos, так как хотел приблизить из вид к "школьному" для упрощения восприятия читателями. Но, как известно, благими намерениями вымощена дорога в ад. И я упустил из виду, что области значений arcsin и arccos не охватывают всего диапазона от 0 до 360 градусов, так как при этом возникает неоднозначность. Таким образом, использование arcsin и arccos требует отдельного учета знака декартовых координат (номера квадранта), что наоборот усложняет их использование. И я не указал этой особенности. Спасибо Трушину Виктору , который заметил эту оплошность в комментариях.

Это не решает проблему полностью, так как остается еще точка лежащая в начале координат. Но это особый случай, так как эта точка является полюсом. Для полюса невозможно указать угол φ, но сам полюс вполне однозначно определяется условием r=0.

Полярная система координат в пространстве

А что насчет полярной системы координат в трех измерениях? А вот тут возможны варианты. Во первых, мы можем провести ось из полюса перпендикулярную нашей плоскости и отсчитывать дополнительную координату по этой оси. Это даст нам цилиндрическую систему координат

Я уже признавался, что художник из меня плохой, поэтому привожу иллюстрацию из учебника аналитической геометрии кафедры математики физического факультета МГУ.

В цилиндрической системе координат координаты точки М будут (ρ,φ,z).

Но мы может указывать дополнительную координату и как угол к этой оси. Что дает нам сферическую систему координат .

В этой системе координат точка М будет иметь координаты (r,φ,Θ).

Обратите внимание, что цилиндрическая и сферическая системы координат различаются лишь способом задания и записи координат. Сами системы определяются идентично - плоскостью, в которой лежит полюс и задается угол φ, и ортогональной это плоскости осью.

Я не буду приводить формулы для преобразования между Декартовой трехмерной системой координат и полярными трехмерными системами координат. Что бы не перегружать и не усложнять статью. Желающие могут найти их в учебниках аналитической геометрии.

Заключение

Пожалуй, на этом я остановлюсь. Я не затронул многие другие системы координат. В астрономии используют топоцентрическую, экваториальные, эклиптическую и галактическую системы координат. Координаты объектов на поверхности земного шара (и глобусе) определяются в географической системе координат. Думаю, все слышали про параллели и меридианы, широту и долготу. Существует геодезическая система координат, учитывающая форму Земли. Есть астрономическая система координат позволяющая определить координаты объектов на поверхности Земли по положению звезд. Этой системой координат пользовались, например, моряки в своих плаваньях к неизвестным берегам.

Эта статья не учебник , это небольшой , и сильно упрощенный , безусловно, далеко не полный , обзор некоторых систем координат использующихся в математике и физике. И рассчитана она не на корифеев математики, а на интересующихся математикой и физикой обычных людей . Для кого то она слишком проста, для кого то слишком сложна. Ее цель заинтересовать .

В геометрии система координат - это система отсчета, в которой числа (или координаты) используются для однозначного определения положения точки или другого геометрического элемента в пространстве. Системы координат позволяют преобразовать геометрические задачи в численные задачи, которые составляют основу аналитической геометрии.

Декартова система координат и полярная система координат - это две общие системы координат, используемые в математике.

Декартовы координаты

Декартовой система использует реальный номер строки в качестве ссылки. В одном измерении числовая прямая простирается от отрицательной бесконечности до положительной бесконечности. Если рассматривать точку 0 как начало, можно измерить длину до каждой точки. Это обеспечивает уникальный способ идентификации позиции в строке с помощью одного номера.

Концепция может быть расширена до двух и трех измерений, где используются числовые линии, перпендикулярные друг другу. Все они имеют ту же точку 0, что и начало. Числовые линии называются осями и часто называются осью X, осью Y и осью Z. Расстояние до точки вдоль каждой оси, начиная с (0, 0, 0), которая также известна как начало координат и задана как кортеж, известна как координата точки. Общая точка в этом пространстве может быть представлена координатой (x, y, z). В системе плоскости, где есть только две оси, координаты задаются как (x, y). Плоскость, созданная осями, известна как декартова плоскость и часто обозначается буквами осей. Например. Плоскость XY.

Эту общую точку можно использовать для описания различных геометрических элементов путем ограничения поведения общей точки определенным образом. Например, уравнение x ^ 2 + y ^ 2 = a ^ 2 представляет собой круг. Вместо того, чтобы рисовать круг с радиусом a, можно обозначить круг более абстрактным способом, показанным выше.

Полярные координаты

Для обозначения точки в полярных координатах используется разностная система отсчета. Система полярных координат использует угол против часовой стрелки от положительного направления оси x и расстояние по прямой до точки в качестве координат.

Полярные координаты могут быть представлены, как указано выше, в двумерной декартовой системе координат.

Преобразование между полярными и декартовыми системами задается следующими соотношениями:

г = √ (х 2 + y 2 ) ↔ x = r cosθ, y = r sinθ

θ = загар -1 (х / у)

В чем разница между декартовыми и полярными координатами?

• В декартовых координатах в качестве осей используются числовые линии, и их можно использовать в одном, двух или трех измерениях. Следовательно, имеет возможность представлять линейную, плоскую и твердую геометрию.

• В полярных координатах в качестве координат используются угол и длина, и они могут представлять только линейную и плоскую геометрию, хотя могут быть преобразованы в цилиндрическую систему координат для представления твердотельных геометрий.

• Обе системы используются для представления мнимых чисел путем определения мнимой оси и играют жизненно важную роль в сложной алгебре. Хотя в простой форме декартовы координаты являются действительными числами (x, y, z), координаты в полярной системе не всегда являются действительными числами; т.е. если угол указан в градусах, координаты не являются действительными; если угол указан в радианах, координаты являются действительными числами.

Читайте также: