Явления природы протекающие по законам степенной функции доклад

Обновлено: 17.06.2024

Объектом исследования в моей статье являются показательная, степенная, тригонометрическая функции, а предметом исследования – свойства этих функций, их применение в природе, науке и технике.

С седьмого класса мы начали изучать понятие функций, их свойства, графики. Однако размеры школьного учебника не позволяют показать всё многообразие задач, требующих для своего решения применение функций. Также в школьном учебнике не излагается история возникновения и развития функции.

Выясним, как развивалось понятие функции, показать полезность изучения функций, доказать взаимосвязь математических и биологических явлений и процессов.

Я поставил перед собой следующие задачи:

1. Выяснить, как зависит вид графика степенной функции от свойств степени.

2. Выяснить, какие законы природы выражаются показательной функцией.

3. Рассказать о применении параболы в науке и технике.

4. Рассказать о процессах органического роста, органического затухания, выравнивания в природе, технике, экономике.

5. Выяснить, какие колебания полезны для человека, какие нет, и с помощью какой функции описываются колебания.

6. Создать тесты в электронном виде для подготовки к Единому Государственному экзамену.

Использованные методы – сбор материала, его анализ и обобщение, создание тестов в электронном виде.

История развития функции

Вавилонские таблички

За две тысячи лет до нашей эры в Двуречье возвышалось царство со столицей в Вавилоне. Жители Двуречья делали плоские плитки из глины и писали на них (еще влажных) заостренной палочкой. Для нас особенно интересны математические плитки – таблички. Вавилоняне умели вычислять длину окружности по ее радиусу, правда, с большой погрешностью; точно вычисляли площадь треугольника, объемы простейших тел. Запас функций у греков был богаче, чем у вавилонян. Но, как бы ни был велик прогресс греческой математики по сравнению с вавилонской, в ней тоже не было ни общего понятия функции, ни обозначений конкретных функций.

Функция Орема

К началу 14-го века в Европе, во Франции жил замечательный математик Никола Орем. Он первым стал изображать график функции. Все величины, по Орему, имеют интенсивности и экстенсивности. Интенсивности находятся в зависимости от экстенсивности. Пусть, например, скорость движения тела зависит от времени. Экстенсивность будем откладывать на горизонтальной прямой от точки А. Отрезок АС, длина которого равна экстенсивности, называется долготой. В точке С проведем перпендикуляр к АВ и отложим на нем отрезок CD, длина которого равна интенсивности. Отрезок CD Орем называет широтой. Если такое построение произвести для каждой точки отрезка АВ, то получим линию EDF, которую Орем называет линией верхнего края или линией интенсивностей.

Замечательные работы Орема были известны широко, однако они мало повлияли на развитие математики.

Функция Лейбница

Одним из создателей новой математики был великий немецкий ученый Готфрид Вильгельм Лейбниц. Именно Лейбниц ввел в математику слово “функция” (от латинского “functio”- исполнение обязанностей, деятельность).

Функциями Лейбниц называл “всякие части прямых линий, которые получают, проводя бесчисленные прямые, соответствующие неподвижной точке и точкам кривой”.

Вот один из примеров такой “функции”, который приводит сам Лейбниц.

Дана кривая l и прямая MN. Возьмем на кривой l точку С и проведем касательную к кривой l в этой точке. Обозначим через Т точку пересечения прямой MN с касательной. Отрезок СТ и есть “функция” по Лейбницу. Этот отрезок меняется, когда точка С движется по кривой l.

Таким образом, в термин “функция” Лейбниц вкладывал смысл, отличный от нашего. Можно сказать, что у Лейбница было предчувствие понятия функции. Таким образом, имя “функция” уже появилось на свет в 1694 году, но современного смысла оно еще не имело.

Эйлер же ввел для функции обозначение f(x), которое используется и сейчас.

Показательная функция

Графики этой функции. Показательная функция очень часто реализуется в физических, биологических и иных законах. В жизни нередко приходится встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид у=у0аx.

По закону показательной функции размножалось бы все живое на Земле, если бы для этого были благоприятные условия. Доказательство тому – распространение в Австралии кроликов, которых там раньше не было. Одна пара кроликов дает за год приплод в 50 крольчат. Если бы все они оставались в живых, то в грубом приближении можно было бы считать, что число кроликов увеличивается в 25 раз каждый год. Но тогда через два года их число увеличивается в 625 раз, через 3 года в 15 625 раз и т. д. , уже через 5 лет было бы 255. Разумеется, в действительности мы не наблюдаем такого чудовищного роста.

В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т. е. по закону показательной функции. Эти процессы называются процессами органического роста или органического затухания.

Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в банке, восстановление гемоглобина в крови донора или раненого. Закон органического роста выражается формулой: N = Nоekt. В природе и технике часто можно наблюдать процессы, которые подчиняются законам выравнивания, описываемым показательной функцией.

Например, если снять кипящий чайник с огня, то сначала он остывает быстро, а потом остывание идет гораздо медленнее. Скорость остывания пропорциональна разности между температурой Т чайника и температурой То окружающего воздуха. Постепенно происходит теплообмен между чайником и воздухом и температура выравнивается. Закон изменения температуры чайника имеет вид:

Т = Тo + (100 –Тo) е-kt.

Описание радиоактивного распада так же связано с показательной функцией. Количество распадающегося за единицу времени вещества всегда пропорционально имевшемуся количеству вещества. Радий распадается в зависимости от времени по закону М = Мое-kt, где: Мо – начальное количество радия, k – некоторый коэффициент.

В конце 20-х годов Н. Н. Семенов описал теорию цепных реакций. Было установлено, что при попадании нейтрона в атомное ядро урана оно раскалывается, причем этот процесс сопровождается испусканием новых нейтронов. Ученые научились управлять процессом размножения нейтронов при помощи знаний о показательной функции.

Степенная функция

Функция y = xp, где р – действительное число. Свойства и график степенной функции существенно зависят от свойств степени.

График функции y = x2n имеет такой же вид, как, например график функции y = x4.

График функции y = x2n-1 имеет такой же вид, как, например, график функции y = x3.

График функции y = 1/x2n имеет такой же вид, как, например, график функции y = 1/x2.

График функции y = 1/x2n-1 имееттакой же вид, как, например, график функции y = 1/x3.

График функции у = хр имеет такой же вид, как например, график функции у = х 1/3 (при 0 1), или как график функции у = х4/3 (при р > 1 ). График функции у = хр , где р – отрицательное число, имеет такой же вид, как например, график функции у = х –1/3.

Замечательное свойство параболы широко используется в науке и технике. Известно также, что многие законы природы выражаются в виде квадратичной зависимости. Например, скорость воды в реке на разных глубинах разная: у дна и у поверхности наименьшая, где-то внутри потока она наибольшая. Можно считать, что если от оси Oy отложить горизонтальные отрезки, равные по длине скорости воды на соответствующей глубине, то получится парабола с горизонтальной осью, вершина которой находится на 1/3 глубины потока.

Представим себе, что очень узкая зеркальная полоска изогнута в форме дуги параболы.

Это свойство параболических зеркал используют при конструировании солнечных печей, солнечных электростанций, отражательных телескопов- рефлекторов.

Тригонометрическая функция

Различные колебания окружают нас на каждом шагу. Механические колебания применяются для просеивания материалов на виброситах, безболезненного высверливания отверстий в зубах. Акустические колебания нужны для приема и воспроизведения звука, а электромагнитные – для радио, телевидения, связи с космическими ракетами. С помощью электромагнитных колебаний учеными были получены снимки обратной стороны Луны и вечно закрытой облаками Венеры. Колебания сопровождают и биологические процессы, например, слух, зрение, работу сердца и мозга.

Но колебания не всегда полезны. Вибрация станка может привести к браку; вибрация самолетных крыльев при неблагоприятных условиях может привести к катастрофе. Если колебания под контролем человека полезны, то, вырвавшись из-под этого контроля, они превращаются в опасного врага. Надо уметь изучать колебания, знать их свойства.

Самый удобный математический метод для описания колебаний в применении тригонометрических функций.

График функции y = sin x называется синусоида.

Почему летом теплее, чем зимой? Дело в наклоне земной оси по отношению к плоскости земной орбиты. Зимой в умеренных широтах солнце невысоко поднимается над горизонтом, его лучи лишь скользят по Земле. Летом в моменты наивысшего подъема над горизонтом солнце приближается к зениту, его лучи падают почти отвесно на те же участки Земного шара. В зависимости от наклона солнечных лучей она по-разному распределяется по земной поверхности. Больше всего ее приходится на участок поверхности при отвесном падении света. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок.

Какая доля солнечной энергии приходится на участок земли при наклонном падении лучей под тем или иным углом? Проследим эволюцию жирно очерченного прямоугольного треугольника на приведенных чертежах. Очевидно, интересующая нас доля солнечной энергии равна отношению указанного катета к гипотенузе. Число, определенное таким образом и поставленное в соответствие углу, для которого оно определялось, называется синусом этого угла.

Это есть синусоида. Если что-то и кажется здесь непривычным, так это малая протяженность кривой: обычно ее рисуют безгранично разбегающейся вдоль оси абсцисс.

Я проанализировал и изучил литературу по истории развития функции, применении её в науке и технике: в измерении скорости воды в реке на разных глубинах, свойство параболических зеркал при конструировании солнечных печей, солнечных электростанций, телескопов – рефлекторов, фар, прожекторов; свойство тригонометрической функции при расчёте количества солнечной энергии на поверхность земли в зависимости от угла падения солнечных лучей; по закону показательной функции описаны процессы органического роста или органического затухания, также ей подчинены законы выравнивания. Мною были исследованы данные функции.

1. Жизненные процессы описывающиеся показательной функцией

2. Применение показательной функции в природе и технике:

ПРИМЕНЕНИЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ В
ПРИРОДЕ И ТЕХНИКЕ:
Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он
быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что
скорость остывания пропорциональна разности между температурой чайника
и температурой окружающей среды. Чем меньше становится эта разность,
тем медленнее остывает чайник. Если сначала температура чайника равнялась
Т0, а температура воздуха T1, то через t секунд температура Т чайника
выразится формулой:
T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан,
и количества воды, которое в нем находится.

3. При падении тел в безвоздушном пространстве скорость их непрерывно возрастает.

ПРИ ПАДЕНИИ ТЕЛ В БЕЗВОЗДУШНОМ ПРОСТРАНСТВЕ
СКОРОСТЬ ИХ НЕПРЕРЫВНО ВОЗРАСТАЕТ.
При падении тел в воздухе скорость падения тоже
увеличивается, но не может превзойти определенной
величины. Если считать, что сила сопротивления воздуха
пропорциональна скорости падения парашютиста, т.е. что
F=kv , то через t секунд скорость падения будет равна:
v=mg/k(1-e-kt/m), где m - масса парашютиста.

4. В биологии тоже есть примеры показательной функции:

В БИОЛОГИИ ТОЖЕ ЕСТЬ ПРИМЕРЫ
ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ:
Закон органического размножения: при
благоприятных условиях (отсутствие
врагов, большое количество пищи)
живые организмы размножались бы по
закону показательной функции.
Например: одна комнатная муха может за
лето произвести 8 *1014 особей
потомства. Их вес составил бы несколько
миллионов тонн (а вес потомство пары
мух превысил бы вес нашей планеты), они бы
заняли огромное пространство, а если
выстроить их в цепочку, то её длинна будет
больше, чем расстояние от Земли до Солнца.
Но так как, кроме мух существует множество
других животных и растений, многие из
которых являются естественными врагами мух
их количество не достигает вышеуказанных
значений.

Рост народонаселения. Изменение
числа людей в стране на небольшом
отрезке времени описывается
формулой
, где N0 - число
людей в момент времени t=0,
N -число людей в момент
времени t, a-константа.

6. В физике тоже есть величины и законы подчиненные показательной функции:

В ФИЗИКЕ ТОЖЕ ЕСТЬ ВЕЛИЧИНЫ И ЗАКОНЫ
ПОДЧИНЕННЫЕ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ:
Также широко применяется показательная
функция при описании процессов ядерной физики
m = m0(1/2)-t/t0 , где m0 - первоначальная масса
вещества
В ядерных реакциях: скорость разветвлённо-цепного
процесса в
газовой фазе в начальных стадиях (вплоть до
выгорания 30-40% газа) выражается формулой:

Также, при прохождении света через мутную
среду, каждый её слой поглощает строго
определенную часть падающего на него света.
I = I0e-ks , где s – толщина слоя,
k – коэффициент характеризующий мутную среду.

8. Показательная функция является неотъемлемой частью нашей жизни, а также играет очень важную роль в различных сферах

ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ ЯВЛЯЕТСЯ
НЕОТЪЕМЛЕМОЙ
ЧАСТЬЮ
НАШЕЙ
ЖИЗНИ, А ТАКЖЕ ИГРАЕТ ОЧЕНЬ
ВАЖНУЮ РОЛЬ В РАЗЛИЧНЫХ СФЕРАХ
ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА.

Автор работы награжден дипломом победителя III степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Целью моей работы является исследование сфер применения показательной функции.

Объект исследования: показательная функция.

Показательная функция часто применяется в физике, химии, биологии, географии, экономике и иных науках.

Рост количества бактерий, концентрация адреналина в крови, способность почек выводить из крови радиоактивные изотопы, восстановление концентрации гемоглобина в крови, рост количества древесины, количество радиоактивного вещества, изменение количества населения – все это измеряется по законам показательной функции.

В жизни нередко приходиться встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине. В этом случает рассматриваемая величина будет изменяться по закону, имеющему вид y=y0ax

Практическая значимость работы заключается в том, что она позволяет объективно оценить значимость показательной функции, основываясь на рассмотренных фактах, раскрывая особенности применения показательной функции в современной жизни человека.

Материал исследовательской работы может быть использован в форме презентации для выступления различных публичных мероприятиях, в школе; для публикации в печатных изданиях (в научно-популярной литературе), размещения данных о проекте на сайте нашей школы и других сайтах определенной тематики.

Подбор, изучение, анализ информации о функциях, в частности, показательной функции.

Анкетирование с целью узнать, насколько люди осведомлены о сфере применения показательной функции.

Исследование свойств показательной функции.

Примеры применения показательной функции.

Задачи на показательную функцию.

Доказать, что функциональные зависимости существуют во всех сферах жизни;

Расширить знания о показательной функции и методах решения уравнений;

Узнать, какие явления из жизни и некоторых наук описывает показательная функция;

Научиться применять полученные знания в нестандартных ситуациях на основе рассмотрения примеров из реальной жизни, при решении практико-ориентированных задач.

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет (1540-1603) и Рене Декарт (1596-1650);

Они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.

3.1 Аналитическое определение функции.

Готфрид Вильгельм Лейбниц (1646-1716)

Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье.

Из трудов Фурье следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением.

Жан Батист Жозеф Фурье4.1 Примеры применения показательной функции

Так утверждал великий ученый, математик Леонард Эйлер. И он был в корне прав, говоря о том, что показательная функция применятся во многих сферах жизни человека.

Кроме того, перед началом исследования, мною был проведен опрос с целью узнать, осведомлены ли люди о том, что такое показательная функция и где она применяется:

В итоге, 72% опрошенных не знают, где применяется данная функция. Но в своем исследовании я решила рассказать, где же используется данная функция.

Приведем примеры, где мы сталкиваемся с показательной функцией в повседневной жизни, а также как она применяется на практике.

Напомним вид показательной функции: у=а х , где а>0, а≠1, x Є R. Показательная функция встречается в самых различных областях науки - в физике, химии, биологии, экономике.

A-изменение количества древесины во времени; A₀-начальное количество древесины; t-время; k, а - некоторые постоянные.

2. Давление воздуха убывает с высотой по закону P=P₀*a -kh , где P- давление на высоте h, P₀ - давление на уровне моря, а- некоторая постоянная.

Процессы выравнивания (именно так называют процессы, изменяющиеся по законам показательной функции) часто встречаются и в биологии.

3. Рост количества бактерийпроисходит по закону N=5 t , где N-число колоний бактерий в момент времени t;

Это закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции.

Также вспомним что, при испуге в кровь внезапно выделяется адреналин, который потом разрушается, причем скорость разрушения примерно пропорциональна количеству этого вещества, еще остающемуся в крови. При диагностике почечных болезней часто определяют способность почек выводить из крови радиоактивные изотопы, причем их количество в крови падает по показательному закону.

Примером обратного процесса может служить восстановление концентрации гемоглобина в крови у донора или у раненого, потерявшего много крови. В этом случае по показательному закону убывает разность между нормальным содержанием гемоглобина и имеющимся количеством этого вещества.

4. Количество радиоактивного вещества, оставшегося к моменту t,

описывается формулой , где No – первоначальное количество вещества,

T_1/2– период полураспада.

5. Площадь сечения троса связана с сопротивлением разрыва также по показательному закону.

Сейчас многие моря и океаны бороздят исследовательские корабли. В заранее установленных местах они останавливаются и спускают за борт трос, на конце которого находятся приборы. Их опускают на дно, а потом поднимают наверх и записывают показания. Но иногда происходит печальное событие — трос разрывается и все ценные приборы оказываются погребенными на дне моря.

Казалось бы, этой беды можно было бы избежать, сделав трос потолще. Но тут возникает новое осложнение — верхние части троса должны удерживать не только спускаемые приборы, но и нижнюю часть самого троса, а потому при утолщении всего троса на верхнюю часть ляжет слишком большая нагрузка.

Поэтому целесообразно делать нижнюю часть троса тоньше, чем верхнюю. Возникает вопрос: как должна меняться толщина троса для того, чтобы в любом его сечении на 1 см2 приходилась одна и та же нагрузка?

Исследование этого вопроса показало, что площадь сечения троса должна изменяться по следующему закону: , где

So — площадь его нижнего сечения,

S — площадь сечения на высоте х от нижнего сечения,

γ — удельный вес материала, из которого сделан трос,

Р — вес в воде опускаемого груза (нам пришлось написать в формуле γ — 1 вместо γ, так как и материал троса теряет в воде вес по закону Архимеда).

Такой трос называют тросом равного сопротивления разрыву.

6. Процесс изменения температуры чайника при кипении выражается формулой:

Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)e-kt+T1,где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.

7. При падении тел в безвоздушном пространстве скорость их непрерывно возрастает. При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определённой величины.

8. При прохождении света через мутную среду каждый слой этой среды поглощает строго определенную часть падающего на него света. Сила света I определяется по формуле: I = I₀e -ks , где

s – толщина слоя;

k – коэффициент, характеризующий мутную среду

В ходе проведения исследований данного материала, анализа информации, моя гипотеза о том, что функциональные зависимости существуют во всех сферах жизни, подтверждена.

Также мы расширили знания о показательной функции, изучили свойства показательной функции, узнали многое об истории развития понятия функции.

Показательная функция обладает следующими свойствами:
Д(у): множество R всех действительных чисел; Е(у):множество всех положительных чисел; Показательная функция у=ах является возрастающей на множестве всех действительных чисел,если а>1,и убывающей,если 0 1 ,то функция выпукла вниз.

Слайд 6

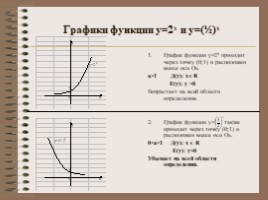
Графики функции у=2х и у=(½)х
График функции у=2х проходит через точку (0;1) и расположен выше оси Ох. а>1 Д(у): х є R Е(у): у >0 Возрастает на всей области определения. График функции у= также проходит через точку (0;1) и расположен выше оси Ох. 0 0 Убывает на всей области определения.

Слайд 7

Слайд 8

Наглядный бытовой пример!
Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась Т0, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)ekt+T1 где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.

Слайд 9

При падении тел в безвоздушном пространстве скорость их непрерывно возрастает
При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определенной величины

Слайд 10

Рассмотрим задачу о падении парашютиста. Если считать, что сила сопротивления воздуха пропорциональна скорости падения парашютиста, т.е. что F=kv , то через t секунд скорость падения будет равна: k(1-e ) где m - масса парашютиста. Через некоторый промежуток времени е станет очень маленьким числом, и падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта. Данная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т.д.
mg
V=
кt m
кt m

Слайд 11

Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.

Слайд 12

Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива определиться формулой: M=m(ev/v0-1) Например, для того чтобы ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива.
Формула К.Э.Циалковского

Слайд 13

Применение в ядерной физике
Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время остается половина первоначального количества вещества. Этот промежуток времени t0 называется периодом полураспада. Вообще через t лет масса m вещества будет равна: m=m0(1/2)t/t0, где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.

Слайд 14

Слайд 15

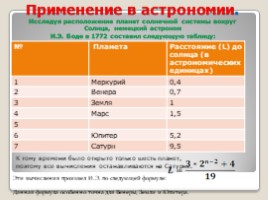
Применение в астрономии. Исследуя расположение планет солнечной системы вокруг Солнца, немецкий астроном И.Э. Боде в 1772 составил следующую таблицу:
№ Планета Расстояние (L) до солнца (в астрономических единицах)
1 Меркурий 0,4
2 Венера 0,7
3 Земля 1
4 Марс 1,5
5
6 Юпитер 5,2
7 Сатурн 9,5
К тому времени было открыто только шесть планет, поэтому все вычисления останавливаются на Сатурне.
Эти вычисления произвел И.Э. по следующей формуле: Данная формула особенно точна для Венеры, Земли и Юпитера.

Слайд 16

Как известно, между Марсом и Юпитером планеты не существует, но если следовать таблице Боде, на данной орбите должно находиться какое-либо космическое тело. И действительно, после некоторых исследований учёными был открыт пояс астероидов. Это было воистину торжеством науки и триумфом математики!

Слайд 17

Слайд 18

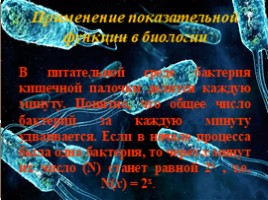
Применение показательной функции в биологии
В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно, что общее число бактерий за каждую минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е. N(х) = 2х.

Слайд 19

Применение в биологии
Процессы выравнивания (именно так называют процессы, изменяющиеся по законам показательной функции) часто встречаются и в биологии. Например, при испуге в кровь внезапно выделяется адреналин, который потом разрушается, причем скорость разрушения примерно пропорциональна количеству этого вещества, еще остающемуся в крови. При диагностике почечных болезней часто определяют способность почек выводить из крови радиоактивные изотопы, причем их количество в крови падает по показательному закону. Примером обратного процесса может служить восстановление концентрации гемоглобина в крови у донора или у раненого, потерявшего много крови. В этом случае по показательному закону убывает разность между нормальным содержанием гемоглобина и имеющимся количеством этого вещества. Как и при радиоактивном распаде, скорость распада или восстановления измеряется временем, в течение которого распадается (соответственно восстанавливается) половина вещества. Для адреналина этот период измеряется долями секунды, для веществ, выводимых почками, — минутами, а для гемоглобина — днями.

Слайд 20

По такому же принципу распространились завезённые в Австралию кролики, которые стали экологической катастрофой для этого уникального региона. Рост различных видов микроорганизмов и бактерий, дрожжей, ферментов все эти процессы подчиняются одному закону: N = N0ekt
Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции. Например: одна комнатная муха может за лето произвести 8 1014 особей потомства. Их вес составил бы несколько миллионов тонн (а вес потомство пары мух превысил бы вес нашей планеты), они бы заняли огромное пространство, а если выстроить их в цепочку, то её длинна будет больше, чем расстояние от Земли до Солнца. Но так как, кроме мух существует множество других животных и растений, многие из которых являются естественными врагами мух их количество не достигает вышеуказанных значений.
Применение в биологии.

Читайте также: