Устойчивость сжатых стержней доклад

Обновлено: 02.07.2024

Понятие о потере устойчивости сжатого стержня. Сила, при которой происходит снижение устойчивости центрально стержня. Критическая сила при его продольном изгибе. Формула Эйлера. Устойчивость стержней различной гибкости. Местные напряжения и их виды.

Рубрика	Физика и энергетика
Вид	реферат
Язык	русский
Дата добавления	18.03.2018
Размер файла	730,3 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Устойчивость сжатых стержней

1. Понятие о потере устойчивости сжатого стержня

Деформированное (напряженное) состояние сжатия возникает в некоторых звеньях стержневых механизмов. В основном - это шатуны шарнирных и ползунных механизмов, используемых в качестве исполнительных механизмов механических прессов, поршневых компрессоров, поршневых двигателей и пр.

При сжатии стержень может находиться в одном их двух состояний: устойчивом и неустойчивом. Напомним, что устойчивость - это способность конструкции или звена (в данном случае - стержня) сохранять первоначальную форму упругого равновесия под действием внешних сил.

Когда сжатый вдоль оси стержень находится в устойчивом состоянии, то небольшая боковая нагрузка вызовет его упругую деформацию. А именно, под действием этой нагрузки стержень незначительно изогнется, то есть, отклонится от первоначального положения равновесия, но после снятия боковой нагрузки он распрямится, то есть, возвратится в исходное положение равновесия.

Если сила, сжимающая стержень вдоль оси, будет увеличиваться, то при некотором ее значении прямолинейная форма равновесия становиться неустойчивой. В этом случае, даже малая боковая нагрузка приводит к внезапному изгибу, а после снятия этой нагрузки стержень не возвращается в первоначальное прямолинейное положение. Такое явление внезапного изгиба центрально сжатого стержня называется потерей устойчивости или продольным изгибом. Потеря устойчивости опасна тем, что при дальнейшем даже небольшом увеличении продольной силы прогиб стержня быстро увеличивается, и это может привести к его разрушению.

Наименьшая сила, при которой происходит потеря устойчивости центрально сжатого стержня, называется критической силой F_кр. Таким образом, центральная сила, значение которой больше критического, приводит к продольному изгибу стержня (рис. 16.1).

а) ось стержня не является абсолютно прямолинейной, она имеет небольшую начальную кривизну, например, как следствие неточности изготовления, термообработки и пр.;

б) вектор сжимающей силы не проходит точно по оси стержня, а смещен относительно нее на некоторую величину вследствие тех же причин.

Эти обстоятельства приводят к возникновению изгибающего момента, смоделированного в предыдущих рассуждениях поперечной силой.

Заметим, что продольный изгиб стержня - не единственный случай потери устойчивости первоначальной формы равновесия; при определенных условиях потеря устойчивости может наступить в кольцах, тонкостенных оболочках, балках и пр.

2. Критическая сила при продольном изгибе

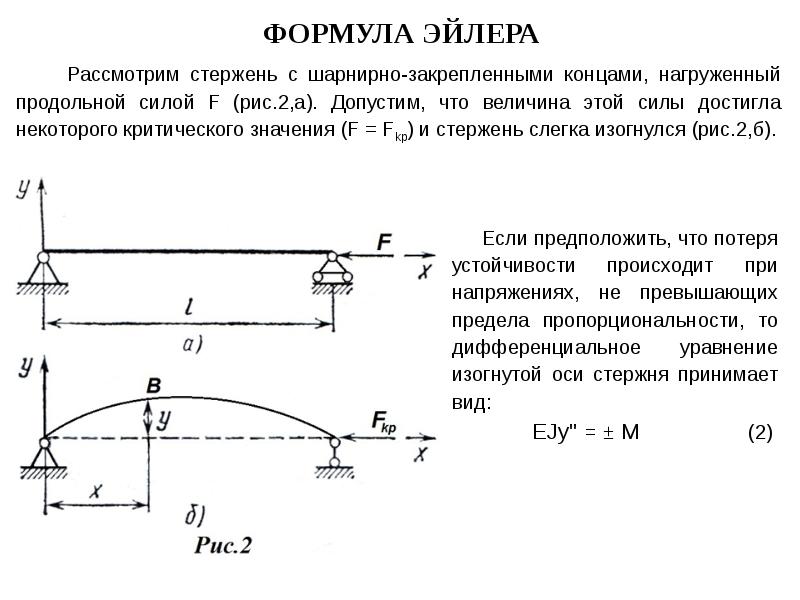
Явление продольного изгиба было исследовано в середине 19 века Эйлером (этот русский ученый немецкого происхождения уже упоминался в §5.2 по зубчатым механизмам). В решении Эйлера предполагалось, что изгиб стержня, сжатого осевой силой, происходит в пределах упругих деформаций (в пределах справедливости закона Гука), то есть напряжение в стержне не может превышать предела пропорциональности для его материала. На основании исследования им была предложена формула (формула Эйлера), позволяющая определить величину критической силы F_крдля центрально сжатого стержня. Приведем эту формулу без вывода:

где: Е - модуль продольной упругости материала стержня в МПа;

J_min - наименьший из осевых моментов инерции поперечного сечения стержня в мм 4 (потеря устойчивости стержня происходит в плоскости наименьшей жесткости);

l - длина стержня в мм;

- коэффициент приведения длины, учитывающий характер закрепления концов стержня.

Произведение lчасто называют приведенной длиной стержня. На рис. 16.2 приведены примеры наиболее часто встречающихся способов закрепления стержней и даны соответствующие им значения коэффициентов . Тонкими линиями показаны возможные формы оси стержня при продольном изгибе.

Под действием критической силы в поперечных сечениях стержня возникают нормальные напряжения, которые также являются критическими _кр. С учетом (16.1) имеем:

где S - площадь поперечного сечения стержня.

Для преобразования этого выражения используем радиус инерции сечения относительно оси (14.8) - квадрат радиуса инерции равен отношению осевого момента инерции сечения к его площади:

Тогда из (16.2) имеем:

Из формулы (16.4) видно, что гибкость полностью определяет величину критического напряжения для стержня из данного материала. Чем больше , тем меньше _кр и тем меньше величина критической силы, вызывающей продольный изгиб стержня. И наоборот - чем меньше гибкость стержня, тем больше величина критического напряжения, однако, она не может превышать предела пропорциональности _П (см. выше). Таким образом, должно соблюдаться условие:

Знак равенства в этом выражении определяет наименьшее (предельное) значение гибкости _пред, при котором формула Эйлера еще применима:

Приведем значения предельной гибкости для некоторых металлов. Для стали марки Ст 3 _П = 200 МПа, Е = 210 5 МПа; тогда:

Для стали марки Ст 5 _пред 90, для чугуна _пред 80.

Если гибкость стержня меньше предельного значения, то пользоваться формулой Эйлера нельзя, так как в этом случае получается завышенное (недопустимое) значение критической силы.

3. Устойчивость стержней различной гибкости

Так как формула Эйлера справедлива только для стержней определенной гибкости, то возникает общий вопрос о классификации стержней по их гибкости. В этой связи различают три вида стержней: стержни большой гибкости, стержни средней гибкости и стержни малой гибкости. Причем значение гибкости для металлических стержней может колебаться в пределах 0 5 Н/мм 2 (МПа). Коэффициент Пуассона для стали м₁ = м₂ = 0,3. Подставляя эти значения и формулу (17.5) в выражение (17.3) после извлечения числовых значений из-под корня, получим:

Эта формула справедлива для любых стальных цилиндров с постоянными или переменными радиусами кривизны, в том числе для цилиндров с образующими в виде эвольвент, то есть, для поверхностей зубьев. В этом случае, r₁ и r₂ - радиусы кривизны эвольвент зубьев в точке контакта. Знак минус в формулах (17.3) и (17.5) относится к случаю внутреннего контакта, когда поверхность одного из цилиндров вогнутая (контакт роликов с внешним кольцом подшипника, внутреннее зубчатое зацепление и пр.).

Формула (17.6) показывает, что контактные напряжения не пропорциональны нагрузке, например, если нагрузка увеличится в четыре раза, то контактные напряжения возрастут в два раза. То есть, контактные напряжения увеличиваются медленнее, чем нагрузка. Это объясняется тем, что с увеличением нагрузки увеличивается и площадка контакта. Если площадка контакта увеличится настолько, что станет сопоставимой с радиусами кривизны контактирующих тел, то приведенные выше расчетные зависимости оказываются непригодными для нахождения напряжений в контакте.

В частности, такой случай имеет место при внутреннем контакте цилиндров, диаметры которых мало отличаются друг от друга (рис. 17.4а). Примерами такого контакта могут служить низшие кинематические пары плоских механизмов: вал в подшипнике скольжения, шарниры стержневых механизмов, шарниры цепей цепных передач. Разность диаметров здесь минимальна и объясняется необходимостью относительного движения в присутствии смазки. Другим примером является соединение деталей при помощи чистого болта или штифтовое соединение. Разность диаметров в этом случае измеряется сотыми долями миллиметра и объясняется технологическими соображениями сборки или эксплуатации соединения.

Напряжения при таком контакте уже фактически не являются местными, так как распределены по относительно большой поверхности. Если их и называют иногда местными, то лишь условно, чтобы отличить от других напряжений - растяжения, изгиба или кручения, распределенных равномерно по всему объему деталей.

Контактные напряжения в этих случаях ограничены допустимым удельным давлением в подшипниках и шарнирах или допустимым напряжением смятия между телом болта или штифта и цилиндрической поверхностью отверстия в детали. Действительное распределение напряжений по цилиндрическим контактирующим поверхностям довольно сложно, поэтому расчет ведется условно по напряжению в диаметральной плоскости шарнира или болта (штифта).

Условие прочности на смятие для штифтового соединения, нагруженного растягивающими силами (рис. 17.4б), выглядит так:

где: S_см - площадь смятия;

- толщина наиболее тонкой соединяемой детали;

d - диаметр штифта;

[_см] - допускаемое напряжение смятия.

Допускаемое напряжение смятия обычно принимается в два, два с половиной раза больше допускаемого напряжения на растяжения для материала штифта или наиболее тонкой из соединяемых деталей:

3. Артоболевский И.И. Механизмы в современной технике. Том III. Зуб¬чатые механизмы. М., Наука, 1973.

4. Артоболевский И.И. Теория механизмов и машин. М., Наука, 1975.

6. Гавриленко Б.А. и др. Гидравлический привод. М., Машиностроение, 1968.

9. Коловский М.З. Динамика машин. Л., Ленинградский политехнический институт, 1980.

10. Основы расчета и конструирования деталей летательных аппаратов. Под ред. Кестельмана В.Н. Москва, 1989.

11. Пневмопривод систем управления летательных аппаратов. Под ред. Чашина В.А. М., Машиностроение, 1987.

13. Пятаев А.В. Теория механизмов и машин. Учебное пособие. Ташкент, Ташкентский государственный авиационный институт, 2001.

14. Пятаев А.В. Динамика машин. Ташкентский политехнический институт. Ташкент, 1990.

15. Пятаев А.В. Детали машин. Учебное пособие. Ташкент, Ташкентский государственный авиационный институт, 2004.

16. Справочник машиностроителя, том 3. Под редак¬циейАчеркана Н.С. Москва, Машгиз, 1963.

17. Справочник машиностроителя, том 4, книги I и II. Под редак¬циейАчеркана Н.С. Москва, Машгиз, 1963.

18. Теория механизмов и машин. Под ред. Фролова К.В. М., Высшая школа, 1987.

19. Тимошенко С.П. Колебания в инженерном деле. М., Физматгиз, 1959.

Подобные документы

Понятие равновесного состояния, его виды. Пределы применимости формулы Эйлера. Влияние условий закрепления концов стержня на величину критической силы. Понятие коэффициента запаса на устойчивость. Энергетический способ определения критических сил.

курс лекций [888,8 K], добавлен 23.04.2009

Равновесное состояние упругой системы называется устойчивым, если оно мало изменяется при малых возмущениях. Явление потери устойчивости. Определение величины критической силы для стержня, теряющего устойчивость в упругой стадии, по формуле Эйлера.

реферат [37,6 K], добавлен 08.01.2009

Определение нормальных напряжений в произвольной точке поперечного сечения балки при косом и пространственном изгибе. Деформация внецентренного сжатия и растяжения. Расчет массивных стержней, для которых можно не учитывать искривление оси стержня.

презентация [156,2 K], добавлен 13.11.2013

Расчет электромеханических переходных процессов в системе электропередачи. Предельное снижение напряжения на шинах асинхронного двигателя. Оценка статической и динамической устойчивости системы. Аварийный и послеаварийный режимы при коротком замыкании.

курсовая работа [1,2 M], добавлен 10.12.2014

Понятие растяжения как вида нагружения, особенности действия сил и основные характеристики. Различия между сжатием и растяжением. Сущность напряжения, возникающего в поперечном сечении растянутого стержня, понятие относительного удлинения стержня.

реферат [857,3 K], добавлен 23.06.2010

Гипотезы сопротивления материалов, схематизация сил. Эпюры внутренних силовых факторов, особенности. Три типа задач сопротивления материалов. Деформированное состояние в точке тела. Расчёт на прочность бруса с ломаной осью. Устойчивость сжатых стержней.

курс лекций [4,1 M], добавлен 04.05.2012

Понятие устойчивости применительно к электрической системе. Определение взаимных и собственных проводимостей при различных системах возбуждения, определение коэффициента запаса статической устойчивости. Расчёт динамической устойчивости данной системы.

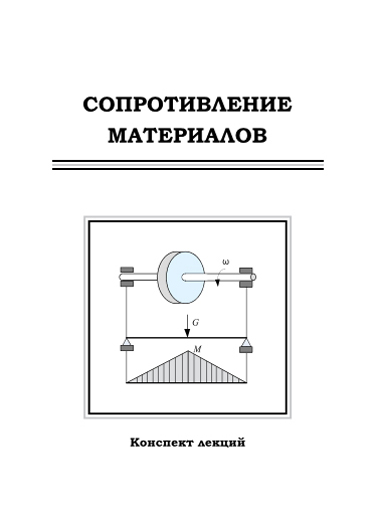
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсильно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.

Рис. 37. Потеря устойчивости

Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.

Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:

Устойчивость сжатого стержня. Задача Эйлера.

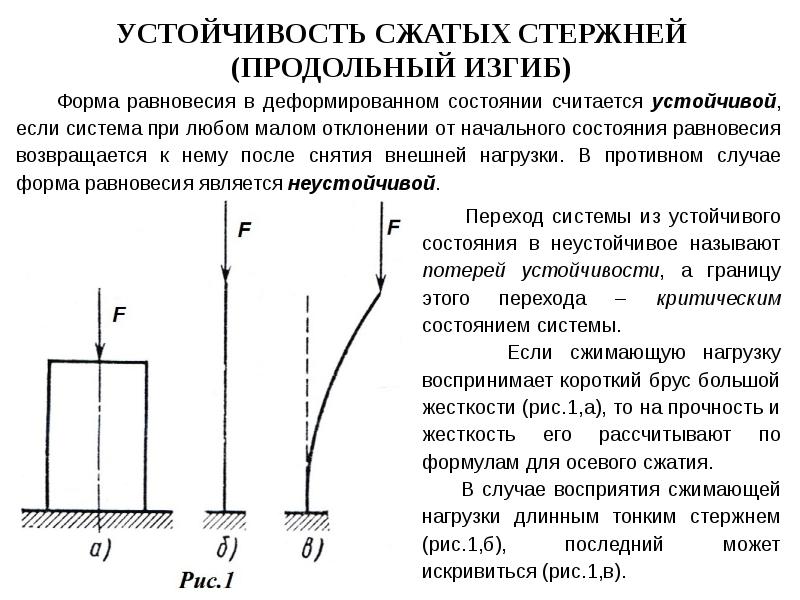
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.

Рис. 38. Сжатый стержень

Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:

где y – прогиб стержня в произвольном сечении с координатой x.

Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

(26)

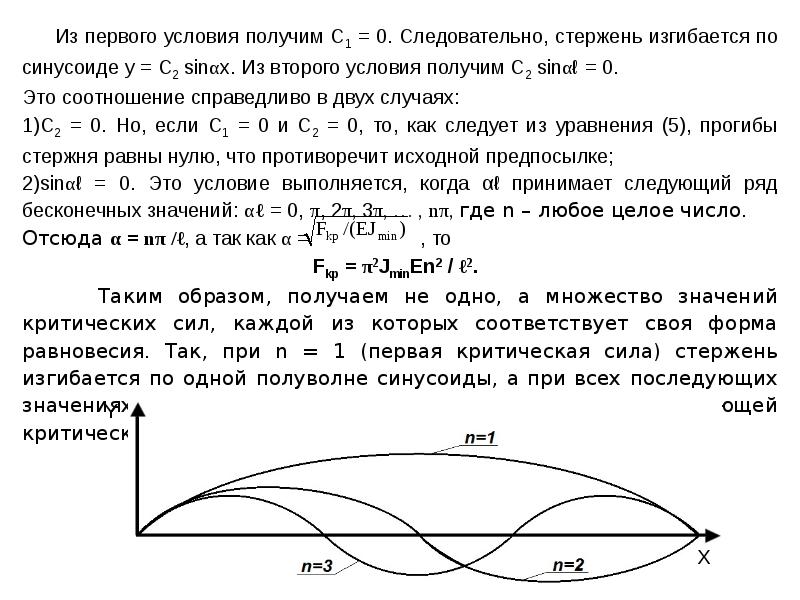
Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

(27)

Это выражение – формула Эйлера.

Зависимость критической силы от условий закрепления стержня.

Формула Эйлера была получена для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.

Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.

Рис. 39. Различные случаи закрепления стержня

Общая формула Эйлера:

(28)

где μ·l = l_пр – приведенная длина стержня; l – фактическая длина стержня; μ – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)

Таким образом, окончательно условие устойчивости примет вид

(29)

Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.

Проверочный расчет

Порядок проверочного расчета на устойчивость выглядит так:

– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;

– по справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;

– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.

Проектировочный расчет

При проектировочном расчете (подобрать сечение под заданную нагрузку) в расчетной формуле имеются две неизвестные величины – искомая площадь поперечного сечения A и неизвестный коэффициент φ (так как φ зависит от гибкости стержня, а значит и от неизвестной площади A). Поэтому при подборе сечения обычно приходится пользоваться методом последовательных приближений:

– обычно в первой попытке принимают φ₁ = 0,5…0,6 и определяют площадь сечения в первом приближении

– по найденной площади A1 подбирают сечение и вычисляют гибкость стержня в первом приближении λ1. Зная λ, находят новое значение φ′1;

– далее, используя найденный φ′1, проверяют условие устойчивости, и если σmaxmax и [σу] значительно отличаются друг от друга (более чем на 5 %), следует повторить расчет, приняв во второй попытке

Выбор материала и рациональной формы сечения.

Выбор материала. Так как в формулу Эйлера из всех механических характеристик входит лишь модуль Юнга, то для повышения устойчивости стержней большой гибкости нецелесообразно применять высокопрочные материалы, так как модуль Юнга для всех марок сталей примерно одинаков.

Для стержней малой гибкости применение высокосортных сталей оправдано, так как с повышением предела текучести у таких сталей повышаются и критические напряжения, а значит и запас устойчивости.

Форма сечения. При проектировании стержней, работающих на устойчивость, следует выбирать такую форму сечения, чтобы гибкость стержня была одинаковой относительно обеих главных осей его сечения (условие равноустойчивости), а значит максимальный и минимальный моменты инерции такого сечения должны быть одинаковы Jmax = Jmin.

Кроме того, необходимо стремиться к получению при данной площади наибольших радиусов инерции. Для этого необходимо выбирать сечения, большая часть площади которых по возможности была удалена от центра тяжести (трубчатые, коробчатые сечения).

По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее из швеллеров, квадратное, круглое, прямоугольное.

Устойчивостью сжатых стержней называют их способность восстанавливать начальную прямолинейную форму после снятия продольной сжимающей нагрузки.

При сжатии длинных стержней их продольная ось искривляется. Такой вид деформации называется продольным изгибом.

Прямолинейный центрально сжатый стержень при определенной нагрузке (силе F) может оказаться в опасном (критическом) состоянии, при котором форма продольной оси стержня будет неустойчива.

В этом случае сколь угодно малые случайные воздействия могут вызвать большие отклонения от его первоначальной формы, вследствие чего стержень после устранения возмущений (снятия внешних нагрузок) останется в изогнутом состоянии.

Такое состояние называют потерей устойчивости прямолинейной формы стержня.

Нагрузка, при которой прямолинейная форма перестает быть формой устойчивого равновесия называется критической (F_кр).

Таким образом, исследование устойчивости стержня заключается в определении величины критической сжимающей силы F_кр.

Для обеспечения устойчивости допускаются нагрузки, составляющие лишь определенную часть от критических и называемые допустимыми силами [F]_у.

здесь, n_у – коэффициент запаса устойчивости, зависит от материала стержня.

Рекомендуемые значения коэффициента устойчивости находятся в пределах:

для стальных стоек n_у=1,5…3;
для деревянных n_у=2,5…3,5;
для чугунных n_у=4,5…5,5.

Поперечные сечения сжатых стержней должны назначаться не из условия прочности от чистого сжатия, а из условия того, чтобы сжимающие напряжения были меньше критических напряжений:

где A – площадь поперечного сечения стержня.

Критическая сила определяется по формуле Эйлера.

Вы можете изучить и скачать доклад-презентацию на тему Устойчивость сжатых стержней (продольный изгиб). Формула Эйлера. Презентация на заданную тему содержит 24 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Задача № 5 Стальной стержень (Сталь3) длинной l сжимается силой F. Требуется: Подобрать поперечное сечение сжатого стержня при допускаемом напряжении на сжатие [] = 150 МПа, пользуясь методом последовательных приближений. Вид закрепления и данные взять таблицы. Определить величину критической силы. Вычислить коэффициент запаса устой- чивости. Дано: F = 130 кН; l =2,5 м; Форма поперечного сечения: швеллер; Схема закрепления : III.

Решение: 1. Принимаем в качестве первого приближения φ1 = 0,5. Получаем: Из таблиц сортамента (ГОСТ 8239-72) выбираем швеллер № 14а, у которого А = 17,0 см2. Наименьший радиус инерции (из тех же таблиц сортамента) imin = iy = 1,84 см Гибкость стержня

Коэффициент φ1’ по таблице для стали 3 при λ = 95 равен 0,645. Так как разница между φ1 и φ1’ значительна, повторяем расчет, принимая Коэффициент φ1’ по таблице для стали 3 при λ = 95 равен 0,645. Так как разница между φ1 и φ1’ значительна, повторяем расчет, принимая Тогда Принимаем швеллер № 12, у которого А = 13,3 см2, iу = 1,53 см. Гибкость стержня

Коэффициент φ по таблице φ2’ = 0,49. Напряжение в поперечном сечении: Коэффициент φ по таблице φ2’ = 0,49. Напряжение в поперечном сечении: Допускаемое напряжение при расчете на устойчивость: []у = φ2’ * [] = 0,49*150=73,5 МПа Перенапряжение составляет: что недопустимо

Делаем еще попытку. Делаем еще попытку. Принимаем: Получаем: Принимаем швеллер № 14, у которого А = 15,6 см2, iу = 1,70 см. Получим гибкость стержня

Из таблиц коэффициент φ3’ = 0,57. Из таблиц коэффициент φ3’ = 0,57. Напряжение: Допускаемое напряжение φ3’ * [] = 0,57*150=85,5 МПа Недонапряжение: что допустимо

2. Величина критической силы 2. Величина критической силы Предельная гибкость для стали 3 λпред = 100

Примечание. Примечание. Если форма поперечного сечения окружность или прямоугольник (квадрат), то геометрические параметры сечения определяются следующим образом: 1.1. Размеры сечения: (круг) Если квадрат, то A = b2; Если прямоугольник h = 2b, то A = b * 2b = 2b2;

Читайте также: