Представление алгебраических выражений с помощью корневых деревьев доклад

Обновлено: 05.07.2024

С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу операция. В общем случае дерево при этом может оказаться не бинарным (см. рис.7).

Рис.7. Представление арифметического выражения произвольного вида в виде дерева.

Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным (см. рис.8).

Рис. 8. Представление арифметического выражения в виде бинарного дерева

Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.

Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения (см. рис.9).

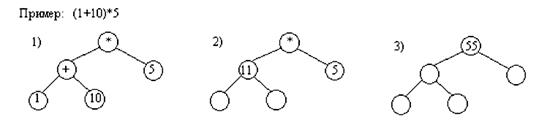
Рис.9. Вычисление арифметического выражения с помощью бинарного дерева

Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным (см. рис.10).

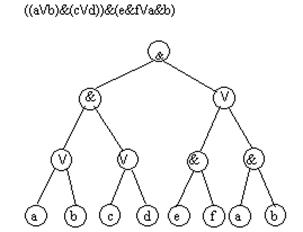
Рис. 10. Представление логического выражения в виде бинарного дерева

Контрольные вопросы

1) Понятие дерева, двоичного дерева, упорядоченного дерева, дерева поиска.

2) Способы задания дерева.

3) Способы обхода дерева (в глубину: прямой, обратный, симметричный; в ширину).

4) Показать, что бинарное дерево можно построить, если заданы прямой и обратный порядки расположения его узлов. Можно ли это сделать, если заданы прямой и концевой порядки? Если заданы обратный и симметричный порядки?

5) Найдите все бинарные деревья, узлы которых располагаются точно в одной и той же последовательности

а) в прямом и обратном порядках;

б) в прямом и симметричном порядках;

в) в обратном и симметричном порядках.

6) Каково наибольшее число вершин, находящихся одновременно в стеке при обходе двоичного дерева, содержащего n элементов:

в) симметричном порядках?

Задания для практической работы

Во всех задачах тип значений элементов дерева простой. Исходное дерево после ввода распечатать в одном из порядков.

В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при прямом обходе дерева.

2. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при обратном обходе дерева.

3. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения при концевом обходе дерева.

4. В заданном бинарном дереве подсчитать число его листьев и напечатать их значения реализуя обход, рекурсивно.

5. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при прямом обходе дерева.

6. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при обратном обходе дерева.

7. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева при концевом обходе дерева.

8. В заданном бинарном дереве найти первое вхождение заданного элемента и напечатать пройденные при поиске узлы дерева реализуя обход, рекурсивно.

9. В заданном непустом бинарном дереве найти длину (число ветвей) пути от корня до ближайшей вершины со значением равным заданному при прямом обходе дерева;

10. В заданном непустом бинарном дереве найти длину (число ветвей) пути от корня до ближайшей вершины со значением равным заданному реализуя обход, рекурсивно.

11. В заданном непустом бинарном дереве подсчитать число вершин на n- ом уровне, считая корень вершиной 0-го уровня.

12. Задано бинарное дерево. Определить, есть ли в этом дереве хотя бы два одинаковых элемента.

13. Распечатать все элементы заданного непустого бинарного дерева по уровням: сначала из корня дерева, затем (слева направо) из вершин, дочерних по отношению к корню, затем (слева направо) из вершин, дочерних по отношению к этим вершинам, и т.д.

14. Формулу вида:

::= 0|1|2|3|4|5|6|7|8|9 можно представить в виде двоичного дерева (‘дерева – формулы ‘):

- формула из одного терминала (цифры) представляется деревом из одной вершины (корнем) с этим терминалом;

- формула вида ( f₁ s f₂ ) - деревом, в котором корень – это знак s, а левое и правое поддеревья – это соответствующие представления f₁ и f₂ :

а) по заданной формуле построить дерево – формулу, обходя дерево – формулу в 1)прямом, 2)обратном, 3)концевом порядке, напечатать его элементы и вычислить (как целое число) значение;

б) проверить, является ли заданное двоичное дерево (с элементами типа char) деревом – формулой и напечатать его элементы в порядке 1)прямого, 2)обратного, 3)концевого обхода;

в) пусть в дереве – формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных; преобразовать заданное дерево – формулу, заменяя в нем все поддеревья, соответствующие формулам ( ( f₁ ± f₂ ) * f₃ ) и( f₁ *( f₂ ± f₃ ) ) на поддеревья, соответствующие формулам ( ( f₁ * f₃) ± ( f₂ * f₃ ) ) и ( ( f₁ * f₂ ) ± ( f₁ * f₃ ) ); распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке;

г) выполнить в заданном дереве – формуле преобразования, обратные преобразованиям из пункта в; распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

15. Заданную последовательность из строчных латинских букв, оканчивающуюся точкой, представить в виде дерева поиска, затем преобразовать его, удалив символ с наименьшим значением. Распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

16. Заданную последовательность из строчных латинских букв, оканчивающуюся точкой, представить в виде дерева поиска, затем преобразовать его, удалив символ с наибольшим значением. Распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

17. Заданную последовательность целых чисел, оканчивающуюся нулем, представить в виде дерева поиска, затем преобразовать его, добавив еще одно целое число; распечатать преобразованное дерево в 1)прямом, 2)обратном, 3)концевом порядке.

Литература

1. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. – М.:Вильямс, 2000. – 382 с.

2. Вирт Н. Алгоритмы и структуры данных: Пер. с англ. — 2-е изд. испр. - СПб.: Невский Диалект, 2001. -352 с.

3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики: Пер. с англ. — М.: Мир, 1998, —703с.

4. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, 2001 — 960 с.

5. Кнут Д. Искусство программирования. Т.1. – М.: Вильямс, 2000 – 690с.

6. Кнут Д. Искусство программирования. Т.2. – М.: Вильямс, 2000 – 788с.

Кнут Д. Искусство программирования. Т.3. – М.: Вильямс, 2000 – 800с.
Кубенский А. А. Структуры и алгоритмы обработки данных: объектно-ориентированный подход и реализация на C++. - СПб.: БХВ-Петербург, 2004. - 464с.

9. Липский В. Комбинаторика для программистов: Пер. с польск. М.: Мир, 1988. —213 с.

С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу √ операция. В общем случае дерево при этом может оказаться не бинарным.

Рис.. Представление арифметического выражения произвольного вида в виде дерева.

Рис. Представление арифметического выражения в виде бинарного дерева

Рис. Вычисление арифметического выражения с помощью бинарного дерева

Рис. Представление логического выражения в виде бинарного дерева

(a + b) * c - d / (e + f * g) .

Соответствующее бинарное дерево.

Рис. Бинарное дерево, представляющее

арифметическое выражение (a + b) * c – d / (e + f * g)

Тогда три варианта обхода этого дерева порождают три известные формы записи арифметического выражения:

1) КЛП - префиксную запись

- * + a b c / d + e * f g ;

2) ЛКП - инфиксную запись (без скобок, необходимых для задания последовательности выполнения операций)

a + b * c - d / e + f * g ;

3) ЛПК - постфиксную запись

a b + c * d e f g * + / - .

ЛЕКЦИЯ 12. ГРАФЫ ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. СПОСОБЫ ЗАДАНИЯ И РЕАЛИЗАЦИЯ

Цели и задачи лекции: показать способы задания и реализация графов

Основные рассматриваемые вопросы. Основные определения. Способы задания и реализация графов. Наличие циклов, связность.

Граф G - это упорядоченная пара (V, Е), где V- непустое множество вершин, Е - множество пар элементов множества V, называемое множеством ребер.

Упорядоченная пара элементов из V называется дугой. Если все пары в Е упорядочены, то граф называется ориентированным (орграфом).

Если дуга е ведет от вершины v_l к вершине v₂, то говорят, что дуга е инцидентна вершине v₂, а вершина v₂ являются смежной вершине v_v В случае неориентированного графа ребро е является инцидентной обеим вершинам v_l и v₂, а сами вершины - взаимно смежными.

Путь - это любая последовательность вершин орграфа такая, что в этой последовательности вершина в может следовать за вершиной а, только если существует дуга, следующая из а в в .

Путь, начинающийся и заканчивающийся в одной и той же вершине, называется циклом. Граф, в котором отсутствуют циклы, называется ациклическим.

Петля - дуга, соединяющая некоторую вершину сама с собой.

- Выбор структуры данных для хранения графа в памяти имеет принципиальное значение при разработке эффективных алгоритмов.

При дальнейшем изложении будем предполагать, что вершины графа обозначены символьной строкой и всего их до п, а ребер - до т. Каждое ребро и каждая вершина имеют вес - целое положительное число. Если граф не является помеченным, то считается, что вес равен единице.

Матрица смежности - это двумерный массив V, размером пХп:

При этом vij=0, если вершина i не смежна вершине; vij=весу ребра (дуги), если вершина i смежна вершине j, vij=весу петли.

Пространственная сложность этого способа V(n)~O(n 2 ). Способ очень хорош, когда надо часто проверять смежность или находить вес ребра по двум заданным вершинам.

Матрица инцидентности — это двумерный массив U размером пХт:

При этом uij=0, если вершина i не инцидентна ребру j, uij=весу ребра, если вершина инцидентна ребру j.

Списки смежных вершин - это одномерный массив размером п, содержащий для каждой вершины указатели на списки смежных с ней вершин:

Weight: integer;
Next: PNode;

TAdjacencyList = array [l..n] of record
NodeWeight: integer;
Name: string;

Пространственная сложность этого способа F_max(w)~0(w 2 ). Хранение списков в динамической памяти позволяет сократить объем расходуемой памяти, так как в этом случае не будет резервироваться место под п соседей для каждой вершины. Можно и сам массив представить в виде динамического списка, но это не имеет особого смысла, так как граф обычно является статичной (неизменяемой) структурой.

Список ребер - это одномерный массив размером т, содержащий список пар вершин, инцидентных с одним ребром графа:

Пространственная сложность этого способа V(m)~O(m). Этот способ хранения графа особенно удобен, если главная операция, которой чаще всего выполняется, это перечисление ребер или нахождение вершин и ребер, находящихся в отношениях инцидентности.

PBranch = A TBranch;

Next: PNode; end; TBranch = record

Пространственная сложность этого способа V(n, m)~O(n+m).

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.008)

С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу - операция. В общем случае дерево при этом может оказаться не бинарным.

Рис.4.16. Представление арифметического выражения произвольного вида в виде дерева.

Рис. 4.17. Представление арифметического выражения в виде бинарного дерева

Рис.4.18. Вычисление арифметического выражения с помощью бинарного дерева

Рис. 4.19. Представление логического выражения в виде бинарного дерева

4.5. Представление сильноветвящихся деревьев

До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья. Каждый элемент для представления бинарного дерева должен содержать как минимум три поля - значение или имя узла, указатель левого поддерева, указатель правого поддерева. Произвольные деревья могут быть бинарными или сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно.

Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев.

Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов.

Рис.4.20. Представление сильноветвящихся деревьев в виде списков

4.6. Применение сильноветвящихся деревьев

Один из примеров применения сильноветвящихся деревьев был связан с представлением арифметических выражений произвольного вида. Рассмотрим использование таких деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет собой одно или несколько сильноветвящихся деревьев. В файловой системе MS Dos корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью - непустым каталогам.

Рис.4.21. Представление логической структуры каталогов и файлов в виде сильноветвящегося дерева.

Для представления оглавления диска служат поля имя и тип файла/каталога. Рассмотрим программу, которая осуществляет чтение структуры заданного каталога или диска, позволяет осуществлять навигацию и подсчет места занимаемого любым каталогом.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Использование деревьев при решении алгоритмических задач

Найдите домашних животных, которые заблудились в лесу: ОРВАГЛНФЕПФНУАИГКОТОЫВАМЛОТВ ЛМКОЗАОЛЫИАОСОБАКАОЛАЛФОЛЫО ФРЛОШАДЬЫИАБРФЛИАЛОФИКОРОВА РВИЛФИЛФИХОМЯКОКППОЛАОДФЖА

Давайте покажем, как играют в крестики-нолики.

"Дерево решений" – это графическое изображение последовательности решений.

Чаще всего метод дерева решений используют в сложных, но поддающихся классификации задачах принятия решений, когда перед нами есть несколько альтернативных "решений" (проектов, выходов, стратегий), каждое из которых в зависимости от наших действий или действий других лиц (а также глобальных сил, вроде рынка, природы и т.п.) может давать разные последствия (результаты). Задача состоит в том, чтобы правильно отобразить все возможные варианты развития ситуации (ветви дерева) и конечные результаты, вычислить некоторые показатели (например, ожидаемая прибыльность проекта, затраты и т.п.) и на основе полученных данных принять решение и выборе нужной линии поведения.

Принятие решений с помощью дерева возможных вариантов производится поэтапно: Построение дерева решений (графа без циклов). Дерево строится по определенным правилам: вершины альтернативных решений, вершины событий, дуги решений, конечные решения - листья вводятся и обозначаются определенным образом в нужном порядке. Анализ дерева решений: подсчет вероятностей и математических ожиданий (стоимостных оценок решения, EMV), расчет оптимистического и пессимистического прогноза, выбор оптимального решения.

На сегодняшний день существует несколько известных алгоритмов, позволяющих создавать дерева решений: CART - аббревиатура слов Classificationand Regression Tree. Согласно его принципам, каждый узел дерева может иметь только два ответвления. С4.5 - метод построения, при котором каждый узел может иметь неограниченное количество веток. В такой схеме тяжело делать прогнозы, поэтому ее используют для классификации. QUEST (Quick, Unbiased, Efficient Statistical Trees). Самая сложная из всех моделей, но очень достоверная. Позволяет создавать многомерное ветвление. Это значит, что в любом узле может создаваться не просто множество веток, а примеров действия.

Метод построения дерева решений используют, когда нужно принять решение в условиях неопределенности, когда каждое решение зависит от исхода предыдущего или исходов испытаний, или некоторых заданных условий, появляющихся с определенной вероятностью.

Сбор данных Метод дерева решений будет эффективен в том случае, если правильно подойти к вопросу сбора данных. Приведем характерную последовательность: Определение жизненного цикла проекта: сколько будет этапов и какова продолжительность каждого из них. Выделение ключевых событий, на этапе которых может возникнуть дилемма выбрать одно или другое. Описание каждого из возможных факторов, которые повлияют на наступление того или иного события, описанного в предыдущем шаге. Оценка вероятности принятия этих решений. Расчет стоимости всех этапов жизненного цикла (считается между ключевыми событиями).

Пример дерева решений Рассмотрим типичную бизнес-ситуацию. Компании нужно выбрать выгодное инвестиционное вложение Ип1, Ип2, Ип3 с помощью дерева решений. Примеры решения задач формируются на основании исходных данных.

Первый проект требует вложения в размере 200 млн рублей и принесет прибыль 100 млн руб. Для второго необходимо 300 млн руб., но принесет 200 млн руб. Третий, самый прибыльный, - 300 млн руб., но вложить нужно 500. При этом есть риск потерять все. При первом варианте уровень риска - 10 %, при втором - 5 %, и при третьем - 20 %. Какой из проектов будет самый выгодный? Провести математические расчеты довольно затруднительно. Поэтому нужно построить графическую схему. Правильное решение будет зависеть не только от того, насколько понятной будет модель, но и как будут расположены исходные данные

Итак, у нас есть три проекта: Ип1, Ип2 и Ип3. Рассмотрим, как составить дерево решений. Двигаться будем от первого ключевого момента, обозначенного большим квадратом. Здесь мы напишем конечный итог, а пока пускай сектор остается пустым. От него чертим три ответвления с именами проектов. Далее каждый вариант имеет свой уровень математических ожиданий, обозначенный кружочком. Пока они пустые, в них нужно будет написать полученный результат расчетов. От каждого из них будет еще два ответвления. Вверх - это доход и уровень его ожидания, вниз - затраты и риски потерь.

Пора приступать к поиску правильного решения. Для этого составим формулы: Ип1= 100 × 0.9 - 200 × 0.1 = 70 Ип2 = 200× 0.95 - 300 × 0.05 = 175 Ип3 = 300 × 0.8 - 500 × 0.2 = 140

Полученные данные записываем в кружочки. Выбираем наибольшее число - 175. И записываем его в квадрат. Это и есть математическое ожидание от проекта. И поскольку самое выгодное предложение - это Ип2, это и будет являться ответом на задачу.

Задача 1 Игрок нажимает на кнопку и на экране появляется красный или зеленый круг. Если он может нажать три раза, то как часто будет побеждать? Победой считается появление друг за другом кругов разного цвета.

Читайте также: