Эллипс и гипербола доклад

Обновлено: 05.07.2024

Определение кривых второго порядка на плоскости как линий пересечения кругового конуса с плоскостями, не проходящими через его вершину. Характеристика эллипса с помощью декартовой системы координат. Понятие и основные свойства гиперболы и параболы.

Рубрика	Математика
Вид	лекция
Язык	русский
Дата добавления	25.01.2011
Размер файла	15,4 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Кривые второго порядка. Эллипс, гипербола и

парабола, их свойства и канонические уравнения. Приведение

уравнения второго порядка к каноническому виду

Кривые второго порядка

Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей - гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F1 и F2 эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему у М(х,у) координат так, чтобы ось Ох совпала с прямой F1F2, начало r1 r2 координат - с серединой отрезка F1F2. Пусть длина этого отрезка равна 2с, тогда в выбранной системе координат F1 O F2 x F1(-c, 0), F2(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F1 и F2 равна 2а.

поэтому Введя обозначение bІ = aІ-cІ и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: (11.1)

Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)

Определение 11.4. Директрисой Di эллипса, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром - начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось - малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса e a, а весь эллипс лежит в прямоугольнике)

5) Отношение расстояния ri от точки эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

Составим уравнения директрис:

(D1), (D2). Тогда Отсюда ri / di = e, что и требовалось доказать.

Гипербола

кривая плоскость эллипс гипербола парабола

Определение 11.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

если обозначить bІ = cІ - aІ, отсюда можно получить - каноническое уравнение гиперболы. (11.3)

Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.

Определение 11.7. Директрисой Di гиперболы, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах - ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением, (11.3`) для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Парабола

Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая - ее директрисой.

у Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина d M(x,y) перпендикуляра FD, опущенного из фокуса на директрису, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD D O F x равна р. Тогда из равенства r = d следует. Алгебраическими преобразованиями это уравнение можно привести к виду:

называемому каноническим уравнением параболы. Величина р называется параметром параболы.

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной - начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e 1) или параболу (при е=1).

Приведение уравнения второго порядка к каноническому виду.

Определение 11.9. Линия, определяемая общим уравнением второго порядка, (11.5) называется алгебраической линией второго порядка.

Для квадратичной формы можно задать матрицу. (11.6)

Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:

1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);

2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).

Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат - совпасть с вершиной параболы.

Поскольку в канонических уравнениях кривых второго порядка отсутствуют произведения переменных, необходимо перейти к координатной системе, определяемой базисом из ортонормированных собственных векторов матрицы А. В этом базисе уравнение (11.5) примет вид:

(в предположении, что л1,2 не равны 0).

Зададим последующий параллельный перенос формулами:

Получим в новой координатной системе уравнение. (11.7)

Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков л1, л2 и :

1) если собственные числа матрицы А л1 и л2 и одного знака, уравнение (11.7) представляет собой каноническое уравнение эллипса (случаи и, имеющего знак, противоположный знаку л1, л2, будут рассмотрены в следующей лекции).

2) если л1 и л2 имеют разные знаки, уравнение (11.7) является каноническим уравнением гиперболы: или, в зависимости от знака.

В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду, (11.8) являющимся каноническим уравнением параболы.

Приведем к каноническому виду уравнение второго порядка

3xІ + 10xy +3yІ - 2x - 14y - 13 = 0.

Матрица квадратичной формы 3xІ + 10xy + 3yІ имеет вид:

Найдем ее собственные числа и собственные векторы. Составим характеристическое уравнение: Для координат собственного вектора е1, соответствующегол1, получим с учетом нормировки, откуда e1 = <>. Аналогично найдем е2:, e2 = <>.

Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов: Тогда, подставив эти выражения в исходное уравнение, получим его вид в новой системе координат: Заметим, что коэффициентами при xІ и yІ являются л1 и л2.

Преобразуем полученное уравнение: Зададим параллельный перенос формулами. Получим уравнение, а после деления на 8 - каноническое уравнение гиперболы.

Подобные документы

Общее уравнение кривой второго порядка. Составление уравнений эллипса, окружности, гиперболы и параболы. Эксцентриситет гиперболы. Фокус и директриса параболы. Преобразование общего уравнения к каноническому виду. Зависимость вида кривой от инвариантов.

презентация [301,4 K], добавлен 10.11.2014

Математическое понятие кривой. Общее уравнение кривой второго порядка. Уравнения окружности, эллипса, гиперболы и параболы. Оси симметрии гиперболы. Исследование формы параболы. Кривые третьего и четвертого порядка. Анъези локон, декартов лист.

дипломная работа [877,9 K], добавлен 14.10.2011

Вектор в декартовой системе координат как упорядоченная пара точек (начало вектора и его конец). Линейные операции с векторами. Базис на плоскости и в пространстве. Свойства скалярного произведения. Кривые второго порядка. Каноническое уравнение параболы.

учебное пособие [312,2 K], добавлен 09.03.2009

Эллипс, гипербола, парабола как кривые второго порядка, применяемые в высшей математике. Понятие кривой второго порядка - линии на плоскости, которая в некоторой декартовой системе координат определяется уравнением. Теоремма Паскамля и теорема Брианшона.

реферат [202,6 K], добавлен 26.01.2011

Определение связи между полярными и прямоугольными координатами. Рассмотрение уравнений прямой, окружности, эллипса, гиперболы и параболы в полярных координатах. Представление в исследуемой системе координат спирали Архимеда. Построение графиков функций.

курсовая работа [1,2 M], добавлен 10.02.2012

Роль идей и методов проективной геометрии в математической науке. Закономерности кривых второго порядка и кривых второго класса, основные теоремы Паскаля и Брианшона, описывающие замечательное свойство шестиугольника вписанного в кривую второго порядка.

курсовая работа [1,9 M], добавлен 04.11.2013

Понятие матрицы, эллипса, гиперболы и параболы. Системы уравнений с матрицами. Проекция вектора на ось и действия с векторами. Плоскость и прямые линии в пространстве, их взаимное расположение. Прямоугольная декартова система координат на плоскости.

Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет.

По дисциплине Высшая математика.

Пермина Александра Николаевна

студент группы 131

Кравченко Ольга Владимировна

Кривые второго порядка: эллипс, окружность, парабола, гипербола.

Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс , при пересечении образующих обеих полостей – гипербола , а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола .

Кривая второго порядка на плоскости в прямоугольной системе координат описывается уравнением:

Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F ₁ и F ₂ есть заданная постоянная величина, называется эллипсом .

Каноническое уравнение эллипса.

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Число a называют большой полуосью эллипса , а число b – его малой полуосью .

Свойства эллипса:

Фокальное свойство. Если F₁ и F₂ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой ( F₁X ) равен углу между этой касательной и прямой ( F₂X ) .
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Эволютой эллипса является астроида.
Эксцентриситетом эллипса называется отношение . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

Эллипс также можно описать как

фигуру, которую можно получить из окружности, применяя аффинное преобразование
ортогональную проекцию окружность на плоскость.
Пересечение плоскости и кругового цилиндра.

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой её центром, на заданное ненулевое расстояние, называемое её радиусом.

Каноническое уравнение окружности.

Общее уравнение окружности записывается как:

Точка — центр окружности, R — её радиус.

Уравнение окружности радиуса R с центром в начале координат:

Свойства окружности:

Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.
Длину окружности с радиусом R можно вычислить по формуле C = 2π R .
Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы в прямоугольной системе координат:

(или , если поменять местами оси)

где р (фокальный параметр) - расстояние от фокуса до директрисы

Свойства параболы:
- Парабола — кривая второго порядка.
- Она имеет ось симметрии, называемой осью параболы . Ось проходит через фокус и перпендикулярна директрисе.
- Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе. Для параболы с вершиной в начале координат (0; 0) и положительным направлением ветвей фокус находится в точке (0; 0,25).
- Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
- Парабола является антиподерой прямой.
- Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
- При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
· Прямая пересекает параболу не более чем в двух точках.

· Эксцентриситет параболы е =1.

Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой .

Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением :

Числа и называются соответственно вещественной и мнимой полуосями гиперболы.

Свойства гиперболы:

· Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу ). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

· Каждая гипербола имеет пару асимптот: и .

· Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы .

· Эксцентриситетом гиперболы называется величина е = с / а. Эксцентриситет гиперболы e > 1

· Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы .

· Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром ..

Список литературы:

Канатиков А.Н., Крищенко А.П. Аналитическая геометрия: Учеб. для вузов. 2-е изд. / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000 – 388с.(Сер. Математика в техническом университете; Вып. III ).

Вы можете изучить и скачать доклад-презентацию на тему Замечательные кривые: Эллипс, гипербола, парабола. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Эллипс Определения и свойства: Эллипс -(от др. - греч.— недостаток.) Геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных фокусов F1 и F2 величина постоянна, то есть |F1M|+|F2M|=2a. Эллипс является коническим сечением. Коническое сечение – это пересечение плоскости с круговым конусом. Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении. Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса. Точка пересечения большой и малой осей эллипса называется его центром. Точка пересечения эллипса с осями называются его вершинами. Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b. Фокальным расстоянием называется расстояние от фокуса до центра эллипса и обозначают c. Оно вычисляется по формуле:

Эллипс Оптические свойства эллипса: 1.Эллипс – проекция окружности на плоскость не параллельно плоскости этой окружности. 2. Если сделать зеркало в форме эллипса и поместить в один из фокусов источник света, то лучи, отразившись от зеркала, соберутся в другом фокусе. Каноническое уравнение: Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса): Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Приближённая формула для периметра: При вычислении периметра эллипса всегда есть погрешность и всегда положительная. Очень приближенная формула вычисления периметра: Площадь эллипса: Площадь эллипса вычисляется по формуле:

Эллипс Эллипсы в реальности встречаются гораздо чаще, чем, кажется. Например, планеты солнечной системы движутся по эллиптическим орбитам, кольца Сатурна также имеют эллиптическую форму. В форме эллипса можно изготовить журнальный столик или соткать ковер. А у садоводов свой способ применения эллипса: в землю втыкают два колышка, крепят веревку к колышкам (один конец к одному второй к другому), верёвку оттягивают в сторону и вычерчивают эллипс с помощью палки.

Гипербола Оптические свойства: Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе. Каноническое уравнение: Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением: Равнобочная гипербола: Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением: X*Y = a2/2

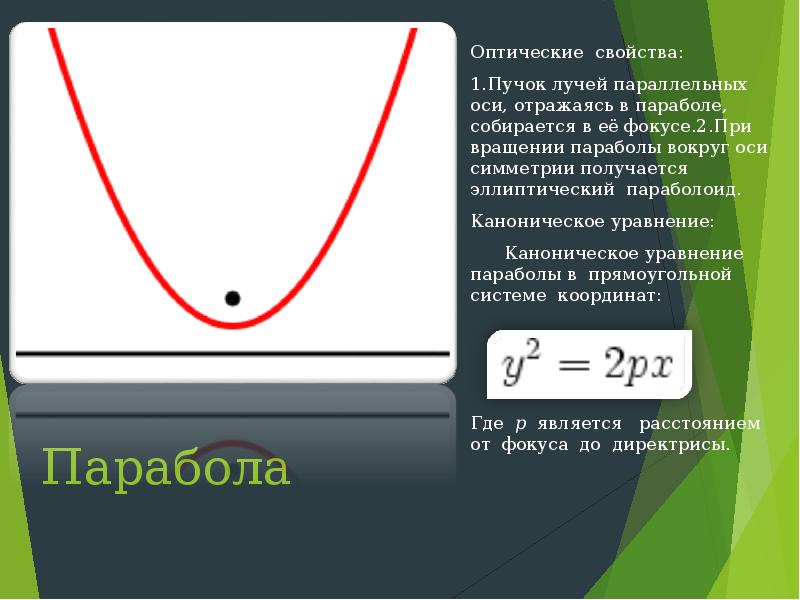
Парабола Определение и свойства: Парабола - (от греч. — приложение) —геометрическое место точек M равноудалённых от данной прямой(называемой директрисой параболы) и данного фокуса. Рассмотрим такие точки M на плоскости, которые равноудалены от фокуса F и от директрисы PQ (Это значит, что длина отрезка FM равна длине перпендикуляра, опущенного из точки M на директрису PQ) Парабола является коническим сечением. Начало координат O — середина отрезка CF. Парабола имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе. Все параболы подобны, а расстояние между фокусом и директрисой определяет масштаб.

Парабола Оптические свойства: 1.Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе.2.При вращении параболы вокруг оси симметрии получается эллиптический параболоид. Каноническое уравнение: Каноническое уравнение параболы в прямоугольной системе координат: Где p является расстоянием от фокуса до директрисы.

Парабола частое явление в повседневной жизни. Например, хорошо знакомый падающий мяч футболисты даже не подозревают, что после каждого удара они имеют дело с параболой. Ведь траектория материальной точки, брошенной в наклонном или горизонтальном направлении и падающей под действием силы притяжения Земли, имеет форму параболы. Свойство параболы о фокусировании параллельного пучка прямых используется в конструкции прожекторов, фонарей, фар, в конструкции антенн необходимых для передачи данных на большие расстояния, солнечных электростанций и т.д. Применение замечательных кривых широко распространенно, их применяют в производстве, строительстве, военном деле и т.д. Замечательные кривые поистине замечательны своими свойствами, трудно себе представить мир без этих кривых, хоть они так не заметны для нашего повседневного взора.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Эллипс.

Эллипс с каноническим уравнением $\frac+\frac=1, a\geq b>0,$ и меет форму изображенную на рисунке.

Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ - главными осями а центр симметрии $O -$ центром эллипса.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt\geq 0,$ называются фокусами эллипса векторы $\overline$ и $\overline -$ фокальными радиус-векторами, а числа $r_1=|\overline|$ и $r_2=|\overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $\frac+\frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.

Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.

Теорема. ( Директориальное свойство эллипса)

Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$

Примеры.

2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Приведем уравнение эллипса к каноническому виду:

а) Находим полуоси $a=5,$ $b=3.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt:$

$c=\sqrt=\sqrt=4\Rightarrow F_1(-4, 0),\qquad F_2(4, 0).$

г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),\qquad F_2(4, 0);$ в) $e=\frac;$ г) $D_1: x=-\frac$ и $D_2: x=\frac.$

2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=\sqrt 5.$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac=-\frac $ и $D_2: x=\frac=\frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=\sqrt 5;$ $ e=\frac.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$

2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, \sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$

Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, \sqrt 3)$ в каноническое уравнение эллипса $\frac+\frac=1:$

Таким образом, уравнение эллипса $\frac+\frac=1.$

Далее найдем координаты фокусов:

$c=\sqrt=\sqrt=2\sqrt 3\Rightarrow F_1(-2\sqrt 3, 0),\,\,\, F_2(2\sqrt 3, 0).$

Отсюда находим $\overline =(2+2\sqrt 3, \sqrt 3),$ $\overline=(2-2\sqrt 3, \sqrt 3).$

Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac>\right|.$$

Таким образом, расстояние от точки $M_1(2, \sqrt 3)$ до прямой $D_1: \sqrt 3 x+8=0$

расстояние от точки $M_1(2, \sqrt 3)$ до прямой $D_2: \sqrt 3 x-8=0$

Гипербола.

Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) - $ ее вершинами. Оси симметрии $Ox$ и $Oy$ - действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt\geq 0,$ называются фокусами гиперболы, векторы $\overline$ и $\overline -$ фокальными радиус-векторами, а числа $r_1=|\overline|$ и $r_2=|\overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.

Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$

Примеры.

2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Приведем уравнение гиперболы к каноническому виду:

а) Находим полуоси $a=3,$ $b=4.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt:$

$c=\sqrt=\sqrt=5\Rightarrow F_1(-5, 0),\qquad F_2(5, 0).$

г) Асимптоты гиперболы находим по формулам $y=\pm\fracx:$

д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),\qquad F_2(5, 0);$ в) $e=\frac;$ г) $y=\pm\fracx;$ д ) $D_1: x=-\frac$ и $D_2: x=\frac.$

2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$

Асимптоты гиперболы c центром в начале координат, находим по формулам $y=\pm\fracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=\pm\frac(x-x_0),$

$$y+3=\frac(x-2)\Rightarrow 3y+9=4x-8\Rightarrow 4x-3y-17=0.$$

$$y+3=-\frac(x-2)\Rightarrow 3y+9=-4x+8\Rightarrow 4x+3y+1=0.$$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac=-\frac $ и $D_2: x=\frac=\frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=\frac,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$

2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $\frac-\frac=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $\frac-\frac=1.$

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

$c=\sqrt\Rightarrow c=\sqrt=\sqrt =5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$

Фокальные радиусы точки, можно найти по формулам $r_1=|\overline|$ и $r_2=|\overline|.$

Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac\Rightarrow x=-\frac\Rightarrow 5x+16=0;$

$D_2: x=\frac\Rightarrow x=\frac\Rightarrow 5x-16=0;$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac>\right|.$$

Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: \sqrt 5x+16=0$

расстояние от точки $M(5, 9/4)$ до прямой $D_2: \sqrt 5x-16=0$

Ответ: $r_1=9/4,$ $r_2=\frac;$ $d_1=\frac;$ $d_2=\frac.$

2.273. Найти точки гиперболы $\frac-\frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$

Решение.

Из уравнения гиперболы находим полуоси: $a=3, \, b=4.$ Следовательно, $c=\sqrt\Rightarrow c=\sqrt=\sqrt =5.$

Отсюда находим $F_1=(-5, 0).$

Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$

Чтобы н айти точки гиперболы $\frac-\frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений

Решим уравнение $5x^2+18x-72=0:$

Находим соответствующие координаты $y:$ $y_1=\pm\sqrt=\sqrt$ - нет корней .

Ответ: $(-6, \pm4\sqrt 3).$

Парабола.

Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.

Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ - осью параболы.

Точка $F\left(\frac
, 0\right)$ называется фокусом параболы, вектор $\overline -$ фокальным радиус-векторам, а число $r=|\overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.

Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.

Примеры.

2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.

Решение.

Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $

$$y^2=6x\Rightarrow y^2=2\cdot 3x\Rightarrow p=2.$$

Ответ: $p=3.$

2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:

Ответ: $y^2=-x.$

2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$

Решение.

Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$

Приведем заданное уравнние к такому виду:

Таким образом, $y^2=4(x^2-2)$ - парабола с центром в точке $(0, 2).$ Параметр $p=2.$

Ответ: $C(0, 2),$ $p=2.$

2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$

Решение.

Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12x\Rightarrow 36=12x\Rightarrow x=3.$$

Таким образом, точка $M$ имеет координаты $(3, 6).$

Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2\cdot 6x\Rightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$

Далее находим фокальный параметр точки:

Ответ: $6.$

2.298. Из фокуса параболы $y^2=12x$ под острым углом $\alpha$ к оси $Ox$ направлен луч света, причем $tg\alpha=\frac.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2\cdot 6x\Rightarrow p=6.$

Координаты фокуса $F(p/2, 0)\Rightarrow F(3,0).$

Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $\alpha: tg\alpha=\frac$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tg\alpha=\frac.$

Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$

$0=\frac\cdot 3+b\Rightarrow b=-\frac.$ Таким образом, уравнение луча, направленного из фокуса $y=\fracx-\frac.$

Далее, найдем точку пересечения найденной прямой с параболой:

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=\frac=\frac=27.$

Таким образом, луч пересекает параболу в точке $(27, 18).$

Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$

Подставляем все найденные значения в уравнение касательной:

$y-18=\frac(x-27)\Rightarrow 3y-54=x-27\Rightarrow x-3y+27=0.$

Далее, найдем угол $\beta$ между лучем $y=\fracx-\frac$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=\frac$

$$L_2: x-3y+27=0\Rightarrow y=\fracx+9\Rightarrow k_2=\frac.$$

Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $\pi-2\beta,$ а угол между отраженным лучем и осью $Ox$ $\pi-(\pi-2\beta)-\alpha=2\beta-\alpha.$

Зная $tg\beta=\frac$ и $tg\alpha=k_1=\frac$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2\beta-\alpha):$

$$tg(2\beta-\alpha)=\frac=\frac-\frac><1+\frac\frac>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Описание презентации по отдельным слайдам:

Обоснование выбора темы реферата Я выбрала именно эту тему для создания реферата, потому что не хочется ограничиваться объемом информации из школьного курса по интересным для меня темам, кривые второго порядка одна из них. Интересно узнать различные свойства параболы, эллипса и гиперболы и многое другое о них.

Цель реферата Целью проекта является закрепление и углубление знаний по изучению свойств кривых второго порядка.

Задачи Вывести определение и уравнение параболы. Выяснить, что такое касательная к параболе и в чем заключается оптическое свойство параболы. Узнать, как строится парабола. Вспомнить определение и вывести каноническое уравнение эллипса и гиперболы. Выяснить, что такое директриса эллипса и гиперболы и их оптическое свойство. Узнать, как строится эллипс и гипербола.

История кривых второго порядка Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола.

Кривые второго порядка 1) парабола 2) эллипс 3) гипербола

Что такое парабола? Найдем множество всех точек, для каждой из которых расстояние до данной прямой равно расстоянию до данной точки, не лежащей на данной прямой. Для любой точки М(x;y) расстояние MM' до прямой d равно |y + |, а расстояние MF равно Если точка M(x;y) принадлежит искомому множеству, то MM' = MF, т. е. координаты точки М удовлетворяют уравнению |y + |=

Точка F называется фокусом, а прямая d – директрисой этой параболы. Для любой параболы существуют прямая(директриса параболы) и точка(фокус параболы), такие, что расстояние от любой точки параболы до директрисы равно расстоянию от этой точки до фокуса.

Директрисой параболы y=ax2 является прямая d, заданная уравнением y= , а фокусом – точка F (0; ) Для произвольной точки М(x;ax2), лежащей на параболе, расстояние ММ' до директрисы равно ax2+ , а расстояние MF до фокуса равно . Преобразуя подкоренное выражение, получаем, что MF= = ax2 + . ММ'=МF.

Параболой называется линия, состоящая из всех таких точек, для каждой из которых расстояние до данной прямой (директрисы параболы) равно расстоянию до данной точки ( фокуса параболы), не лежащей на директрисе.

Касательная к параболе Уравнение секущей МоМ1 имеет вид

Оптическое свойство параболы Любой луч света, исходящий из фокуса, после отражения от параболы становится параллельным оси параболы ( оси Оу).

Парабола в современном мире Параболу мы можем увидеть: в природе в струе фонтана в архитектуре

Что такое эллипс Эллипсом называется линия, состоящая из всех таких точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 имеет одно и то же значение, большее чем F1F2.

Точки F1 и F2 фокусы эллипса. 2с - расстояние между фокусами 2а – постоянная величина, равная сумме расстояний от произвольной точки эллипса до его фокусов 2с 0, а в случае гиперболы a2 – c2 1).

Если к обеим частям уравнения (2) прибавить 2xc,получится = , Числитель левой части - расстояние от точки М (х; у) до фокуса F1( -c ; o) Знаменатель - расстояние от точки М (х; у) до прямой d1 x =

Каждому фокусу эллипса ( и также гиперболы) соответствует такая прямая, что отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию от этой точки до соответствующей прямой имеет одно и то же значение. Прямые d1 и d2 называются директрисами эллипса(гиперболы).

Оптическое свойство эллипса и гиперболы В фокусе F1,помещен источник света. Тогда, любой луч света, вышедший из фокуса F1,отразившись в какой-то точке М от эллипса, проходит через фокус F2.

Возьмем на плоскости две точки F1 и F2 и рассмотрим всевозможные эллипсы и гиперболы, для которых эти точки являются фокусами. Каждая из этих гипербол пересекается с каждым эллипсом под прямым углом, т. е. угол между касательными к гиперболе и к эллипсу, проведенными через точку пересечения гиперболы и эллипса, равен 90۫۫۫۫۫۫۫۫۫۫۫۫.

Эллипс в современном мире Эллипс можно увидеть: в природе в архитектуре в обыденной жизни

Гипербола в современном мире Гиперболу можно увидеть: в природе в самолетостроении в средстве связи

Задача 1 Составить уравнение параболы, зная, что вершина ее находится в начале координат а расстояние от фокуса до вершины равно 4 единицам длины, а осью симметрии служит ось Ox. Решение. y2 = 2px и y2 = -2px. Параметр параболы p есть расстояние от директрисы параболы до фокуса. Расстояние от фокуса до вершины равно половине параметра. Значит, у нас . Подставляя это значение p в каждое из только что написанных уравнений, получим y2 = 16x и y2 = -16x. Эскизы парабол указаны на рисунках

Задача 2 Парабола симметрична относительно оси Ox, проходит через точку A(4, -1), а вершина ее лежит в начале координат. Составить ее уравнение. Решение. Так как парабола проходит через точку A(4, -1) с положительной абсциссой, а ее осью служит ось Ox, то уравнение параболы следует искать в виде y2 = 2px. Подставляя в это уравнение координаты точки A, будем иметь искомым уравнением будет Эскиз этой параболы показан на рисунке

Задача 3 Составить простейшее уравнение гиперболы, если расстояние между ее вершинами равно 20, а расстояние между фокусами 30. Решение Вершины параболы лежат на ее действительной оси. По условию 2a = 20; 2c = 30. Значит, a = 10; c = 15; a2 = 100; c2 = 225. Величины a, b, c у гиперболы связаны соотношением a2 + b2 = c2; отсюда b2 = c2 - a2 = 225 - 100; b2 = 125. Значит, уравнением гиперболы будет

Задача 4 Найти уравнение асимптот гиперболы 2x2 - 3y2 = 6. Решение У гиперболы две асимптоты, определяемые уравнениями (1) Следует найти a и b. Приведем уравнение гиперболы к простейшему виду, разделив обе его части на 6. Получим Отсюда заключаем, что . Подставляя эти значения a и b в уравнения асимптот (1) получаем и .

Задача 5 Сумма полуосей эллипса a + b = 12, а расстояние между его фокусам Составить простейшее уравнение эллипса. Решение a + b = 12, . Для определения уравнения эллипса надо знать a и b. Нам известно, что ; c2 = 18; a2 - b2 = c2. Поэтому (a + b)(a - b) = 18. Подставляя сюда a + b = 12, найдем, что a - b = 1,5. Решая систему уравнений получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде

Задача 6 Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 4; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16; Решение а) Простейшее уравнение эллипса имеет вид . Подставляя сюда a = 6, b = 4, получим б) Имеем 2c = 10; c = 5; 2a = 16; a = 8. Чтобы написать уравнение эллипса, следует найти малую полуось b. Между величинами a, b и c у эллипса существует зависимость a2 - b2 = c2, или b2 = a2 - c2. В нашем случае b2 = 64 - 25 = 39, и уравнение эллипса будет иметь вид

Краткое описание документа:

В данной работе выводится определение и уравнение параболы, канонические уравнения эллипса и гиперболы, Показано, как правильно построить параболы. Дается определение директрисы эллипса и гиперболы, приводятся их оптические свойства. А так же есть небольшой исторический материал. Имеется небольшой набор задач.

Читайте также: