Доклад по геометрии 11 класс
Обновлено: 17.05.2024
- Пусть каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1.
- Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
- Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
- Центральная симметрия пространства относительно точки O – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O. Точка O – центр симметрии.
- Осевая симметрия пространства относительно прямой m – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой . Прямая m – ось симметрии.
- Зеркальная симметрия пространства относительно плоскости α – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α. Плоскость α – плоскость симметрии.
- Параллельный перенос на вектор– преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство .
- Поворот пространства на угол φ вокруг прямой n – преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Определение движения в пространстве
Допустим, что каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1. А1 - образ точки А.
Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.
Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.
Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М', а преобразование g отображает точку М' на точку M'', то преобразование f°g отображает точку М на точку M'': f°g(М)=g(f(M))=M''.
f°g - композиция преобразований f и g.
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве
- прямые переходят в прямые,
- полупрямые — в полупрямые,
- отрезки — в отрезки,
- сохраняются углы между прямыми.
Новое свойство движения в пространстве: движение переводит плоскости в плоскости.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
Можно доказать, что композиция двух движений пространства есть движение.
2. Виды движений.
Центральная симметрия в пространстве задается и определяется так же, как и на плоскости
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.
Рисунок 1 – Центральная симметрия
На рисунке точка О – центр симметрии, АО=А1О, ВО=В1О, СО=С1О, DО=D1О (по определению точки, симметричной данной).
Центральная симметрия имеет только одну неподвижную точку – центр симметрии.
Сформулируем некоторые свойства центральной симметрии:
1) Прямая, проходящая через центр симметрии, отображается на себя.
2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).
4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.
3. Осевая симметрия (симметрия относительно прямой):
Определение:
Точка M' пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ' перпендикулярен этой прямой и делится ею пополам.
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.

Рисунок 2 – Осевая симметрия
Неподвижные точки осевой симметрии - любая точка прямой m.
Неподвижные прямые осевой симметрии:
1) сама прямая m
2) любая прямая, перпендикулярная прямой m
Неподвижные плоскости осевой симметрии:
1) любая плоскость, проходящая через прямую m
2) любая плоскость, перпендикулярная прямой m.
Зеркальная симметрия (симметрия относительно плоскости):
Определение:
Точка M' пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ' перпендикулярен этой плоскости и делится ею пополам.
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.
Рисунок 3 – Зеркальная симметрия
Неподвижные точки зеркальной симметрии - любая точка плоскости α.
Неподвижные прямые зеркальной симметрии:
1) любая прямая плоскости α
2) любая прямая, перпендикулярная плоскости α
Неподвижные плоскости зеркальной симметрии:
1) сама плоскость α
2) любая плоскость, перпендикулярная плоскости α.
Параллельный перенос (точки переносятся на данный вектор):
Рисунок 4 – параллельный перенос
Определение
Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство , называется параллельным переносом на вектор .

Перенос на нулевой вектор является тождественным преобразованием.
Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.
Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижными прямыми при параллельном переносе на вектор являются прямые, параллельные этому вектору.

Неподвижными плоскостями при параллельном переносе на вектор являются плоскости, параллельные этому вектору.
Поворот на данный угол вокруг данной оси:
Определение:
Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Рисунок 5 – Поворот вокруг прямой
Неподвижными точками являются любая точка оси вращения.
Неподвижной прямой является ось поворота.
Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.
Поворот вокруг оси на угол 180 0 является осевой симметрией.
Примеры и разбор решения заданий тренировочного модуля
Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)
В какую точку перейдет центр О пересечения медиан данного треугольника при:
Преобразование
Координата образа
Параллельный перенос на вектор (2; -2; 3)
Симметрия относительно начала координат
Симметрия относительно координатной плоскости ZOY
Поворот на угол 180 0 относительно координатной оси OZ
Симметрия относительно плоскости х=2
Найдем точку пересечения медиант данного треугольника.
Найдем координаты точки М - середины отрезка ВС:

М (); М(3; 4; 1)
Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:
Теперь найдем координаты образа точки О при каждом из преобразований:.
- Симметрия относительно начала координат задается уравнениями:

. То есть координаты образа: (-3; -2; -2)
- Симметрия относительно координатной плоскости ZOY задается уравнениями:

(ордината и аппликата точки остаются такими же, а абсцисса меняет знак). То есть координаты образа: (-3; 2; 2).
- Поворот на угол 180 0 относительно координатной оси OZ означает симметрию относительно координатной оси OZ и задается уравнениями:

(аппликата точки остается такой же, а ордината и абсцисса меняют знак). То есть координаты образа: (-3; -2; 2).
Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О хо =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную хо’ =1.
Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике.
Аксиоматический метод построения научной теории заключается в следующем : выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них.
Актуальные теоремы в геометрии
17 Декабря 2011, творческая работа
Презентация по дисциплине "Геометрия" на тему "актуальные теоремы в геометрии"
Архитектура
22 Декабря 2011, курсовая работа
Древнеримский архитектор Витрувий считал, что архитектура это совокупность трех составляющих – пользы, прочности и красоты. Эта формула остается современной и сегодня. Гармоничное сочетание функционального, конструктивного и эстетического факторов дает в результате не просто здание, а произведение архитектуры, отражающее особенности своей эпохи. Являясь продуктом синтеза искусства и техники, архитектура во все времена была отражением экономической ситуации в обществе, чутко реагировала на социальный заказ и достижения технического прогресса. Появление тех или иных типов архитектурных сооружений всегда определялось общественным укладом и национальными особенностями страны, системой религиозных верований и народными традициями.
Аффинные преобразования
20 Декабря 2012, реферат
Определение 1. Аффинным преобразованием f: Ап+Ап n-мерного аффинного пространства Аn называется такое преобразование этого пространства, при котором каждая точка с координатами (x1, . . . , xn) в некоторой системе аффинных координат переходит в точку с численно равными координатами в некоторой, вообще говоря, другой системе аффинных координат. Возьмем в аффинном пространстве An какой-нибудь вектор u=M0M1.
Векторы
25 Апреля 2012, творческая работа
Понятие вектора
Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом, называется направленным отрезком или вектором
Взаимное пересечение многогранников
27 Декабря 2011, реферат
Построение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:
1.Определяют точки, в которых ребра одной из многогранных поверхностей пересекают грани другой и ребра второй пересекают грани первой (задача на пересечение прямой с плоскостью)
Геометрические свойства равнобедренных треугольников
27 Ноября 2011, статья
Предлагаемая статья, как следует из названия, посвящена изучению свойств равнобедренных треугольников, а также установлению взаимосвязей между данными треугольниками. Необходимость исследований назрела, в первую очередь, из-за частого применения в архитектуре равнобедренных треугольников как геометрических моделей отдельных фрагментов зданий и сооружений, а во-вторых, пополнения базы знаний в области элементарной геометрии.
Геометрические характеристики плоских сечений
25 Января 2011, задача
Определить момент инерции относительно горизонтальной центральной оси плоского сечения
Определить момент инерции относительно горизонтальной центральной осиплоского сечения.
Геометрия зрения, иллюзии. Морис Эшер
19 Декабря 2011, реферат
Цель работы: объяснить зрительные иллюзии с точки зрения геометрии, увидеть и обосновать математическое начало в творчестве Мориса Эшера; углубить понимание природы зрения и восприятия в целом, в том числе иллюзорном.
Задачи исследования:
1. изучить теоретический материал по данной теме;
2. изучить и систематизировать картины Мориса Эшера;
3. найти примеры использования оптических иллюзий.
Геометрия кисти Леонардо
12 Декабря 2011, практическая работа
Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от ge — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии.
Геометрия Лобачевского
15 Апреля 2013, курсовая работа
Данная работа показывает сходство и различия двух геометрий на примере доказательства одного из постулатов Евклида и продолжение этих понятий в геометрии Лобачевского с учетом достижений науки на тот момент.
Любая теория современной науки считается верной, пока не создана следующая. Это своеобразная аксиома развития науки. Этот факт многократно подтверждался.
Физика Ньютона переросла в релятивисткую, а та - в квантовую. Теория флогистона стала химией. Такова судьба всех наук. Участь эта не обошла геометрию. Традиционная геометрия Евклида переросла в геометрии. Лобачевского. Именно этому разделу науки посвящена эта работа.
Геометрия туралы ұғым
17 Февраля 2012, реферат
Геометрия (гр. geometrіa, geo — Жер және metrio — өлшеймін) — математиканың кеңістік пішіндері мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндерді зерттейтін саласы. Фигуралар кеңістік пішіндері болып есептеледі. Геометрия тұрғысынан сызық — “сым” емес, шар — “домалақ дене” емес, олардың барлығы да — кеңістіктік пішіндер. Ал кеңістіктік қатынастар — фигуралардың мөлшері мен орналасуын анықтайды. “Тең”, “параллель”, тағыда басқа сөздер де кеңістіктік қатынастарды сипаттайды.
Геометриялық үлестіру
17 Апреля 2012, курсовая работа
Қазіргі уақытта ықтималдықтар теориясы барлық жаратылыстану, экономикалық және техникалық ғылымдар ғана емес, тіпті математикадан алшақ деп саналатын тіл ғылымына, педагогика мен психологияға, сондай-ақ социологияға, археологияға еніп, ортақ тіл табысып, ішкі құрылыс заңдарын ашатын пәрменді құралға айналып келеді кеңейтіліп, анықтала түседі де, формальданады. Оқиға ұғымы ықтималдылықтың . Ықтималдықтар теориясының бірінші негізгі ұғымы- оқиға бірте-бірте классикалық анықтамасында бастапқы ұғым болып, формальды логикалық тұрғыдан анықталмайтын жиын ұғымы ретінде түсіндірілсе, аксиоматикалық тұрғыдан оған анықтама берілді.
Дифференциация
22 Марта 2012, лекция
Дифференциа́ция (различие) — выделение частного из общей совокупности по некоторым признакам.
Иррациональные - это вещ число, кот не явл рац, то есть кот не может быть представ в виде дроби , где — целое число, —нат число
Задача по геометрии
12 Октября 2011, задача
В данную окружность вписать правильный пятнадцатиугольник.
Задачи на окружность
18 Ноября 2010, задача
Задачи на окружность
Зеркальная симметрия в пространстве
11 Ноября 2011, доклад
Рассмотрим произвольную плоскость α в пространстве и такое отображение пространства на себя, при котором каждая точка M этой плоскости остается на месте, а точка , не принадлежащая α, переходит в такую точку M1, что плоскость α перпендикулярна отрезку MM1 и проходит через его середину. Это отображение называется симметрией пространства относительно плоскости .
Золотое сечение
07 Октября 2011, реферат
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
История возникновения геометрии
17 Января 2012, реферат
Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни.
История возникновения координат на плоскости
18 Апреля 2013, реферат
История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции.
Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
История геометрии
30 Января 2011, реферат
Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от ge — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения.
История развития геометрии
18 Марта 2011, реферат
Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от geо — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения.
Касательные к эллипсу, гиперболе, параболе. Диаметры линии второго порядка
06 Мая 2012, курсовая работа
Доказательство. Достаточно рассмотреть случай, когда точка касания лежит в первой или второй четверти координатной плоскости:
Уравнение эллипса в верхней полуплоскости имеет вид:
(2)
Воспользуемся уравнением касательной к графику функции y=f(x) в точке :
(3)
Квадрики в трехмерном пространстве и их классификация
01 Декабря 2011, курсовая работа
Трехмерное пространство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так оно имеет три измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.
Конспект лекций по начертельной геометрии
30 Марта 2012, лекция
Начертательной геометрией называют науку, которая является теоретическим фундаментом черчения. В данной науке изучаются способы изображения на плоскости различных тел и их элементов. Эти изображения позволяют однозначно определить форму и размеры изделия и изготовить его. При работе с чертежами выполняются два вида работ: подготовка чертежей и их чтение.
18 Января 2011, аттестационная работа
I Конус. II Сечение конуса. III Площадь поверхности конуса. IV Объем конуса. V Усеченный конус.. VI Площадь поверхности усеченного конуса.
Концепция геометрии цивилизаций
23 Февраля 2011, научная работа
Кривые 2-го порядка как траектория движения планет
13 Мая 2013, курсовая работа
Цель работы: проанализировать законы Кеплера и, используя их, вывести уравнение траектории движения планет.
Объект изучения: законы И.Кеплера о движении небесных тел
Кривые линии и поверхности
18 Ноября 2011, реферат
Линии занимают особое положение в начертательной геометрии. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удаётся решать многие научные и инженерные задачи, решение которых аналитическим путём часто приводит к использованию чрезвычайно громоздкого математического аппарата.
Кривые линии и поверхности
30 Апреля 2012, реферат
Линии занимают особое положение в начертательной геометрии. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удаётся решать многие научные и инженерные задачи, решение которых аналитическим путём часто приводит к использованию чрезвычайно громоздкого математического аппарата.




5804442 5615980 5590887 5574992 5505230 5446671 5412373 5374770 5279331 5252995 5073109 4377304 4359578 4355509 4291737 4155688 4102458 4055480 3995142 3994742
Свидетельство и скидка на обучение каждому участнику
40%
Если Вы не нашли темы для своего учебника, то можете добавить оглавление учебника и получить благодарность от проекта "Инфоурок".
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Время чтения: 2 минуты
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы
Время чтения: 0 минут
В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик
Время чтения: 2 минуты
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.
Что такое центральная симметрия
Начнём с определения: центральная симметрия - одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.
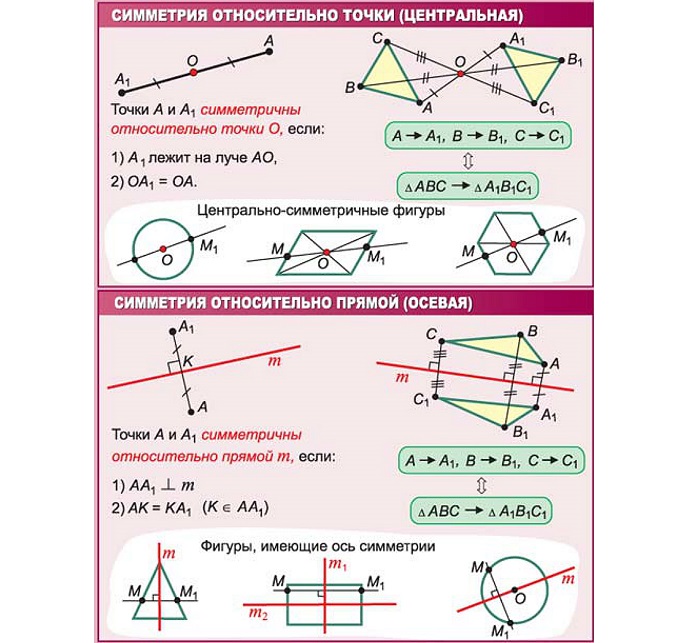
Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.
Свойства центральной симметрии
Основные свойства следующие:
1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.
Посмотрим на рисунок. Треугольники АВС и А1В1С1 симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А1О, ВО=В1О, СО=С1О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;
2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;
3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;
4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.
Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А1В1 относительно точки О.
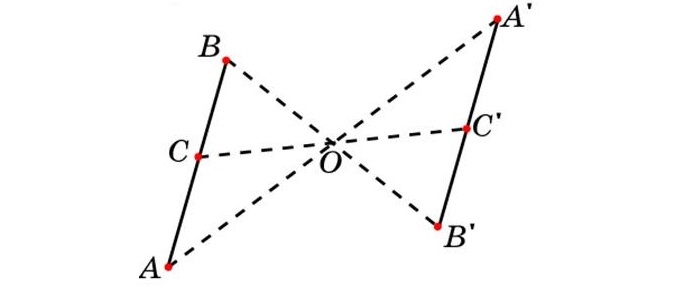
Далее соединяем симметричные точки и получаем отрезки АА1 и ВВ1. Далее легко заметить, что отрезки АО и А1О будут равны. Соответственно равны и отрезки ВО и В1О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.
Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А1 и В,В1. Значит они являются накрест лежащими при секущих АА1 и ВВ1. Задача решена, АВ и А1В1 параллельны;
5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.
Примеры фигур, обладающих центральной симметрией
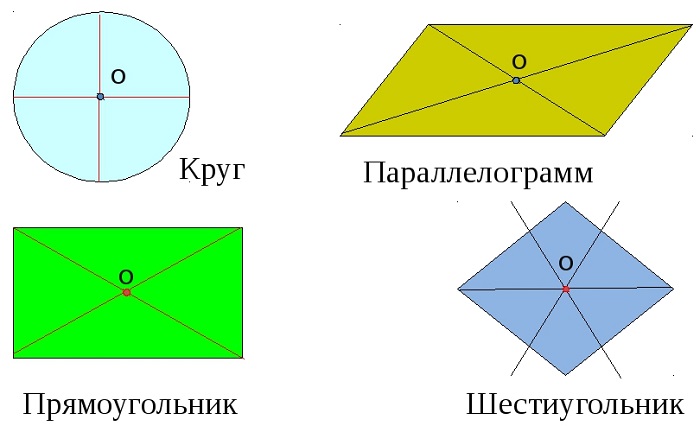
Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:
различные правильные многоугольники.
Интересные факты о центральной симметрии
Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.
Ещё один очевидный пример – бабочка.

Великолепные узоры на её крылышках – четкая и яркая симметрия.
Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.
Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.
Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.
Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.
Читайте также:

