Доклад медиана 7 класс

Обновлено: 25.06.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Высота, медиана и биссектриса треугольника Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из данной вершины к прямой, проходящей через противоположную сторону. А В С К М N S СК – высота треугольника АВС MS – высота треугольника РМN

У любого треугольника – три высоты: Высоты перпендикулярны прямым, содержащим противоположные стороны. Три высоты треугольника пересекаются в одной точке – в точке О. Сделай в тетради такой же рисунок, запиши высоты треугольника АВС. Укажи прямые углы. А В С А1 В1 С1 О

Высота, медиана и биссектриса треугольника Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. А В С К М N P S СК – биссектриса треугольника АВС MS – биссектриса треугольника РМN

У любого треугольника – три биссектрисы: Биссектрисы делят углы треугольника пополам. Три биссектрисы треугольника пересекаются в одной точке – в точке О. Сделай в тетради такой же рисунок, запиши биссектрисы треугольника АВС. Укажи равные углы. А В С А1 В1 С1 О

Высота, медиана и биссектриса треугольника Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны. А В С К М N P S СК – медиана треугольника АВС MS – медиана треугольника РМN

У любого треугольника – три медианы: Медианы делят противоположные стороны треугольника пополам. Три медианы треугольника пересекаются в одной точке – в точке О. Сделай в тетради такой же рисунок, запиши медианы треугольника АВС. Укажи равные отрезки. А В С А1 В1 С1 О

Равнобедренный треугольник А В С Треугольник называется равнобедренным, если у него две стороны равны. АВ=ВС Равные стороны называются боковыми, а третья сторона – основанием. АВ и ВС – боковые стороны. АС – основание.

Равносторонний треугольник А В С Треугольник, у которого все стороны равны, называется равносторонним. АВ=ВС=АС  Треугольник АВС - равносторонний 1. В равностороннем треугольнике все углы равны по 60°. 60° 60° 60° 2. В равностороннем треугольнике биссектриса, высота и медиана, проведенные из одной вершины, совпадают.

Свойство углов равнобедренного треугольника А В С Угол между боковыми сторонами равнобедренного треугольника называется углом при вершине. В - угол при вершине. Углы А и С называются углами при основании. Углы при основании равнобедренного треугольника равны: АВС - равнобедренный Обратно: А = С   А = С. Если в треугольнике два угла равны, то такой треугольник равнобедренный. АВС - равнобедренный.

Сделай в тетради такой же рисунок и ответь письменно на вопросы: М N Р Если в  МNP MN=NP, то что можно сказать про углы М и Р ? Почему? К R S Если в  KRS S=R, то что можно сказать про его стороны ? Почему? Подсказка

Свойство медианы равнобедренного треугольника А В С В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. D АВС – равнобедренный(АВ=ВС), АD = СD(ВD- медиана)  АВD = CBD, ВD  АC.

Образец решения задачи В А С 1.Периметр равнобедренного треугольника равен 26 см. Найти боковые стороны, если основание равно 6 см. Дано:  АВС – равнобедр., АС=ВС, Р=26 см, АВ=6см. Найти: АС, ВС. Решение: Р=АВ+АС+ВС, АС=ВС  Р=АВ+2АС, 2АС=Р – АВ = 26 – 6 = 20,  АС = 20 : 2 = 10. Ответ: АС=ВС=10 см.

Образец решения задачи В А С 2.В равнобедренном треугольнике боковая сторона на 3 см больше основания, а периметр равен 27 см. Найти стороны треугольника. Дано:  АВС – равнобедр., АС=ВС, Р=27 см, АС>АВ на 3 см. Найти: АВ, АС, ВС. Решение: Р=АВ+АС+ВС, Пусть АВ=х, тогда АС=ВС=х+3. Составим уравнение: х+х+3+х+3=27  Ответ: АВ= 7 см, АС=ВС=10 м. 3х+6=27  3х=27 – 6=21  х=21 : 3 = 7  АВ= 7 см, АС=ВС= 7+3=10 см.

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 602 944 материала в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

13.04.2020 568
PPTX 863.5 кбайт
13 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Филиппова Татьяна Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Время чтения: 1 минута

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Студенты российских вузов смогут получить 1 млн рублей на создание стартапов

Время чтения: 3 минуты

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Геометрия начинается с треугольника. Вот уже два тысячелетия треугольник является как бы символом геометрии, но он не символ. Треугольник – атом геометрии.

Треугольник неисчерпаем – постоянно открываются его новые свойства. Чтобы рассказать о всех известных его свойствах, необходим том сравнимый по объему с томом Большой энциклопедии. Мы хотим рассказать о медиане треугольника и ее свойствах, а так же о применении медиан.

Сначала вспомним, что медиана треугольника – это отрезок соединяющий вершины треугольника с серединой противоположной стороны. Медианы имеют множество свойств. Но мы рассмотрим одно свойство и 6 различных его доказательств. Три медианы пересекаются в одной точке, которая называется центроидом (центром масс) и делятся в отношении 2:1.

Существует медианы не только треугольника, но и тетраэдра. Отрезок, соединяющий вершину тетраэдра с центроидом (точкой пересечения медиан) противолежащей грани называется медианой тетраэдра. Мы так же рассмотрим свойство медиан тетраэдра.

Медианы используются в математической статистике. Например, для нахождения среднего значения некоторого набора чисел.

1. Медианы треугольника и их свойства

Как известно, медианами треугольника называются отрезки, соединяющие его вершины с серединами противоположных сторон. Все три медианы пересекаются в одной точке и делятся ею в отношении 1:2.

Точка пересечения медиан является также центром тяжести треугольника. Если подвесить картонный треугольник в точке пересечения его медиан то он будет находиться в состоянии равновесия

Любопытно, что вcе шесть треугольников, на которые всякий треугольник разбивается своими медианами, имеют одинаковые площади.

Медианы треугольника через его стороны выражаются так:

Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.

Построим треугольник, стороны которого равны медианам данного треугольника, тогда медианы построенного треугольника будут равны 3/4 сторон первоначального треугольника.

Данный треугольник назовем первым, треугольник из его медиан - вторым, треугольник из медиан второго - третьим и т. д. Тогда треугольники с нечетными номерами (1,3, 5, 7. ) подобны между собой и треугольники с четными номерами (2, 4, 6, 8. ) также подобны между собой.

Сумма квадратов длин всех медиан треугольника равняется ¾ суммы квадратов длин его сторон.

2. Открытие немецкого математика Г. Лейбница

Знаменитый немецкий математик Г. Лейбниц обнаружил замечательный факт: сумма квадратов расстояний от произвольной точки плоскости до вершин треугольника, лежащего в этой плоскости, равняется сумме квадратов расстояний от точки пересечения медиан до его вершин, сложенной с утроенным квадратом расстояния от точки пересечения медиан до выбранной точки.

Из этой теоремы следует, что точка на плоскости, для которой сумма квадратов расстояний до вершин данного треугольника является минимальной,- это точка пересечения медиан этого треугольника.

В то же время минимальная сумма расстояний до вершин треугольника (а не их квадратов) будет для точки, из которой каждая сторона треугольника видна под углом в 120°, если ни один из углов треугольника не больше 120° (точка Ферма), и для вершины тупого угла, если он больше 120°.

Из теоремы Лейбница и предыдущего утверждения легко найти расстояние d от точки пересечения медиан до центра описанной окружности. Действительно, это расстояние по теореме Лейбница равно корню квадратному из одной трети разности между суммой квадратов расстояний от центра описанной окружности до вершин треугольника и суммой

Квадратов расстояний от точки пересечения медиан до вершин треугольника. Получаем, что

Точка М пересечения медиан треугольника AВС является единственной точкой треугольника, для которой сумма векторов МА, MB и МС равна нулю. Координаты точки М (относительно произвольных осей) равны средним арифметическим соответствующих координат вершин треугольника. Из этих утверждений можно получить доказательство теоремы о медианах.

3. Применение медиан в математической статистике

Медианы бывают не только в геометрии, но и в математической статистике. Пусть нужно найти среднее значение некоторого набора чисел ,, . а_п . Можно, конечно, за среднее принять среднее арифметическое

Но иногда это неудобно. Допустим, что нужно определить средний рост второклассников Москвы. Опросим наугад 100 школьников и запишем их рост. Если один из ребят в шутку скажет, что его рост равен километру, то среднее арифметическое записанных чисел окажется слишком большим. Гораздо лучше в качестве среднего взять медиану чисел , . а_п .

Предположим, что чисел - нечетное количество, и расставим их в неубывающем порядке. Число, оказавшееся на среднем месте, называется медианой набора. Например, медиана набора чисел 1, 2, 5, 30, 1, 1, 2 равна 2 (а среднее арифметическое значительно больше - оно равно 6).

4. Медианы тетраэдра

Оказывается, можно говорить о медианах не только для треугольника, но и для тетраэдра. Отрезок, соединяющий вершину тетраэдра с центроидом (точкой пересечения медиан) противолежащей грани, называется медианой тетраэдра. Как и медианы треугольника, медианы тетраэдра пересекаются в одной точке, центре масс или центроиде тетраэдра, но отношение, в котором они делятся в этой точке, иное – 3:1, считая от вершин. Эта же точка лежит и на всех отрезках, соединяющих середины противоположных ребер тетраэдра, его бимедианах, и делит их пополам. Это можно доказать, например, из механических соображений, поместив в каждую из четырех вершин тетраэдра грузики единичной массы.

5. Шесть доказательств теоремы о медианах

Давно замечено, что познакомиться с разными решениями одной задачи бывает полезнее, чем с однотипными решениями разных задач. Одной из теорем, допускающих, как и многие другие классические теоремы элементарной геометрии, несколько поучительных доказательств, является

Теорема о медианах треугольника. Медианы , В и С треугольника ABC пересекаются в некоторой точке М, причем каждая из них делится этой точкой в отношении 2:1, считая от вершины: AM : M = BM : M = CM : M =2. (1)

Во всех приводимых далее доказательствах, кроме шестого, мы устанавливаем только, что медиана В проходит через точку М, которая делит медиану А в отношении 2:1. Если в соответствующем рассуждении заменить отрезок В на отрезок С, то мы получим, что и С проходит через М. Этим будет доказано, что все три медианы пересекаются в некоторой точке М, причем АМ:М - 2. Поскольку все медианы равноправны, можно заменить А на В или СС₁ отсюда вытекает (1).

Первое доказательство (8 класс).

Пусть К - середина отрезка AM , В' - точка пересечения прямой ВМ со стороной АС. Нам достаточно доказать, что АВ' = В'С. Через точки К и параллельно прямой ВМ проведем отрезки KL и N (рис. 1). Поскольку АК - КМ = М и С=В, по теореме Фалеса получаем

AL = LB ' = B ' N =; NC .

Второе доказательство(8 класс).

Рассмотрим гомотетию с центром М и коэффициентом -1/2. Точка А переходит при этой гомотетии в . Пусть В переходит в В' (рис. 2). Тогда = - АВ. С другой стороны, средняя линия получается из стороны ВА при гомотетии с центром С и коэффициентом 1/2; таким образом:

Итак, , следовательно, В'=. Таким образом, треугольники ABC и гомотетичны, причем центр гомотетии лежит в точке М. По определению гомотетии, точки В, М и В' = лежат на одной прямой.

Третье доказательство(9 класс).

Рассмотрим треугольники MAC и МС (рис. 3). Их высоты, опущенные из вершины С, совпадают, а длины противолежащих этой вершине сторон относятся как 2:1, поэтому , где S обозначает площадь. Аналогично, . Но . Следовательно,

. Таким образом, треугольники МАВ, МВС и МСА равновелики. Пусть В' - точка пересечения прямых ВМ и АС. Докажем, что АВ' = В'С. С одной стороны,

С другой стороны,

отсюда получаем

Четвертое доказательство (9 класс).

ВМ= ВС + СА+АМ=ВС + СА+

Следовательно, точка М лежит на медиане .

Пятое доказательство (9 класс).

Опять рассмотрим точку В' пересечения прямых ВМ и АС (рис. 3). Применяя теорему синусов сначала к треугольникам АВ'В и СВ'В, а затем - к треугольникам АВМ и ВМ и учитывая, что sinAB ' B = sinCB ' B , sinAMB = = sinMB , BC=2Bи МА = 2M, получим

Шестое доказательство(10 класс).

Проведем через точки А и В плоскость а, не содержащую С, и построим в этой плоскости правильный треугольник ABC (рис. 5). Из общих свойств параллельной проекции следует, что параллельная проекция вдоль прямой С переводит треугольникАВС в треугольник АВ, причем медианы треугольника ABC проектируются в медианы треугольника AB . Но в правильном треугольнике медианы являются и биссектрисами, а следовательно, пересекаются в одной точке. Легко доказать также (докажите!), что для треугольника AB справедливы равенства (1).

Отсюда вытекает, что наша теорема верна и для треугольника АВС.

Упомянем еще одно, быть может, самое простое и естественное доказательство теоремы о медианах: если поместить в вершины треугольника равные массы и поочередно группировать их парами, мы получим, что центр всех трех масс лежит на каждой из медиан. Центр системы равных масс, помещенных в некоторые точки, называется центроидом этого набора точек, поэтому и точку пересечения медиан треугольника часто называют его центроидом.

Исходя из проделанной работы можно сделать следующие выводы:

2. Медиана была изучена многими учеными, но особый вклад в ее развитие внес немецкий ученый Г. Лейбниц. Он обнаружил замечательный факт: сумма квадратов расстояний от произвольной точки плоскости до вершин треугольника, лежащего в этой плоскости, равняется сумме квадратов расстояний от точки пересечения медиан до его вершин, сложенной с утроенным квадратом расстояния от точки пересечения медиан до выбранной точки.

Из этой теоремы следует, что точка на плоскости для которой сумма квадратов расстояний до вершин данного треугольника является минимальной, - это точка пересечения медиан этого треугольника.

3. Медианы используются не только в геометрии, но и в физике, и в статической математике. Для вычисления среднего арифметического и др.

Список использованных источников и литературы

1. И.Л. Никольская. Факультативный курс по математике. Учебное пособие для 7-9 классов средней школы. Москва “Просвещение” 1991 г. с. 92-93.

2. Т.Л. Рыбакова, И.В. Суслова. Школьный справочник “МАТЕМАТИКА”. Ярославль “Академия развития” 1997 г. с. 113.

3. Ежемесячный научно-популярный физико-математический журнал Академии наук СССР и Академии педагогических наук литературы. “ Квант № 7 1990 г. с. 40.

4. Ежемесячный научно-популярный физико-математический журнал Академии наук СССР и Академии педагогических наук литературы. “ Квант № 1 1990 г. с. 54.

1. Докажите, что точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной прямой. Вывести отсюда теорему о медианах.

2. Дан треугольник ABC . Укажите все такие точки P , что S_PAB = S_PBC = S_PCA .

3. Каждая из вершин пятиугольника соединена с серединой противолежащей стороны. Докажите, что если четыре из полученных прямых пересекаются в одной точке, то и пятая прямая проходит через эту точку.

4. Через каждое из ребер трехгранного угла и биссектрису противоположного плоского угла проведена плоскость. Докажите, что три полученные плоскости имеют общую прямую.

5. Точки A ₁ , B ₁ , C ₁ лежат соответственно на сторонах BC , CA и AB треугольника ABC . Известно, что отрезки AA ₁ , BB ₁ , CC ₁ пересекаются в точке P , причем

Цели урока: образовательные: ввести понятие медианы, организовать деятельность учащихся по закреплению медианы, среднего арифметического, размаха и моды, обеспечить отработку навыка их применения при выполнении различных заданий; развивающие: способствовать развитию логического мышления учащихся; воспитательные: воспитывать интерес к изучаемому предмету.

Тип урока: учебное занятие изучения нового материала в форме исследования и закрепления знаний и способов деятельности.

Ход занятия

I. Организация начала занятия

II. Проверка домашнего задания

(если нет вопросов, собрать тетради с д/з, а если есть вопросы, их разобрать используя готовое решение)

№172 (слайд 1)

№175(слайд 2)

В ряду чисел 2, 7, 10, __ , 18, 19, 27 одно из чисел оказалось стертым. Восстановите его, зная, что среднее арифметическое этих чисел равно 14.

Решение:

Обозначим неизвестное число х ; всего чисел в ряду 7, поэтому

III. Актуализация опорных знаний учащихся

1. Фронтальный опрос. (слайд 3)

1) Что называется средним арифметическим ряда чисел? Может ли среднее арифметическое ряда чисел не совпадать ни с одним из этих чисел?

2) Что называется размахом ряда чисел?

3) Что называется модой ряда чисел? Любой ли ряд чисел имеет моду? Может ли ряд чисел иметь более одной моды? Может ли мода ряда чисел не совпадать ни с одним из этих чисел?

2. Тест (текст одинаков для всех, на презентации слайд 4).

1. Среднее арифметическое разных чисел всегда бывает

а) больше меньшего из чисел;
б) меньше меньшего из чисел;
в) больше большего из чисел.

2. Среднее арифметическое чисел 4,2; 0,08; 0,01 равно:

3. В волейбольной команде двум игрокам по 21 году, трём — по 20 лет, а одному — 24 года.

Средний возраст игроков команды составляет:

Ответы

а)
а) (4,2+0,08+0,01):3=1,43
б) (21+21+20+20+20+24):6=21 год

3. Устная практическая работа по таблице в презентации (слайд 5)

Рассмотрите таблицу и ответьте на следующие вопросы:

1)1,6 + 3,4 =; 2) 3,8 + 6,4 + 6,2 =; 3) – 10,2 + 18,4 =; 4) 2,3 · 6 =; 5) 7,43 – 5 =; 6) 15,25 : 5 = ; 7) Что больше: 2,345 или 2,43?

8,2	2,43	16,4	5	3,05	13,8
д	а	е	м	н	и

В результате устного счёта получилось слово медиана.

Проблема: Что такое медиана?

IV. Изучение нового материала

Задача урока: изучить определение медианы, закреплять его при выполнении упражнений, развивать умение вычислять среднее арифметическое, определять размах и моду при выполнении различных заданий, развивать логическое мышление.

В таблице показан расход электроэнергии в январе жильцами девяти квартир: (таблица в презентации слайд 7)

64, 72, 72, 75, 78, 82, 85, 91, 93.

64, 72, 72, 75, 78, 82, 85, 88, 91, 93.

В этом числовом ряду четное число членов и имеются два числа, расположенные по середине ряда: 78 и 82.

Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы: слева от него находится пять членов ряда и справа тоже пять членов ряда:

Говорят, что в этом случае медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.

Определение: (слайд 8) Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Если в упорядоченном числовом ряду содержится 2п -1 членов, то медианой ряда является п-й член, так как n-1 членов стоит до n-го члена и п -1 членов — после n-го члена. Если в упорядоченном числовом ряду содержится 2п членов, то медианой является среднее арифметическое членов, стоящих на n-м и п + 1-м местах.

В каждом из рассмотренных выше примеров, определив медиану, мы можем указать номера квартир, для которых раcход электроэнергии жильцами превосходит срединное значение, т.е. медиану.

2) Работа по учебнику

Рассмотреть пример на странице 40 в учебнике и сделать вывод:

Такие показатели как среднее арифметическое, мода и медиана, по-разному характеризуют данные, полученные в результате наблюдений. Поэтому на практике при анализе данных в зависимости от конкретной ситуации используются либо все три показателя, либо некоторые из них. Далее рассмотреть примеры в учебном пособии.

- Физкультминутка для глаз.

V. Первичное закрепление изученного материала

- Выполнить № 186 (а, г)- (комментированное письмо).

Решение:

а) 30, 32, 37, 40, 41, 42, 45, 49, 52; г) 1,2; 1,4; 2,2; 2,6; 3,2; 3,8; 4,4; 5,6; = 2,9.

Ответ: а) 41; г) 2,9.

VI. Закрепление изученного материала

№188 (устно)

Решение:

а) может, если сумма членов не кратна числу членов;
б) не может, так как разность двух натуральных чисел, из которых уменьшаемое больше вычитаемого, есть число натуральное;
в) не может, так как мода – один из членов ряда, а все члены ряда – натуральные числа;
г) может, если число членов ряда четное и числа, стоящие по средине не равны между собой.

Ответ: а) да; б) нет; в) нет; г) да.

№190 (самостоятельно, с последующей проверкой)

Решение: число членов ряда равно 16, для нахождения медианы ряд нужно упорядочить:

1, 2, 2, 3, 3, 4, 4, 4, 5, 6, 8, 10, 10,10, 12, 25.

Медиана ряда = 4,5.

Число приобретённых акций превосходит медиану у следующих сотрудников:

Астахова
Павлов
Петрова
Волков
Куликова
Райков
Осипов
Лаврова

VII. Итог урока (слайд 9)

Что называется медианой ряда чисел?
Может ли медиана ряда чисел не совпадать ни с одним из этих чисел?
Какое число является медианой упорядоченного ряда, содержащего нечётное число чисел; четное число чисел?

VIII. Задание на дом:

П. 10, вопросы на стр. 42,43, №186(б, в), №189, №191, №195 (повторение),

IX. Рефлексия

(в форме выполнения теста по трём вариантам, индивидуально), а на следующем уроке сдаются тетради для проверки и оценки результатов.

Этот урок начинаем с повторения уже известных нам статистических характеристик. И вводим понятие еще одной характеристики числового ряда, которую называют медианой.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Медиана как статистическая характеристика"

На предыдущем уроке мы с вами познакомились с тремя статистическими характеристиками.

На этом уроке мы познакомимся с ещё одной статистической характеристикой.

Давайте рассмотрим таблицу, в которой показано число посетителей музея в разные дни недели.

Составим из данных, приведённых в таблице, упорядоченный ряд.

В этом ряду семь чисел. Посмотрите, что в середине ряда расположено число 175: слева от него расположены 3 числа и справа тоже 3 числа. Число 175 называют срединным числом, или медианой упорядоченного ряда.

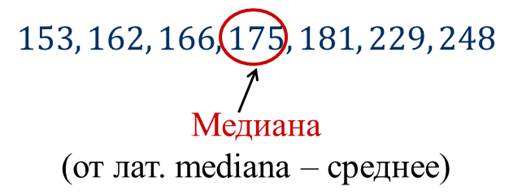
Число 175 считают и медианой исходного (неупорядоченного) ряда.

Теперь рассмотрим таблицу, в которой показано число посетителей музея в разные дни в течение двух недель.

Снова составим из приведённых данных упорядоченный ряд.

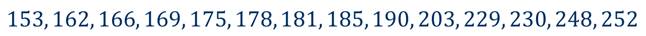
Обратите внимание, что в этом ряду чётное количество чисел, и поэтому мы не можем выбрать одно число, расположенное в середине и выберем два – 181 и 185.

Найдём среднее арифметическое этих чисел, то есть их сумму разделим на 2, и получим 183. Число 183 разбивает наш ряд на две равные по численности группы (слева от него находятся 7 чисел ряда и справа – 7 чисел ряда) и является медианой упорядоченного ряда и исходного. При этом обратим внимание, что само число 183 не является членом ряда.

В каждом из рассмотренных примеров, найдя медиану ряда, мы можем указать дни, когда количество посетителей музея превосходит срединное значение, то есть медиану, или, наоборот, меньше этого значения.

Определение.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине.

А медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, расположенных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Читайте также: