Действия над комплексными числами в алгебраической и тригонометрической форме доклад
Обновлено: 05.07.2024
Комплексным числом [latex]z[/latex] называется число вида [latex]z=a+bi[/latex], где [latex]a[/latex] и [latex]b[/latex] – действительные числа, [latex]i[/latex] – так называемая мнимая единица. Число [latex]a[/latex] называется действительной частью [latex](Rez)[/latex] комплексного числа, число [latex]b[/latex] называется мнимой частью [latex](Imz)[/latex] комплексного числа.
Сложение
Пусть [latex]z_1,z_2\in C[/latex], [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_2+b_2i[/latex].
Тогда [latex]z=[/latex] [latex]z_1 + z_2[/latex] получается простым приведением подобных:
[latex]z_1 + z_2=[/latex] [latex]z_1 + z_2=[/latex] [latex]a_1+b_1i+a_2+b_2i=[/latex] [latex](a_1+a_2)+(b_1+b_2)i[/latex]
[latex]z_1=3+2i[/latex] и [latex]z_2=1+4i[/latex]
[latex]z_1 + z_2=[/latex] [latex]3+2i + 1+4i=[/latex] [latex](3+1)+(2+4)i=[/latex] [latex]4+6i[/latex]
Вычитание
Пусть [latex]z_1,z_2\in C[/latex], [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_2+b_2i[/latex].
Тогда [latex]z=[/latex] [latex]z_1 — z_2[/latex] получается аналогично со сложением:
[latex]a_1+b_1i — (a_2+b_2i)=[/latex] [latex](a_1-a_2)+(b_1-b_2)i[/latex]
[latex]z_1=6+i[/latex] и [latex]z_2=5+2i[/latex]
[latex]z_1 — z_2=[/latex] [latex]6+i — (5+2i)=[/latex] [latex](6-5)+(1-2)i=[/latex] [latex]1-i[/latex]
Умножение
Пусть [latex]z_1,z_2\in C[/latex], [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_2+b_2i[/latex].
Тогда [latex]z=[/latex] [latex]z_1 \times z_2=[/latex] [latex](a_1+b_1i) \times (a_2+b_2i)[/latex].
Что делать на этом шаге? Все довольно просто, как Вы наверно и подумали, надо всего лишь раскрыть скобки и привести подобные:
[latex](a_1+b_1i) \times (a_2+b_2i)=[/latex] [latex](a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i[/latex]
Определение комплексно сопряженного числа
Пусть [latex]z_1,z_2\in C[/latex], [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_2+b_2i[/latex].
[latex]z_1[/latex] называют комплексно сопряженным к [latex]z_2[/latex], если [latex]a_1 = a_2[/latex] и [latex]b_1 = -b_2[/latex], т.е. [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_1-b_1i[/latex].
И при перемножении [latex]z_1 \times z_2=[/latex] [latex]^2-^2[/latex]
Это потребуется для нашего следующего действия.
Деление
Пусть [latex]z_1,z_2\in C[/latex], [latex]z_1=a_1+b_1i[/latex] и [latex]z_2=a_2+b_2i[/latex].
Тогда [latex]z=[/latex] [latex]\frac=[/latex] [latex]\frac[/latex]
На этом шаге обычно все и остановилось бы, но мы сможем еще упростить выражение благодаря знанию комплексно сопряженных чисел. Умножим числитель и знаменатель на комплексно сопряженное число к знаменателю, получим:
[latex]\frac=[/latex] [latex]\frac^2+^2>[/latex]
Перед дальнейшим прочтением материала просмотрите информацию о тригонометрической форме комплексного числа
Любое комплексное число [latex]z[/latex] можно представить в виде:[latex]|z|(\cos\phi+ i\sin\phi)[/latex], где [latex]|z|[/latex] — это модуль комплексного числа, а [latex]\phi=arg z[/latex] — это аргумент комплексного числа. [latex]|z|=\sqrt[/latex]
Умножение
Произведением двух комплексных чисел [latex]z_1=r_1(cos\phi_1+isin\phi_1)[/latex] и [latex]z_2=r_2(cos\phi_2+isin\phi_2)[/latex] будет комплексное число вида [latex]z=z_1z_2=r_1r_2(\cos(\phi_1+\phi_2)+i\sin(\phi_1+\phi_2)[/latex]
[latex]z_1=3(\cos\frac<2\pi>+i\sin\frac<2\pi>)[/latex] и [latex]z_1=2(\cos\frac<\pi>+i\sin\frac<\pi>)[/latex]
[latex]z_1 \times z_2=[/latex] [latex]3(\cos\frac<2\pi>+i\sin\frac<2\pi>) \times 2(\cos\frac<\pi>+i\sin\frac<\pi>)=[/latex] [latex]6(\cos\frac<7\pi>+i\sin\frac<7\pi>)[/latex]
Деление
Частным двух комплексных чисел [latex]z_1=r_1(cos\phi_1+isin\phi_1)[/latex] и [latex]z_2=r_2(cos\phi_2+isin\phi_2)[/latex] будет комплексное число вида [latex]z=z_1z_2=\frac(\cos(\phi_1-\phi_2)+i\sin(\phi_1-\phi_2)[/latex]
Возведение в степень
[latex]\forall z \in C[/latex] [latex]z^n=[/latex] [latex]
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
2. История развития комплексных чисел.
3. О комплексных числах.
4. Соглашение о комплексных числах
5. Сложение комплексных чисел
6 . Вычитание комплексных чисел.
7. Умножение комплексных чисел.
8. Деление комплексных чисел.
9. Модуль и аргумент комплексного числа.
10. Тригонометрическая форма комплексного числа.
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.
История развития комплексных чисел.
Д ля решения алгебраических уравнений недостаточно действительных чисел. Поэтому естественно стремление сделать эти уравнения разрешимыми, что в свою очередь приводит к расширению понятия числа. Например, для того чтобы любое уравнение х+а =в имело корни, положительных чисел недостаточно и поэтому возникает потребность ввести отрицательные числа и нуль. Древнегреческие математики считали, что а = с и в = а только натуральные числа, но в практических расчетах за два тысячелетия до нашей эры в Древнем Египте и Древнем Вавилоне уже применялись дроби. Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел, это было сделано китайскими математиками за 2 века до нашей эры. Отрицательные числа применял в 3 веке нашей эры древнегреческий математик Диофант, знавший уже правила действий над ними, а в 7 веке нашей эры эти числа подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменение величин. Уже в 8 веке нашей эры было установлено, что квадратный корень из положительного числа имеет два значение - положительное и отрицательное, а из отрицательных чисел квадратные корни извлечь нельзя: нет такого числа х, чтобы х² = -9. В 16 веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Введение комплексных чисел было связано с открытием решения кубического уравнения, т.е. ещё в 16 веке.
До этого открытия при решении квадратного уравнения x 2 + px + q = 0 приходилось сталкиваться со случаем, когда требовалось извлечь квадратный корень из ( p /2) 2 - q , где величина ( p /2) 2 была меньше, чем q . Но в таком случае заключали, что уравнение не имеет решений. О введении новых (комплексных) чисел в это время (когда даже отрицательные числа считались “ложными”) не могло быть и мысли. Но при решении кубического уравнения по правилу Тартальи оказалось, что без действий над мнимыми числами нельзя получить действительный корень.
Теория комплексных чисел развивалась медленно: ещё в 18 веке крупнейшие математики мира спорили о том, как находить логарифмы комплексных чисел. Хотя с помощью комплексных чисел удалось получить много важных фактов, относящихся к действительным числам, но самое существование комплексных чисел многим казалось сомнительным. Исчерпывающие правила действий с комплексными числами дал и в 18 веке русский академик Эйлер – один из величайших математиков всех времён и народов. На рубеже 18 и 19 веков было указано Весселем (Дания) и Арганом (Франция) геометрическое изображение комплексных чисел. Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831 г. когда тот же способ был развит великим математиком Гауссом (Германия), он стал всеобщим достоянием.
О комплексных числах.
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они и называются комплексными.
Комплексное число имеет вид a + bi ; здесь a и b – действительные числа , а i – число нового рода, называемое мнимой единицей.
“Мнимые” числа составляют частный вид комплексных чисел (когда а = 0).
С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).
Действительное число a назовем абсциссой комплексного числа a + bi ; действительное число b – ординатой комплексного числа a + bi .
Основное свойство числа i состоит в том, что произведение i * i равно –1, т.е. i 2 = -1. (1)
Долгое время не удавалось найти такие физические величины, над которыми можно выполнять действия, подчинённые тем же правилам, что и действия над комплексными числами – в частности правилу (1). Отсюда названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен целый ряд таких физических величин, и комплексные числа широко применяются не только в математике, но также и в физике и технике.
Оставим в стороне вопрос о геометрическом или физическом смысле числа i , потому что в разных областях науки этот смысл различен.
Правило каждого действия над комплексными числами выводится из определения этого действия. Но определения действий над комплексными числами не вымышлены произвольно, а установлены с таким расчетом, чтобы согласовались с правилами действий над вещественными числами. Ведь комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними.
Соглашение о комплексных числах.
Действительное число а записывается также в виде a + 0 i (или a – 0 i ).
Запись 3 + 0 i обозначает то же, что запись 3. Запись –2 + 0 i означает –2.
Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi .
Два комплексных a + bi , a ’ + b ’ i считаются равными, если у них соответственно равны абсциссы и ординаты, т. е. Если a = a ’, b = b ’. В противном случае комплексные числа не равны. Это определение подсказывается следующим соображением. Если бы могло существовать, скажем, такое равенство:
2 + 5 i = 8 + 2 i , то по правилам алгебры мы имели бы i = 2, тогда как i не должно бать действительным числом.
З а м е ч а н и е. Мы еще не определили, что такое с л о ж е н и е комплексных чисел. Поэтому, строго говоря, мы ещё не в праве утверждать, что число 2 + 5 i есть сумма чисел 2 и 5 i . Точнее было бы сказать, что у нас есть пара действительных чисел: 2 (абсцисса) и 5 (ордината); эти числа порождают число нового рода, условно обозначаемое 5 + 7 i .
Сложение комплексных чисел
О п р е д е л е н и е. Суммой комплексных чисел a + bi и a ’ + b ’ i называют комплексное число ( a + a ’) + ( b + b ’) i .
Это определение подсказывается правилами действий с обычными многочленами.
Пример 1. (-3 + 5i) + (4 – 8i) = 1 - 3i
Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0 i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Пример 4. (-2 + 3 i ) + ( - 2 – 3 i ) = - 4
В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа a + bi и a - bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
З а м е ч а н и е. Теперь, когда действие сложения определено, мы имеем право рассматривать комплексное число a + bi как сумму чисел a и bi . Так, число 2 и число 5 i в сумме дают число 2 + 5 i .
Вычитание комплексных чисел.
О п р е д е л е н и е. Разностью комплексных чисел a + bi (уменьшаемое) и a ’ + b ’ i (вычитаемое) называется комплексное число ( a – a ’) + ( b – b ’) i .
Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
Умножение комплексных чисел.
О п р е д е л е н и е. Произведением комплексных чисел a + bi и a ’ + b ’ i
называется комплексное число
(aa’ – bb’) + (ab’ + ba’)i.
З а м е ч а н и е 1. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i 2 = -1.
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a 2 + b 2
Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.
Деление комплексных чисел.
В соответствии с определением деления действительных чисел устанавливается следующее определение.
О п р е д л е н и е. Разделить комплексное число a + bi на комплексное число a ’ + b ’ i – значит найти такое число x + yi , которое, будучи помножено на делитель, даст делимое.
Если делитель не равен нулю, то деление всегда возможно, и частное единственно. На практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4 i ) :(3 + 2i).
Записав дробь (7 – 4 i )/(3 + 2 i ), расширяем её на число 3 – 2 i , сопряженное с 3 + 2 i . Получим:
((7 – 4 i )(3 - 2 i ))/((3 + 2 i )(3 – 2 i )) = (13 – 26 i )/13 = 1 – 2 i .
Пример 1 предыдущего параграфа даёт проверку.
Пример 2. (-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)( -3 + 4i)) = (-14 –23i)/25 = -0,56 – 0.92i.
Модуль и аргумент комплексного числа.
Длина вектора, изображающего комплексное число, называется модулем этого комплексного числа. Модуль всякого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + bi обозначается | a + bi |, а также буквой r . Из чертежа видно, что
r = | a + bi | = a 2 + b 2
Модуль действительного числа совпадает с его абсолютным значением. Сопряжённые комплексные числа a + bi u a – bi имеют один и тот же модуль.
Тригонометрическая форма комплексного числа.
Абсцисса а и ордината b комплексного числа a + bi выражаются через модуль r и агрумент q . Формулами
a = r cos q; b = r sin q.
Поэтому всякое комплексное комплексное число можно представить в виде r ( cos q + i sin q ), где r > 0.
Это выражение называется нормальной тригонометрической формой или, короче, тригонометрической формой комплексного числа.
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Уже простейшие алгебраические операции над действительными числами (извлечение квадратного корня из отрицательного числа, решение квадратного уравнения с отрицательным дискриминантом) выводят за пределы множества действительных чисел. Дальнейшее обобщение понятия числа приводит к комплексным числам. Замечательным свойством множества комплексных чисел является его замкнутость относительно основных математических операций. Иначе говоря, основные математические операции над комплексными числами не выводят из множества комплексных чисел.
Комплексным числом (в алгебраической форме) называется выражение
где – произвольные действительные числа, – мнимая единица, определяемая условием .
Комплексно-сопряженным к числу называется число . Очевидно, комплексно–сопряженное число к числу совпадает с числом : .
Арифметические операции. Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры.
Пример 1. Заданы комплексные числа , .
Решение. ;
Задача 1. Пусть и – пара комплексно-сопряженных чисел. Показать, что их сумма есть действительное число, разность – мнимое число, а произведение есть действительное неотрицательное число.
Пример 2. Найти , .
Замечание. Степени числа можно представить в виде таблицы
Пример 3. Перемножить числа и .
Решение.
Пример 4. Вычислить а) ; б) ; в) .
Решение.
а) Раскроем квадрат разности:
б) Раскроем куб суммы:
Можно было считать так: .
Пример 5. Найти частное , если .
Решение.
Пример 6. Вычислить а) , б) .
Решение. а) .
Запомним:
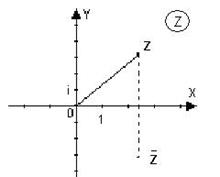
Геометрическая интерпретация комплексного числа.
Рассмотрим декартову прямоугольную систему координат. Отложим по оси абсцисс действительную часть комплексного числа , а по оси ординат – его мнимую часть . Получим точку с координатами . При этом каждому комплексному числу соответствует одна точка плоскости. Верно и обратное: каждой точке плоскости можно поставить в соответствие комплексное число , действительная часть которого равна абсциссе точки, а мнимая часть равна ординате точки. Таким образом, между комплексными числами и точками плоскости устанавливается взаимно однозначное соответствие. (Ранее мы говорили о взаимно однозначном соответствии между действительными числами и точками числовой прямой).
Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью. Для отличия её от действительной плоскости в правом верхнем углу пишут букву , обведенную кружком. Ось абсцисс на такой плоскости называют действительной осью, а ось ординат – мнимой осью. Комплексно-сопряженное число – это зеркальное отражение заданного комплексного числа относительно действительной оси. Начало координат называется нуль-точкой. Расстояние комплексного числа от начала координат называется модулем этого числа:
.
Задача 2. Доказать, что .
Модуль разности двух комплексных чисел – это расстояние между соответствующими точками:
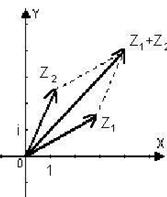
Каждой точке комплексной плоскости поставим в соответствие вектор с началом в нуль-точке и концом в данной точке. Очевидно, это соответствие взаимно однозначно. В такой интерпретации действительная и мнимая части комплексного числа – это первая и вторая компоненты вектора. Сумма представляется теперь диагональю параллелограмма, построенного на векторах и , разность понимается как . Модуль комплексного числа представляет собой длину вектора. Геометрически очевидным является неравенство треугольника в комплексной плоскости: .
Пример 7. Указать геометрическое место точек на комплексной плоскости, для которых
Решение. а) Так как , то заданное двойное неравенство можно переписать в виде: . Получили вертикальную полосу.
б) Так как , то заданное двойное неравенство перепишем в виде: . Получили горизонтальную полосу. Задачи в) и г) решить самостоятельно.
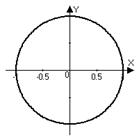
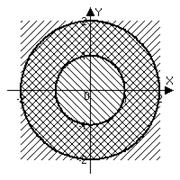
Пример 8. Указать геометрическое место точек на комплексной плоскости, для которых а) ; б) ; в) .
Решение. а) Модуль комплексного числа – это длина вектора, идущего из нуль-точки в точку , т.е. расстояние от начала координат до точки . Значит, в случае речь идет о геометрическом месте точек плоскости, равноудаленных от начала координат – это окружность (в данном случае радиус окружности равен 1). Можно было перевести задачу на язык декартовых координат:
б) Здесь речь идет о геометрическом месте точек, находящихся вне круга радиуса (с центром в начале координат).
в) точки находятся в кольце между окружностями радиуса и .
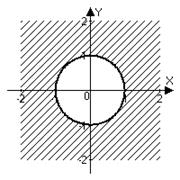
Пример 9. Указать геометрическое место точек на комплексной плоскости, для которых а) ; б) ; в) .
Решение. а) Модуль разности – это расстояние между точкой комплексной плоскости и точкой 1. Значит, речь идет о геометрическом месте точек, равноудаленных (на расстояние 1) от точки 1, – это окружность радиуса 1 с центром в точке (1;0). На языке координат:
б) Точки находятся одновременно в круге с центром в начале координат и в круге с центром, смещенным в точку : .
в) Это точки правой полуплоскости , лежащие внутри круга : .
:
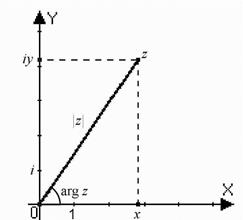
Тригонометрическая форма комплексного числа. Аргументом комплексного числа называют угол , который составляет вектор с положительным направлением действительной оси, . Этот угол определяется неоднозначно:
Здесь – главное значение аргумента, оно выделяется неравенствами (т.е. на комплексной плоскости проводится разрез по действительной оси влево от начала координат).
В первом столбце указан для числа , лежащего на действительной или мнимой оси, а во втором столбце - для всех остальных комплексных чисел.
Обозначим . Так как , , то комплексное число можно представить в тригонометрической форме:
Два комплексных числа и , заданных в тригонометрической форме
в силу неоднозначности аргумента равны тогда и только тогда, когда , .
Пример 10. Найти модули и аргументы, а также главные значения аргументов комплексных чисел . Записать каждое из них в тригонометрической форме.
Решение. Модули всех этих чисел одинаковы:
Аргумент каждого числа находим, учитывая четверть, в которой лежит соответствующая точка.
1) Точка лежит в первой четверти, значит,
В тригонометрической форме , здесь учтена - периодичность косинуса и синуса.
2) Точка лежит во второй четверти, значит,
3) Точка лежит в третьей четверти, значит,
4) Точка лежит в четвертой четверти, значит,
Умножение и деление комплексных чисел в тригонометрической форме. Пусть числа и заданы в тригонометрической форме: , . Перемножим их:
Вспоминая формулы для косинуса и синуса суммы двух углов, получаем
Для частного получаем формулу:
Пример 11. Найти произведение и частное чисел
Решение. В соответствии с формулой (1) запишем:
Проверим результат, перемножая эти числа в алгебраической форме:
По формуле (2) находим
В алгебраической форме эта операция запишется так:
Возведение комплексного числа в степень. Из формулы (1) следует, что возведение в степень комплексного числа производится по правилу
Пример 12. Вычислить 1) ; 2) .
Решение. 1) Выше мы получили запись комплексного числа в тригонометрической форме: . По формуле (3) находим . Этот же результат был получен выше в примере 4в) с помощью бинома Ньютона.
2) Прежде всего представим число в тригонометрической форме.
точка лежит в четвертой четверти, значит, . Поэтому
Остается воспользоваться формулой (3):
Раскрывая куб разности, получим тот же результат (проверьте!).
С её помощью легко получаются соотношения, выражающие синусы и косинусы кратных углов с и .
Пример 13. Выразить и через и .
Решение. Полагая в формуле Муавра , получим:
Слева раскроем куб суммы и соберем подобные члены:
Здесь учтено, что . Пришли к равенству двух комплексных чисел в алгебраической форме
которое справедливо в том и только в том случае, когда равны действительные и мнимые части этих чисел.
Равенство действительных частей дает ;
приравнивая мнимые части, получаем .
Извлечение корня из комплексного числа. Если комплексные числа и связаны соотношением , то . Представим числа и в тригонометрической форме:
Будем считать, что здесь – главное значение аргумента числа .
Наша задача – по заданному числу (т.е. по известным и ) определить (т.е. и ). В соответствии с формулой (3) равенство запишется в виде
Из равенства двух комплексных чисел в тригонометрической форме следует:
Здесь – корень -ой степени из действительного неотрицательного числа. Значит, для корня -ой степени из комплексного числа получаем формулу
Полагая последовательно , получим различных значений :
Все эти корни имеют одинаковые модули , т.е. соответствующие точки располагаются на окружности радиуса с центром в начале координат. Аргументы двух соседних корней отличаются на угол . Значит, все значения корня -ой степени из комплексного числа находятся в вершинах правильного -угольника, вписанного в окружность радиуса .
Пример 14. Найти все значения корня -ой степени из комплексного числа и изобразить их на комплексной плоскости, если
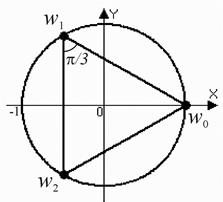
Решение. 1) Прежде всего, найдем модуль и аргумент комплексного числа : . Формула (5) для примет вид
Точки находятся в вершинах правильного треугольника, вписанного в окружность единичного радиуса, один корень – является действительным числом. Аргументы двух соседних точек отличаются на угол . Заметим, что .
2) Здесь : , поэтому
,
Точки находятся в вершинах правильного треугольника, вписанного в окружность , корень является действительным числом. Заметим, что . Сравните с результатом пр.12.2, где получили , т.е. .
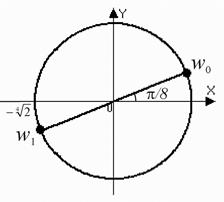
,
, откуда получаем два числа:
Запомним: .
Задача 3. Выполнить задания пр.14, если 1) , 2) .
Пример 15. Разложить на линейные множители квадратный трехчлен
Решение. 1) Рассмотрим квадратное уравнение . Его дискриминант . Значит, действительных корней нет. Из пр.14.4 следует, что . По формуле для корней квадратного уравнения . Получили два комплексно-сопряженных корня и . В соответствии с найденными корнями можем разложить квадратный трехчлен на линейные множители:
2) Рассмотрим квадратное уравнение . Его дискриминант , действительных корней нет. Из пр.14.4 следует, что . По формуле для корней квадратного уравнения . Получили два комплексно-сопряженных корня и . В соответствии с найденными корнями разлагаем квадратный трехчлен на линейные множители:
Обращаем внимание на то, что квадратное уравнение с действительными коэффициентами имеет пару комплексно сопряженных корней.
Задача 4. Убедиться, что справедливы разложения на линейные множители
Показательная форма комплексного числа. Формула Эйлера (будет доказана позже):
позволяет записать комплексное число в показательной форме:
Из формулы Эйлера и из - периодичности синуса и косинуса следует:
Пример 16. Числа записать в показательной форме.
Решение. В примере 10 нашли ,
Легко проверить справедливость соотношений:
Сравните эти соотношения с правилами умножения, деления и возведения в степень комплексных чисел в тригонометрической форме.
Пример 17. Сравните комплексные числа и .
Решение. Из пр.16: . У чисел и модули равны. Выделяя в показателе числа слагаемое, кратное , представим в виде , так как множитель . Значит, .

ГОСТ
Над комплексными числами можно выполнять следующие действия:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение комплексного числа в степень;
- извлечение корня $n$--й степени из комплексного числа.
Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.
Извлечение корня выполняется для чисел, представленных в тригонометрической форме.
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ - вещественная (действительная) часть;
- $b$ - мнимая часть.
Запись некоторого комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ - модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt +b^ > $, $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac $.
Запись некоторого комплексного числа $z$ в виде $z=r\cdot e^ $ называется показательной формой записи, где число $r$ - модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt +b^ > $, $\varphi $ - аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac $.
При необходимости извлечения корня из комплексного числа, записанного в показательной форме, необходимо предварительно привести его к тригонометрической форме представления.
Готовые работы на аналогичную тему
Сумма комплексных чисел
Суммой двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое определяется равенством \[z_ +z_ =(a_ +b_ i)+(a_ +b_ i)=(a_ +a_ )+(b_ +b_ )\cdot i.\]
Разность комплексных чисел
Разностью двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое определяется равенством \[z_ -z_ =(a_ +b_ i)-(a_ +b_ i)=(a_ -a_ )+(b_ -b_ )\cdot i.\]
Выполнить действия: 1) $z_ +z_ $2) $z_ -z_ $ для заданных комплексных чисел $z_ =2+4i$ и $z_ =1-3i$.
1) По определению имеем: $z_ +z_ =(a_ +a_ )+(b_ +b_ )\cdot i$
Для исходных чисел получаем:
2) По определению имеем: $z_ -z_ =(a_ -a_ )+(b_ -b_ )\cdot i$
Для исходных чисел получаем:
Произведение комплексных чисел
Произведением двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^ =-1$.
Произведением двух заданных комплексных чисел $z_ =r_ \cdot (\cos \varphi _ +i\sin \varphi _ )$ и $z_ =r_ \cdot (\cos \varphi _ +i\sin \varphi _ )$ является комплексное число, которое определяется равенством
\[z_ \cdot z_ =r_ \cdot r_ \cdot [\cos (\varphi _ +\varphi _ )+i\sin (\varphi _ +\varphi _ )].\]
Выполнить умножение комплексных чисел представленных в алгебраической форме:
Для исходных чисел, учитывая определение, получаем:
\[1\cdot 2+3\cdot 2i+1\cdot (-2i)+3i\cdot (-2i)=2+6i-2i-6i^ =2+4i+6=8+4i\]
Выполнить умножение комплексных чисел представленных в тригонометрической форме:
$z_ =3\sqrt \cdot (\cos \frac<\pi > +i\cdot \sin \frac<\pi > )$ и $z_ =2\cdot (\cos \pi +i\cdot \sin \pi )$.
1) По определению имеем: $z_ \cdot z_ =r_ \cdot r_ \cdot [\cos (\varphi _ +\varphi _ )+i\sin (\varphi _ +\varphi _ )]$
Для исходных чисел получаем:
\[\begin \cdot z_ =\left(3\sqrt \cdot (\cos \frac<\pi > +i\cdot \sin \frac<\pi > )\right)\cdot \left(2\cdot (\cos \pi +i \cdot \sin \pi )\right)=6\cdot \sqrt \cdot \left[\cos \left(\frac<\pi > +\pi \right)+i\cdot \sin \left(\frac<\pi > +\pi \right)\right]=> \\ <=6\sqrt\cdot \left(\cos \frac<3\pi > +i\cdot \sin \frac<3\pi > \right)> \end\]
Частное комплексных чисел
Частным двух заданных комплексных чисел $z_ =r_ \cdot (\cos \varphi _ +i\sin \varphi _ )$ и $z_ =r_ \cdot (\cos \varphi _ +i \sin \varphi _ )$ является комплексное число, которое определяется равенством
\[z_ \div z_ =\frac
Чтобы выполнить операцию деления комплексных чисел, представленных в алгебраической форме, необходимо:
- представить запись операции деления в виде дроби;
- числитель и знаменатель дроби умножить на число сопряженное знаменателю;
- привести полученное выражение к алгебраической записи.
Выполнить деление комплексных чисел, представленных в алгебраической форме:
Для исходных чисел получаем:
Выполнить деление комплексных чисел представленных в тригонометрической форме:
$z_ =3\cdot \left(\cos \frac<2\pi > +i\cdot \sin \frac<2\pi > \right)$ и $z_ =2\cdot (\cos 2\pi +i\cdot \sin 2\pi )$.
По определению имеем: $z_ \div z_ =\frac
Для исходных чисел получаем:
\[\begin > > =3\cdot \left(\cos \frac<2\pi > +i\cdot \sin \frac<2\pi > \right)\div \left(2\cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)=\frac \cdot \left[\cos \left(\frac<2\pi > -2\pi \right)+i\cdot \sin \left(\frac<2\pi > -2\pi \right)\right]=> \\ <= \frac \cdot \left(\cos \left(-\frac<4\pi > \right)+i\cdot \sin \left(-\frac<4\pi > \right)\right)> \end\]
Степерь комплексного числа
Степенью порядка $n$ некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[z^ =r^ \cdot (\cos n\varphi +i\sin n\varphi ).\]
Данная формула называется формулой Муавра.
Выполнить действие $z^ $, где $z=3\cdot \left(\cos \frac<\pi > +i\cdot \sin \frac<\pi > \right)$.
По формуле Муавра получим:
\[z^ =3^ \cdot \left(\cos \left(3\cdot \frac<\pi > \right)+i\cdot \sin \left(3\cdot \frac<\pi > \right)\right)=27\cdot \left(\cos \frac <3\pi > +i\cdot \sin \frac<3\pi > \right).\]
Выполнить действие $z^ $, где $z=1\cdot \left(\cos \frac<\pi > +i\cdot \sin \frac<\pi > \right)$.
По формуле Муавра получим:
\[z^ =1^ \cdot \left(\cos \left(100\cdot \frac<\pi > \right)+i\cdot \sin \left(100\cdot \frac<\pi > \right)\right)=1\cdot \left(\cos 50\pi +i\cdot \sin 50\pi \right)=1\cdot \left(\cos 0+i\cdot \sin 0\right).\]
Корень комплексного числа
Корнем $n$-й степени некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
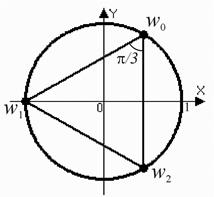
Выполнить действие $\sqrt[] $, где $z=4\cdot (\cos \pi +i\cdot \sin \pi )$.
Для $k=0$ получаем: $w_ =\sqrt[] =\sqrt[] \cdot \left(\cos \frac<\pi > +i\cdot \sin \frac<\pi > \right)$.
Для $k=1$ получаем: $w_ =\sqrt[] =\sqrt[] \cdot \left(\cos \frac<\pi +2\pi > +i\cdot \sin \frac<\pi +2\pi > \right)=\sqrt[] \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.
Для $k=2$ получаем: $w_ =\sqrt[] =\sqrt[] \cdot \left(\cos \frac<\pi +4\pi > +i\cdot \sin \frac<\pi +4\pi > \right)=\sqrt[] \cdot \left(\cos \frac<5\pi > +i\cdot \sin \frac<5\pi > \right)$.
Читайте также:

