Аналогии между поступательным и вращательным движением доклад

Обновлено: 04.07.2024

Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ, линейной скорости
v – угловая скорость w, линейному (касательному) ускорению а – угловое ускорение ε.

Поступательное движение	Вращательное движение
Кинематические характеристики движения
Путь	S	м	Угол поворота	j	рад
Время	t	с	Период	Т	с
Скорость	v	м/с	Угловая скорость	w	рад/с
Ускорение	a	м/с 2	Угловое ускорение	e	рад/с 2
Поступательное движение	Вращательное движение
Динамическиехарактеристики движения
Масса	m	кг	Момент инерции	J	кг × м 2
Сила	F	Н	Момент силы	M	Н×м
Импульс	p	кг ×м/с	Момент импульса	L=J×w	кг ×м 2 /с
Второй закон Ньютона	F=ma; F=dp/dt	Уравнение динамики вращательного движения	M=J×e; M=dL/dt
Работа	dA=F× dS	Дж	Работа	dA=M×dj	Дж
Кинетическая энергия	E_K=(mv 2 )/2	Дж	Кинетическая энергия	E_KВР=(Jw 2 )/2	Дж
Мощность	N=FV	Вт	Мощность	N=М×w	Вт

Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.

Момент инерции материальной точки и тела. Примеры вычисления момента инерции (цилиндр, шар).

Моментом инерции материальной точки относительно оси называется величина, равная произведению массы точки на квадрат расстояния до рассматриваемой оси: .

Единица момента инерции - килограмм-метр в квадрате ( ). Моментом инерции твердого тела называют сумму моментов инерции материальных точек массой , на которые можно разделить это тело, т. е. .

Переходя к бесконечно малым массам dm, получаем

На основании этой формулы можно рассчитать момент инерции любого тела.

В качестве примера получим формулу момента инерции однородного сплошного цилиндра относительно его оси (рис. 1).

Разобьем цилиндр на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии r от оси. Объем такого слоя

, где h – высота цилиндра.

Поскольку цилиндр однороден, то масса dm выделенного слоя

, где r - плотность тела.

Так как - объем цилиндра, а - его масса, формулу приводим к виду . Эта формула применима для цилиндра любой высоты, в том числе и для диска.

Аналогично можно рассчитать моменты инерции и других однородных тел:

- для полого тонкостенного цилиндра относительно оси симметрии , где R - радиус цилиндра;

- для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его середину, , где l - длина стержня;

- для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его конец, , где l - длина стержня;

- для шара относительно оси симметрии , где R - радиус шара.

При нахождении момента инерции тел относительно оси, не проходящей через центр масс тела, вычисления значительно усложняются. Однако в подобных случаях можно воспользоваться теоремой Штейнера, которая формулируется следующим образом: момент инерции I относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями: .

Момент инерции твердого тела является мерой его инертности при вращательном движении.

Теорема Штейнера.

Теорема Штейнера применяется для установления связи между моментом инерции тел относительно двух параллельных осей .

Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

— известный момент инерции относительно оси, проходящей через центр масс тела,

— искомый момент инерции относительно параллельной оси,

— масса тела,

— расстояние между указанными осями.

Вывод теоремы

Момент инерции, по определению:

Радиус-вектор можно расписать как разность двух векторов:

где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

Вынося за сумму , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Откуда и следует искомая формула:

где — известный момент инерции относительно оси, проходящей через центр масс тела.

Пример применения

Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью ) равен

Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен

где — расстояние между искомой осью и осью . В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формуле :

Пересчёт тензора инерции

Теорема Гюйнеса — Штейнера допускает обобщение на тензор момента инерции, что позволяет получать тензор относительно произвольной точки из тензора относительно центра масс. Пусть — смещение от центра масс, тогда

— вектор смещения от центра масс, а — символ Кронекера.

16. Кинетическая энергия вращающегося тела.

Кинетическая энергия - величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно мысленно разбить:

Если тело вращается вокруг неподвижной оси z с угловой скоростью ω, то линейная скорость i-й точки vi = ωRi, R, - расстояние до оси. Следовательно:

Сопоставив формулы, можно увидеть, что момент инерции тела J является мерой инертности при вращательном движении, так же как масса m - мера инерции при поступательном движении.

В общем случае движение тввердого тела можно представить в виде суммы двух движений – поступательного со скоростью ύ_c и вращательного с угловой скоростью ὡ вокруг мгновенной оси, проходящей через центр инерции этого тела

К_полн. =

Здесь - момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.

17. Гироскоп. Гироскопический эффект. Прецессия гироскопа

Гироскоп – прибор, имеющий свободную ось вращения и способный реагировать на изменение углов ориентации тела, на котором он установлен. При вращении гироскоп сохраняет свое положение неизменным. Гироскопы представляют собой вращающиеся с высокой частотой твердые тела. Ось вращения гироскопа может изменять свое направление в пространстве. Свойствами гироскопа обладают вращающиеся артиллерийские снаряды, винты самолетов, роторы турбин. Простейший пример гироскопа – волчок или хорошо всем известная детская игрушка юла. Тело, вращающееся вокруг определенной оси, которая сохраняет положение в пространстве, если на гироскоп не действуют какие-то внешние силы и моменты этих сил. При этом гироскоп обладает устойчивостью и способен противостоять воздействию внешней силы, что во многом определяется его скоростью вращения. Например, если мы быстро раскрутим юлу, а потом толкнем ее, она не упадет, а продолжит вращение. А когда скорость волчка упадет до определенного значения, начнется прецессия – явление, когда ось вращения описывает конус, а момент импульса волчка меняет направление в пространстве.

Гироскопическим эффектом называется явление сохранения неизменности своего направления в пространстве быстровращающимся осесимметричным твердым телом.

Гироскопический эффект свойственен небесным телам, артиллерийским снарядам, роторам турбин, устанавливаемых на судах, винтам самолетов и т.п.

Прецессия гироскопа

Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве.

Если к оси шарнирно закрепленного в точке О гироскопа (рис. 92) прикрепить пружину и тянуть за нее вверх с силой F, то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.

Рис.92

Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы (рис.92), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением и ее плеча относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных и .

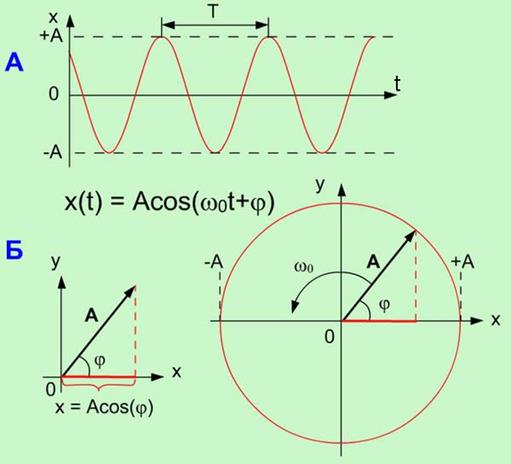
Гармонические колебания (механические) и их характеристики. Дифференциальное уравнение гармонических колебаний. Связь вращения и колебаний. Уравнение колебаний в комплексной форме.

Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.

₀ ),

где x – смещение колеблющейся величины от положения равновесия;

А – амплитуда колебаний; = 2 /Е = 2 – круговая (циклическая) частота;

v = 1| T – частота; T – период колебаний; ₀- начальная фаза ; ₀- фаза колебаний в момент t.

Круговая частота колебаний

где v и T - частота и период колебаний.

Дифференциальное уравнение гармонических колебаний материальной точки:

или + 2 x = 0,

где m - масса точки; k - коэффициент квазиупругой силы ( k = m 2 ).

Механика – наука о движении тел и взаимодействии между ними. Любые, самые сложные движения тел можно представить в виде суммы простейших движений – поступательных и вращательных. Рассмотрим определение поступательного и вращательного движения, а также их особенности.

Поступательное и вращательное движение

При решении задачи описания механического движения твердого тела достаточно часто выясняется, что все его точки движутся по одинаковым траекториям, или разницей между движением различных точек можно пренебречь. Например, при свободном падении тела траектории всех его точек будут представлять прямые линии, направленные вниз. Если мы рассмотрим годовое вращение Земли вокруг Солнца, то, в связи с суточным вращением разные точки Земного шара будут иметь немного различные траектории, однако этой разницей в абсолютном большинстве случаев можно пренебречь и описывать движение Земли как одной материальной точки.

Движение, при котором все точки твердого тела движутся по одинаковым траекториям, или разницей в траекториях можно пренебречь, называется поступательным.

Рис. 1. Поступательное движение.

Другой вариант движения – это движение, при котором траектории точек тела различны. Поскольку тело твердое (то есть, взаимное расположение точек тела не меняется), разница траекторий означает, что тело меняет свое положение в пространстве. Такое движение может быть достаточно сложным, однако, его всегда можно представить, как сумму движений, при котором траектории точек тела представляют собой дуги окружностей.

Движение, при котором траектории точек тела представляют собой окружности или дуги окружностей (или отклонением от этих дуг можно пренебречь), называется вращательным. Примерами вращательного движения является движение колес и шестерен машин и механизмов, вращение Земли и других небесных тел, а также многое другое.

Рис. 2. Вращательное движение.

Общее и различие

При решении задач механики необходимо четко представлять, в чем схожесть и различие между поступательным и вращательным движениями.

Общие черты заключаются в самом понятии движения. Поступательное и вращательное движение твердого тела – это изменение координат точек тела с течением времени. Независимо от вида движений все точки тела всегда имеют некоторые координаты в Системе Отсчета, некоторую скорость и некоторое ускорение.

Параметры поступательного и вращательного движений неодинаковы, но аналогичны. Вместо координаты для описания вращения используется угол поворота, скорость и ускорение для вращения являются угловыми.

Однако, если поступательное движение описывается относительно только принятых координатных осей, то для вращательного движения учитывается еще одна ось, относительно которой совершается вращение. Следствием этого является необходимость учитывать расстояние до этой оси (радиус вращения), а также невозможность описания вращательного движения с помощью только одной координаты. Вращение всегда требует двух или трех координат.

Еще одна особенность вращательного движения – невозможность движения без ускорения. Даже если вращение происходит с постоянной угловой скоростью, и угловое ускорение равно нулю, мгновенная скорость материальной точки постоянно меняет направление, а значит, такое движение происходит с ускорением, которое называется центростремительным.

Рис. 3. Аналогия величин для поступательного и вращательного движения.

Что мы узнали?

Любые движения тел могут быть описаны суммой простейших поступательных и вращательных движений. Поступательное движение – это движение, при котором траектории всех точек тела одинаковы. Вращательное движение – это движение, при котором траектории точек тела представляют собой окружности (или дуги окружностей) с центрами, лежащими на одной прямой (в одной точке для двумерного случая).

Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.

Поступательное криволинейное движение. Угол поворота тела

Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.

Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.

Рисунок 1 . Поступательное криволинейное движение кабин колеса обзора

Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.

Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.

Если имеется поступательное движение, то общая скорость для всех точек тела υ → называется скоростью поступательного движения, а ускорение a → - ускорением поступательного движения. Изображение векторов υ → и a → принято указывать приложенными в любой точке тела.

Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.

Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.

Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось A z , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2 .

Рисунок 2 . Угол поворота тела

Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t , то есть φ = f ( t ) . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.

При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.

Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε .

Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ , скорость υ на угловую скорость ω , а ускорение a на угловое ε .

Вращательное и поступательное движение. Формулы

Поступательное	Вращательное
Равномерное
s = υ · t	φ = ω · t
υ = c o n s t	ω = c o n s t
a = 0	ε = 0
Равнопеременное
s = υ 0 t ± a t 2 2	φ = ω 0 t ± ε · t 2 2
υ = υ 0 ± a · t	ω = ω 0 ± ε · t
a = c o n s t	ε = c o n s t
Неравномерное
s = f ( t )	φ = f ( t )
υ = d s d t	ω = d φ d t
a = d υ d t = d 2 s d t 2	ε = d ω d t = d 2 φ d t 2

Задачи на вращательное движение

Дана материальная точка, которая движется прямолинейно соответственно уравнению s = t 4 + 2 t 2 + 5 . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.

Дано: s = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: s ; υ ; υ ; α .

Решение

s = 2 4 + 2 · 2 2 + 5 = 29 м .

υ = d s d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 м / с .

υ = ∆ s ∆ t = 29 2 = 14 , 5 м / с .

a = d υ d t = 12 t 2 + 4 = 12 · 2 2 + 4 = 52 м / с 2 .

Ответ: s = 29 м ; υ = 37 м / с ; υ = 14 , 5 м / с ; α = 52 м / с 2

Задано тело, вращающееся вокруг неподвижной оси по уравнению φ = t 4 + 2 t 2 + 5 . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.

Дано: φ = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: φ ; ω ; ω ; ε .

Решение

φ = 2 4 + 2 · 2 2 + 5 = 29 р а д .

ω = d φ d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 р а д / с .

ω = ∆ φ ∆ t = 29 2 = 14 , 5 р а д / с .

ε = d ω d t = 12 2 + 4 = 12 · 2 2 + 4 = 52 р а д / с 2 .

Ответ: φ = 29 р а д ; ω = 37 р а д / с ; ω = 14 , 5 р а д / с ; ε = 52 р а д / с 2 .

6. Дифференциальные и кинематические уравнения колебаний. Маятники. Параметры колебания

Дифференциальные уравнения колебаний

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

· Уравнение гармонических колебаний

где – смещение точки от положения равновесия, А – амплитуда колебаний, - фаза колебаний, w₀– круговая (циклическая частота), t – время, – начальная фаза колебаний.

где – частота колебаний, – период колебаний.

· Скорость и ускорение при гармонических колебаниях

- амплитуда скорости (максимальное значение);

- амплитуда ускорения (максимальное значение).

При графики зависимостей представлены на рис. 1(а,б,в), соответственно.

где – коэффициент упругой (квазиупругой) силы, m – масса материальной точки;

- амплитуда силы (максимальное значение).

· Кинетическая энергия колеблющейся точки

-амплитуда кинетической энергии (максимальное значение).

· Потенциальная энергия колеблющейся точки

-амплитуда потенциальной энергии (максимальное значение).

При графики зависимостей кинетической и потенциальной энергии от времени представлены на рис. 2а и 2б, соответственно.

· Полная энергия при гармонических колебаниях (рис. 2в)

· Уравнения гармонических колебаний могут быть заданы функциями синуса или косинуса. В таблице 1 даны значения скорости, ускорения, силы и энергии в обоих случаях.

– математический маятник ( – длина нити);

– пружинный маятник (m – масса тела, – коэффициент жесткости);

– физический маятник ( – момент инерции тела относительно оси, проходящей через точку подвеса, определяется по теореме Штейнера, m – масса тела, d – расстояние от точки подвеса до центра масс).

Пример: Однородный диск радиусом колеблется около горизонтальной оси, проходящей на расстоянии от центра диска. Определить период колебаний диска относительно этой оси (рис. 3).

Период определяется по формуле , где (нашли по теореме Штейнера). Тогда

· Уравнение затухающих колебаний (рис. 4)

где – амплитуда колебаний в начальный момент времени, – коэффициент затухания, - зависимость амплитуды затухающих колебаний от времени, -частота затухающих колебаний, - частота собственных колебаний, - период затухающих колебаний.

· Уравнение вынужденных колебаний, совершаемых под действием периодически изменяющейся силы

- амплитуда вынужденных колебаний;

- начальная фаза вынужденных колебаний;

и - частоты собственных и вынужденных колебаний .

· Резонанс – резкое возрастание амплитуды вынужденных колебаний при частоте, близкой к частоте собственных колебаний.

· Амплитуда при резонансе

Примеры решений задач по астрономии: Фокусное расстояние объектива телескопа составляет 900 мм, а фокусное .

Историческое сочинение по периоду истории с 1019-1054 г.: Все эти процессы связаны с деятельностью таких личностей, как.

Читайте также: