Алгебраические дроби доклад 5 класс

Обновлено: 05.07.2024

После полученных начальных сведений о дробях перейдем к действиям с алгебраическими дробями. С ними можно выполнять любые действия вплоть до возведения в степень. При их выполнении мы в итоге получаем алгебраическую дробь. Все пункты необходимо разбирать последовательно.

Действия с алгебраическими дробями аналогичны действиям с обыкновенными дробями. Поэтому стоит отметить, что правила являются совпадающими при любых выполняемых с ними действиями.

Сложение алгебраических дробей

Сложение может выполняться в двух случаях: при одинаковых знаменателях, при наличии разных знаменателей.

Если необходимо произвести сложение дробей с одинаковыми знаменателями, нужно сложить числители, а знаменатель оставить без изменения. Это правило позволяет воспользоваться сложением дробей и многочленов, которые находятся в числителях. Получим, что

a 2 + a · b a · b - 5 + 2 · a · b + 3 a · b - 5 + 2 · b 4 - 4 a · b - 5 = a 2 + a · b + 2 · a · b + 3 + 2 · b 4 - 4 a · b - 5 = = a 2 + 3 · a · b - 1 + 2 · b 4 a · b - 5

Если имеются числители дроби с разными числителями, тогда необходимо применить правило: воспользоваться приведением к общему знаменателю, выполнить сложение полученных дробей.

Нужно произвести сложение дробей x x 2 - 1 и 3 x 2 - x

Решение

Приводим к общему знаменателю вида x 2 x · x - 1 · x + 1 и 3 · x + 3 x · ( x - 1 ) · ( x + 1 ) .

Выполним сложение и получим, что

x 2 x · ( x - 1 ) · ( x + 1 ) + 3 · x + 3 x · ( x - 1 ) · ( x + 1 ) = x 2 + 3 · x + 3 x · ( x - 1 ) · ( x + 1 ) = x 2 + 3 · x + 3 x 3 - x

Ответ: x 2 + 3 · x + 3 x 3 - x

Статья о сложении и вычитании таких дробей имеет подробную информацию, где подробно описано каждое действие, производимое над дробями. При выполнении сложения возможно появление сократимой дроби.

Вычитание

Вычитание выполняется аналогично сложению. При одинаковых знаменателях действия выполняются только в числителе, знаменатель остается неизменным. При различных знаменателях выполняется приведение к общему. Только после этого можно приступать к вычислениям.

Перейдем к вычитанию дробей a + 5 a 2 + 2 и 1 - 2 · a 2 + a a 2 + 2 .

Решение

Видно, что знаменатели идентичны, что означает a + 5 a 2 + 2 - 1 - 2 · a 2 + a a 2 + 2 = a + 5 - ( 1 - 2 · a 2 + a ) a 2 + 2 = 2 · a 2 + 4 a 2 + 2 .

Произведем сокращение дроби 2 · a 2 + 4 a 2 + 2 = 2 · a 2 + 2 a 2 + 2 = 2 .

Ответ: 2

Выполним вычитание 4 5 · x и 3 x - 1 .

Решение

Знаменатели разные, поэтому приведем к общему 5 · x · ( x - 1 ) , получаем 4 5 · x = 4 · x - 1 5 · x · ( x - 1 ) = 4 · x - 4 5 · x · ( x - 1 ) и 3 x - 1 = 3 · 5 · x ( x - 1 ) · 5 · x = 15 · x 5 · x · ( x - 1 ) .

4 5 · x - 3 x - 1 = 4 · x - 4 5 · x · ( x - 1 ) - 15 · x 5 · x · ( x - 1 ) = 4 · x - 4 - 15 · x 5 · x · ( x - 1 ) = = - 4 - 11 · x 5 · x · ( x - 1 ) = - 4 - 11 · x 5 · x 2 - 5 · x

Ответ: - 4 - 11 · x 5 · x 2 - 5 · x

Детальная информация указана в статье о сложении и вычитании алгебраических дробей.

Умножение алгебраических дробей

С дробями можно производить умножение аналогичное умножению обыкновенных дробей: для того, чтобы умножить дроби, необходимо произвести умножение числителей и знаменателей отдельно.

Рассмотрим пример такого плана.

При умножении 2 x + 2 на x - x · y y из правила получаем, что 2 x + 2 · x - x · y y = 2 · ( x - x · y ) ( x + 2 ) · y .

Теперь необходимо выполнить преобразования, то есть умножить одночлен на многочлен. Получаем, что

2 · x - x · y ( x + 2 ) · y = 2 · x - 2 · x · y x · y + 2 · y

Предварительно следует произвести разложение дроби на многочлены для того, чтобы упростить дробь. После можно производить сокращение. Имеем, что

2 · x 3 - 8 · x 3 · x · y - y · 6 · y 5 x 2 + 2 · x = 2 · x · ( x - 2 ) · ( x + 2 ) y · ( 3 · x - 1 ) · 6 · y 5 x · ( x + 2 ) = = 2 · x · ( x - 2 ) · ( x + 2 ) · 6 · y 5 y · ( 3 · x - 1 ) · x · x + 2 = 12 · ( x - 2 ) · y 4 3 · x - 1 = 12 · x · y 4 - 24 · y 4 3 · x - 1

Подробное рассмотрение данного действия можно найти в статье умножения и деления дробей.

Деление

Рассмотрим деление с алгебраическими дробями. Применим правило: для того, чтобы разделить дроби, необходимо первую умножить на обратную вторую.

Дробь, которая обратная данной считается дробь с поменянными местами числителем и знаменателем. То есть, эта дробь называется взаимообратной.

Выполнить деление x 2 - x · y 9 · y 2 : 2 · x 3 · y .

Решение

Тогда обратная 2 · x 3 · y дробь запишется как 3 · y 2 · x . Значит, получим, что x 2 - x · y 9 · y 2 : 2 · x 3 · y = x 2 - x · y 9 · y 2 · 3 · y 2 · x = x · x - y · 3 · y 9 · y 2 · 2 · x = x - y 6 · y .

Ответ: x 2 - x · y 9 · y 2 : 2 · x 3 · y = x - y 6 · y

Возведение алгебраической дроби в степень

Если имеется натуральная степень, тогда необходимо применять правило действий с возведением в натуральную степень. При таких вычислениях используем правило: при возведении в степень нужно числитель и знаменатель отдельно возводить в степени, после чего записать результат.

Рассмотрим на примере дроби 2 · x x - y . Если необходимо возвести ее в степень равную 2 , тогда выполняем действия : 2 · x x - y 2 = 2 · x 2 ( x - y ) 2 . После чего возводим в степень получившийся одночлен. Выполнив действия, получим, что дроби примет вид 4 · x 2 x 2 - 2 · x · y + y 2 .

Детальное решение подобных примеров рассматривается в статье про возведение алгебраической дроби в степень.

Прежде чем перейти к изучению алгебраических дробей рекомендуем вспомнить, как работать с обыкновенными дробями.

Запомните!

Любая дробь, в которой есть буквенный множитель, называется алгебраической дробью.

Примеры алгебраических дробей.

Как и у обыкновенной дроби, в алгебраической дроби есть числитель (наверху) и знаменатель (внизу).

Сокращение алгебраической дроби

Алгебраическую дробь можно сокращать. При сокращении пользуются правилами сокращения обыкновенных дробей.

Напоминаем, что при сокращении обыкновенной дроби мы делили и числитель, и знаменатель на одно и тоже число.

Алгебраическую дробь сокращают таким же образом, но только числитель и знаменатель делят на один и тот же многочлен.

Рассмотрим пример сокращения алгебраической дроби.

Напоминаем, что любая буква или число в нулевой степени — это единица.

Нет необходимости каждый раз подробно записывать, на что сокращали алгебраическую дробь. Достаточно держать в уме степень, на которую сокращали, и записывать только результат.

Краткая запись сокращения алгебраической дроби выглядит следующим образом.

Важно!

Сокращать можно только одинаковые буквенные множители.

Нельзя сокращать

Можно сокращать

Другие примеры сокращения алгебраических дробей.

Как сократить дробь с многочленами

Рассмотрим другой пример алгебраической дроби. Требуется сократить алгебраическую дробь, у которой в числителе стоит многочлен.

Важно!

Сокращать многочлен в скобках можно только с точно таким же многочленом в скобках!

Ни в коем случае нельзя сокращать часть многочлена внутри скобок!

Неправильно

Правильно

Определить, где заканчивается многочлен, очень просто. Между многочленами может быть только знак умножения. Весь многочлен находится внутри скобок.

Примеры сокращения алгебраических дробей с многочленами.

Вынесение общего множителя при сокращении дробей

Чтобы в алгебраических дробях появились одинаковые многочлены иногда нужно вынести общий множитель за скобки.

Сокращение дробей с помощью формул сокращенного умножения

В других примерах для сокращения алгебраических дробей требуется
применение формул сокращенного умножения.

В первоначальном виде сократить алгебраическую дробь нельзя, так как нет одинаковых многочленов.

Другие примеры сокращения алгебраических дробей с помощью формул сокращенного умножения.

Ключевые слова конспекта: алгебраические дроби, основное свойство дроби, сокращение дробей.

Алгебраической называют дробь, в числителе и (или) знаменателе которой стоят алгебраические выражения. Например:

Если в эти выражения вместо букв подставить их числовые значения, то в числителе и знаменателе алгебраической дроби получатся числа, и дробь превратится в обыкновенную. А раз так, то алгебраическая дробь обладает всеми свойствами обыкновенной дроби, в частности основным свойством дроби:

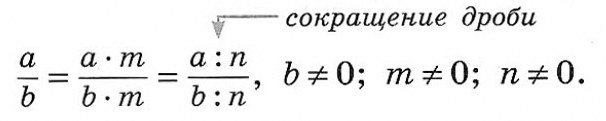
Величина дроби не изменится, если её числитель и знаменатель одновременно умножить или разделить на одно и то же число или алгебраическое выражение, не равное нулю.

Так как на нуль делить нельзя, то сразу договоримся, что знаменатели всех рассматриваемых нами дробей не равны нулю, то есть переменные, из которых состоят знаменатели, принимают только допустимые значения.

Сокращение дробей

сократить коэффициенты;
перебрать по очереди все буквы, деля числитель и знаменатель на букву в наименьшей степени (здесь разделили на а 2 и на b).

Алгебраические выражения в числителе и знаменателе разложим на множители, полученную дробь сократим:

Заметим, что
(а — b) : (а — b) = 1 и (b — а) : (а — b) = — (а — b) : (а — b) = — 1 , поэтому

Помни: (а — b) 2 = (b — а) 2 .

Слайд 2

Слайд 3

Что такое алгебраическая дробь? ⁮Запись , в которой а – число или выражение, а b – выражение с переменной, называется рациональной (алгебраической) дробью. Пример:

Слайд 4

Основное свойство алгебраической дроби – числитель и знаменатель алгебраической дроби можно умножать (делить) на одно и то же число, не равное нулю. Основное свойство алгебраической дроби – числитель и знаменатель алгебраической дроби можно умножать (делить) на одно и то же число, не равное нулю.

Слайд 5

Допустимые значения переменных (ОДЗ) – такие значения переменных, при которых выражение имеет смысл (т. е. знаменатель не равен нулю). Допустимые значения переменных (ОДЗ) – такие значения переменных, при которых выражение имеет смысл (т. е. знаменатель не равен нулю). Пример 1: , Допустимые значения переменной y:

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Сокращение дробей Чтобы сократить дробь, необходимо числитель и знаменатель данной дроби разложить на множители и сократить на общий множитель. Пример 1:

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Сложение и вычитание дробей с одинаковыми знаменателями Чтобы сложить (вычесть) дроби с одинаковыми знаменателями, нужно знаменатели оставить без изменения, а числители сложить (вычесть). Примеры:

Слайд 14

Слайд 15

Сложение и вычитание дробей с разными знаменателями Чтобы сложить (вычесть) дроби с разными знаменателями, нужно: Разложить знаменатели дробей на множители; Привести дроби к общему знаменателю; Сложить (вычесть) числители, а знаменатели оставить без изменения.

Слайд 16

Слайд 17

Слайд 18

Умножение дробей Произведение двух дробей равно дроби, числитель которой равен произведению числителей этих дробей, а знаменатель – произведению знаменателей.

Слайд 19

Слайд 20

Слайд 21

Деление дробей Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.

Слайд 22

Слайд 23

Слайд 24

Возведение дроби в степень Чтобы возвести дробь в степень n, нужно возвести и числитель, и знаменатель в степень n.

Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Читайте также: