Аксиоматический метод презентация и доклад

Обновлено: 25.06.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Система Евклида явилась первым опытом применения аксиоматического метода и просуществовала без изменений до XIX века н. э. Однако она обладала рядом недостатков с современной точки зрения на аксиоматический метод, и на рубеже XIX–XX веков была построена геометрическая система, свободная от этих недостатков. Историческая справка

Суть аксиоматического метода построения научной теории состоит в следующем: перечисляются основные (неопределяемые) понятия, все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее. Суть метода

Основные понятия делятся на два вида: одни обозначают объекты, которыми занимается теория, другие обозначают отношения между ними. Так, точка и прямая – это объекты геометрии, а то, что точка принадлежит прямой, – отношение между ними. Основные понятия

Необходимость введения основных понятий очевидна, так как процесс, состоящий в том, чтобы определить одни объекты через другие, более простые, а эти в свою очередь через еще более простые, не будет ограничен до тех пор, пока некоторые объекты не будут считаться неопределимыми. Основные понятия

Аксиомы – предложения, принимаемые без доказательства. Доказывая какое-либо утверждение, опираются на некоторые предпосылки, которые считаются известными. Но эти предпосылки необходимо в свою очередь обосновать, опираясь на другие, и т. д. Чтобы оборвать эту бесконечную последовательность, вводят аксиомы – предпосылки, которые принимаются за исходные и составляют основу для доказательства теорем. Все остальные предложения должны являться логическим следствием аксиом или ранее доказанных утверждений. Список основных понятий и формулировки аксиом составляет основу теории и, в частности, планиметрии. Необходимо отметить, что основные понятия и аксиомы (назовем их кратко системой) вовсе не обязательно имеют отношение к окружающему нас реальному миру (пример такой системы – система неевклидовой геометрии). Они являются основой абстрактной теории, которая выводится как логическое их следствие, безотносительно к тому, верна исходная система или нет с нашей точки зрения. Аксиомы предпосылки, которые принимаются за исходные

Для того чтобы абстрактная теория приобрела определенный смысл, необходимо найти объект-модель, т.е. указать систему конкретных объектов и отношений между ними так, чтобы соблюдались установленные аксиомы. Такую модель иначе называют еще интерпретацией аксиоматики. Таким образом, изучаемая нами геометрия является моделью утвержденной ранее системы, в которой точку мы представляем как идеализацию следа остро отточенного карандаша, прямую – как идеализацию туго натянутой нити, а плоскость – как идеализацию гладкой поверхности стола. Геометрия модель аксиоматической системы

Для отвлеченной аксиоматики неизвестно, могут ли выводы из нее привести к противоречию. Такая аксиоматика, заключающая в себе противоречие, заведомо не может реализоваться и не имеет смысла. Таким образом, первое условие для любой системы аксиом – это ее непротиворечивость. Вопрос о противоречивости системы решается представлением ее модели. Непротеворечивость системы аксиом

Другой вопрос, касающийся системы аксиом, – это желательная их независимость. Система аксиом называется независимой, если ни одна из них не является логическим следствием остальных. К примеру, независимость аксиомы о параллельных прямых в рамках аксиоматики евклидовой геометрии удалось установить только в XIX веке, после двух тысячелетий попыток вывести ее как следствие других аксиом системы. Независимость системы аксиом

Доказательство независимости данной аксиомы в системе достигается указанием модели, в которой выполняются все аксиомы, кроме данной, которая заменяется ее отрицанием. Далее желательно, чтобы система аксиом была полной, то есть такой, что добавление к ней новой аксиомы делает новую систему аксиом зависимой. Система аксиом геометрии является полной, но это скорее исключение, чем правило: обычно системы аксиом оказываются неполными. Полнота системы аксиом

Наряду с системой аксиом Гильберта можно назвать и другие варианты аксиоматики евклидовой геометрии: аксиоматика, предложенная в 1904 году Фридрихом Шуром и основанная на понятии движения (наложения) (эта идея используется в учебнике геометрии для средних школ в России, изданного под научным руководством академика А. Н. Тихонова), аксиоматика, основанная на понятии о численном расстоянии, предложенная тогда же Вениамином Федоровичем Каганом, векторная аксиоматика Германа Вейля и др. Другие варианты аксиоматики евклидовой геометрии

При аксиоматическом построении одной и той же теории можно использовать разные системы аксиом. Но они должны быть равносильными. Кроме того, при выборе той или иной системы аксиом математики учитывают, насколько просто и наглядно могут быть получены доказательства теорем в дальнейшем. Но если выбор аксиом условен, то сама наука или отдельная теория не зависят от каких-либо условий, - они являются отражением реального мира. Анализ различных систем

Во второй половине XIX века натуральные числа оказались фундаментом всей математической науки, от состояния которого зависела и прочность всего здания математики. В связи с этим появилась необходимость в строгом логическом обосновании понятия натурального числа, в систематизации того, что с ним связано. Так как математика XIX века перешла к аксиоматическому построению своих теорий, то была разработана аксиоматическая теория натурального числа. Большое влияние па исследование природы натурального числа оказала и созданная в XIX веке теория множеств. Конечно, в созданных теориях понятия натурального числа и действий над ними получили большую абстрактность, но этим всегда сопровождается процесс обобщения и систематизации отдельных фактов. Арифметика

АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ СИСТЕМЫ НАТУРАЛЬНЫХ ЧИСЕЛ Как уже было сказано, натуральные числа получаются при счете предметов и при измерении величин. Но если при измерении появляются числа, отличные от натуральных, то счет приводит только к числам натуральным. Чтобы вести счет, нужна последовательность числительных, которая начинается с единицы и которая позволяет осуществлять переход от одного числительного к другому и столько раз, сколько это необходимо. Иначе говоря, нужен отрезок натурального ряда. Поэтому, решая задачу обоснования системы натуральных чисел, в первую очередь надо было ответить на вопрос о том, что же представляет собой число как элемент натурального ряда. Ответ на него был дан в работах двух математиков - немца Грассмана и итальянца Пеано. Они предложили аксиоматику, в которой натуральное число обосновывалось как элемент неограниченно продолжающейся последовательности. Натуральные числа

Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей, и обозначать символом 1. Аксиома 2. Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а. Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а. Аксиомы из аксиоматической теории натуральных чисел

Слайды и текст этой презентации

Крылова Алина
918 группа

Аксиоматический метод - метод построения теорий, в соответствии с которым разрешается пользоваться в доказательствах лишь аксиомами и ранее выведенными из них утверждениями. Основания для применения аксиоматического метода могут быть разными, что обычно приводит к различению аксиом не только по их формулировкам, но и по их методологическим (прагматическим) статусам.

МЕТОД АНАЛИЗА ЗАТРАТ-РЕЗУЛЬТАТОВ (АЗР)

Метод анализа затрат-результатов

Если условия выполнены, то тогда техника анализа включает в себя следующие шесть ступеней:
Отчетливо представить себе все возможные связи между затратами и выпуском.
Установить должную систему проверки правильности возможных решений.
Разработать методологию достижения практических решений.
Выбрать оптимальный метод.
Создать оптимальную систему на деле.
Доказать ее применяемость к данной проблеме.

Метод анализа затрат-результатов

"Анализ затрат и результатов" представляет собой процесс сопоставления затрат и выгод от возможного варианта. В тех случаях, когда существует более одного варианта, анализ затрат и результатов должен быть проведен в отношении каждого из них. Вариант, гарантирующий наибольшую выгоду или наименьшие затраты, и будет выбран для реализации.

Метод анализа затрат-результатов

Обычно Затраты и результаты одного или нескольких вариантов приводятся в таблице в произвольной форме. Представляя соответствующую информацию, вы должны убедиться в том, что она доступна для понимания и что конечной целью является сравнение всех вариантов на одинаковой основе, что способствует простому выбору самого лучшего варианта.

Слайд 1

Слайд 2

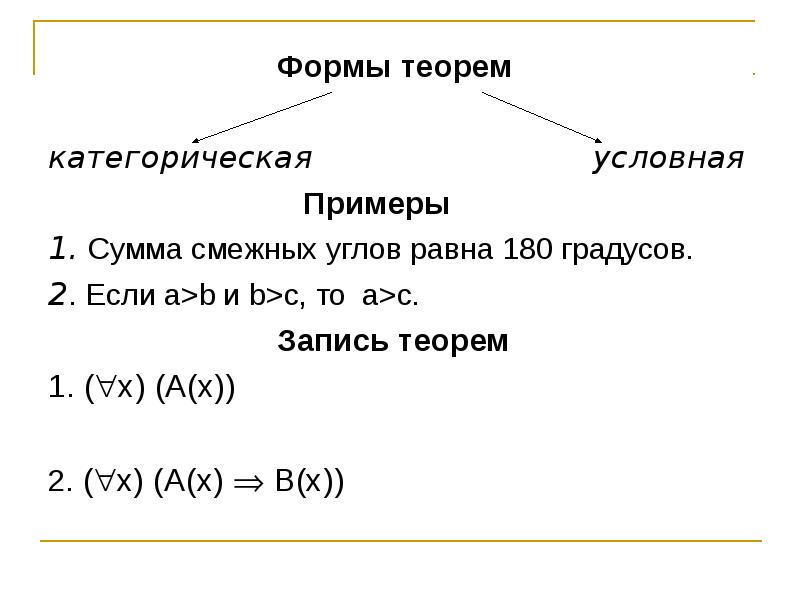
Формы теорем категорическая условная Примеры 1. Сумма смежных углов равна 180 градусов. 2. Если a>b и b>c, то a>c. Запись теорем 1. (x) (A(x)) 2. (x) (A(x)  B(x))

Слайд 3

Части теоремы 1) разъяснительная часть, 2) условие, 3) заключение. (x) (A(x)  B(x))  x - разъяснительная часть теоремы; A(x) - условие теоремы; B(x) - заключение теоремы.

Слайд 4

Этапы методики обучения доказательству теорем 1. Введение теоремы. 2. Разбор теоремы. 3. Получение плана доказательства. 4. Исполнение плана доказательства. 5. Исследование.

Слайд 5

Слайд 6

2. Разбор теоремы Математическая запись теоремы: (1, 2) (1, 2 – вертикальные углы  1=2). Актуализация знаний по разбору теоремы: 1) разъяснительная часть, 2) условие теоремы, 3) заключение теоремы.

Слайд 7

Слайд 8

Пример Все прямоугольники (M) есть параллелограммы (P). Квадрат (S) есть прямоугольник (M). Следовательно, квадрат (S) есть параллелограмм (P).

Слайд 9

Структура силлогизма Все М суть Р - большая посылка(БП) S суть М - меньшая посылка(МП) __________ S суть Р - вывод(В)

Слайд 11

Слайд 12

Доказательством теоремы является цепочка последовательно связанных силлогизмов, устанавливающая истинность теоремы.

Слайд 13

Доказательства теорем 1) прямые (синтетический метод, аналитический метод, метод математической индукции), 2) косвенные ( метод от противного).

Слайд 14

5. Исследование На этапе исследования предлагается доказательство теоремы другим способом (использование при доказательстве других объектов, свойств) или другим методом.

Слайд 15

Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике.

Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них.

Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными.

Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недосказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения.

Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии.

Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах.

После формулировки и доказательства первых геометрических утверждений становится возможным доказывать одни утверждения (теоремы) с помощью других. Доказательства многих теорем приписываются Пифагору и Демокриту.

Гиппократу Хиосскому приписывается составление первого систематического курса геометрии, основанного на определениях и аксиомах. Этот курс и его последующие обработки назывались "Элементы".

Потом, в III в. до н.э., в Александрии появилась книга Евклида с тем же названием, в русском переводе "Начала". От латинского названия "Начал" произошёл термин "элементарная геометрия". Несмотря на то, что сочинения предшественников Евклида до нас не дошли, мы можем составить некоторое мнение об этих сочинениях по "Началам" Евклида. В "Началах" имеются разделы, логически весьма мало связанные с другими разделами. Появление их объясняется только тем, что они внесены по традиции и копируют "Начала" предшественников Евклида.

"Начала" Евклида состоят из 13 книг. 1 - 6 книги посвящены планиметрии, 7 - 10 книги об арифметике и несоизмеримых величинах, которые можно построить с помощью циркуля и линейки. Книги с 11 по 13 были посвящены стереометрии.

"Начала" начинаются с изложения 23 определений и 10 аксиом. Первые пять аксиом - "общие понятия", остальные называются "постулатами". Первые два постулата определяют действия с помощью идеальной линейки, третий - с помощью идеального циркуля. Четвёртый, "все прямые углы равны между собой", является излишним, так как его можно вывести из остальных аксиом. Последний, пятый постулат гласил: "Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то, при неограниченном продолжении этих двух прямых, они пересекутся с той стороны, где углы меньше двух прямых".

Пять "общих понятий" Евклида являются принципами измерения длин, углов, площадей, объёмов: "равные одному и тому же равны между собой", "если к равным прибавить равные, суммы равны между собой", "если от равных отнять равные, остатки равны между собой", "совмещающиеся друг с другом равны между собой", "целое больше части".

Далее началась критика геометрии Евклида. Критиковали Евклида по трём причинам: за то, что он рассматривал только такие геометрические величины, которые можно построить с помощью циркуля и линейки; за то, что он разрывал геометрию и арифметику и доказывал для целых чисел то, что уже доказал для геометрических величин, и, наконец, за аксиомы Евклида. Наиболее сильно критиковали пятый постулат, самый сложный постулат Евклида. Многие считали его лишним, и что его можно и нужно вывести из других аксиом. Другие считали, что его следует заменить более простым и наглядным, равносильным ему: "Через точку вне прямой можно провести в их плоскости не более одной прямой, не пересекающей данную прямую".

Критика разрыва между геометрией и арифметикой привела к расширению понятия числа до действительного числа. Споры о пятом постулате привели к тому, что в начале XIX века Н. И. Лобачевский, Я. Бойяи и К. Ф. Гаусс построили новую геометрию, в которой выполнялись все аксиомы геометрии Евклида, за исключением пятого постулата. Он был заменён противоположным утверждением: "В плоскости через точку вне прямой можно провести более одной прямой, не пересекающей данную". Эта геометрия была столь же непротиворечивой, как и геометрия Евклида.

Модель планиметрии Лобачевского на евклидовой плоскости была построена французским математиком Анри Пуанкаре в 1882г.

На евклидовой плоскости проведём горизонтальную прямую (см. рисунок 1). Эта прямая называется абсолютом (x). Точки евклидовой плоскости, лежащие выше абсолюта, являются точками плоскости Лобачевского. Плоскостью Лобачевского называется открытая полуплоскость, лежащая выше абсолюта. Неевклидовы отрезки в модели Пуанкаре - это дуги окружностей с центром на абсолюте или отрезки прямых, перпендикулярных абсолюту (AB, CD) . Фигура на плоскости Лобачевского - фигура открытой полуплоскости, лежащей выше абсолюта (F) . Неевклидово движение является композицией конечного числа инверсий с центром на абсолюте и осевых симметрий, оси которых перпендикулярны абсолюту. Два неевклидовых отрезка равны, если один из них неевклидовым движением можно перевести в другой. Таковы основные понятия аксиоматики планиметрии Лобачевского.

Все аксиомы планиметрии Лобачевского непротиворечивы. Определение прямой следующее: "Неевклидова прямая - это полуокружность с концами на абсолюте или луч с началом на абсолюте и перпендикулярный абсолюту". Таким образом, утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой a и точки A, не лежащей на этой прямой, но и для любой прямой a и любой не лежащей на ней точки A (см. рисунок 2) .

За геометрией Лобачевского возникли и другие непротиворечивые геометрии: от евклидовой отделилась проективная геометрия, сложилась многомерная евклидова геометрия, возникла риманова геометрия (общая теория пространств с произвольным законом измерения длин) и др. Из науки о фигурах в одном трёхмерном евклидовом пространстве геометрия за 40 - 50 лет превратилась в совокупность разнообразных теорий, лишь в чём-то сходных со своей прародительницей - геометрией Евклида.

Читайте также: