Всегда ли квадрат иррационального числа является рациональным числом кратко

Обновлено: 04.07.2024

Оказывается, что для нужд самой математики как, впрочем, и для практики, уже введённых рациональных чисел не хватает. Исторически числа, отличные по своей природе от рациональных, впервые появились уже при желании вычислить диагональ квадрата по его стороне.

Покажем, что длина такой диагонали не может быть выражена рациональным числом. Рассмотрим квадрат со стороной, равной 1. Пусть длина его диагонали равна . Тогда, по теореме Пифагора, имеем: то есть Предположим, что – рациональное число. Тогда существуют такие числа что и дробь несократима. Получаем: Из этого равенства следует, что, так как правая его часть делится на 2, то и его левая часть делится на 2. Значит и число делится на 2. Другими словами существует такое целое число что . Но тогда Однако из последнего равенства аналогично следует, что число делится на 2. Последнее обстоятельство приводит к противоречию, так как числа и не могут быть одновременно чётными (по предположению, дробь несократима). Значит, не существует такого рационального числа, которое бы выражало длину диагонали квадрата.

Числа, которые не являются рациональными, то есть не являются ни целыми, ни представимыми в виде дроби вида , где – целое число, а – натуральное, называются иррациональными .

Из нашего примера следует, что такие числа существуют: длина диагонали квадрата со стороной 1 является именно таким числом. Аналогично можно доказать, что не существует рационального числа, квадрат которого равен 5, 7, 10, то есть числа являются иррациональными. Теперь вспомним, что любое рациональное число может быть представлено в виде периодической десятичной дроби и наоборот, любая десятичная периодическая дробь может быть представлена в виде рационального числа.

Любое иррациональное число можно записать в виде бесконечной непериодической дроби, и любая непериодическая дробь является иррациональным числом.

Множества рациональных и иррациональных чисел вместе составляют множество действительных чисел .

Каждому действительному числу отвечает точка на координатной прямой, и наоборот, каждая точка на координатной прямой соответствует действительному числу. Действительно, для любой точки координатной прямой достаточно найти расстояние до неё от начала координат, а потом поставить перед этим числом знак плюс (+), если точка располагается правее начала координат, и знак минус (–) – если левее.

Изученные множества чисел обозначаются следующим образом:

– множество натуральных чисел;
– множество неотрицательных целых чисел (расширенный ряд натуральных чисел);
– множество целых чисел;
– множество рациональных чисел;
– множество иррациональных чисел;
– множество действительных чисел.

Множество целых чисел содержится во множестве рациональных чисел которое, в свою очередь, является частью всего множества действительных чисел Эти отношения можно записать кратко в виде ,

Совершенно аналогично десятичным дробям вводятся правила действия над действительными числами.

Сложение. Сумма двух действительных чисел одного знака есть число того же знака. Модуль такой суммы равен сумме модулей слагаемых.

Сумма двух действительных чисел разных знаков имеет тот же знак, что и большее по модулю слагаемое. Модуль суммы равен разности модулей большего и меньшего слагаемых.

Вычитание. Чтобы вычесть из одного действительного числа другое действительное число, нужно к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение и деление. Произведение (частное) двух действительных чисел одного знака есть число положительное. Произведение (частное) двух действительных чисел разных знаков есть число отрицательное. Модуль произведения (частного) двух действительных чисел равен произведению (частному) модулей этих чисел.

Арифметические операции над действительными числами обладают следующими свойствами ( основные законы алгебры ).

( переместительный закон сложения ).
( сочетательный закон сложения ).
( свойство нуля ).
( свойство противоположного числа ).
( переместительный закон умножения ).
( сочетательный закон ).
( распределительный закон умножения относительно сложения ).
( основное свойство единицы ).
( существование обратного числа ).

Сравнение действительных чисел производится совершенно аналогично сравнению рациональных чисел. А именно, говорят, что действительное число больше другого действительного числа , и обозначают этот факт так: , если разность – положительное действительное число. Говорят, что действительное число меньше другого действительного числа , и обозначают этот факт так: , если разность – отрицательное действительное число. На действительные числа совершенно аналогично переносятся понятия отношений ≤ и ≥. При этом числовые неравенства обладают следующими свойствами:

Понятие иррациональности можно встретить в философских учениях, логических концепциях и даже в психологической типологии Карла Юнга. Но нас все-таки интересует математика: что значит иррациональное число и зачем оно нужно.

О чем эта статья:

6 класс, 8 класс

Определение иррациональных чисел

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:

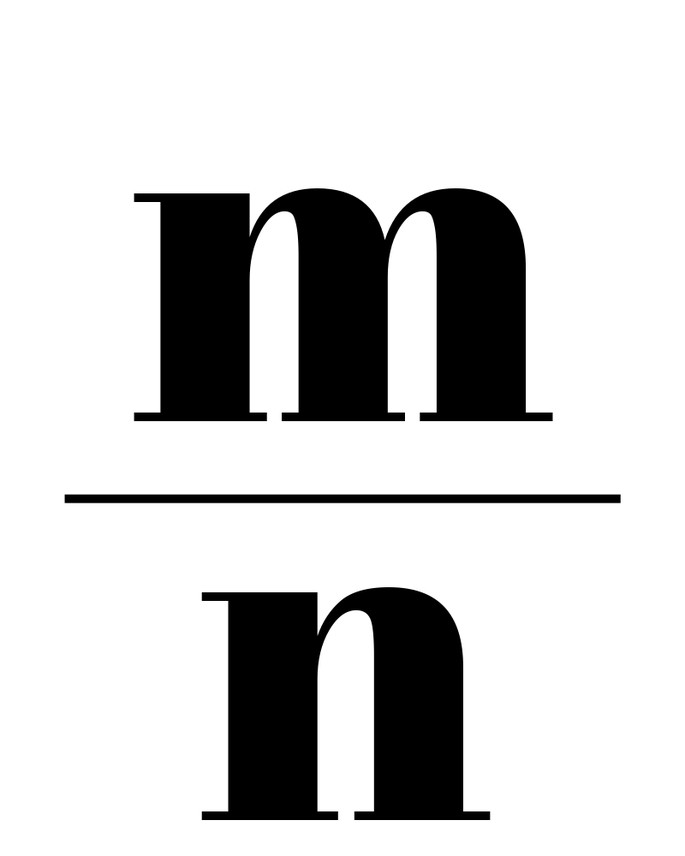
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры иррациональных чисел:

π = 3,1415926.
√2 = 1,41421356.
e = 2,71828182…
√8 = 2.828427.
-√11= -3.31662…

Множество иррациональных чисел договорились обозначать латинской буквой I.

Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Если натуральное число n не является точным квадратом, т. е. n ≠ k 2 , где k ∈ Q, то √n — иррациональное число.

Свойства иррациональных чисел

Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.

Свойства иррациональных чисел:

результат суммы иррационального числа и рационального равен иррациональному числу;
результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Определение рациональных чисел

А теперь наоборот: рассмотрим противоположное заданной теме определение.

Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.

Рациональные числа — это те, которые можно представить в виде:

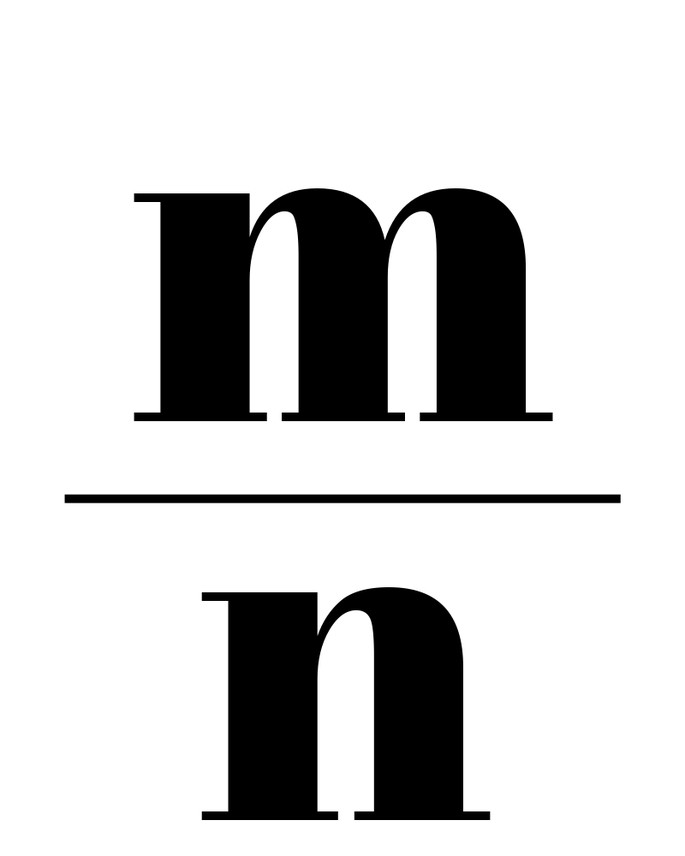
где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

десятичная дробь 1,15 — это 115/100;
десятичная дробь 0,2 — это 1/5;
целое число 0 — это 0/1;
целое число 6 — это 6/1;
целое число 1 — это 1/1;
бесконечная периодическая дробь 0,33333. — это 1/3;
смешанное число это 25/10;
отрицательная десятичная дробь -3,16 — это -316/100.

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Данная статья посвящена изучению темы "Рациональные числа". Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа - числа, которые можно представить в виде положительной обыкновенной дроби a b , отрицательной обыкновенной дроби - a b или числа ноль.

Таким образом, можно оставить ряд свойств рациональных чисел:

Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1 n .
Любое целое число, включая число 0 , является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15 = 15 1 , - 352 = - 352 1 .
Любая положительная или отрицательная обыкновенная дробь a b является рациональным числом. Это следует напрямую из данного выше определения.
Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом.
Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа 5 , 105 , 358 , 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа - 2 , - 358 , - 936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 3 5 , 8 7 , - 35 8 также являются примерами рациональных чисел.

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа - это такие числа, которые можно представить в виде дроби ± z n , где z - целое число, n - натуральное число.

Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:

0 n = 0 ÷ n = 0 ; - m n = ( - m ) ÷ n = - m n .

Таким образом, можно записать:

z n = z n , п р и z > 0 0 , п р и z = 0 - z n , п р и z 0

Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа - 3 , 0 , 5 , - 7 55 , 0 , 0125 и - 1 3 5 . Все эти числа являются рациональными, так как их можно записать в виде дроби с целым числителем и натуральным знаменателем: - 3 1 , 0 1 , - 7 55 , 125 10000 , 8 5 .

Приведем еще одну эквивалентную форму определения рациональных чисел.

Определение 3. Рациональные числа

Рациональное число - это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.

Данное определение напрямую следует из самого первого определения этого пункта.

Подведем итог и сформулируем резюме по данному пункту:

Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.
Каждое рациональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель - натуральным числом.
Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.

Какое из чисел является рациональным?

Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.

Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос "рационально ли число?" является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.

Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения - рациональное число.

Например, значение выражения 2 · 3 1 8 - 0 , 25 0 , ( 3 ) является рациональным числом и равно 18 .

Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.

Теперь разберемся со знаком корня.

Оказывается, что число m n , заданное в видя корня степени n от числа m рационально лишь тогда, когда m является n -ой степенью какого-то натурального числа.

Обратимся к примеру. Число 2 не является рациональным. Тогда как 9 , 81 - рациональные числа. 9 и 81 - полные квадраты чисел 3 и 9 соответственно. Числа 199 , 28 , 15 1 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел.

Теперь возьмем более сложный случай. Является ли рациональным число 243 5 ? Если возвести 3 в пятую степень, получается 243 , поэтому исходное выражение можно переписать так: 243 5 = 3 5 5 = 3 . Следовательно, данное число рационально. Теперь возьмем число 121 5 . Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст 121 .

Для того, чтобы узнать, является ли логарифм какого-то числа a по основанию b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число log 2 5 . Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби log 2 5 = m n .По свойствам логарифма и свойствам степени справедливы следующие равенства:

5 = 2 log 2 5 = 2 m n 5 n = 2 m

Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log 2 5 не является рациональным числом.

Стоит отметить, что при определении рациональности и иррациональности чисел не стоит принимать скоропостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом. Наглядный пример: 2 · 2 = 2 .

Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида 2 log 2 3 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: 2 log 2 3 = 3 .

10 Смотреть ответы Добавь ответ +10 баллов

Ответы 10

я думаю что нет не всегда

прости если не правильно ответила.

15 в квадрате = 225, можно легко с поиощью калькулятора проверить)))

225 в квадрате-это 15
Рада была

Другие вопросы по Математике

В17 ч 45 мин из дома одновременно вышли коля и серёжа и пошли в одном направлении.в какое время расстояние между ними стало равным 300 м,если коля двигался со скоростью 80 м/мин,а.

Вогороде две овощные базы.по ошибке на одну из них завезли в 4 раза больше картофеля,чем на другую.чтобы уровнять количество картофеля на обеих базах,пришлось с первой базы перевез.

Читайте также: