В чем заключается принцип независимости действия сил кратко
Обновлено: 02.07.2024
Допущение о малости деформаций делает возможным применение принципа независимости действия сил. Этот принцип в сопротивлении материалов формулируется следующим образом: результат одновременного действия нескольких групп сил совпадает с суммой результатов, вызванных каждой группой сил в отдельности.
Для доказательства данного принципа рассмотрим двухопорную балку, изображенную на рис. 1.14. Приложим в некоторой произвольной точке силу Р1, которая вызовет в точке А перемещение , которое равно , где - коэффициент пропорциональности. Теперь устраним действие силы Р1 и в некоторой другой произвольной точке приложим силу Р2, от действия которой точка переместится на величину .
Очевидно, что коэффициенты пропорциональности и не равны между собой, так как силы Р1 и Р2 приложены в разных точках балки.
| P2 |
| fA2 |
| fA1 |
| P1 |
| A |
| P2 |
| A |
| fA1+fA2 |
| P1 |
| A |
Рис. 1.14. Принцип независимости действия сил
Рассмотрим теперь совместное действие сил Р1 и Р2. Приложим сначала силу Р1, а затем, не снимая ее, силу Р2. Тогда суммарное перемещение точки А можно определить по формуле . Коэффициент будет иметь тоже значение, т.к. сила Р1 была приложена к ненагруженной балке, коэффициент же пропорциональности для силы Р2 обозначен как , т.к. сила Р2 приложена к системе, на которую уже действует сила Р1. Если коэффициенты и различны, то следует признать, что коэффициент зависит от силы Р1 (даже имеющей нулевое значение), но это противоречит принятому предположению, о линейной зависимости перемещений от действующей силы. Следовательно, и тогда . Видно, что суммарное перемещение в точке А определяется как сумма перемещений от независимых действий сил Р1 и Р2.
Таким образом, принцип независимости действия сил (принцип суперпозиции) сформулируем так: результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
При малых деформациях большинство тел можно считать линейно-упругими. Это означает, что при снятии внешней нагрузки тело полностью восстанавливает свою форму и размеры (идеальная упругость), и, кроме того, наблюдается линейная связь между силами P и смещениями D:
где k – коэффициент пропорциональности (жесткости), зависящий от вида и материала конструкции.
Действующие на упругое тело внешние силы совершают над ним работу. Эта работа, согласно закону сохранения механической энергии, переходит в потенциальную энергию упругой деформации. При сделанных выше допущениях и в предположении о квазистатическом приложении силы P потенциальная энергия легко определяется с помощью теоремы Клапейрона.
При медленном (квазистатическом) нагружении вся работа внешней нагрузки переходит в потенциальную энергию U:

.
Рассмотрим пример работы под нагрузкой консольного стержня (рис. 1.15а) или двухопорной балки (рис. 1.15б), на которые действует сила P. При этом характерные точки обеих систем переместятся на величину D, а при дополнительном нагружении - на .
Рис. 1.15. К определению работы внешних сил

Элементарная работа равна (рис. 1.15в) .

Полная работа, совершаемая силой Р, вызвавшей перемещение , будет

.
Этот интеграл представляет собой заштрихованную площадь диаграммы, и, значит, для линейно-упругой системы будет численно равен площади треугольника:

.
Данное равенство называется теоремой Клапейрона и имеет очень большое значение при исследовании перемещений различных упругих систем.
При действии на систему нескольких сил (n) теорема Клапейрона принимает вид:

.
Средневековье: основные этапы и закономерности развития: Эпоху Античности в Европе сменяет Средневековье. С чем связано.
Основные этапы развития астрономии. Гипотеза Лапласа: С точки зрения гипотезы Лапласа, это совершенно непонятно.
Пример оформления методической разработки: Методическая разработка - разновидность учебно-методического издания в помощь.
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.
Ускорение, приобретаемое точкой под действием нескольких сил___________________________________________
- результирующая сила. Сила может быть разложена на две составляющие — тангенциальную ( ) и нормальную (см. рисунок).
Тангенциальная и нормальная составляющие силы_________________________________________________________
Разложение силы на составляющие приводит к существенному упрощению решения задач. Например, на рисунке действующая сила F = та разложена на два компонента: тангенциальную силу FT (направлена по касательной к траектории) и нормальную силу Fn (направлена по нормали к центру кривизны).
♦ Если на материальную точку действует одновременно несколько
сил, то, согласно принципу независимости действия сил, под F
во втором законе Ньютона понимают результирующую силу.
1.22 Третий закон Ньютона_______
Формулировка третьего закона Ньютона____________
Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
[F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой]
Силы в третьем законе Ньютона________________________________________________________________
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
♦ Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Формулировка принципа независимости действия сил______________________________________________________
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, согласно второму закону Ньютона, как будто других сил нет.
Ускорение, приобретаемое точкой под действием нескольких сил___________________________________________
- результирующая сила. Сила может быть разложена на две составляющие — тангенциальную ( ) и нормальную (см. рисунок).
Тангенциальная и нормальная составляющие силы_________________________________________________________
Разложение силы на составляющие приводит к существенному упрощению решения задач. Например, на рисунке действующая сила F = та разложена на два компонента: тангенциальную силу FT (направлена по касательной к траектории) и нормальную силу Fn (направлена по нормали к центру кривизны).
♦ Если на материальную точку действует одновременно несколько
сил, то, согласно принципу независимости действия сил, под F
во втором законе Ньютона понимают результирующую силу.
1.22 Третий закон Ньютона_______
Формулировка третьего закона Ньютона____________
Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
[F12 — сила, действующая на первую материальную точку со стороны второй; F21 — сила, действующая на вторую материальную точку со стороны первой]
Силы в третьем законе Ньютона________________________________________________________________
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
♦ Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Принцип независимости действия сил : если на материальную точку одновременно действует несколько сил, то каждая из них сообщает точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было. [1]
Принцип независимости действия сил ( широко используемый в сопротивлении материалов и других науках) позволяет расчленить сложную задачу на ряд простых, однако его можно использовать лишь при выполнении третьего и четвертого ддпушедий. [2]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, величина которого не зависит ни от состояния движения тела, ни от действия на тело других сил. [3]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от каждой силы в отдельности. [4]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, величина которого не зависит ни от состояния движения тела, ни от действия на тело других сил. [5]
Принцип независимости действия сил заключается в том, что каждая действующая на данное тело сила сообщает ему ускорение, которое не зависит ни от состояния движения тела, ни от действия на тело других сил. [6]
Принцип независимости действия сил справедлив для материалов в том диапазоне, в котором они следуют закону Гука; он неприменим для многих случаев конструкционного использования термопластов, которые даже при нормальных температурах и относительно невысоких уровнях напряжений проявляют вязкоупру-гие свойства, например ползучесть. [7]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности. [8]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которыг эта точка получила бы от каждой силы в отдельности. [9]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которую эта точка получила бы от каждой силы в отдельности. [10]
Принцип независимости действия сил и принцип сложения не применимы, когда одна из сил качественно меняет способ действия другой силы, например, в случае продольно-поперечного изгиба. [11]
Принцип независимости действия сил является основным руководящим принципом при решении подавляющего большинства задач сопротивления материалов. [12]
Принцип независимости действия сил позволяет расчленять нагрузку на отдельные части и вести расчет порознь на действие каждой из них. Простейшей базовой нагрузкой является единичная сосредоточенная сила, приложенная в определенной точке и в определенном направлении. [13]
Принцип независимости действия сил опирается на известный в физике закон Гука, характеризующий линейную зависимость между нагрузкой и деформацией. В случаях, когда процесс деформирования тела не следует закону Гука, а также в некоторых особых случаях принцип независимости действия сил применять нельзя. [14]
Принцип независимости действия сил формулируется так: при одновременном действии на материальную точку нескольких сил ее ускорение равно векторной сумме ускорений, которые эта точка получила бы от действия каждой силы в отдельности.
Пусть к материальной точке А приложены силы F1и F2, равнодействующая которых равна F. На основании аксиомы параллелограмма запишем
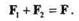
Разделим обе части равенства на массу точки, получим


Применяя последовательно аксиому параллелограмма, можно сказать, что при одновременном действии на материальную точку нескольких сил ее ускорение будет таким, как если бы действовала одна равнодействующая сила
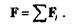
Пользуясь принципом независимости действия сил, выведем уравнение движения материальной точки в дифференциальной форме.
Пусть материальная точка А массой т движется в плоскости чертежа под действием силы F = Fi с ускорением а, тогда

Спроецируем это векторное равенство на две взаимно перпендикулярные оси координат х и у (оси и вектор силы F лежат в одной плоскости) и получим уравнения плоского движения материальной точки в координатной форме:

Применяя теорему о проекции ускорения на координатную ось, можно эти уравнения записать в виде дифференциальных уравнений плоского движения материальной точки:

В этих уравнениях X, Y — алгебраические суммы проекций сил,
действующих на точку, на соответствующие координатные оси; х и у — текущие координаты точки.
С помощью выведенных в этом параграфе уравнений решаются две основные задачи динамики: 1) по заданному движению точки определить действующие на нее силы; 2) зная действующие на точку силы, определить ее движение.
В тех случаях, когда при решении задач имеем дело с несвободной материальной точкой, необходимо применять принцип освобождаемости, т. е. отбросить связи и заменить их реакциями, учитывая последние в уравнениях движения наравне с действующими на точку активными силами.
Пример 13.1.Движение тела массой 0,5 кг выражается уравнениями

где х и у — в сантиметрах, t—в секундах. Определить силу, действующую на тело.
Решение. Данный пример относится к первой задаче динамики. Прежде всего, пользуясь теоремой о проекции ускорения на координатную ось, определим проекции ускорения на оси х и у:

Подставив эти значения в уравнения движения материальной точки, получим:

По проекциям силы, действующей на тело, видно, что она параллельна оси ординат, направлена в сторону отрицательных ординат и по модулю равна


Пример 13.2. Кривошип ОА длиной l, вращаясь равномерно с угловой скоростью , перемещает кулису, движущуюся поступательно вдоль направляющих I—I (рис. 13.1). Найти, пренебрегая трением, чему при этом равна сила давления F камня А на кулису, если сила тяжести ее равна G.
Решение. Данный пример относится к первой задаче динамики.
Применим принцип освобождаемости, отбросим связи кулисы и заменим их реакциями. Реакция N перпендикулярна направляющим кулисы, а сила давления F перпендикулярна кулисе, так как по условию трением пренебрегаем.
Кулиса движется возвратно-поступательно, следовательно, все ее точки движутся одинаково. Составим уравнение движения проекции точки А на ось х, которое и будет кинематическим уравнением движения кулисы:

Применив теорему о проекции ускорения на координатную ось, определим ускорение кулисы

Составим уравнение движения кулисы в координатной форме:

Спроецировав действующие накулису силы на осьд: и подставивзначения массы и ускорения, получим


Следовательно, сила давления ползуна на кулису изменяется пропорционально расстоянию кулисы от оси кривошипа.
Пример 13.3.На материальную точку массой 4 кг лежащую на гладкой горизонтальной плоскости действует горизонтальная сила F = 12 Н. С какой скоростью будет двигаться материальная точка через t = 10 с, если до приложения силы эта точка находилась в покое?
Решение. Данный пример относится ко второй задаче динамики.
Так как данная материальная точка лежит на гладкой горизонтальной плоскости, то под действием горизонтальной постоянной силы F точка будет двигаться прямолинейно равноускоренно. Направив ось дс вдоль траектории точки, запишем уравнение движения:

Спроецировав на ось х действующие на точку силы и подставив в это уравнение значение массы, определим ускорение

Применим формулу скорости равноускоренного движения

Подставив значения, получим
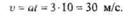
Пример 13.4. В результате полученного толчка кирпич начал скользить с начальной скоростью 0 =2 м/с по неподвижной ленте конвейера, расположенного под углом = /6 рад к горизонту. Определить перемещение s кирпича за про-

межуток времени t = 2с, если коэффициент трения скольжения кирпича о ленту конвейера f = 0,4; кирпич считать точечной массой (рис 13.2).
Решение. Данный пример относится ко второй задаче динамики. Выберем систему координат хОу таким образом, чтобы начало координат было в начальном положении тела, ось х была направлена вдоль ленты конвейера вниз, а ось у — перпендикулярно ленте конвейера вверх. Применив принцип освобождаемое, рассмотрим кирпич как материальную точку, движущуюся вдоль оси х под действием силы тяжести G, нормальной реакции N и силы трения Fтр.
Составим уравнения движения материальной точки:
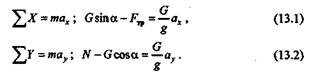
Кроме того, на основании второго закона трения скольжения можно записать

Так как материальная точка движется вдоль оси х, то ау = 0, в результате чего из уравнения (13.2) имеем

Подставив это выражение в уравнение (13.3), получим

Полученное выражение подставим в уравнение (13.1):

Сокращая это равенство на G и учитывая, что ах =а ,определим ускорение кирпича:

или, вынеся gcosa за скобку, получим

Так как правая часть этого равенства содержит только постоянные величины, то ускорение кирпича—величина постоянная, причем возможны три случая движения:
1) если tg > f, то а > 0 и движение будет равноускоренным;
2) если tg = f, тo a = 0 и движение будет равномерным;
3) если tg f, т. е. а > 0, следовательно, движение кирпича было равноускоренным.
Движение материальной точки,
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.008)
Читайте также:
- Какие политические силы были основными при организации переворотов кратко
- Анализ стихотворения пушкина няне 5 класс по плану кратко
- Можно ли считать что эти статьи капитуляции закрепляли навечно за францией льготы кратко
- Что такое склонение в астрономии кратко
- Правильно ли утверждать что подписав международный договор государство лишается суверенитета кратко

