В чем заключается геометрический смысл определенного интеграла кратко

Обновлено: 05.07.2024

Вычисление площади является основным в теории площадей. Возникает вопрос о ее нахождении, когда фигура имеет неправильную форму или необходимо прибегнуть к ее вычислению через интеграл.

Данная статья рассказывает о вычислении площади криволинейной трапеции по геометрическому смыслу. Это позволяет выявлять связь между интегралом и площадью криволинейной трапеции. Если дана функция f ( x ) , причем непрерывная на интервале [ a ; b ] , знак перед выражением не меняется.

Криволинейная трапеция

Фигура, обозначенная как G , ограничена линиями вида y = f ( x ) , y = 0 , x = a и x = b , называется криволинейной трапецией. Она принимает обозначение S ( G ) .

Рассмотрим на рисунке, приведенном ниже.

Для вычисления криволинейно трапеции необходимо разбить отрезок [ a ; b ] на количество n частей x i - 1 ; x i , i = 1 , 2 , . . . , n с точками, определенными на a = x 0 x 1 x 2 . . . x n - 1 x n = b , причем дать обозначение λ = m a x i = 1 , 2 , . . . , n x i - x i - 1 с точками x i , i = 1 , 2 , . . . , n - 1 . Необходимо выбрать так, чтобы λ → 0 при n → + ∞ , тогда фигуры, которые соответствуют нижней и верхней частям Дарбу, считаются входящей Р и объемлющей Q многоугольными фигурами для G . Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что P ⊂ G ⊂ Q , причем при увеличении количества точек разбиения n , получим неравенство вида S - s ε , где ε является малым положительным числом, s и S являются верхними и нижними суммами Дабру из отрезка [ a ; b ] . Иначе это запишется как lim λ → 0 S - s = 0 . Значит, при обращении к понятию определенного интеграла Дарбу, получим, что lim λ → 0 S = lim λ → 0 s = S G = ∫ a b f ( x ) d x .

Из последнего равенства получим, что определенный интеграл вида ∫ a b f ( x ) d x является площадью криволинейной трапеции для заданной непрерывной функции вида y = f ( x ) . Это и есть геометрический смысл определенного интеграла.

При вычислении ∫ a b f ( x ) d x получим площадь искомой фигуры, которая ограничивается линиями y = f ( x ) , y = 0 , x = a и x = b .

Замечание: Когда функция y = f ( x ) является неположительной из отрезка [ a ; b ] , тогда получаем, что площадь криволинейной трапеции вычисляется, исходя из формулы S ( G ) = - ∫ a b f ( x ) d x .

Вычислить площадь фигуры, которая ограничена заданными линиями вида y = 2 · e x 3 , y = 0 , x = - 2 , x = 3 .

Для того, чтобы решить, необходимо для начал построить фигуру на плоскости, где имеется прямая y = 0 , совпадающая с О х , с прямыми вида x = - 2 и x = 3 , параллельными оси о у , где кривая y = 2 · e x 3 строится при помощи геометрических преобразований графика функции y = e x . Построим график.

Отсюда видно, что необходимо найти площадь криволинейной трапеции. Вспоминая геометрический смысл интеграла, получаем, что искомая площадь и будет выражена определенным интегралом, который необходимо разрешить. Значит, необходимо применить формулу S ( G ) = ∫ - 2 3 2 · e x 3 d x . Такой неопределенный интеграл вычисляется, исходя из формулы Ньютона-Лейбница

S ( G ) = ∫ - 2 3 2 · e x 3 d x = 6 · e x 3 - 2 3 = 6 · e 3 3 - 6 · e - 2 3 = 6 · e - e - 2 3

Ответ: S ( G ) = 6 · e - e - 2 3

Замечание: Для нахождения площади криволинейной трапеции не всегда можно построить фигуру. Тогда решение выполняется следующим образом. При известной функции f ( x ) неотрицательной или неположительной на отрезке [ a ; b ] , применяется формула вида S G = ∫ a b f ( x ) d x или S G = - ∫ a b f ( x ) d x .

Произвести вычисление площади, ограниченной линиями вида y = 1 3 ( x 2 + 2 x - 8 ) , y = 0 , x = - 2 , x = 4 .

Для построения этой фигуры получим, что у = 0 совпадает с О х , а х = - 2 и х = 4 являются параллельными О у . График функции y = 1 3 ( x 2 + 2 x - 8 ) = 1 3 ( x + 1 ) 2 - 3 - это парабола с координатами точки ( - 1 ; 3 ) , являющейся ее вершиной с направленными вверх ветвями. Чтобы найти точки пересечения параболы с О х , необходимо вычислить:

1 3 ( x 2 + 2 x - 8 ) = 0 ⇔ x 2 + 2 x - 8 = 0 D = 2 2 - 4 · 1 · ( - 8 ) = 36 x 1 = - 2 + 36 2 = 2 , x 2 = - 2 - 36 2 = - 4

Значит, парабола пересекает ох в точках ( 4 ; 0 ) и ( 2 ; 0 ) . Отсюда получим, что фигура, обозначенная как G , получит вид, изображенный на рисунке ниже.

Данная фигура не является криволинейной трапецией, потому как функция вида y = 1 3 ( x 2 + 2 x - 8 ) изменяет знак на промежутке [ - 2 ; 4 ] . Фигура G может быть представлена в виде объединений двух криволинейных трапеций G = G 1 ∪ G 2 , исходя из свойства аддитивности площади, имеем, что S ( G ) = S ( G 1 ) + S ( G 2 ) . Рассмотрим график, приведенный ниже.

Отрезок [ - 2 ; 4 ] считается неотрицательной областью параболы, тогда отсюда получаем, что площадь будет иметь вид S G 2 = ∫ 2 4 1 3 ( x 2 + 2 x - 8 ) d x . Отрезок [ - 2 ; 2 ] неположительный для функции вида y = 1 3 ( x 2 + 2 x - 8 ) , значит, исходя из геометрического смысла определенного интеграла, получим, что S ( G 1 ) = - ∫ - 2 2 1 3 ( x 2 + 2 x - 8 ) d x . Необходимо произвести вычисления по формуле Ньютона-Лейбница. Тогда определенный интеграл примет вид:

S ( G ) = S ( G 1 ) + S ( G 2 ) = - ∫ - 2 2 1 3 ( x 2 + 2 x - 8 ) d x + ∫ 2 4 1 3 ( x 2 + 2 x - 8 ) d x = = - 1 3 x 3 3 + x 2 - 8 x - 2 2 + 1 3 x 3 3 + x 2 - 8 x 2 4 = = - 1 3 2 3 3 + 2 2 - 8 · 2 - - 2 3 3 + ( - 2 ) 2 - 8 · ( - 2 ) + + 1 3 4 3 3 + 4 3 - 8 · 4 - 2 3 3 + 2 2 - 8 · 2 = = - 1 3 8 3 - 12 + 8 3 - 20 + 1 3 64 3 - 16 - 8 3 + 12 = 124 9

Стоит отметить, что нахождение площади не верно по принципу S ( G ) = ∫ - 2 4 1 3 ( x 2 + 2 x - 8 ) d x = 1 3 x 3 3 + x 2 - 8 x - 2 4 = = 1 3 4 3 3 + 4 3 - 8 · 4 - - 2 3 3 + - 2 2 - 8 · - 2 = 1 3 64 3 - 16 + 8 3 - 20 = - 4

Так как полученное число является отрицательным и представляет собой разность S ( G 2 ) - S ( G 1 ) .

Ответ: S ( G ) = S ( G 1 ) + S ( G 2 ) = 124 9

Если фигуры ограничены линиями вида y = c , y = d , x = 0 и x = g ( y ) , а функция равна x = g ( y ) , причем непрерывна и имеет неменяющийся знак на промежутке [ c ; d ] , то их называют криволинейными тарпециями. Рассмотрим на рисунке, приведенном ниже.

Геометрический смысл определенного интеграла

Геометрический смысл определенного интеграла ∫ c d g ( y ) d y заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида x = g ( y ) , расположенной на интервале [ c ; d ] .

Справедливо считать, что S ( G ) = - ∫ c d g ( y ) d y имеет место быть для непрерывной и неположительной функции x = g ( x ) , расположенном на отрезке [ c ; d ] .

Произвести вычисление фигуры, которая ограничена осью ординат и линиями x = 4 ln y y + 3 , y = 1 , y = 4 .

Построение графика x = 4 ln y y + 3 не является простым. Поэтому необходимо решить без чертежа. Вспомним, что функция определена для всех положительных значений y . Рассмотрим значения функции, имеющиеся на отрезке [ 1 ; 4 ] . По свойствам элементарных функций знаем, что логарифмическая функция возрастает на всей области определения. Тогда не отрезке [ 1 ; 4 ] является неотрицательной. Значит имеем, что ln y ≥ 0 . Имеющееся выражение ln y y , определенное на том же отрезке, неотрицательно. Можно сделать вывод, что функция x = 4 ln y y + 3 является положительной на интервале, равном [ 1 ; 4 ] . Получаем, что фигура на этом интервале является положительной. Тогда ее площадь должна вычисляться по формуле S ( G ) = ∫ 1 4 4 ln y y + 3 d y .

Необходимо произвести вычисление неопределенного интеграла. Для этого необходимо найти первообразную функции x = 4 ln y y + 3 и применить формулу Ньютона-Лейбница. Получаем, что

∫ 4 ln y y + 3 d y = 4 ∫ ln y y d y + 3 ∫ d y = 4 ∫ ln y d ( ln y ) + 3 y = = 4 ln 2 y 2 + 3 y + C = 2 ln 2 y + 3 y + C ⇒ S ( G ) = ∫ 1 4 4 ln y y + 3 d y = 2 ln 2 + y + 3 y 1 4 = = 2 ln 2 4 + 3 · 4 - ( 2 ln 2 1 + 3 · 1 ) = 8 ln 2 2 + 9

Рассмотрим чертеж, приведенный ниже.

Ответ: S ( G ) = 8 ln 2 2 + 9

Итоги

В данной статье мы выявили геометрический смысл определенного интеграла и изучили связь с площадью криволинейной трапеции. Отсюда следует, что мы имеем возможность вычислять площадь сложных фигур при помощи вычисления интеграла для криволинейной трапеции. В разделе нахождения площадей и фигур, которые ограниченными линиями y = f ( x ) , x = g ( y ) , данные примеры рассмотрены подробно.

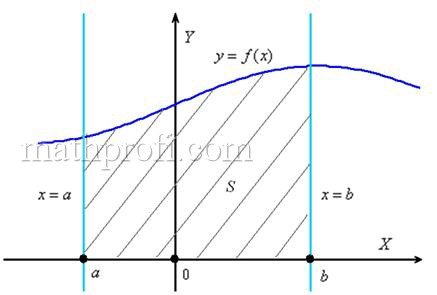
Начнем с криволинейной трапеции. Криволинейной трапецией называется плоская фигура, ограниченная осью , прямыми , и графиком функции , которая непрерывна и неотрицательна на отрезке :

И смысл прост. Определённый интеграл численно равен площади (заштрихована на чертеже) этой криволинейной трапеции. Площадь, как многие помнят, стандартно обозначается буквой .

В самом начале курса я говорил, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии, это число – есть ПЛОЩАДЬ.

Рассмотрим, например, определенный интеграл . Подынтегральная функция задает на плоскости вполне определённую непрерывную кривую, располагающуюся выше оси абсцисс (нам даже не важнА её форма), а сам определенный интеграл численно равен площади соответствующей криволинейной трапеции.

И вообще, любому определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Эта фигура не обязательно расположена выше оси абсцисс, она может располагаться и ниже, может располагаться и там и там; может быть более простой или более сложной.

Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

Определенным интегралом от функции y = f (x) относительно отрезка [a;b] называют предел интегральных сумм Sn при n, стремящемся к бесконечности.

В данном выражении:

a и b являются пределами интегрирования;
f(x) представляет собой подынтегральную функцию, площадь под которой требуется определить.

представляет собой площадь криволинейной трапеции подынтегральной функции f(x) в пределах от a до b.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В чем заключается геометрический смысл определенного интеграла

Геометрический смысл определенного интеграла можно записать таким образом:

К примеру, масса неоднородного стержня AD будет представлена с помощью равенства:

Скорость перемещения точки вдоль прямой составит:

Вычисление определенного интеграла и площади криволинейной трапеции основано на теореме.

Теорема о вычислении определенного интеграла

В том случае, когда f является непрерывной и неотрицательной функцией на отрезке [a;b], а F представляет собой ее первообразную на этом интервале, площадь соответствующей криволинейной трапеции будет определяться как приращение первообразной на интервале [a;b].

Теорему можно записать в таком виде:

Полученное выражение можно представить с помощью графика:

Доказательство теоремы

Доказать утверждение можно путем последовательных действий. Сначала требуется на интервале [a;b] зафиксировать х и найти площадь фигуры, которая расположены под кривой на отрезке [a;х]. Таким образом, каждому х соответствует S(х), и получится новая функция:

Таким образом, площадь криволинейной трапеции будет определяться, как приращение любой первообразной на интервале [a;b].

Формула Ньютона-Лейбница

Функция y = f (x) является непрерывной в интервале [a;b]. Непрерывную функцию можно представить на графике:

Свойства определенного интеграла

Определенный интеграл обладает рядом характерных свойств:

Как найти площадь криволинейной трапеции при помощи интеграла

В качестве примера можно рассмотреть определенный интеграл:

В данном случае:

С помощью геометрической интерпретации можно определить площадь криволинейной трапеции:

Пусть дана функция y = f(x) на отрезке [a, b], причем f / (x) ≥ 0 для любого .

Задача. Найти площадь фигуры ABCD (криволинейная трапеция)

Фигура разбивается на n прямоугольников, ширина которых , высота – .

Тогда приближенно площадь каждого прямоугольника:

Просуммировав площади всех прямоугольников, получим приближенное значение площади искомой фигуры:

(1)(интегральная сумма)

Величина Δ x – шаг разбиения. При уменьшении шага разбиения Δ x → 0, т.е. количество разбиений n → ∞. При этом формула (1) станет более точной. Тогда точное значение площади – предел (если он существует).

Определение.Если последовательность интегральных сумм S _n при n → ∞ имеет конечный предел, не зависящий от способа разбиения отрезка [a, b] и от выбора точки ξ _I , то этот предел называют определенным интегралом функции f(x) в промежутке от a до b.

(2) т.е. интеграл – это сумма

Значения a и b – соответственно нижний и верхний пределы интегрирования. Таким образом, определенный интеграл представляет собой число, а не формулу в отличие от неопределенного интеграла.

1.2. Геометрический смысл определенного интеграла

Если интегрируемая функция , то определенный интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции y = f(x), осью абсцисс и прямыми x=a и x=b,

В этом заключается геометрический смысл определенного интеграла. При этом:

1.3. Свойства определенного интеграла

1) Постоянный множитель можно выносить за знак интеграла: ;

2) О.И. от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов: ;

3) Если , то:

4) Если f(x) ≥ 0 на [a, b], то ; 5) ;

6) Если f(x) ≥ g(x) для любого x из [a, b], то

Площадь фигуры, заключенной между графиками:

(Из функции, график которой лежит выше, вычитается функция, график которой лежит ниже);

7) Теорема о среднем. Если функция f(x) непрерывна на [a, b], то существует такая точка с из [a, b], что: Т.е. площадь криволинейной трапеции может быть найдена как площадь прямоугольника.

1.1. Определенный интеграл как предел интегральных сумм