В чем состоит прием дополнительного построения кратко

Обновлено: 02.07.2024

Свидетельство и скидка на обучение каждому участнику

Зарегистрироваться 15–17 марта 2022 г.

Метод дополнительных построений при решении геометрических задач в курсе планиметрии по учебнику Л.С.Атанасяна.

1)построение прямой, параллельной одной из имеющихся на чертеже;

2) построение прямой, перпендикулярной данной;

3) продолжение медианы;

3) построение окружности.

1.Удвоение медианы треугольника с последующим достраиванием треугольника до параллелограмма, то есть продолжить эту медиану на расстояние равное длине медианы, т.е. продлить ее за точку, лежащую на стороне треугольника. Полученная новая точка соединяется с вершиной (вершинами) исходного треугольника, в результате чего образуются равные треугольники. Равенство соответствующих элементов этих треугольников помогает найти неизвестную величину или доказать предложенное утверждение.

2. Стандартное дополнительное построение в задачах на трапецию: проводим либо два перпендикуляра к основанию и получаем прямоугольник и два прямоугольных треугольника, либо проводим отрезок, параллельно боковой стороне, и получаем параллелограмм и произвольный треугольник, либо проводим через середину меньшего основания прямые, параллельные боковым сторонам, либо продливаем боковые стороны до пересечения . Если же в условии задачи говорится о диагоналях трапеции, то стандартным будет дополнительное построение, состоящее в проведении через одну из ее вершин прямой, параллельной диагонали.

Вспомогательные окружности часто облегчают вычисление углов в задачах о "некруглых" фигурах. Этот метод дополнительного построения можно ввести в 9 классе при повторении и подготовки учащихся к ОГЭ.

Приложение 1.

1.Задачи из учебника Л.С. Атанасяна (№160,165,200, задачи на построение).

2. Докажите, что треугольник является равнобедренным, если совпадают проведенные из одной и той же вершины медиана и биссектриса.

3.В прямоугольном треугольнике АВС (С = 90) проведена медиана СД. Докажите, что СД=ДВ (для проверки усвоения метода)

Приложение 2.

1.Задачи из учебника Л.С. Атанасяна (№384,388,393,527, задачи на построение).

2. Найти среднюю линию трапеции, диагонали которой перпендикулярны и равны 6 и 8.

3. Найдите площадь трапеции с основаниями 6 и 7 и диагоналями 5 и 12.

4. Найдите площадь трапеции, если её диагонали равны 17 и 113, а высота равна 15.

5. В трапеции АВСD ВС II AD M N- середины оснований ВС и AD. АС=√15, ВD=1, MN=2. Найдите площадь трапеции.

6.Вычислить площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные - 17 и 25.

7.Длины боковой стороны AD и основания CD трапеции ABCD равны 2, а длина основания АВ равна 4. Длина диагонали АС равна √7. Найти длину боковой стороны ВС.

8. Отрезок, соединяющий середины оснований трапеции, равен 3. Углы при большем основании равны 30 0 и 60 0 , Найдите высоту,

9. В трапеции длина средней линии равна 4, а углы при одном из оснований имеют величины 400 и 500 . Найти длины оснований трапеции, если длина отрезка, соединяющего середины этих оснований, равна 1. 10. Найдите косинус острого угла равнобедренной трапеции, основания которой равны 37 и 49, а боковые стороны равны 15.

Приложение3.

1.Из точки Р, расположенной внутри острого угла с вершиной А, опущены РВ и РС на стороны угла. Известно, что СВР=25 0 . Найдите угол САР.

2.В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О.

3.В трапеции АВСD с основаниями АD и ВС угол АВD равен углу АСD. Доказать, что АВСD – равнобедренная трапеция.

4.Известно, что ВМ и С N – высоты треугольника АВС, при этом М N =10, и ВС =26. Найдите расстояние между серединами отрезков М N и ВС.

5.В выпуклом четырехугольнике АВСД известно, что _{ВСД= 80} 0 _{, АСВ=50} 0 _{и АДВ=30} 0 _{. Найдите} АДВ.

6. В выпуклом четырехугольнике АВСD АВД = АСД = 45 0 , ВАС = 30 0 , ВС=1. Найдите АД. 7. В треугольнике АВС проведена высота ВК. Найти длину отрезка, соединяющего точку К с серединой АВ, если АВ = 10 см.

Почти любая геометрическая задача решается получением следствий из условий, но есть такие задачи, в которых требуется выполнить дополнительное построение. И тут возникает целая куча проблем. Во-первых, строить можно не всё. Во-вторых, как понять, что именно строить. А в-третьих, как вывести детей на это дополнительное построение?

С первым пунктом всё более-менее понятно. Есть задачи на построение: построение перпендикуляра к отрезку, середины отрезка, биссектрисы угла и т.д. Если это можно построить с помощью циркуля и линейки, значит это может быть дополнительным построением. Тут всё решается наличием или отсутствием знаний. Соответственно, для того, чтобы решить вторую проблему, нужно просто выбрать из возможных вариантов подходящий.

Но вот с третьим вопросом так просто не выйдет. В простых задачах, я говорю детям, что если у них закончились условия и следствий больше получить неоткуда, а задача не решается, то можно попробовать дополнительное построение. Но в таких задачах обычно, нужно просто соединить две точки отрезком. А вот если задача сложная. Тут в общем-то тот же принцип - нехватка условий, нужна еще какая-то информация. Но здесь ее сложнее увидеть, потому что в сложных задачах обычно очень много информации и всю ее перебрать довольно трудно.

Давайте посмотрим, как это может быть на примере.

Условий в задаче не так много, получить из них какие-то выводы будет проблематично, поэтому думаем о том, как найти то, что нужно найти. Если мы говорим об отношениях, то чаще всего думать нужно в сторону подобных треугольников. У нас есть равные вертикальные углы. Попробуем получить еще одну пару равных углов. Равные углы мы встречаем, когда говорим о равных фигурах или о параллельных прямых. Вот мы и нашли наше дополнительное построение. Проведем прямую через точку В параллельно АС.

Таким образом, получаются подобные треугольники BFE и AEM. Но кроме того, подобными будут треугольники BFK и AKC. Именно они и помогут найти нужное отношение.

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Дополнительные построения занимают важное место среди различных методов решения геометрических задач. Например, теорема о площади треугольника, теорема Пифагора, теорема о пересечении высот треугольника и многие другие. При подготовке к экзамену по математике большинство задач по планиметрии не решается с помощью строгих алгоритмов, почти каждая геометрическая задача требует своего подхода.

Искусство решать задачи основывается на хорошем знании теории, на знании достаточного количества геометрических фактов и в овладении приёмами и методами решения.

Эти методы обладают некоторыми особенностями:

большое разнообразие, трудность формального описания, взаимозаменяемость, отсутствие чётких границ области применения.

При решении геометрических задач используются три основных метода:

геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других - алгебраическим.

Во многих случаях решать задачи помогает введение в чертеж дополнительных линий - так называемые дополнительные построения. Такие дополнительные построения, вводящие новые углы и новые отрезки, иногда приводят к появлению геометрических фигур, облегчающих решение задачи. Представленные данные говорят об актуальности изучения метода дополнительных построений.

Объект исследования: планиметрические задачи

Предмет исследования: метод дополнительных построений

·выяснить, в чем состоит суть метода дополнительных построений;

узнать, при решении каких задач целесообразно использовать метод дополнительных построений.

выявить, при решении каких задач метод дополнительных построений является наиболее эффективным;
изучить разнообразные методы, которые могут быть успешно применены при решении многих геометрических задач;
провести группировку различных видов дополнительного построения;

В процессе работы я использовала следующие методы исследования:

анализ математической и методической литературы;
анализ геометрических задач, которые предлагались на ЕГЭ и ОГЭ;
классификация дополнительных построений;
математическое моделирование;

-поиск рационального способа решения задачи методом дополнительного построения.

Теоретическая значимость: исследовательская работа позволяет расширить знания о методе дополнительных построений при решении геометрических задач.

Практическая значимость работы заключается в возможности использования ее результатов учениками, учителями математики.

Решение геометрической задачи начинается с работы над чертежом. Часто на чертеже, особенно в геометрических задачах, которые предлагаются на различных олимпиадах, трудно заметить связи между данными и искомыми величинами. В подобных ситуациях решить задачу помогают дополнительные линии, которые проводятся для того, чтобы свести задачу к ранее решенной или более простой задаче. Они позволяют включить в задачу новые фигуры с их свойствами, тем самым увеличить число теорем, которые можно использовать при решении задачи.

Приёмы дополнительного построения, которые используются при решении геометрических задач можно разделить на два вида - это разбиение фигур и дополнение.

проведение в многоугольнике прямой, параллельной одной из имеющихся (или параллельных прямых), что позволяет применять подобие;
разбиение фигуры на части с целью получения треугольника и параллелограмма (в том числе ромба, квадрата), что позволяет применять свойства этих фигур;
проведение перпендикуляров, радиусов окружности в точки касания, высот в трапеции позволяют получить прямоугольные треугольники.

построение параллелограмма, с помощью продления медианы треугольника, что позволяет применять свойства параллелограмма;
построение дополнительного треугольника;
построение вспомогательной окружности с целью применения свойств хорд, касательных и углов, связанных с окружностью.

Рассмотрим дополнительные построения, использование которых целесообразно при решении планиметрических задач, связанных с треугольниками и четырёхугольниками [4].

1.2.1.Построение прямой параллельной одной из имеющихся (или параллельных прямых)

Если в треугольнике известен отрезок АА1, то через точку А1 проводится прямая, параллельная стороне АВ, до её пересечения со стороной АС (рис.1). По теореме о пропорциональных отрезках получаем . Если отрезок АА1 является медианой, то по теореме Фалеса А2 – середина стороны АС.

Если в треугольнике известны два отрезка, проведённые из разных вершин, в том числе биссектриса, высота, или медиана, то через основание одного из них проводится прямая, параллельная данному отрезку, до её пересечения со стороной треугольника (рис. 2, рис.3). Так на рис. 2 прямая КB2 отсекает от треугольника AA1A2 подобный ему треугольник AКB2, а прямая A1A2 – треугольник CA1A2, подобный треугольнику CBB2.

1.2.2.Разбиение фигуры на части для получения треугольника и параллелограмма

Если в треугольнике (рис. 4), параллелограмме (рис. 5) или трапеции (рис. 6, рис. 7) дана биссектриса одного из внутренних углов, то можно построить ромб, две стороны которого лежат на сторонах данного треугольника или четырехугольника, а биссектриса является диагональю. Такое построение позволяет использовать свойства этих фигур.

Проведённые перпендикуляры позволяют получить прямоугольные треугольники и использовать теорему Пифагора, теоремы о подобии треугольников.

Часто в задачах используются такие дополнительные построения как проведение радиусов окружности в точки касания, высот в трапеции.

Так, если в условии задачи известна медиана треугольника, то удвоив её, мы получим параллелограмм (рис.8), что позволит использовать его свойства [8].

В зависимости от содержания задачи такое дополнительное построение можно выполнять и для двух, и для трёх медиан; использовать не весь параллелограмм, а только его части Например, треугольника АА2С (рис. 8).

1.3.2.Дополнительное построение треугольника

В результате построения, выполненного на рис. 9 (АВ2 ||ВС) и рис. 10 (АС||ВА2), появляются две пары подобных треугольников. Так, на рисунке 9 ?AКB2 и ?A1КB; ?AB1B2 и ?CB1B; на рис. 10 ?AКB1 и ?A2КВ; ?AA1C и ?A2A1B подобны.

На рис. 11 и рис 12 (АМ1|| ВС, L1=КМ∩ВС) ? ALМ1 подобен ? BLL1, ? AMM1 подобен ?CML1, ? AКM1 подобен ?КA1L1.

дополнительные построения - один из основных приемов при решении задач по геометрии.

какое- для себя.. . если только- заложить себе в голову сведения о правильности таких шагов. .

Не можно, а нужно если это облегчает решение ))) И не для себя, а для решения )) Что значит для себя ?

Будут более конркетные вопросы - пиши в агент.

Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.

Проанализируем экзаменационные и олимпиадные задачи, чтобы понять, как использовать нетривиальные, неочевидные подходы.

Задачи с окружностями

С помощью дополнительного построения окружности часто решаются задания № 24 и № 26 ОГЭ, а также № 16 ЕГЭ.

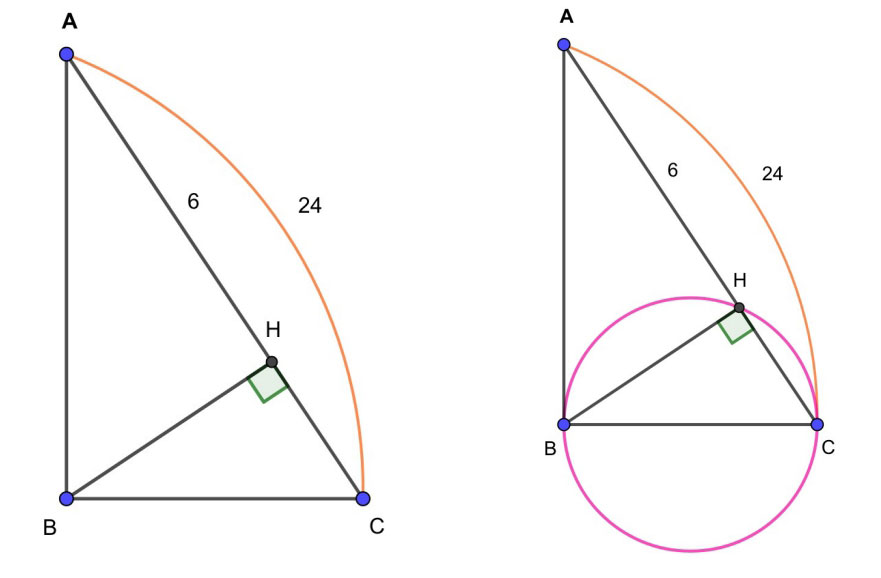
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.

Строим окружность вокруг треугольника ВНС. Центр этой окружности является и серединой ВС. ВС — диаметр. АС по отношению к данной окружности — секущая. АВ — отрезок касательной. АН — внешняя часть секущей. Все это подводит к теореме о квадрате касательной.

Новый справочник содержит весь теоретический материал по курсу математики, необходимый для сдачи основного государственного экзамена в 9 классе. Он включает в себя все элементы содержания, проверяемые контрольно-измерительными материалами, и помогает обобщить и систематизировать знания и умения за курс средней (полной) школы.

Задачи с несколькими вариантами дополнительного построения

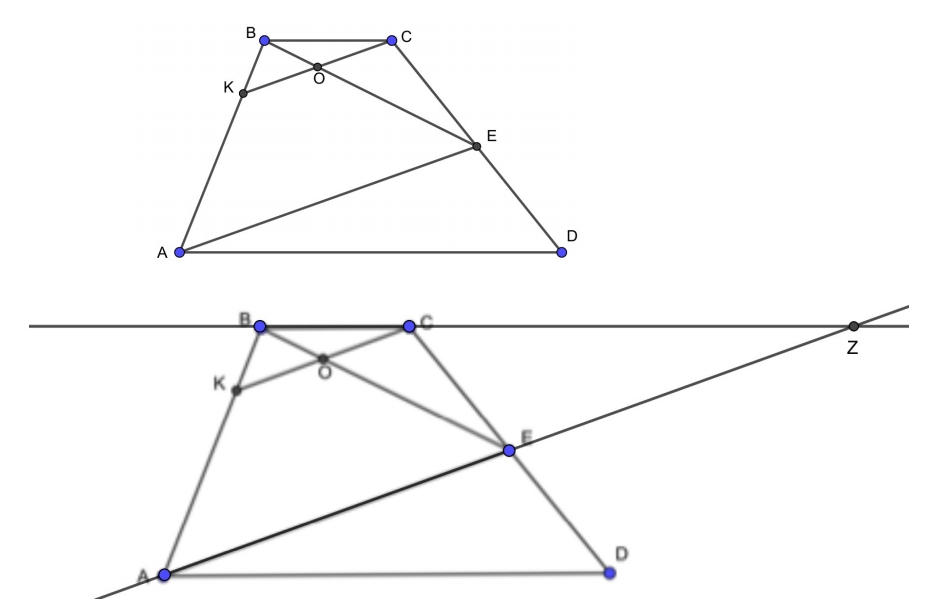
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO=KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

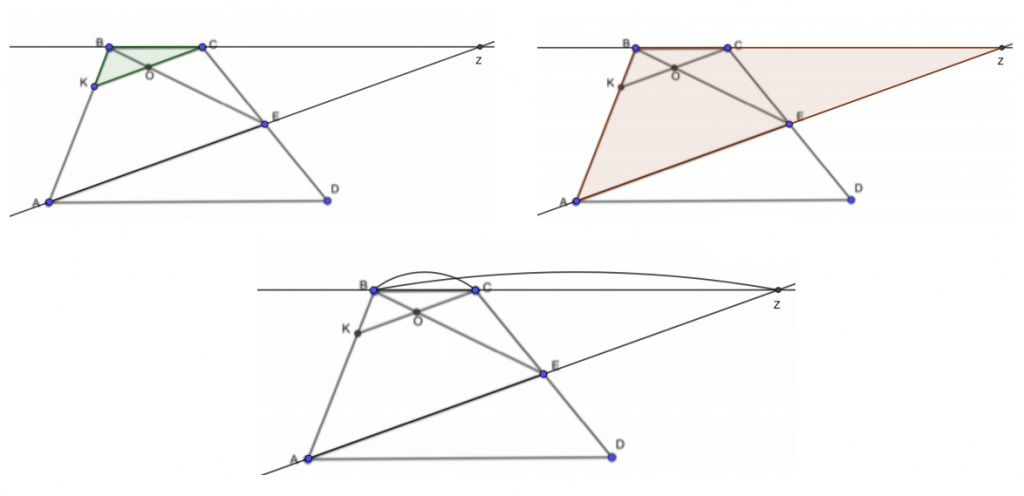
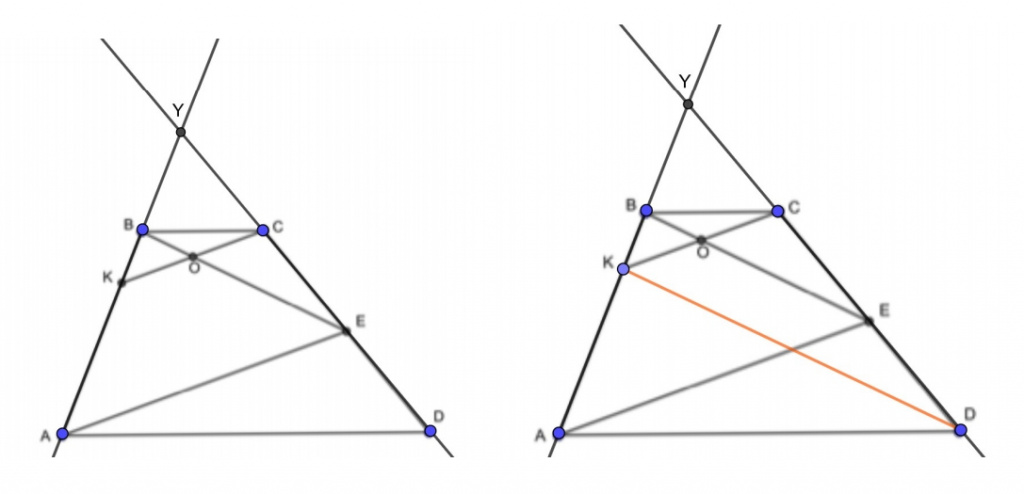
Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO.

Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

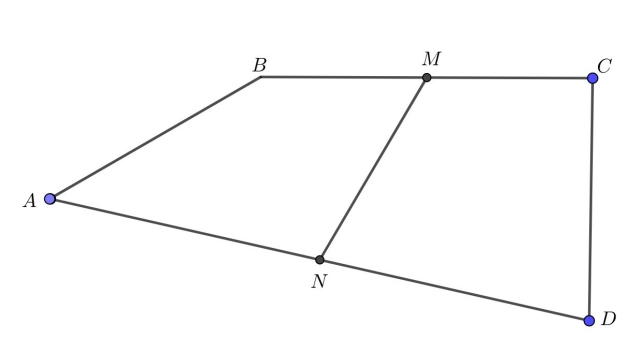
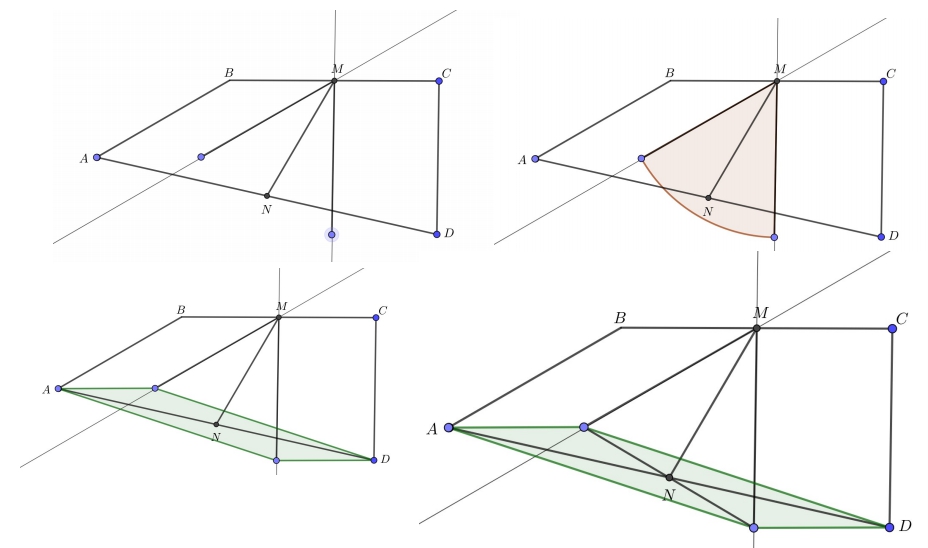
Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Начинаем компоновку данных с точки М и проводим через нее две прямые, параллельные АВ и CD. Далее от точки М откладываем отрезки, равные АВ и, соответственно, CD. Так получается заготовка для равнобедренного треугольника. Нужно понять, будет ли точка N лежать на отрезке, соединяющем две новые точки. Строятся новые отрезки, равные и параллельные ВМ и МС — получается четырехугольник-параллелограмм. AD является диагональю этого параллелограмма, а N — серединой диагонали. Также N лежит и на другой диагонали. Равнобедренный треугольник готов. Угол с вершиной M в нем равен 60°. Треугольник равносторонний, MN является медианой и биссектрисой. MN, пресекаясь с BC, образует угол, равный 60°.

Читайте также: