Почему в реальном колебательном контуре колебания будут затухающими кратко

Обновлено: 04.07.2024

Рассмотренные в предыдущих разделах цепи переменного тока наводят на мысль, что пара элементов – конденсатор и катушка индуктивности образуют своеобразную колебательную систему. Сейчас мы покажем, что это действительно так, в цепи состоящей только из этих элементов (рис. 262) возможны даже свободные колебания, то есть без внешнего источника ЭДС. Поэтому цепь (или часть другой цепи), состоящая из конденсатора и катушки индуктивности называется колебательным контуром.

Пусть конденсатор зарядили до заряда q₀ и затем подключили к нему катушку индуктивности. Такую процедуру легко осуществить с помощью цепи, схема которой показана на рис. 263: сначала ключ К замыкают в положении 1, при этом конденсатор заряжается до напряжения, равного ЭДС источника, после чего ключ перебрасывают в положения 2, после чего начинается разрядка конденсатора через катушку.

В этом уравнении содержится две неизвестных функции – зависимости от времени заряда q(t) и силы тока I(t), поэтому его решить нельзя. Однако сила тока является производной от заряда конденсатора q′(t) = I(t), поэтому производная от силы тока является второй производной от заряда

С учетом этого соотношения, перепишем уравнение (1) в виде

Поразительно, но это уравнение полностью совпадает с хорошо изученным нами уравнением гармонических колебаний (вторая производная от неизвестной функции пропорциональна самой этой функции с отрицательным коэффициентом пропорциональности $x'' = -\omega^2_0 x$)! Следовательно, решением этого уравнения будет гармоническая функция

$~q = A \cos (\omega_0 t + \varphi)$ (4)

с круговой частотой

Эта формула определяет собственную частоту колебательного контура. Соответственно период колебаний заряда конденсатора (и силы тока в контуре) равен

Полученное выражение для периода колебаний называется формулой Дж. Томпсона.

Как обычно, для определения произвольных параметров A, φ в общем решении (4) необходимо задать начальные условия – заряд и силу тока в начальный момент времени. В частности, для рассмотренного примера цепи рис. 263, начальные условия имеют вид: при t = 0 q = q₀, I = 0, поэтому зависимость заряда конденсатора от времени будет описываться функцией

$~q = q_0 \cos \omega_0 t$ , (7)

а сила тока изменяется со временем по закону

$~I = - \omega_0 q_0 \sin \omega_0 t$ . (8)

Следует отметить, что приведенное рассмотрение колебательного контура является приближенным – любой реальный контур обладает активным сопротивлением (соединительных проводов и обмотки катушки). Поэтому в уравнении (1) следует учесть падение напряжения на этом активном сопротивлении, поэтому это уравнение приобретет вид

который с учетом связи между зарядом и силой тока, преобразуется к форме

Это уравнение нам также знакомо – это уравнение затухающих колебаний $x'' = -\omega^2_0 x - \beta x'$, причем коэффициент затухания, как и следовало ожидать, пропорционален активному сопротивлению цепи $~\beta = \frac$.

Процессы, происходящие в колебательном контуре, могут быть также описаны и с помощью закона сохранения энергии. Если пренебречь активным сопротивлением контура, то сумма энергий электрического поля конденсатора и магнитного поля катушки остается постоянной, что выражается уравнением

которое также является уравнением гармонических колебаний с частотой, определяемой формулой (5). По свое форме это уравнение также совпадает уравнениями, следующими из закона сохранения энергии при механических колебаниях. Так как, уравнения, описывающие колебания электрического заряда конденсатора, аналогичны уравнениям, описывающим механические колебания, то можно провести аналогию между процессами, протекающими в колебательном контуре, и процессами в любой механической системе.

Пользуясь этой аналогией, качественно опишем процесс колебаний заряда и электрического тока в контуре. В начальный момент времени конденсатор заряжен, сила электрического тока равна нулю, вся энергия заключена в энергии электрического поля конденсатора (что аналогично максимальному отклонения маятника от положения равновесия). Затем конденсатор начинает разряжаться, сила тока возрастает, при этом в катушке возникает ЭДС самоиндукции, которая препятствует возрастанию тока; энергия конденсатора уменьшается, переходя в энергию магнитного поля катушки (аналогия – маятник движется к нижней точки с возрастанием скорости движения). Когда заряд на конденсаторе становится равным нулю, сила тока достигает максимального значения, при этом вся энергия превращается в энергию магнитного поля (маятник достиг нижней точки, скорость его максимальна). Затем магнитное поле начинает убывать, при этом ЭДС самоиндукции поддерживает ток в прежнем направлении, при этом конденсатор начинает заряжаться, причем знаки зарядов на обкладках конденсатора противоположны начальному распределению (аналог – маятник движется к противоположному начальному максимальному отклонению). Затем ток в цепи прекращается, при этом заряд конденсатора становится опять максимальным, но противоположным по знаку (маятник достиг максимального отклонения), после чего процесс повторятся в противоположном направлении.

18.8.2 Вынужденные колебания в контуре.

Чтобы явным образом показать, что явление резонанса напряжений можно рассматривать как вынужденные колебания, перепишем использованное уравнение закона Ома

$~\varepsilon(t) = U_R(t) + U_C(t) + U_L(t)$ .

Для чего подставим в него явные выражения для напряжений на элементах цепи $~U_C = \frac$ , $~U_R = IR = Rq'$ , $~U_L = -\varepsilon_ = LI' = Lq''$ и ЭДС источника $\varepsilon = U_0 \cos \omega t$:

$~Lq'' + \frac + Rq' = U_0 \cos \omega t$

и перепишем его в виде

$~q'' = -\frac q - \frac q' + \frac \cos \omega t$ ,

который полностью совпадает с уравнением вынужденных колебаний $x'' = -\omega^2_0 x - \beta x' + f_0 \cos \omega t$.

Рассмотрим теперь возможность возникновения вынужденных колебаний в контуре, когда источник переменной ЭДС находится вне контура [2] , как показано на рис. 266. Расчет данной цепи проведем, используя метод векторных диаграмм (которая также представлена на рис. 266). В данном случае нас, прежде всего, будет интересовать сила тока в колебательном контуре.

Так как конденсатор и катушка индуктивности соединены параллельно, то мгновенные напряжения (U_C, U_L) на этих элементах одинаковы. Обозначим это напряжение U₁. Построение диаграммы следует начинать с построения вектора, изображающего колебания этого напряжения. Далее построим векторы, изображающие колебания сил токов через конденсатор I_C и катушку индуктивности I_L - эти векторы перпендикулярны вектору напряжения U₁ и противоположны друг другу. Как обычно, колебания токов через конденсатор и через катушку индуктивности происходят в противофазе. Колебательный контур соединен последовательно с резистором, поэтому сумма токов I_C и I_L (конечно, их мгновенных значений) равна силе тока через резистор I_R. Вектор изображающий напряжение на резисторе U_R, сонаправлен с вектором суммарного тока. Наконец сумма векторов напряжения на резисторе U_R и напряжения на контуре U₁ равна ЭДС источника.

Построенная векторная диаграмма позволяет рассчитать амплитудные значения токов и напряжений на элементах данной цепи. Выразим традиционным образом амплитудные значения сил токов через конденсатор и катушку через амплитуду напряжения на контуре

Амплитуда силы тока через резистор (и через источник) определяется из векторной диаграммы и равна

$~I_ = (I_ - I_) = U_ \left( \omega C - \frac <\omega L>\right)$ . (2)

Теперь можно записать выражение для амплитуды напряжения на резисторе

$~U_ = I_R = U_ \left( \omega C - \frac <\omega L>\right) R$ . (3)

Далее, глядя на диаграмму напряжений, запишем теорему Пифагора для вектора ЭДС источника ⎟ ⎟

$~U^2_0 = U^2_ + U^2_ = U^2_ \left( 1 + \left( \omega C - \frac <\omega L>\right)^2 R^2 \right) = U^2_ R^2 \left( \frac + \left( \omega C - \frac <\omega L>\right)^2 \right)$ , (4)

здесь U₀ - амплитуда ЭДС источника.

Из этого уравнения легко определить напряжение на резисторе

Наконец, с помощью формул (1), (2), (3), запишем выражения для сил токов в рассматриваемой цепи

Проанализируем зависимость этих величин от частоты источника ЭДС. Во всех формулах под корнем имеется два положительных слагаемых, причем только второе зависит от частоты. При частоте

равной собственной частоте колебательного контура второе слагаемое под корнем обращается в ноль, поэтому можно ожидать, что вблизи этой частоты силы токов через конденсатор и катушку достигают максимального значения. Понятно, что максимумы функций I_L0(ω) и I_C0(ω) несколько смещены от частоты ω₀, потому, что частота источника ω присутствует и вне корня. Однако, если первое слагаемое под корнем ($\frac$), мало, то сдвиг максимума от значения ω = ω₀ будет незначительным. Отметим, также, что при $~\omega = \omega_0 = \frac>$ амплитуды токов через конденсатор и катушку оказываются равными. Действительно, в этом случае

Но самое неожиданное, что при ω = ω₀ сила тока через резистор обращается в нуль! Соответственно, напряжение на колебательном контуре становится равным ЭДС источника, что также следует и из полученных формул для токов в контуре. Схематические графики зависимостей [3] амплитуд токов от частоты источника показаны на рис.267. Понятно, что при ω → 0 и ω → ∞ сопротивление контура стремится к нуля и в этом случае сила тока через резистор стремится к своему предельному значению $~I_ = \frac$.

Таким образом, мы показали, что в рассмотренной цепи при частоте источника стремящейся к собственной частоте контура амплитуда силы тока в контуре резко возрастает, наблюдается явление резонанса, следовательно, колебательный контур можно использовать для выделения колебаний требуемой частоты. Интересно, отметить, что острота пика возрастает с ростом сопротивления резистора, находящегося вне контура.

В заключение данного раздела, обсудим, почему при ω = ω₀ сила тока во внешней для контура цепи обращается в нуль. Колебания токов через конденсатор I_C и через катушку индуктивности происходят в противофазе I_L, а в случае ω = ω₀ амплитуды этих токов сравниваются, в результате чего формально и получается нулевое значение для суммарного тока. Фактически в этом случае электрический ток циркулирует в колебательном контуре, не выходя из него. Подчеркнем, что наш анализ проведен для установившегося режима колебаний – в переходном режиме ток через резистор (и через источник идет) обеспечивая контур энергией. Когда колебания установятся, подкачка энергии становится излишней, так как мы пренебрегли потерями энергии в контуре. Обратите внимание, что при ω = ω₀ сила тока в контуре не зависит сопротивления внешнего резистора, а полностью определяется параметрами контура.

Вспомните, что вынужденные колебания механических систем обладают тем же свойством – при точном резонансе и при отсутствии сил сопротивления работа внешней силы также обращается в нуль.

Если же рассмотреть реальный контур, обладающий активным сопротивлением, то между током в контуре и напряжением на нем разность фаз будет отлична от нуля, поэтому энергия источника будет поступать в контур, компенсируя потери. В этом случае также будет отличен от нуля и ток во внешней цепи.

Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, - затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = - k x - y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e - период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C - собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C - сопротивление, индуктивность, емкость, а ω 0 - частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( - β t ) cos ω t + a ' 0 = q 0 e - β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

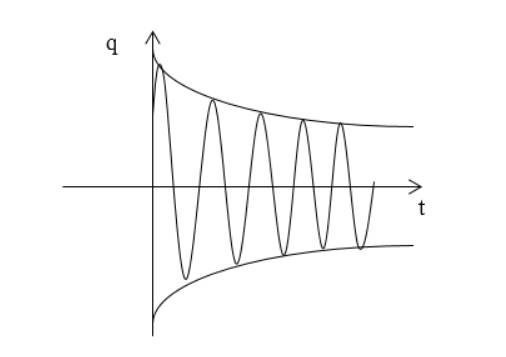
Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту - ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C - контуре:

q ( t ) = q 0 e ( - β t ) cos ω t + a ' 0 = q 0 e - β t cos ( ω t ) .

Предположим, что при t = 0 , a ' 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = - ω 0 q 0 e ( - 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( - 2 β t ) cos 2 ( ω t ) = W 0 e ( - 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( - 2 β t ) sin 2 ω t + a = W 0 e - 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( - 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( - 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( - 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( - 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( - 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( - 2 β t ) . Энергия в контуре убывает по экспоненте.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

Соотношение (1) применяется при решении многих задач.

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Гармонический закон колебаний в контуре

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Сила тока считается положительной 0)' alt='(I > 0)' /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0' alt='I > 0' /> , то заряд левой пластины возрастает, и потому 0' alt='\dot > 0' /> .

Величины и меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):

Подставляя сюда и , получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.

Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.

Затухающие колебания характеризуют коэффициентом затухания ($\beta $), равным:

Из выражения (1) видно, что $\beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($\delta $), который равен:

где $a\left(t\right)$- амплитуда какой -- либо величины (заряда, силы тока и т.д.). $\delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:

Для $RLC$ контура:

где $\omega $ -- частота.

Если затухание небольшое ($\delta \ll 1$), то полагают, что $\beta \ll <\omega >_0$ ($<\omega >_0=\sqrt>-собственнная\ частота$), тогда $\omega \approx <\omega >_0$. В таком случае:

Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:

Для слабого затухания добротность можно выразить как:

Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:

где $W$ -- энергия контура, $\triangle W$- уменьшение энергии контура за одно колебание.

Готовые работы на аналогичную тему

Уравнение затухающих колебаний

Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:

где $\omega =\sqrt-\frac> \cdot \beta =\frac$. Амплитуда равна:

В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:

Начальная фаза колебаний ($_0$) равна:

При $R >2\sqrt>$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.

Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:

График функции (10) изображают как на рис.2.

Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $\beta $. Собственная частота $<\omega >_0.\ $

Решение:

В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:

в выражении (1.1) мы предположили, что при $t=0,\ '>_0=0$. Используя выражение:

Найдем $I(t)$, получим:

Следовательно, электрическая энергия контура ($W_q$) имеет вид:

Магнитная энергия контура ($W_m$) равна:

Полная энергия равна:

Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.

Решение:

Если колебания в контуре затухают медленно, то это значит:

Следовательно, выражение для энергии, запасенной в контуре:

можно преобразовать к виду:

Ответ: $W\left(t\right)=W_0e^<\left(-2\beta t\right)>$. Энергия контура убывает по экспоненте.

Читайте также: