Отдельным видом каких выражений являются рациональные дроби кратко

Обновлено: 04.07.2024

Рациональная дробь (рациональная функция) -- это отношение двух многочленов $P_ (x)$ и $Q_ (x)$ степеней $m$ и $n$ соответственно:

Дробь $\frac (x)> (x)> $ называется правильной рациональной дробью, если $m

В случае, когда имеется неправильная рациональная дробь, то ее можно представить в виде суммы некоторого многочлена и правильной дроби путем деления числителя на знаменатель по правилу деления многочленов:

Определить тип рациональной дроби. В случае неправильной дроби выполнить деление.

Так как степень числителя больше степени знаменателя, то имеем неправильную дробь.

Разделим числитель на знаменатель и получим:

Правильные рациональные дроби вида:

называются простейшими дробям I, II, III и IV типов.

Определить тип простейшей рациональной дроби:

1) $\frac $ - рациональная дробь I типа (по определению 3);

2) $\frac +x+3> $- рациональная дробь III типа (по определению 3);

3) $\frac <(x^<2>+x+3)^ > $- рациональная дробь IV типа (по определению 3);

4) $\frac > $ - рациональная дробь II типа (по определению 3).

Готовые работы на аналогичную тему

Рассмотрим интегрирование рациональных дробей I, II и III типов в общем виде.

Интегрирование дробей I типа:

\[\int \frac dx =3\cdot \int \frac =3\cdot \ln |x-1|+C\]

Интегрирование дробей II типа:

Интегрирование дробей III типа:

Интегрирование дробей IV типа:

Для вычисления первого интеграла используется подстановка

Вычислим второй интеграл. Обозначим его через $I_ $ и запишем в виде

Далее преобразуем последний интеграл:

Интегрируя по частям, получаем:

Подставим в выражение выше равенство (1) и получим:

В правой части имеется интеграл того же типа, что и $I_ $ с показателем степени знаменателя подынтегральной функции на 1 ниже $k-1$. Следовательно, интеграл $I_ $ выразили через $I_ $.

Продолжая дальше, получим:

Подставляя везде вместо $t$ и $m$ их значения, получим выражение интеграла IV типа через $x$ и заданные числа $A,B,p,q$.

К последнему интегралу применим следующую подстановку $x+1=t$:

(примечание: произвольная постоянная будет учтена в записи окончательного результата)

Поурочное планирование по алгебре для 8 класса. Ориентировано на работу с УМК Макарычев. Алгебра 8 класс. Просвещение. Глава 1. Рациональные дроби. § 1. Рациональные дроби и их свойства (5 ч). Уроки 1-2. Рациональные выражения. Вернуться к Списку уроков Тематического планирования.

Уроки 1-2. Рациональные выражения

Цель: рассмотреть рациональные выражения и допустимые значения переменных в них.
Планируемые результаты: освоить виды алгебраических выражений, понятие допустимых значений переменных.
Тип уроков: уроки общеметодологической направленности.

ХОД УРОКОВ

II. Работа по теме уроков

План уроков

Виды алгебраических выражений.
Допустимые значения переменных в выражении.

1. Виды алгебраических выражений

Напомним основные понятия, введенные в 7 классе. Алгебраическим выражением называется выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления, возведения в степень и с помощью скобок.

Пример 1

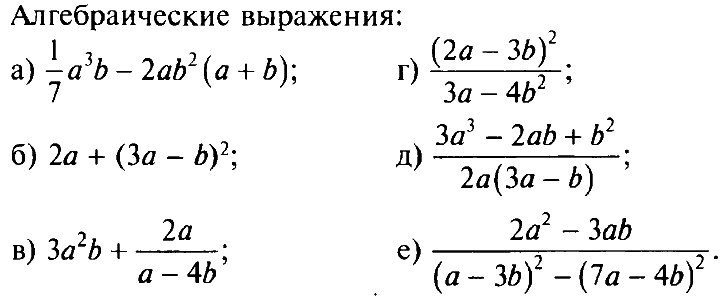
Алгебраическое выражение, которое не содержит деления на выражения с переменными, называется целым. В примере 1 целыми являются выражения а и б. Выражение, которое содержит деление на переменные, называется дробным. В примере 1 дробными являются выражения в—е. Целые и дробные выражения вместе называются рациональными. После преобразований целые выражения можно подразделить на одночлены и многочлены.

Пример 2

Рациональное выражение, представляющее собой дробь, числитель и знаменатель которой многочлены, называется рациональной дробью. При этом одночлены считаются частным видом многочленов.

Пример 3

а) Рациональные дроби:

б) Рациональные выражения

не являются рациональными дробями (по определению), так как в первых двух случаях выражения не являются дробью, в третьем случае числитель дроби будет многочленом только после преобразований, в четвертом случае знаменатель дроби станет многочленом также только после преобразований.

Разумеется, принципиальных отличий рационального выражения от рациональной дроби не существует. После соответствующих преобразований рациональное выражение можно привести к рациональной дроби. В примере 3, б в первом случае достаточно привести подобные члены, во втором случае привести выражения к общему знаменателю, в третьем случае числитель возвести в квадрат, в четвертом случае знаменатель возвести в куб.

2. Допустимые значения переменных в выражении

Значения переменных, при которых алгебраическое выражение имеет смысл, называются допустимыми значениями переменных. Целое выражение имеет смысл при любых значениях, входящих в него переменных, так как все действия с переменными выполнимы.

Пример 4

Пример 5

III. Задания на уроках

№ 2; 3; 4 (а); 5 (б); 7 (а); 9 (б); 10 (б); 12; 14; 15 (а); 17 (а); 18 (а, б); 19 (а).

IV. Контрольные вопросы

Какое выражение называется алгебраическим? Приведите примеры.
Дайте определение целого и дробного выражений. Приведите примеры.
Вспомните понятия одночлена и многочлена (курс 7 класса). Приведите примеры.
Какое выражение называется рациональной дробью? Приведите примеры.
Какие значения переменных называются допустимыми?
При каких значениях переменных целое выражение имеет смысл?
При каком условии дробное выражение не имеет смысла? Приведите примеры.

V. Подведение итогов уроков

Домашнее задание: № 1; 4 (б); 5 (а); 7 (б); 8 (а); 9 (а); 10 (а); 11; 13; 15 (г); 16(6, в); 17(6); 19 (б).

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). Глава 1. Рациональные дроби. § 1. Рациональные дроби и их свойства (5 ч). Уроки 1-2. Рациональные выражения. Вернуться к Списку уроков Тематического планирования.

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.

Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла

при а = 0. При всех остальных значениях а это выражение имеет

смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Выражение вида равно нулю ?

Дробь . Итак, числитель дроби равен нулю при x = 7 и x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит, данная дробь равна нулю при x = 7.

2. Основное свойство дроби. Сокращение дробей

Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство

На основании сочетательного и переместительного свойств умножения имеем:

Так как bс ≠ 0, то по определению частного

Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.

Равенство (1) выражает основное свойство рациональной дроби:

если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.

Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.

Пример 1. Приведем дробь к знаменателю

Так как , получим:

если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Отдельным видом каких выражений являются рациональные дроби.

Отдельным видом рационального выражения является рациональная дробь - ее числитель и знаменатель состоят из многочлена.

Выразите рациональную дробь в виде десятичной дроби с выраженным периодом?

Выразите рациональную дробь в виде десятичной дроби с выраженным периодом.

Значение какого из выражений является числом рациональным?

Решите пожалуйста и какое из выражений является рациональным?

Начение какого из выражений не является рациональным числом?

Начение какого из выражений не является рациональным числом.

Значение какого из выражений является рациональным числом?

Представьте выражение в виде рациональной дроби?

Представьте выражение в виде рациональной дроби.

Представьте выражение (х ^ - 1 - у ^ - 1)(х - у) ^ - 1 в виде рациональной дроби?

Представьте выражение (х ^ - 1 - у ^ - 1)(х - у) ^ - 1 в виде рациональной дроби.

Объясните, как решать?

Какую дробь можно назвать рациональной?

Представьте в виде рациональной дроби выражение : 1.

СРОЧНО?

Представьте выражение (а / б - б / а) ^ 2 в виде рациональной дроби.

Подайте в виде дроби выражения ?

Подайте в виде дроби выражения .

Помогите решить рационально.

Можно найти площадь по формуле Герона Т. К. большая высота лежит напротив меньшей стороны, тогда Ответ : большая высота равна 8 см.

Где вопрос? Что решать? ).

Рассмотрите такой вариант : так как в знаменателе не может быть нуль, а под знаком радикала в числителе - отрицательное число, то d область определения входят все числа, кроме + 1, - 1 и меньшие 5. В итоге x∈[5 ; + oo).

Перенесем все в левую часть и рассмотрим выражение как разность квадратов : D = 1 - 80.

Решение смотри на фото.

1)810÷25 = 32. 4 - 32грузовиков потребуется 2)32 + 1 = 33(г) - потребуется для перевозки всех мешков Ответ : 33грузовика По мне так.

Выучи те правила которые написаны.

3xy - 2z = 4 1 : (3xy - 2z) = 0, 25.

Хорошо воспользоваться теоремой Виета. Сумма корней а и b равна 1, а произведение a * b = - 5. A ^ 3 + b ^ 3 = (a + b) * (a ^ 2 - ab + b ^ 2) = (a + b) * ((a + b) ^ 2 - 3ab) = 1 * (1 + 3 * 5) = 16 Примечание : Когда пользуемся теоремой Виета неплох..

Читайте также: