Объясните как определяется координаты точки в пространстве кратко

Число х называется абсциссойточки М, у – ординатой, а z – аппликатой точки М. Записывается это следующим образом: М(x,y,z). Другими словами, координатами точки М в системе (О ) называются координаты её радиус −вектора в базисе данного репера R=(О, ).

Если аппликата z точки М равна нулю, то из равенства (1) получаем:

Векторы , , линейно зависимы, поэтому они компланарны. Это означает, что точка М лежит в плоскости Оху. Из предыдущего равенства следует, что в плоскости (Оху) т. М в системе координат (О ) имеет две координаты М(х,у), а в системе координат (О ) эта точка имеет координаты М(x,y,0). Аналогично, если у=0, то М (Оxz) и в системе координат (О ) она имеет координаты М(x,0,z), еслих=0, то М (Оxz) => M(0,y,z). Отсюда следует, что если точка М принадлежит оси абсцисс, то у=z=0 то есть в системе координат (О ) она имеет координаты М(x,0,0), для любой точки оси ординат x=z=0 системе координат (О ) она имеет координаты М(0,у,0), а для любой точки оси аппликат x=y=0 системе координат (О ) она имеет координаты М(0,0,z).

Для построения т. М(x,y,z) по её координатам в системе О воспользуемся формулой (1). От начала координат О отложим вектор = =x , затем от т.М₁ отложим вектор и от точки М₂ отложим (рис.3)

По правилу многоугольника = x + y + z . Таким образом, М – искомая точка. Ломаную называют координатной ломанной т. М. Итак, для построения точки М достаточно построить её координатную ломанную. Каждое звено имеет длину соответствующей координаты, если единицей измерения есть длина соответствующего базисного вектора.

Положение точки в пространстве представим с помощью пространственного макета. Пусть даны в пространстве точка A и три взаимно перпендикулярные плоскости проекции.

Построим проекции точки А, расположенной в первом октанте пространства. Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций . На пересечении этих лучей с плоскостями проекций H, V, W находятся проекции самой точки А (A`, A", A"`).

Положение точки в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые она удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку A провести прямые, перпендикулярные к плоскостям проекций, определить точки A`, A", A"` встречи этих прямых с плоскостями проекций и измерить величины отрезков [AA`], [AA"], [AA"`], которые укажут соответственно значение аппликаты z, ординаты y, абсциссы x точки A.

Точки A`, A", A"` называют ортогональными проекциями точки A, при этом согласно принятым обозначениям: A` – горизонтальная проекция точки A; A" – фронтальная проекция точки A; A"` – профильная проекция точки A.

Прямые (AA` ⊥ H), (AA" ⊥ V), (AA"` ⊥ W) называют проецирующими прямыми или проецирующими лучами. Прямую (AA`), проецирующую точку A на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой (лучом). Прямую (AA") проецирующую точку A на фронтальную плоскость проекций называют фронтально проецирующей прямой (лучом). Прямую (AA"`) проецирующую точку A на профильную плоскость проекций называют профильно-проецирующей прямой (лучом). Две проецирующие прямые, проходящие через точку A, определяют плоскость, которую принято называть проецирующей.

Чтобы получить эпюр точки A, выполним преобразование пространственного макета в эпюр Монжа: – фронтальная проекция точки A остается на месте, как принадлежащая плоскости V, которая не меняет своего положения при рассматриваемом преобразовании. – горизонтальная проекция A` вместе с горизонтальной плоскостью проекции опустится вниз и расположится на одном перпендикуляре к оси x с фронтальной проекцией A". – профильная проекция AA"` будет вращаться вместе с профильной плоскостью проекции и к концу преобразования займет положение, указанное на рисунке. При этом AA"` будет принадлежать перпендикуляру к оси z, проведенному через A" и удалена от оси z на такое же расстояние, на какое горизонтальная проекция A` удалена от оси x.

Связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [A`A<sub>y</sub>] и [A<sub>y</sub>A"`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей. Отмеченной связью пользуются для нахождения недостающей профильной или горизонтальной проекции.

Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями может быть установлена с помощью ломаной линии A`,A<sub>o</sub>,A"` с вершиной A_o на биссектрисе угла, образованного осями y. Биссектрису O,A_o,A"` называют постоянной прямой k_o эпюра Монжа.

Представленная на рисунке плоская модель (эпюр) несет такую же информацию, какая содержится в пространственном макете. Действительно: чтобы определить положение точки в пространстве, необходимо знать три координаты точки A – (x, y, z) – это длины отрезков [AA"`], [AA"], [AA`]. Величины этих отрезков могут быть легко определены на эпюре: [AA"`] ≅ [A`A_y] ≅ [A"A_z]; [AA"] ≅ [A`A<sub>x</sub>] ≅ [A"`A_z]; [AA`] ≅ [A"A<sub>x</sub>] ≅ [A"`A_y].

Горизонтальная проекция точки A определяется абсциссой x и ординатой y Фронтальная проекция – абсциссой x и аппликатой z Профильная проекция – ординатой y и аппликатой z

Из записи следует: 1. Точка в пространстве удалена: а) от плоскости проекции W на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси y (или же фронтальная проекция A" от оси z); б) от плоскости проекции V на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси x (или ее профильная проекция A"` от оси z); в) от плоскости проекции H на такую же величину, на какую ее фронтальная проекция A" удалена от оси x (или ее профильная проекция A"` от оси y).

2. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Как следствие из этого – по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью ортогональную проекцию. Действительно: какое бы сочетание из двух ортогональных проекций мы не взяли, они всегда дают нам значение всех трех координат точки. 3. a) горизонтальная и фронтальная проекции любой точки принадлежат одному перпендикуляру к оси x.

Если принять во внимание, что на эпюре прямые, перпендикулярные к осям проекций и соединяющие разноименные проекции точек, называют линиями связи (проекционной связи), то пункт 3. а) может быть сформулирован иначе: горизонтальная и фронтальная проекции любой точки принадлежат одной линии связи.

б) горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y; в) фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z.

Урок 1. Геометрия 11 класс

Конспект урока "Прямоугольная система координат в пространстве"

Вы уже знакомы с прямоугольной системой координат на плоскости, другими словами прямоугольной координатной плоскостью. Такую систему координат задают две взаимно перпендикулярные прямые, на каждой из которых выбрано направление и величина единичного отрезка. Эти прямые называют осями абсцисс и ординат.

Точку пересечения осей называют точкой начала координат.

Прямоугольную систему координат на плоскости обозначают Оху.

Каждой точке плоскости сопоставляется только одна пара чисел, которые называют её координатами. Для определения координат, из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу и ординату точки.

Если же через точку пространства проведены три попарно перпендикулярные прямые, а на каждой из них выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.

Прямые с выбранными на них направлениями называют осями координат, а точку их пересечения — началом координат. Как и на плоскости её обычно обозначают буквой О.

Оси координат обозначают так: Ох, Оу, Оz. И называют осью абсцисс, осью ординат и, новым является название третьей оси, ось аппликат.

Прямоугольную систему координат в пространстве обозначают Охуz.

Через каждые 2 оси координат проходят координатные плоскости: Оху, Оуz и Охz. Всего таких плоскостей 3.

Каждая ось делится точкой О на два луча. В соответствии с этим, лучи, направление которых совпадает с направлением оси, называют положительными полуосями, а оставшиеся лучи — отрицательными полуосями.

Каждой точке пространства сопоставляется только одна тройка чисел, которые называют её координатами. Их определяют аналогично тому, как это делали на плоскости. Только через точку М проводят плоскости перпендикулярные координатным осям.

Точки пересечения проведённых плоскостей с осями координат назовём М₁, М₂ и М₃.

Первая координата точки М, то есть её абсцисса, равна длине отрезка ОМ₁.

Вторая координата, которую называют ординатой, равна длине отрезка ОМ₂.

Ну, а третья координата, а точнее аппликата, равна длине отрезка ОМ₃.

Координаты точки записывают в скобках, при этом первой записывают абсциссу, второй — ординату, а третьей — аппликату.

В данном случае точки М₁, М₂ и М₃ являются точками положительных полуосей, поэтому и координаты точки М будут положительными числами.

Рассмотрим примеры различного расположения точек в прямоугольной системе координат.

Задание: определить координаты точек А, В, С, D, Е и F.

После выполнения этого задания можно сделать вывод о том, что если точка лежит в некоторой координатной плоскости или на некоторой координатной оси, то её соответствующие координаты будут равны нулю.

Так если точка лежит в координатной плоскости ОИксИгрек, то её аппликата равна нулю. Если точка лежит в координатной плоскости ОИксЗэт, то её ордината равна нулю. И если точка лежит в координатной плоскости ОИгрекЗэт, то её абсцисса равна нулю.

Ну, а в случаях, когда точка лежит на одной из осей, только одна координата является ненулевой.

Так мы с вами нашли координаты проекций точки А на координатные оси и на координатные плоскости.

Решение: Изобразим прямоугольную систему координат. Отметим точки, являющиеся вершинами куба, координаты которых известны.

На этом уроке вы познакомились с понятием прямоугольной системы координат в пространстве. Узнали, что её задают три взаимно перпендикулярные прямые, на которых выбраны направления и единичные отрезки. Эти прямые называют координатными осями. Точку пересечения осей называют точкой начала координат.

Ось Ох называют осью абсцисс, ось Оу называют осью ординат, и новым для вас является название оси Оz — ось аппликат. Помимо осей координат в прямоугольной системе координат присутствуют и координатные плоскости: Оху, Оуz и Охz.

Всю прямоугольную систему координат в пространстве обозначают Охуz.

Любой точке пространства соответствует только одна тройка чисел х, у и z, которые и являются её координатами. Все координаты точки О начала координат равны нулю.

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O . Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.

Прямые с началом O , имеющие направление и масштаб, называют координатной прямой или координатной осью.

Прямоугольная система координат обозначается O x y . Координатными осями называют О х и О у , называемые соответственно ось абсцисс и ось ординат.

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех О х , О у , О z осей. Это три взаимно перпендикулярные прямые, где О z имеет название ось аппликат.

По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке O , называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте О х против часовой стрелки на 90 ° ее положительное направление совпадает с положительным О у , тогда это применимо для положительного направления О z . Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y , а средний за Z .

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку М на координатной оси О х . Любое действительное число x M равняется единственной точке М , расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если – 3 , то соответственное расстояние 3 . Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М , расположенная на O x , равна действительному числу x M . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении O x и О у . Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

Возьмем точку как проекцию точки M x на О х , а как проекцию точки M y на О у . Значит, через точку М можно провести перпендикулярные осям О x и О у прямые, где послучим соответственные точки пересечения M x и M y .

Тогда точка M x на оси О х имеет соответствующее число x M , а M y на О у – y M . На координатных осях это выглядит так:

Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел ( x M , y M ) , называемую ее координатами. Абсцисса M – это x M , ордината M – это y M .

Обратное утверждение также считается верным: каждая упорядоченная пара ( x M , y M ) имеет соответствующую заданную в плоскости точку.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Определение точки М в трехмерном пространстве. Пусть имеются M x , M y , M z , являющиеся проекциями точки М на соответствующие оси О х , О у , О z . Тогда значения этих точек на осях О х , О у , О z примут значения x M , y M , z M . Изобразим это на координатных прямых.

Чтобы получить проекции точки M , необходимо добавить перпендикулярные прямые О х , О у , О z продолжить и изобразит в виде плоскостей, которые проходят через M . Таким образом, плоскости пересекутся в M x , M y , M z

Каждая точка трехмерного пространства имеет свои данные ( x M , y M , z M ) , которые имеют название координаты точки M , , x M , y M , z M – это числа, называемые абсциссой, ординатой и аппликатой заданной точки M . Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел ( x M , y M , z M ) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.

Значительное число задач стереометрии проще решать методом координат. На этом уроке учащиеся как раз таки и познакомятся с основными понятиями прямоугольной системы координат в пространстве: точка начала координат, координатная ось и координатная плоскость. А также узнают, как определяются координаты точки в пространстве.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Прямоугольная система координат в пространстве"

Вы уже знакомы с прямоугольной системой координат на плоскости, другими словами прямоугольной координатной плоскостью. Такую систему координат задают две взаимно перпендикулярные прямые, на каждой из которых выбрано направление и величина единичного отрезка. Эти прямые называют осями абсцисс и ординат.

Точку пересечения осей называют точкой начала координат.

Прямоугольную систему координат на плоскости обозначают Оху.

Каждой точке плоскости сопоставляется только одна пара чисел, которые называют её координатами. Для определения координат, из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу и ординату точки.

Определение:

Если же через точку пространства проведены три попарно перпендикулярные прямые, а на каждой из них выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.

Прямые с выбранными на них направлениями называют осями координат, а точку их пересечения — началом координат. Как и на плоскости её обычно обозначают буквой О.

Оси координат обозначают так: Ох, Оу, Оz. И называют осью абсцисс, осью ординат и, новым является название третьей оси, ось аппликат.

Прямоугольную систему координат в пространстве обозначают Охуz.

Через каждые 2 оси координат проходят координатные плоскости: Оху, Оуz и Охz. Всего таких плоскостей 3.

Каждая ось делится точкой О на два луча. В соответствии с этим, лучи, направление которых совпадает с направлением оси, называют положительными полуосями, а оставшиеся лучи — отрицательными полуосями.

Каждой точке пространства сопоставляется только одна тройка чисел, которые называют её координатами. Их определяют аналогично тому, как это делали на плоскости. Только через точку М проводят плоскости перпендикулярные координатным осям.

Точки пересечения проведённых плоскостей с осями координат назовём М₁, М₂ и М₃.

Первая координата точки М, то есть её абсцисса, равна длине отрезка ОМ₁.

Вторая координата, которую называют ординатой, равна длине отрезка ОМ₂.

Ну, а третья координата, а точнее аппликата, равна длине отрезка ОМ₃.

Координаты точки записывают в скобках, при этом первой записывают абсциссу, второй — ординату, а третьей — аппликату.

В данном случае точки М₁, М₂ и М₃ являются точками положительных полуосей, поэтому и координаты точки М будут положительными числами.

Рассмотрим примеры различного расположения точек в прямоугольной системе координат.

Задание: определить координаты точек А, В, С, D, Е и F.

После выполнения этого задания можно сделать вывод о том, что если точка лежит в некоторой координатной плоскости или на некоторой координатной оси, то её соответствующие координаты будут равны нулю.

Так если точка лежит в координатной плоскости ОИксИгрек, то её аппликата равна нулю. Если точка лежит в координатной плоскости ОИксЗэт, то её ордината равна нулю. И если точка лежит в координатной плоскости ОИгрекЗэт, то её абсцисса равна нулю.

Ну, а в случаях, когда точка лежит на одной из осей, только одна координата является ненулевой.

Задание: По координатам точек 𝐴(3;−1;0), 𝐵(0;0;−7), 𝐶(2;0;0), 𝐷(−4;0;3), 𝐸(0;−1;0), 𝐹(1;2;3), 𝐺(0;5−7), 𝐻(−√5;√3;0) определить, какие из них лежат на той или иной координатной оси или в той или иной координатной плоскости.

Решение:

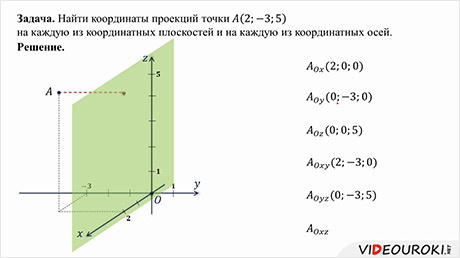
Задание: найти координаты проекций точки 𝐴(2;−3;5) на каждую из координатных плоскостей и на каждую из координатных осей.

Далее найдём координаты проекций точки А на координатные плоскости.

Проекцией точки А на координатную плоскость Оху является основание перпендикуляра, проведённого из точки А к данной координатной плоскости. При этом координаты полученной проекции будут такими же как у точки А, только аппликата станет равной нулю.

Аналогично получим проекцию точки А на координатную плоскость Оуz. Проведём перпендикуляр из данной точки к данной координатной плоскости. Его основание и является проекцией точки А на плоскость Оуz. Координаты данной проекции равны координатам точки А, только абсцисса равна нулю.

Ну, а проекция точки А на координатную плоскость Охz будет иметь координаты 2, 0, 5.

Так мы с вами нашли координаты проекций точки А на координатные оси и на координатные плоскости.

Решение: Изобразим прямоугольную систему координат. Отметим точки, являющиеся вершинами куба, координаты которых известны.

На этом уроке вы познакомились с понятием прямоугольной системы координат в пространстве. Узнали, что её задают три взаимно перпендикулярные прямые, на которых выбраны направления и единичные отрезки. Эти прямые называют координатными осями. Точку пересечения осей называют точкой начала координат.

Ось Ох называют осью абсцисс, ось Оу называют осью ординат, и новым для вас является название оси Оz — ось аппликат. Помимо осей координат в прямоугольной системе координат присутствуют и координатные плоскости: Оху, Оуz и Охz.

Всю прямоугольную систему координат в пространстве обозначают Охуz.

Любой точке пространства соответствует только одна тройка чисел х, у и z, которые и являются её координатами. Все координаты точки О начала координат равны нулю.

Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат, а их общая точка — началом координат. Она обозначается обычно буквой О.
Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz.
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.

В прямоугольной системе координат каждой точке А пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости.

Проведем через точку А три плоскости, перпендикулярные к осям координат, и обозначим через А₁, А₂ и А_3.
Точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат. Первая координата точки А (она называется абсциссой и обозначается обычно буквой х) определяется так: х = ОА₁, если А₁ точка положительной полуоси: х = - ОА₁, если А₁ точка отрицательной полуоси: х = 0, если А₁ совпадает с точкой О. Аналогично с помощью точки А₂ определяется вторая координата (ордината) y точки А, а с помощью точки А₃ третья координата (аппликата) z точки А. Координаты точки А записываются в скобках после обозначения точки: А (х; у; z), причем первой указывают абсциссу, второй ординату, третьей — аппликату.

Если точка А (х; у; z) лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю.

Читайте также:

  
• Как учить ребенка писать цифры в детском саду
  
• План обогащения развивающей среды в доу
  
• Школьный проект письмо деду морозу
  
• Как с помощью архивации можно защитить информацию кратко
  
• Что называют системой органов 6 класс биология кратко