Какие тождественные преобразования выражений вы знаете 7 класс кратко

Обновлено: 04.07.2024

Тождество — это равенство, обе части которого являются тождественно равными выражениями. Тождества делятся на буквенные и числовые.

Тождественные выражения

Два алгебраических выражения называются тождественными (или тождественно равными), если при любых численных значениях букв они имеют одинаковую численную величину. Таковы, например, выражения:

x(5 + x) и 5x + x 2 .

Оба представленных выражения, при любом значении x будут равны друг другу, поэтому их можно назвать тождественными или тождественно равными.

Так же тождественными можно назвать и числовые выражения, равные между собой. Например:

Буквенные и числовые тождества

Буквенное тождество — это равенство, которое справедливо при любых значениях входящих в него букв. Другими словами, такое равенство, у которого обе части являются тождественно равными выражениями, например:

(a + b)m = am + bm;

(a + b) 2 = a 2 + 2ab + b 2 .

Числовое тождество — это равенство, содержащее только числа, выраженные цифрами, у которого обе части имеют одинаковую численную величину. Например:

Тождественные преобразования выражений

Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, тождественное первому.

При вычислении значения выражения, раскрытии скобок, вынесении общего множителя за скобки и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения или просто преобразованием выражения. Все преобразования выражений выполняются на основе свойств действий над числами.

Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:

10x - 7x + 3x = (10 - 7 + 3)x = 6x.

Выполнение данного преобразования основано на распределительном законе умножения.

Тождественные преобразования представляют собой работу, которую мы проводим с числовыми и буквенными выражениями, а также с выражениями, которые содержат переменные. Все эти преобразования мы проводим для того, чтобы привести исходное выражение к такому виду, который будет удобен для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой теме.

Тождественное преобразование выражения. Что это такое?

Впервые встречаемся с понятием тождественных преобразованный мы на уроках алгебры в 7 классе. Тогда же мы впервые знакомимся с понятием тождественно равных выражений. Давайте разберемся с понятиями и определениями, чтобы облегчить усвоение темы.

Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Проиллюстрируем данное определение примерами.

Если мы заменим выражение x + 3 − 2 на тождественно равное ему выражение x + 1 , то мы проведем при этом тождественное преобразование выражения x + 3 − 2 .

Замена выражения 2 · a 6 на выражение a 3 – это тождественное преобразование, тогда как замена выражения x на выражение x 2 не является тождественным преобразованием, так как выражения x и x 2 не являются тождественно равными.

Обращаем ваше внимание на форму записи выражений при проведении тождественных преобразований. Обычно мы записываем исходное и полученное в ходе преобразования выражения в виде равенства. Так, запись x + 1 + 2 = x + 3 означает, что выражение x + 1 + 2 было приведено к виду x + 3 .

Последовательное выполнение действий приводит нас к цепочке равенств, которая представляет собой несколько расположенных подряд тождественных преобразований. Так, запись x + 1 + 2 = x + 3 = 3 + x мы понимаем как последовательное проведение двух преобразований: сначала выражение x + 1 + 2 привели к виду x + 3 , а его – к виду 3 + x .

Тождественные преобразования и ОДЗ

Ряд выражений, которые мы начинаем изучать в 8 классе, имеют смысл не при любых значениях переменных. Проведение тождественных преобразований в этих случаях требует от нас внимания к области допустимых значений переменных (ОДЗ). Выполнение тождественных преобразований может оставлять ОДЗ неизменной или же сужать ее.

При выполнении перехода от выражения a + ( − b ) к выражению a − b область допустимых значений переменных a и b остается прежней.

Переход от выражения x к выражению x 2 x приводит к сужению области допустимых значений переменной x от множества всех действительных чисел до множества всех действительных чисел, из которого был исключен ноль.

Тождественное преобразование выражения x 2 x выражением х приводит к расширению области допустимых значений переменной x от множества всех действительных чисел за исключением нуля до множества всех действительных чисел.

Сужение или расширение области допустимых значений переменных при проведении тождественных преобразований имеет значение при решении задач, так как может повлиять на точность проведения вычислений и привести к появлению ошибок.

Основные тождественные преобразования

Давайте теперь посмотрим, какими бывают тождественные преобразования и как они выполняются. Выделим те виды тождественных преобразований, с которыми нам приходится иметь дело чаще всего, в группу основных.

Помимо основных тождественных преобразований существует ряд преобразований, которые относятся к выражениям конкретного вида. Для дробей это приемы сокращения и приведения к новому знаменателю. Для выражений с корнями и степенями все действия, которые выполняются на базе свойств корней и степеней. Для логарифмических выражений действия, которые проводятся на основе свойств логарифмов. Для тригонометрических выражений все действия с использованием тригонометрических формул. Все эти частные преобразования подробно разбираются в отдельных темах, которые можно найти на нашем ресурсе. В связи с этим в этой стстье мы на них останавливаться не будем.

Перейдем к рассмотрению основных тождественных преобразований.

Перестановка местами слагаемых, множителей

Начнем с перестановки слагаемых местами. С этим тождественным преобразованием мы имеем дело чаще всего. И основным правилом здесь можно считать следующее утверждение: в любой сумме перестановка слагаемых местами не отражается на результате.

Основано это правило на переместительном и сочетательном свойствах сложения. Эти свойства позволяют нам переставлять слагаемые местами и получать при этом выражения, которые тождественно равны исходным. Именно поэтому перестановка слагаемых местами в сумме является тождественным преобразованием.

У нас есть сумма трех слагаемых 3 + 5 + 7 . Если мы поменяем местами слагаемые 3 и 5 , то выражение примет вид 5 + 3 + 7 . Вариантов перестановки местами слагаемых в данном случае несколько. Все они приводят к получению выражений, тождественно равных исходному.

В качестве слагаемых в сумме могут выступать не только числа, но и выражения. Их точно так же, как и числа, можно переставлять местами, не влияя на конечный результат вычислений.

В сумме трех слагаемых 1 a + b , a 2 + 2 · a + 5 + a 7 · a 3 и - 12 · a вида 1 a + b + a 2 + 2 · a + 5 + a 7 · a 3 + ( - 12 ) · a слагаемые можно переставить, например, так ( - 12 ) · a + 1 a + b + a 2 + 2 · a + 5 + a 7 · a 3 . В свою очередь можно переставить местами слагаемые в знаменателе дроби 1 a + b , при этом дробь примет вид 1 b + a . А выражение под знаком корня a 2 + 2 · a + 5 тоже является суммой, в которой можно поменять местами слагаемые.

Точно так же, как и слагаемые, в исходных выражениях можно менять местами множители и получать тождественно верные уравнения. Проведение этого действия регулируется следующим правилом:

В произведении перестановка множителей местами не влияет на результат вычислений.

Основано это правило на переместительном и сочетательном свойствах умножения, которые подтверждают верность тождественного преобразования.

Произведение 3 · 5 · 7 перестановкой множителей можно представить в одном из следующих видов: 5 · 3 · 7 , 5 · 7 · 3 , 7 · 3 · 5 , 7 · 5 · 3 или 3 · 7 · 5 .

Перестановка множителей в произведении x + 1 · x 2 - x + 1 x даст x 2 - x + 1 x · x + 1

Раскрытие скобок

Скобки могут содержать записи числовых выражений и выражений с переменными. Эти выражения могут быть преобразованы в тождественно равные выражения, в которых скобок не будет вообще или их будет меньше, чем в исходных выражениях. Этот способ преобразования выражений называют раскрытием скобок.

Проведем действия со скобками в выражении вида 3 + x − 1 x для того, чтобы получить тождественно верное выражение 3 + x − 1 x .

Выражение 3 · x - 1 + - 1 + x 1 - x можно преобразовать в тождественно равное выражение без скобок 3 · x - 3 - 1 + x 1 - x .

Группировка слагаемых, множителей

В случаях, когда мы имеем дело с тремя и большим количеством слагаемых, мы можем прибегнуть к такому виду тождественных преобразований как группировка слагаемых. Под этим способом преобразований подразумевают объединение нескольких слагаемых в группу путем их перестановки и заключения в скобки.

При проведении группировки слагаемые меняются местами таким образом, чтобы группируемые слагаемые оказались в записи выражения рядом. После этого их можно заключить в скобки.

Возьмем выражение 5 + 7 + 1 . Если мы сгруппируем первое слагаемое с третьим, то получим ( 5 + 1 ) + 7 .

Группировка множителей проводится аналогично группировке слагаемых.

В произведении 2 · 3 · 4 · 5 можно сгруппировать первый множитель с третьим, а второй – с четвертым, при этом придем к выражению ( 2 · 4 ) · ( 3 · 5 ) . А если бы мы сгруппировали первый, второй и четвертый множители, то получили бы выражение ( 2 · 3 · 5 ) · 4 .

Замена разностей суммами, частных произведениями и обратно

Замена разностей суммами стала возможна благодаря нашему знакомству с противоположными числами. Теперь вычитание из числа a числа b можно рассматривать как прибавление к числу a числа − b . Равенство a − b = a + ( − b ) можно считать справедливым и на его основе проводить замену разностей суммами.

Возьмем выражение 4 + 3 − 2 , в котором разность чисел 3 − 2 мы можем записать как сумму 3 + ( − 2 ) . Получим 4 + 3 + ( − 2 ) .

Все разности в выражении 5 + 2 · x − x 2 − 3 · x 3 − 0 , 2 можно заменить суммами как 5 + 2 · x + ( − x 2 ) + ( − 3 · x 3 ) + ( − 0 , 2 ) .

Мы можем переходить к суммам от любых разностей. Аналогично мы можем произвести обратную замену.

Замена деления на умножение на число, обратное делителю, становится возможным благодаря понятию взаимно обратных чисел. Это преобразование можно записать равенством a : b = a · ( b − 1 ) .

Это правило было положено в основу правила деления обыкновенных дробей.

Частное 1 2 : 3 5 можно заменить произведением вида 1 2 · 5 3 .

Точно также по аналогии деление может быть заменено умножением.

В случае с выражением 1 + 5 : x : ( x + 3 ) заменить деление на x можно на умножение на 1 x . Деление на x + 3 мы можем заменить умножением на 1 x + 3 . Преобразование позволяет нам получить выражение, тождественное исходному: 1 + 5 · 1 x · 1 x + 3 .

Замена умножения делением поводится по схеме a · b = a : ( b − 1 ) .

В выражении 5 · x x 2 + 1 - 3 умножение можно заменить делением как 5 : x 2 + 1 x - 3 .

Выполнение действий с числами

Выполнение действий с числами подчиняется правилу порядка выполнения действий. Сначала проводятся действия со степенями чисел и корнями из чисел. После этого мы заменяем логарифмы, тригонометрические и прочие функции на их значения. Затем выполняются действия в скобках. И затем уже можно проводить все остальные действия слева направо. Важно помнить, что умножение и деление проводят до сложения и вычитания.

Действия с числами позволяют преобразовать исходное выражение в тождественное равное ему.

Преобразуем выражение 3 · 2 3 - 1 · a + 4 · x 2 + 5 · x ,выполнив все возможные действия с числами.

Решение

Первым делом обратим внимание на степень 2 3 и корень 4 и вычислим их значения: 2 3 = 8 и 4 = 2 2 = 2 .

Подставим полученные значения в исходное выражение и получим: 3 · ( 8 - 1 ) · a + 2 · ( x 2 + 5 · x ) .

Теперь проведем действия в скобках: 8 − 1 = 7 . И перейдем к выражению 3 · 7 · a + 2 · ( x 2 + 5 · x ) .

Нам осталось выполнить умножение чисел 3 и 7 . Получаем: 21 · a + 2 · ( x 2 + 5 · x ) .

Ответ: 3 · 2 3 - 1 · a + 4 · x 2 + 5 · x = 21 · a + 2 · ( x 2 + 5 · x )

Действиям с числами могут предшествовать другие виды тождественных преобразований, таких, например, как группировка чисел или раскрытие скобок.

Возьмем выражение 3 + 2 · ( 6 : 3 ) · x · ( y 3 · 4 ) − 2 + 11 .

Решение

Первым делом проведем замену частного в скобках 6 : 3 на его значение 2 . Получим: 3 + 2 · 2 · x · ( y 3 · 4 ) − 2 + 11 .

Раскроем скобки: 3 + 2 · 2 · x · ( y 3 · 4 ) − 2 + 11 = 3 + 2 · 2 · x · y 3 · 4 − 2 + 11 .

Сгруппируем числовые множители в произведении, а также слагаемые, являющиеся числами: ( 3 − 2 + 11 ) + ( 2 · 2 · 4 ) · x · y 3 .

Выполним действия в скобках: ( 3 − 2 + 11 ) + ( 2 · 2 · 4 ) · x · y 3 = 12 + 16 · x · y 3

Ответ: 3 + 2 · ( 6 : 3 ) · x · ( y 3 · 4 ) − 2 + 11 = 12 + 16 · x · y 3

Если мы работаем с числовыми выражениями, то целью нашей работы будет нахождение значения выражения. Если же мы преобразуем выражения с переменными, то целью наших действий будет упрощение выражения.

Вынесение за скобки общего множителя

В тех случаях, когда слагаемые в выражении имеют одинаковый множитель, то мы можем вынести этот общий множитель за скобки. Для этого нам сначала необходимо представить исходное выражение как произведение общего множителя и выражения в скобках, которое состоит из исходных слагаемых без общего множителя.

В числовом выражении 2 · 7 + 2 · 3 мы можем вынести общий множитель 2 за скобки и получить тождественно верное выражение вида 2 · ( 7 + 3 ) .

Освежить в памяти правил вынесения общего множителя за скобки вы можете в соответствующем разделе нашего ресурса. В материале подробно рассмотрены правила вынесения общего множителя за скобки и приведены многочисленные примеры.

Приведение подобных слагаемых

Теперь перейдем к суммам, которые содержат подобные слагаемые. Тут возможно два варианта: суммы, содержащие одинаковые слагаемые, и суммы, слагаемые которых отличаются числовым коэффициентом. Действия с суммами, содержащими подобные слагаемые, носит название приведения подобных слагаемых. Проводится оно следующим образом: мы выносим общую буквенную часть за скобки и проводим вычисление суммы числовых коэффициентов в скобках.

Рассмотрим выражение 1 + 4 · x − 2 · x . Мы можем вынести буквенную часть x за скобки и получить выражение 1 + x · ( 4 − 2 ) . Проведем вычисление значения выражения в скобках и получим сумму вида 1 + x · 2 .

Замена чисел и выражений тождественно равными им выражениями

Числа и выражения, из которых составлено исходное выражение, можно заменять тождественно равными им выражениями. Такое преобразование исходного выражения приводит к тождественно равному ему выражению.

Рассмотрим выражение 3 + x . Здесь число 3 может быть заменено суммой 1 + 2 . Так мы получим выражение ( 1 + 2 ) + x , тождественно равное исходному.

Рассмотрим выражение 1 + a 5 , в котором степень a 5 мы можем заменить тождественно равным ей произведением, например, вида a · a 4 . Это нам даст выражение 1 + a · a 4 .

Выполненное преобразование искусственное. Оно имеет смысл лишь при подготовке к проведению других преобразований.

Рассмотрим преобразование суммы 4 · x 3 + 2 · x 2 . Здесь слагаемое 4 · x 3 мы можем представить как произведение 2 · x 2 · 2 · x . В результате исходное выражение принимает вид 2 · x 2 · 2 · x + 2 · x 2 . Теперь мы можем выделить общий множитель 2 · x 2 и вынести его за скобки: 2 · x 2 · ( 2 · x + 1 ) .

Прибавление и вычитание одного и того же числа

Прибавление и одновременное вычитание одного и того же числа или выражения являетс искусственным приемом преобразования выражений.

Рассмотрим выражение x 2 + 2 · x . Мы можем прибавить или отнять от него единицу, что позволит нам в последующем провести еще одно тождественное преобразование - выделить квадрат двучлена: x 2 + 2 · x = x 2 + 2 · x + 1 − 1 = ( x + 1 ) 2 − 1 .

Тождество — это равенство, выполняемое на всем множестве значений переменных, которые в него включены.

К примеру, тождествами являются, в том числе, квадратные выражения:

a 2 − b 2 = ( a + b ) ( a − b )

( a + b ) 2 = a 2 + 2 a b + b 2

В рассмотренных выражениях любые значения a и b обращают их в верные равенства, что полезно знать при решении примеров.

Тождественно равными выражениями называют такие два выражения, которые обладают равными значениями при всех значениях переменных.

Данное равенство существует только в том случае, когда:

Рассматриваемое равенство не является тождеством, а представляет собой уравнение. Для обозначения тождественного равенства принято использовать символ тройного равенства: ≡ .

Разница между тождеством и уравнением заключается в том, что тождество является верным при любом из значений переменных. Уравнение же верно лишь в том случае, когда имеется одно или несколько значений переменных.

Это уравнение верное только, когда ответ соответствует х = 10 .

В этом случае тождество не включает в себя переменные.

Замена чисел и выражений тождественно равными им выражениями

Тождественное преобразование выражения (преобразование выражения) представляет собой замену одних выражений на другие, которые тождественно равны между собой.

Данное объяснение преобразований позволяет значительно упростить решение задач. К примеру, для этого используют законы сокращенного умножения, арифметические свойства и другие тождества.

Рассмотрим конкретный пример:

Выполним работу по тождественным преобразованиям этой дроби:

x 3 – x x 2 – x = x ( x 2 – 1 ) x – 1 = x ( x – 1 ) ( x + 1 ) x ( x – 1 ) = x + 1

x 3 – x x 2 – x = x + 1

В результате получили тождество, которое существует, если х ≠ 0 и х ≠ 1 . То есть необходимо исключить недопустимые значения, так как знаменатель слева не должен принимать нулевые значения:

Доказательство тождеств

В процессе доказательства тождества необходимо выполнить ряд действий:

тождественно преобразовать обе или только одну часть равенства;
получить в обеих частях идентичные алгебраические выражения.

В качестве самостоятельного примера для тренировки докажем следующее тождество:

x 3 – x x 2 – x = x 2 + x x

В первую очередь избавимся от х , записав его за скобками:

x ( x 2 – 1 ) x ( x – 1 ) = x ( x + 1 ) x

Заметим, что можно сократить х :

x 2 – 1 x – 1 = x + 1

( x – 1 ) ( x + 1 ) x – 1 = x + 1

Выполним сокращение на х - 1 :

Заключим, что рассмотренное равенство является тождеством, если х ≠ 0 и х ≠ 1

Когда требуется доказать, что равенство не относится к тождеству, следует определить одно допустимое значение переменной, при котором полученные числовые выражения обращаются в неравные друг другу. К примеру:

x 2 – x x = x 2 + x x → x ≠ 0

Упростим вычисления с помощью сокращения х :

Выполним подстановку какого-то числа вместо х , например, числа 5:

Данное равенство не является тождеством.

Примеры тождеств

Изучить тождества на практике можно с помощью решения задач на различные тождественные преобразования алгебраических выражений. Ключевой целью таких действий является замена начального выражения на выражение, которое ему тождественно равно.

От перестановки местами слагаемых сумма не меняется:

От перестановки местами сомножителей произведение не меняется:

Согласно данным правилам, можно записать примеры тождественных выражений:

128 × 32 = 32 × 128

При наличии в сумме более двух слагаемых допускается группировать их путем заключения в скобки. Также можно предварительно переставлять эти слагаемые местами:

a + b + c + d = ( a + c ) + ( b + d )

Аналогичным способом группируют сомножители в произведении:

a × b × c × d = ( a × d ) × ( b × c )

Приведем примеры таких тождественных преобразований:

15 + 6 + 5 + 4 = ( 15 + 5 ) + ( 6 + 4 )

6 × 8 × 11 × 4 = ( 6 × 4 × 8 ) × 11

При увеличении или уменьшении обеих частей тождества на одинаковое число, данное тождество остается верным:

( a + b ) ± e = ( c + d ) ± e

Равенство сохраняется также при умножении или делении обеих частей этого равенства на одно и то же число:

( a + b ) × e = ( c + d ) × e

( a + b ) ÷ e = ( c + d ) ÷ e

Запишем несколько примеров:

35 + 10 = 9 + 16 + 20 ⇒ ( 35 + 10 ) + 4 = ( 9 + 16 + 20 ) + 4

42 + 14 = 7 × 8 ⇒ ( 42 + 14 ) × 12 = ( 7 × 8 ) × 12

Какую-либо разность допускается записывать, как сумму слагаемых:

Аналогичным способом можно выполнить замену частного на произведение:

Рассмотрим примеры тождественных преобразований:

76 – 15 – 29 = 76 + ( - 15 ) + ( - 29 )

42 ÷ 3 = 42 × 3 - 1

Заменить математическое выражение на более простое можно с помощью арифметических действий:

сложение;
вычитание;
умножение;
деление.

Преобразования следует выполнять с соблюдением алгоритма:

В первую очередь выполняют возведение в степень, извлекают корни, вычисляют логарифмы, тригонометрические и прочие функции.
Далее можно приступать к действиям с выражениями, заключенными в скобки.
На последнем этапе, начиная с левой стороны, двигаясь вправо, выполняют действия, которые остались. При этом умножение и деление являются приоритетными, выполняются в первую очередь. Затем можно приступить к сложению и вычитанию. Данное правило распространяется и на выражения, записанные в скобках.

14 + 6 × ( 35 – 16 × 2 ) + 11 × 3 = 14 + 18 + 33 = 65

20 ÷ 4 + 2 × ( 25 × 3 – 15 ) – 9 + 2 × 8 = 5 + 120 – 9 + 16 = 132

В арифметических выражениях можно избавляться от скобок при необходимости. Исходя из знаков в выражении, определяются правила, согласно которым раскрывают скобки.

Рассмотрим несколько примеров преобразований с помощью раскрытия скобок:

117 + ( 90 – 74 – 38 ) = 117 + 90 – 74 – 38

1040 – ( - 218 – 409 + 192 ) = 1040 + 218 + 409 – 192

22 × ( 8 + 14 ) = 22 × 8 + 22 × 14

18 ÷ ( 4 – 6 ) = 18 ÷ 4 – 18 ÷ 6

Другим распространенным действием при упрощении выражений, содержащих скобки, является вынесение за них общего множителя. В результате в скобках остаются слагаемые, поделенные на вынесенный множитель. Данный способ преобразования можно применять в выражениях, которые содержат буквенные переменные.

3 × 5 + 5 × 6 = 5 × ( 3 + 6 )

28 + 56 – 77 = 7 × ( 4 + 8 – 11 )

31 x + 50 x = x × ( 31 + 50 )

В процессе тождественных преобразований часто применяют формулы для сокращенного выражения.

Данный урок начинаем с примера, в котором заменяем некоторое выражение тождественно равным ему, но более простым. Затем сразу формулируем определение тождественного преобразования. Вспоминаем тождественные преобразования, которые нам уже знакомы (приведение подобных слагаемых, раскрытие скобок). И напоследок, выполняем несколько упражнений для закрепления материала.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Тождественные преобразования выражений"

· ввести понятия тождественного преобразования;

· повторить известные нам тождественные преобразования;

· рассмотреть примеры на тождественные преобразования.

Ранее вы уже познакомились со свойствами арифметических действий. Это переместительное свойство, сочетательное свойство и распределительное свойство.

Давайте, используя законы арифметических действий, заменим данное выражение тождественно равным ему, но более простым.

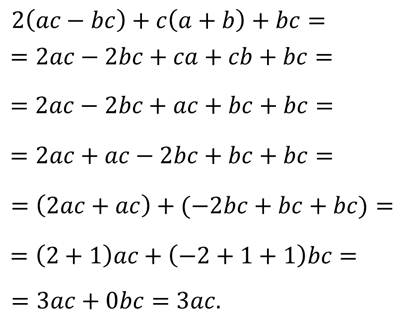
Вот таким образом мы заменили данное нам выражение тождественно равным ему, но более простым.

Сформулируем определение.

Тождественным преобразованием называется преобразование одного выражения в другое, тождественно равное ему.

Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами, о которых выше мы уже говорили.

Сейчас мы ещё вспомним некоторые тождественные преобразования, которые ранее вы уже выполняли.

А это приведение подобных слагаемых.

Итак, чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

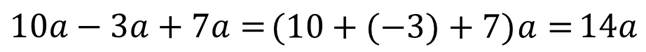
Ещё одно тождественное преобразование – раскрытие скобок.

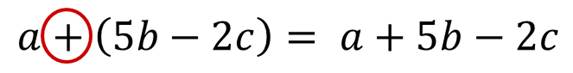
Читайте также: