Как производится умножение вектора на скаляр в физике кратко

Обновлено: 19.05.2024

1. Умножение вектора на скалярную величину. При умножении вектора на скаляр получают новый вектор " />
, длина ( модуль ) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если , или противоположно исходному вектору, если . В координатной форме, если a = (a_x;a_y;a_z) , то b = a= ;\lambda a_;\lambda a_)" />
. Следовательно, операция умножения вектора на скаляр не влияет на компланарность ( коллинеарность ) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны ( коллинеарны ), то после умножения компланарность ( коллинеарность ) между ними сохранится.

Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е. =|\overrightarrow|\cdot\overrightarrow_b=b\cdot\overrightarrow_b" />
1 Модуль вектора можно обозначать |\overrightarrow| или просто b. Из последнего равенства следует, что _b=\frac<\overrightarrow>" />
. Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности: , а также свойством дистрибутивности: )\cdot\alpha=\overrightarrow\cdot\alpha+\overrightarrow\cdot\alpha" />
.

2. Скалярное произведение векторов.

Определение 14. Скалярным произведением двух векторов и " />
называется число S , равное |\cos(\overrightarrow^\overrightarrow)" />
. Эта операция обозначается " />
или )." />

В частности, скалярный квадрат вектора равен квадрату его длины, т.е.

$(\overrightarrow)^2=\overrightarrow\cdot\overrightarrow=|\overrightarrow|\cdot|\overrightarrow|\cdot\cos(\overrightarrow^<\wedge> \overrightarrow)=a\cdot a=a^2 .$

Если один из перемножаемых векторов единичный, то:

$\overrightarrow\cdot\overrightarrow =a\cdot\cos(\overrightarrow^\overrightarrow)=\text_<\overrightarrow>\overrightarrow=\overrightarrow_<\overrightarrow>$

В этом случае результат представляет собой проекцию вектора на направление единичного вектора " />
. Следовательно, любой вектор можно представить как +a_y\cdot\overrightarrow+a_z\cdot\overrightarrow" />
, где a_x,a_y,a_z - проекции вектора соответственно на оси 0х, 0у и 0z .

Если вектор представлен через проекции на базисные векторы , то говорят о разложении вектора по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора на эти оси. Из этого же рисунка следует, что модуль вектора численно будет равен " />
.

Из определения скалярного произведения следует, что любой вектор , независимо от типа, можно представить в виде:

$\overrightarrow=(\overrightarrow\cdot\overrightarrow )\overrightarrow+(\overrightarrow\cdot\overrightarrow)\overrightarrow+(\overrightarrow\cdot\overrightarrow)\overrightarrow,$

где )" />
, )" />
и " />
есть скалярное произведение вектора с ортами осей координат. Тогда из последнего равенства имеем

где , и - углы, которые составляет вектор соответственно с осями 0х, 0у и 0z .

Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е. =\overrightarrow\cdot\overrightarrow" />
и )\cdot\overrightarrow=\overrightarrow\cdot\overrightarrow+\overrightarrow\cdot\overrightarrow" />
. Можно убедиться самостоятельно в том, что всегда выполняется равенство

$(\overrightarrow\cdot\overrightarrow )\alpha=\overrightarrow\cdot(\overrightarrow\alpha)=(\overrightarrow\alpha)\cdot\overrightarrow.$

Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда

$\cos(\overrightarrow^ \overrightarrow)=0,\;\text (\overrightarrow^\overrightarrow)=\frac<\pi>.$

Замечание 2. \cdot\overrightarrow=\overrightarrow\cdot\overrightarrow=\overrightarrow\cdot\overrightarrow=0" />
, где , \overrightarrow,\overrightarrow" />
- единичные векторы (орты) осей координат 2 При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).

$\overrightarrow Замечание 3. \cdot\overrightarrow=\overrightarrow\cdot\overrightarrow=\overrightarrow\cdot\overrightarrow=1$
.

Замечание 4. Скалярное произведение векторов в координатной форме

$\begin \overrightarrow\cdot\overrightarrow=(a_x\overrightarrow+a_y\overrightarrow+a_z\overrightarrow)\cdot(b_x\overrightarrow+b_y\overrightarrow+b_z\overrightarrow)= \\ =a_x b_x (\overrightarrow)^2+a_y b_y (\overrightarrow)^2+a_z b_z(\overrightarrow)^2=a_x b_x+a_y b_y+a_z b_z. \end$

Замечание 5. Используя формулу скалярного произведения векторов и " />
, можно найти выражение косинуса угла между этими векторами через их проекции на орты:

$\cos(\overrightarrow^<\wedge> \overrightarrow)=\frac<\overrightarrow\cdot\overrightarrow><|\overrightarrow|\cdot|\overrightarrow|>=\frac\cdot\sqrt>.$

Если , то это значит, что угол между векторами больше 90 , т.е. тупой, а если , то угол острый.

Замечание 6. Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS .

Естественно считать, что умножение вектора а на целое положительное число сводится к последовательному сложению вектора а с самим собою раз (рис. 18).

В результате получается новый вектор , имеющий то же направление, что и данный вектор а, и в раз больший модуль:

Умножение вектора а на отрицательное число естественно считать равносильным умножению противо

положного вектора -а на абсолютную величипу этого числа;

т. е. считать, что при таком умножении получается вектор, противоположно направленный по отношению к а (рис. 19).

Обобщение этих определений приводит к следующему общему определению.

Определение. Произведением вектора и скаляра называется новый вектор, который имеет:

1) модуль, равный произведению модуля умножаемого вектора на абсолютную величину скаляра;

2) направление, одинаковое с умножаемым вектором, если скаляр положительный, и противоположное, если скаляр отрицательный.

Произведение вектора а и скаляра X обозначается или Таким образом,

Замечание. Из определения следует, что произведение равно нулю тогда и только тогда, когда один из множителей равен нулю:

Найдем сумму двух векторов $\vec a$ (рис. 1, а). Получился вектор $\vec c = \vec a+\vec a$, направленный так же, как и вектор $\vec a$, и модуль которого равен $2a \,$, т.е. $\vec c = 2\vec a$ (рис. 1, б). Если сложить k векторов $\vec a$, то получится вектор $\vec c = \underbrace _$, направленный в ту же сторону, что и вектор $\vec a$, и имеющий модуль $k \cdot a$, т.е. $\vec c = k \cdot \vec a$.

Рассмотрим вектор $\vec b = -1 \cdot \vec a$. Вектор $\vec b$ будет направлен в сторону, противоположную вектору $\vec a$, а модуль его будет равен а (рис. 2, а).

Если сложить k векторов $\vec b$, то получится вектор $\vec d = \underbrace _$, направленный в ту же сторону, что и вектор $\vec b$, и модуль которого равен $k \cdot b$, т.е. $\vec d = k \cdot \vec b$ (рис. 2, б).

a б в Рис. 2.

Так как $\vec b = -\vec a$ , то $\vec d = -k \cdot \vec a$ (рис. 2, в). Из рисунка видно, что вектор $\vec d$ направлен в сторону, противоположную направлению вектора $\vec a$, и модуль его равен $k \cdot a$.

Обобщая выше сказанное, можно сделать вывод, что

при умножении вектора $\vec a$ на скаляр k получаем вектор $\vec c = k \cdot \vec a$, модуль которого равен $k \cdot a$, и направленный

в ту же сторону, что и вектор $\vec a$, если скаляр $k > 0\,$;

Различают скалярное и векторное произведение векторов.

1. При скалярном умножении векторов $\vec a$ и $\vec b$ получается такой скаляр с, что $c = a \cdot b \cdot \cos \alpha$, где $\alpha\,$ – угол между векторами $\vec a$ и $\vec b$.

Применяются следующие способы обозначения скалярного произведения\[\vec a \cdot \vec b\] или $\left ( \vec a , \vec b \right )$.

2. При векторном произведении векторов $\vec a$ и $\vec b$ получается такой вектор $\vec c$, что его модуль равен $c = a \cdot b \cdot \sin \alpha$, где $\alpha\,$ – угол между векторами $\vec a$ и $\vec b$.

Применяются следующие способы обозначения векторного произведения\[\vec a \times \vec b\] или $\left [ \vec a , \vec b \right ]$.

Направлен вектор $\vec c$ так, что он перпендикулярен плоскости, в которой лежат вектора $\vec a$ и $\vec b$, и совпадает с поступательным движением правого винта (правой руки) при его повороте от $\vec a$ к $\vec b$ на угол меньший $\pi\,$ (рис. 6).

В старших классах на уроках алгебры, геометрии и физики ученики решают задачи с числами-скалярами. Для нахождения результата используется формула скалярного произведения векторов: (а, а) > 0, для всех а≠0. Полученное значение не зависит от системы координат. Оно характеризует длину сомножителей и угол, образованный между ними. Подобной операции соответствует линейность.

Трактовка понятий

Под скалярным произведением (СП) в пространстве над полем вещественных чисел подразумевается функция (x, y) для соответствующих элементов, принадлежащих указанному координатному пространству. Из определения вытекает линейность СП по первичному аргументу.

Для косинуса и синуса справедливо смешанное сопряжение. СП принимает положительную определённость, если соблюдается условие, что x=0. Для вычислений показателя в алгебре используется следующая форма: а = [a1, a2, …, an] и b = [b1, b2, …, bn].

Пример: нужно найти в трёхмерном пространстве произведение двух скаляров [1, 3, −5] и [4, −2, −1]. Решение: необходимо перемножить градиенты (вектора). [1, 3, −5] х [4, −2, −1] = 1 х 4 + 3 х (-2) + (-5) х (-1) = 3.

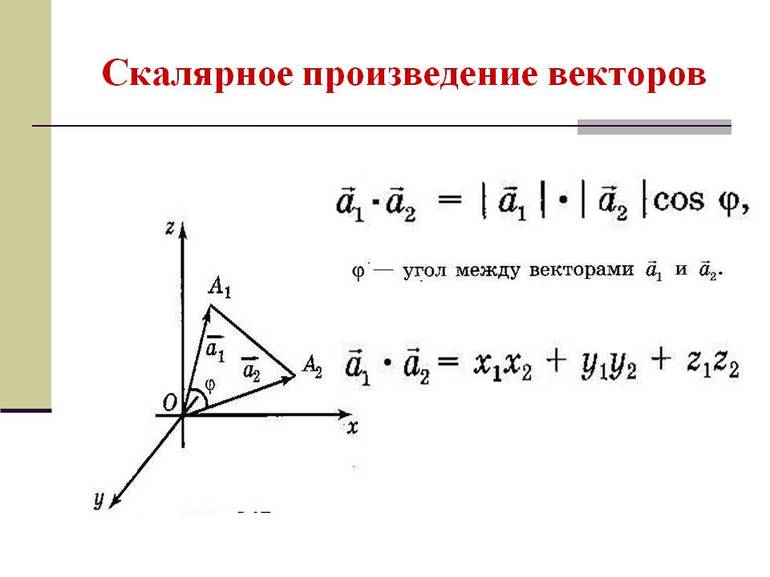
Геометрическое определение отличается от физического и алгебраического. Чтобы вычислить СП, используя длину и угол между градиентами, которые введены независимым способом, используется следующее выражение: (а, b) = lal x lbl x cos (a, b). Базисом аксиоматики считается скалярное произведение. После его нахождения определяется длина основного вектора и угла.

Сам угол является числом. Чтобы дать ему значение, вычисляется гиперболический косинус: отношение модуля СП к произведению длин векторов. При перпендикулярности либо ортогональности на плоскости СП равняется нулю. Это свойство скалярного произведения векторов характерно для любого промежутка с положительно определённым СП.

При соблюдении такого условия пространство называется вещественным либо комплексным. Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).

Если скалярное произведение отрицательное либо не считается знакоопределённым, промежуток называется индефинитной метрикой. Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:

Описание свойств

С помощью специальных математических онлайн сервисов или калькулятора легко находится значение СП через теорему косинусов: a = arccos (a, b)/√(а, а)(b, b). Знак зависит от косинуса угла. В норме значения векторов только положительные. СП больше нуля, если угол острый, и меньше, когда он тупой.

Главные свойства умножения скаляров:

Если умножить СП само на себя, получится значение, равное либо большее нуля.

СП, умноженное само на себя, равно нулю, если скаляр равен нулевому вектору.

СП скаляра самого на себя равняется квадрату его модуля.

Для скалярного умножения характерна коммуникативность.

Если СП двух отличных от нуля векторов равно 0, тогда множители считаются ортогональными.

Для операции скалярного умножения характерна дистрибутивность (согласованные бинарные операции, определённые на одном множестве).

Задача 1: вычислить СП векторов а = и b = . Решение: а х b = 1 х 4 + 2 х 8 = 20.

Задача 2: найти СП скаляров а и b, если из длины равны 3 и 6, а угол — 60 градусов. Решение: а х b = lal x lbl cos α = 3 х 6 х cos60 = 9. Для лучшего усвоения материала два вектора перемножается с помощью матрицы. Чтобы различать множители, первый оформляется в строку, а второй — в столбец. Если в условиях задачи указываются три величины, тогда последняя оформляется в скобки в форме квадратов. Их скалярное произведение вычисляется путём умножения матриц. Результат — единственное число.

Задача 3: нужно найти СП пар векторов: а = (1; 5; 1), b = (1; -5; 2) и с = (2; 1; 3/2), d = (0; 0; 1). Решение: вычисления проводятся с помощью матричного представления. Первый вектор записывается в строку, а второй — в столбец. Чтобы найти скалярное произведение векторов, потребуется умножить матрицу-строку на матрицу-столбец. Если вектор а умножить на вектор b, получится -22. Аналогично находится значение второй пары. Результат равен 3/2. Простым обобщением конечномерного СП в тензорной (линейной) алгебре считается свёртка с повторяющимся индексом.

Применение в физике

Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.

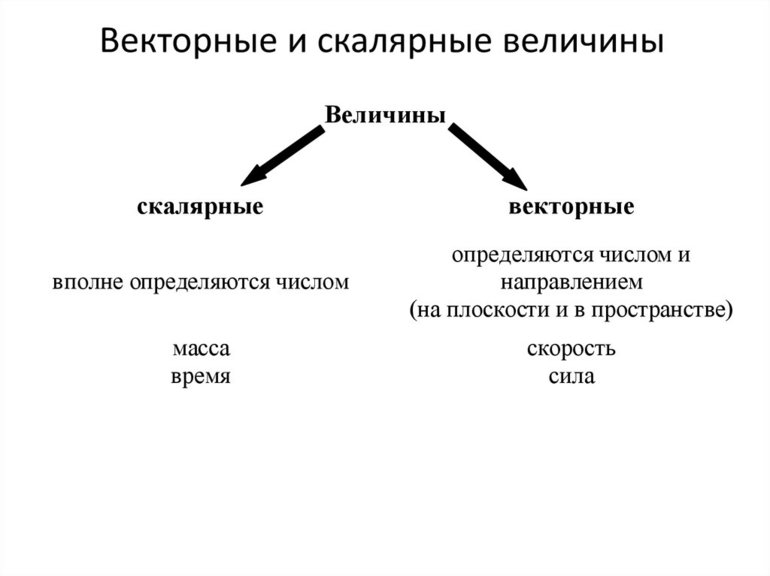
Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:

масса тела, равная 4 кг;

температура воздуха на уровне +10 градусов.

В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.

Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.

Если рассматривать векторную физическую величину, она характеризуется следующим образом:

Неотрицательность.

Направленность в пространстве.

Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной. В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.

Если на земле лежит кирпич массой в 1 кг и на него действует сила в 100 Н (модуль), потребуется найти направление движения объекта. Невозможно выяснить параметр, если нет информации о направлении действия силы. Если она идёт вверх, тогда и кирпич будет двигаться в аналогичном направлении.

Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.

Для обозначения вектора в физике используются латинские буквы и стрелка:

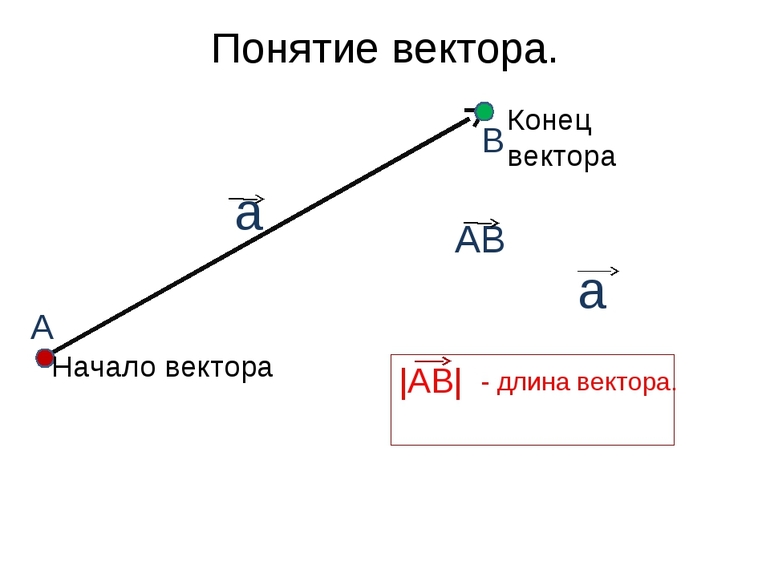
Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.

Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.

Читайте также:


Докажите что организм человека функционирует как единое целое кратко

Eine alte deutsche stadt was gibt es hier план урока

Что такое штатгальтер в нидерландах кратко

Какими современными методами можно определить возраст предковых форм человека кратко

Почему андрей боголюбский всегда ходил с высоко поднятой головой биология 8 класс кратко