Генеральная совокупность и выборка дискретные и интервальные вариационные ряды план урока

Обновлено: 05.07.2024

Статистической совокупностью называется совокупность объектов, одинаковых в каком-либо отношении, но в то же время обладающих варьирующими (изменчивыми) признаками. Вся исследуемая совокупность однородных объектов называется генеральной совокупностью.Множество из объектов, отобранных случайным образом из генеральной совокупности, называетсявыборочной совокупностью или выборкой.Число объектов, попавших в выборку, называется объемом выборки.Метод основанный на том, что по данным обследования выборки, взятой из генеральной совокупности, делается заключение о всей генеральной совокупности, называется выборочным методом.Выборка называется репрезентативной, если каждый элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.Если из генеральной совокупности отобрана выборка объема n, то количественное значение признака в этой выборке - это случайная величина, возможные значения которой обозначают символами X₁, X₂,…,X_k и называютвариантами.Числа n_i объектов с одинаковыми значениями вариант называются частотами (весами) и обозначаются n_i,n₂,…,n_k.

Вариационный ряд.

Последовательность значений вариант, расположенных в возрастающем порядке, называетсявариационным рядом.Статистическим распределением называют вариационный ряд значений выборки и соответствующих им частот n_i или относительных частот W_i.

X_i	X₁	X₂	…	X_k
n_i	n₁	n₂	…	n_k

Полигон и гистограмма.

Полигоном частот(относительных частот) называется ломаная линия с вершинами в точках (x_k , n_k), где x_k – варианта, n_k – ее частота, или (x_k , W_k), где W_k - относительная частота.Для непрерывных распределений более наглядное представление о характере распределения случайной величины дает гистограмма.Гистограммойчастот называется ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотой n_i/h, где h - длина каждого частичного интервала.Если соединить середины верхних прямоугольников гистограммы, то получим полигон частот.

Числовые характеристики выборки.

Для изучения основных свойств статистического распределения используют выборочные числовые характеристики. Для нахождения центра распределения вычисляют различные типы средних величин, моду и медиану, степени вариации-размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации и другие величины.

1. Выборочная средняя арифметическая:

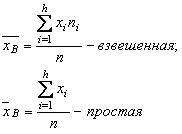
(1)

2. Выборочная средняя квадратическая:

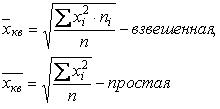
(2)

3. Выборочная средняя геометрическая:

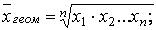
(3)

При вычислении различных типов средних величин для одного и того же вариационного ряда всегда имеем

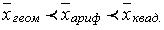
Эти неравенства характеризуют свойство мажорантности средних.

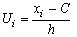
Для упрощения вычисления выборочной средней арифметической удобно переходить от данных вариант X_i к условным вариантам , где h - разность между соседними вариантами, C - ложный нуль (варианта с наибольшей частотой):

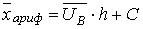
(4)

4. Модой М₀ называется варианта, имеющая наибольшую частоту.

5. Медианой М_е называется такая варианта, которая делит вариационный ряд распределения на две равные части, т.е. варианта, находящаяся в середине ряда распределения.Если в дискретном вариационном ряду (2k+1) значений, то M_e = x_k+1.

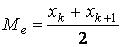
Если число вариант четное n = 2k, то медиана определяется как среднее арифметическое из двух серединных значений, т.е. .

6. Размах вариации R определяется как разность между максимальным и минимальным вариантами, т.е.

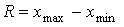
. (5)

7. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений вариант от средней арифметической

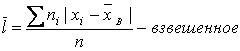
(6)

8. Дисперсиейназывается средний квадрат отклонения всех значений признака от его средней величины.

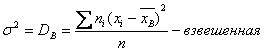
(7)

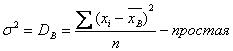
Исправленная дисперсия

(8)

10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:

(9)

Среднее квадратическое отклонение называют также стандартным отклонением.

11. Коэффициент вариацииV - это выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

(10)

Timeweb - компания, которая размещает проекты клиентов в Интернете, регистрирует адреса сайтов и предоставляет аренду виртуальных и физических серверов. Разместите свой сайт в Сети - расскажите миру о себе!

Виртуальный хостинг

Быстрая загрузка вашего сайта, бесплатное доменное имя, SSL-сертификат и почта. Первоклассная круглосуточная поддержка.

Производительность и масштабируемые ресурсы для вашего проекта. Персональный сервер по цене виртуального хостинга.

Выделенные серверы

При изучении реальных явлений часто бывает невозможно обследовать все элементы совокупности. Вместо изучения всех элементов совокупности, которую называют генеральной совокупностью , обследуют ее значительную часть, выбранную случайным образом, называемую выборкой . Выборку называют репрезентативной , если в ней присутствуют все значения случайной величины примерно в тех же пропорциях, что и в генеральной совокупности.

- объем генеральной совокупности - объем репрезентативной выборки - частоты - частоты в генеральной совокупности

Для идеально составленной репрезентативной выборки должно выполняться равенство: Где i – порядковый номер значения признака (1 ≤ i ≤ k) .

Пример 1 Фабрика резиновых изделий выиграла тендер на изготовление армейских противогазов. Для определения того, сколько противогазов каждого из пяти существующих размеров следует изготовить, были сделаны замеры у N =100 случайным образом выбранных солдат ближайшей воинской части. Распределение размеров противогазов X по частотам M оказалось следующим: X 0 1 2 3 4 M 5 21 47 22 5 Сколько противогазов каждого размера будет изготавливать фабрика?

N=100 солдат (объем репрезентативной выборки) - объем генеральной совокупности Количество противогазов соответствующего размера можно найти по формуле (2). Размер ( X) 0 1 2 3 4 Частота в выборке (М) 5 21 47 22 5 Относительная частота Количество противогазов

Размах и центральные тенденции

1. Размах, мода и медиана Имеются: 1) распределение случайной величины X — числа прочитанных за каникулы книг десятью девочками по частотам М; 2) распределение по частотам случайной величины У — числа прочитанных за каникулы книг девятью мальчиками того же класса. X 3 4 5 8 12 M 3 2 3 1 1 Y 3 4 5 6 7 M 2 4 1 1 1

Нужно сравнить интерес к чтению девочек и мальчиков этого класса. Для сравнения предложенных совокупностей могут быть использованы различные характеристики. Перечислим некоторые из них. Выпишем последовательность: 3, 3, 3, 4, 4, 5, 5, 5, 8, 12 3, 3, 4, 4, 4, 4, 5, 6, 7.

Размах (обозначается R) — разница между наибольшим и наименьшим значениями случайной величины. Мода (обозначим Мо) — наиболее часто встречающееся значение случайной величины. Медиана (обозначим Me) — это так называемое серединное значение упорядоченного ряда значений случайной величины.

Пример 1. Вычислить размах, моду и медиану для последовательности: -2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1.

Средним значением случайной величины X (обозначается ) называют среднее арифметическое всех её значений. Если все значения случайной величины X 1 , Х 2 ,…,Х N различны, то 2. Среднее значение

Если значения случайной величины X l , Х 2 . X k имеют в совокупности соответственно частоты М 1 ,М 2 , …, М k , то Зная, что , формулу (4) можно переписать в виде

Подчёркнем, что существует возможность измерить, охарактеризовать совокупность одним числом , к которому стремятся все её значения. Не для каждой совокупности имеет смысл формально находить центральные тенденции . Мода Медиана Среднее значение Меры центральной тенденции

По теме: методические разработки, презентации и конспекты

Создание запросов на выборку в базах данных

Цели практического занятия – познакомить учащихся с понятиями "запрос в БД", “запрос на выборку”, а также показать практическое применение запросов и научить создавать запросы на выборку информации в .

теория вероятности выборка.

Формирование простых запросов на выборку в базах данных

Конспект урока на тему "Формирование простых запросов на выборку в базах данных".

Итоговая контрольная работа по геометрии для учащихся 11 класса (выборка из ЕГЭ)

Предлагаемая (примерная) контрольная работа по геометрии для учащихся 11 класса поможет учителю проверить уровень знаний и умений учащихся по всему материалу стереометрических заданий, входящих в сост.

Выборка заданий "Обособление определений" с ФИПИ. 2018

Задания, связанные с поиском предложений, содержащих обособленное определение.

Методическая разработка. Самостоятельная работа по теме "Нахождение математического ожидания и дисперсии дискретной случайной величины. Находить моду, медиану, среднее арифметическое выборки, размах выборки"

Самостоятельная работа проводится на 2 курсе в СПО по математике. Предлагается справочный материал по данной теме,разбираются примеры. Студентам предлагается ряд задач решить самостоятельно. В конце р.

Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. Понятие о задачах математической статистики.

Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. Понятие о задачах математической статистики.

Презентация на тему: " Основы математической статистики Лекция 19. План лекции: 1.Задачи математической статистики. 2.Дискретные и интервальные ряды распределения. Числовые." — Транскрипт:

1 Основы математической статистики Лекция 19

2 План лекции: 1.Задачи математической статистики. 2.Дискретные и интервальные ряды распределения. Числовые характеристики. 3.Точечные и интервальные оценки.

3 Что такое математическая статистика? математическая статистика – это одновременно искусство и наука извлечения полезной информации из данных, полученных в результате наблюдений или экспериментов

4 Объекты, изучаемые математической статистикой Генеральная совокупность – конечное или бесконечное множество объектов, обладающих определенными математическими свойствами. Выборка - некоторое число случайным образом выбранных объектов из конечной или бесконечной генеральной совокупности; число выбранных объектов называют объемом выборки.

5 Какие задачи нас интересуют? - определение закона распределения случайной величины по выборочным данным; - задача проверки правдоподобия гипотез (отличия характеристик выборки от некоторых неслучайных величин; отличия характеристик нескольких выборок; связь случайных величин из разных выборок); - Задача нахождения неизвестных параметров распределения.

6 Статистическая функция распределения Пусть имеется некоторая случайная величина Х, закон распределения которой неизвестен и требуется проверить гипотезу о том, что эта случайная величина подчиняется тому или иному закону. С этой целью над случайной величиной проводится ряд независимых опытов. В каждом из них случайная величина Х принимает определенное значение. Первичный статистический материал: совокупность найденных значений Х (простой статистический ряд). Эти данные необходимо обрабатывать, но как?

7 Статистическая функция распределения случайной величины Х Рассмотрим эксперимент, который поможет понять смысл этой функции: Дана некоторая группа людей, мы измеряем их рост и пытаемся определить закономерности распределения людей по росту.

8 Результаты эксперимента Эмпирическая функция распределения Эмпирическая функция плотности распределения

9 Математическая статистика (числовые данные) Статистика случайных величин (одномерная статистика ) Многомерная статистика (факторный анализ) Временные ряды

10 Задачи одномерной статистики Описательная статистика (представление экспериментальных данных, определение точечных и интервальных оценок) Проверка статистических гипотез (о законе распределения, параметрах распределения)

11 Значения изучаемого признака называются вариантами Последовательность вариант, расположенных в возрастающем порядке называется вариационным рядом Например: 172, 179, 158, 186, 164 Вариационный ряд: 158, 164, 172, 179, 186

12 Непараметрические характеристики Me-медиана Варианта, которая делит ряд пополам 158, 164, 172, 175, 175, 179, 186 при n- нечетном Ме= , 164, 168, 172, 174, 175, 179, 186 при n- четном

13 Непараметрические характеристики Mo-наиболее часто встречающаяся варианта 158, 164, 172, 175, 175, 175, 179, 186 Мо= , 164, 173, 173, 175, 175, 179, 186 бимодальные выборки- если два несмежных значения имеют одинаковые частоты

14 Вариационные ряды дискретныенепрерывные Статистическим рядом распределения называется набор вариант и соответствующих им абсолютных и относительных частот

15 Статистический ряд распределения ХX1X1 X2X2 …XnXn mm1m1 m2m2 …mnmn m/nm 1 /nm 2 /n…m n /n

16 Да Нет М σ, М m, M (95% ДИ) Сравнение 2-х выборок по критерию Стьюдента Корреляция по Пирсону Параметрическая статистика Ме [25%-75%], Мo, Min-Max Сравнение 2-х выборок по критериям Манна- Уитни, Вилкоксона Корреляция по Спирмену Непараметрическая статистика

17 Основные этапы исследования: Сгруппировать исследуемый ряд по классам. Подсчитать середины интервалов и частоты попадания в интервал. Построить гистограмму и полигон распределения. Найти эмпирическую функцию распределения и построить ее график. Вычислить числовые (точечные) характеристики распределения. Проверить гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону, используя критерии асимметрии и эксцесса. Проверить гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону, используя критерий Пирсона 2

18 Ряд распределения студентов по росту

19 Размах распределения Из имеющихся значений признака Х выбирают наименьшее (Хmin), наибольшее (Хmax), определяют размах распределения (Хmax – Хmin) =39

20 X m m/n4/50 0,08 14/50 0,28 20/50 0,4 9/50 0,18 3/50 0,06 0,08/10 0,0080,0280,040,0180,006 Статистический ряд распределения студентов по росту

21 Гистограмма распределения студентов по росту (m, m/n, f(x))

22 Функция распределения вероятностей X

25 Интервал mip=mi/n *p ( - M) 2 ( - M) 2 * p ,0811,6345,9627, ,2843,473,9620, ,4661,960, ,1831,5129,9623, ,0611,1457,9627, ,6100,04 Числовые характеристики

27 Числовые характеристики статистического распределения Среднее Свойства точечных оценок: дисперсия Оценка называется несмещённой, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности Оценка называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности

28 Доверительный интервал для роста студентов с вероятностью p=0,95 ( =0,05); M(x)=163,6 см, σ=10 см Δх=1, см Следовательно, рост студентов находится в интервале: 163,6-20

Читайте также: