Что такое рациональное число кратко

Обновлено: 06.07.2024

Все слышали о рациональных числах, но не все понимаю, что они из себя представляют. На самом деле все просто.

Рациональное число – это результат деления двух целых чисел. Например, число 2 – результат деления 4 и 2, а число 0,2 – это 2 поделенное на 10. Любое рациональное число мы можем представить для себя в виде дроби m/n , где m является целым числом, n – натуральным числом.

Как выглядят рациональные числа? Это могут быть:

Дроби (1/2, 5/10)
Целые числа (1, 2, 5)
Смешанные числа
Десятичные дроби (0,14, 4,1)
Бесконечные периодические дроби (например, при делении 10 на 3, мы получим 3,33333…)

Q – обозначение множества рациональных чисел.

Свойства рациональных чисел

Каждое натуральное число является рациональным.
Каждое целое число является рациональным.
Рациональные числа следуют правилу сочетательного и переместительного свойства. То есть от перемены мест слагаемых значение суммы не измениться.

2+3=5 и 3+2=5, значит 2+3=3+2.

14+(1+4)=19 и (14+1)+4=19, значит 14+(1+4)=(14+1)+4

a × b = b × a

a × (b × c) = (a × b) × c

а × 1 = а

а × 1/a = 1

а × 0 = 0

а × b = 0

3х4=12 и 4х3=12, значит 3х4=4х3

5х(2х3)=30 и (5х2)х3=30, значит 5х(2х3)= (5х2)х3

Для рациональных чисел будет справедлив и распределительный закон умножения.

(а + b) × с = ас + bс

(а – b) × с = ас – bс

Иррациональные числа и корни

Для того, чтобы лучше понять что из себя представляют рациональные числа, следует знать какие числа ими не являются. А точнее, какие числа будут иррациональными. Такие числа невозможно записать в виде простой дроби:

Число ПИ, которое равно примерно 3,14. Его можно представить в виде дроби, но это значение будет только примерное.
Некоторые корни. Например, корень из 2 или из 99 нельзя записать в виде дроби
Золотое сечение, которое примерно равно 1,61. Тут ситуация обстоит так же, как и с числом ПИ.
Число Эйлера, которое приблизительно равно 2,718, тоже не является рациональным.

Большинство иррациональных чисел встречается среди корней, но далеко не все корни иррациональные. Например, корнем из числа 4 является число 2, а его можно представить в виде дроби. То есть корень из числа 4 – рациональное число.

Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:

Данная статья посвящена изучению темы "Рациональные числа". Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа - числа, которые можно представить в виде положительной обыкновенной дроби a b , отрицательной обыкновенной дроби - a b или числа ноль.

Таким образом, можно оставить ряд свойств рациональных чисел:

Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число n можно представить в виде дроби 1 n .
Любое целое число, включая число 0 , является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, 15 = 15 1 , - 352 = - 352 1 .
Любая положительная или отрицательная обыкновенная дробь a b является рациональным числом. Это следует напрямую из данного выше определения.
Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.
Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом.
Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа 5 , 105 , 358 , 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа - 2 , - 358 , - 936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби 3 5 , 8 7 , - 35 8 также являются примерами рациональных чисел.

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа - это такие числа, которые можно представить в виде дроби ± z n , где z - целое число, n - натуральное число.

Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:

0 n = 0 ÷ n = 0 ; - m n = ( - m ) ÷ n = - m n .

Таким образом, можно записать:

z n = z n , п р и z > 0 0 , п р и z = 0 - z n , п р и z 0

Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа - 3 , 0 , 5 , - 7 55 , 0 , 0125 и - 1 3 5 . Все эти числа являются рациональными, так как их можно записать в виде дроби с целым числителем и натуральным знаменателем: - 3 1 , 0 1 , - 7 55 , 125 10000 , 8 5 .

Приведем еще одну эквивалентную форму определения рациональных чисел.

Определение 3. Рациональные числа

Рациональное число - это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.

Данное определение напрямую следует из самого первого определения этого пункта.

Подведем итог и сформулируем резюме по данному пункту:

Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.
Каждое рациональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель - натуральным числом.
Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.

Какое из чисел является рациональным?

Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.

Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос "рационально ли число?" является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.

Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения - рациональное число.

Например, значение выражения 2 · 3 1 8 - 0 , 25 0 , ( 3 ) является рациональным числом и равно 18 .

Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.

Теперь разберемся со знаком корня.

Оказывается, что число m n , заданное в видя корня степени n от числа m рационально лишь тогда, когда m является n -ой степенью какого-то натурального числа.

Обратимся к примеру. Число 2 не является рациональным. Тогда как 9 , 81 - рациональные числа. 9 и 81 - полные квадраты чисел 3 и 9 соответственно. Числа 199 , 28 , 15 1 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел.

Теперь возьмем более сложный случай. Является ли рациональным число 243 5 ? Если возвести 3 в пятую степень, получается 243 , поэтому исходное выражение можно переписать так: 243 5 = 3 5 5 = 3 . Следовательно, данное число рационально. Теперь возьмем число 121 5 . Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст 121 .

Для того, чтобы узнать, является ли логарифм какого-то числа a по основанию b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число log 2 5 . Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби log 2 5 = m n .По свойствам логарифма и свойствам степени справедливы следующие равенства:

5 = 2 log 2 5 = 2 m n 5 n = 2 m

Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log 2 5 не является рациональным числом.

Стоит отметить, что при определении рациональности и иррациональности чисел не стоит принимать скоропостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом. Наглядный пример: 2 · 2 = 2 .

Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида 2 log 2 3 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: 2 log 2 3 = 3 .

О чем эта статья:

6 класс, 8 класс

Определение рациональных чисел

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.

Рациональные числа — это те, которые можно представить в виде

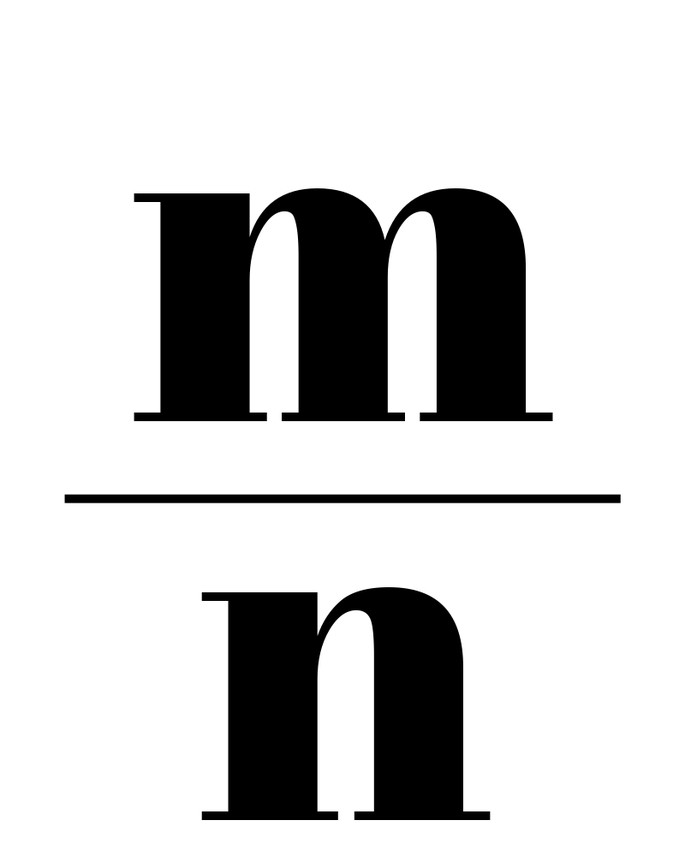
где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

десятичная дробь 1,15 — это 115/100;
десятичная дробь 0,5 — это 1/2;
целое число 0 — это 0/1;
целое число 6 — это 6/1;
целое число 1 — это 1/1;
бесконечная периодическая дробь 0,33333. — это 1/3;
смешанное число — это 25/10;
отрицательная десятичная дробь -3,16 — это -316/100.

Свойства рациональных чисел

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Переместительное свойство сложения: a + b = b + a.
Сочетательное свойство сложения: (a + b) +c = a + (b + c).
Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a.
У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0.
Переместительное свойство умножения: ab = ba.
Сочетательное свойство умножения: (a * b) * c = a * (b * c).
Произведение рационального числа и едины не изменяет это число: a * 1 = a.
У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1.
Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Кроме основных перечисленных есть еще ряд свойств:

Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).

Распределительный закон позволяет переписать выражение:

a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).

Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a - b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Определение иррационального числа

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби

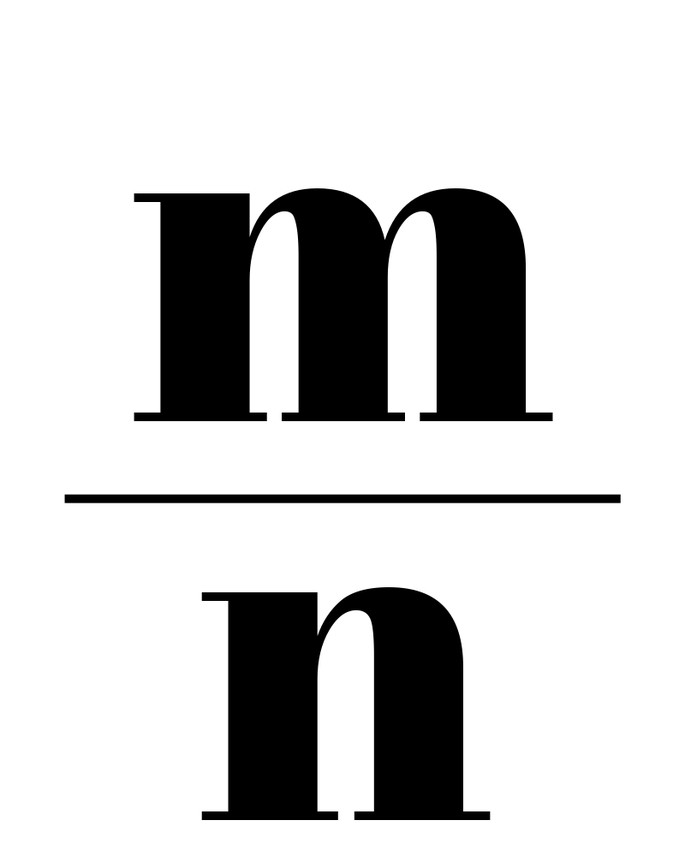
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

π = 3,1415926.
√2 = 1,41421356.
e = 2,71828182…
√8 = 2.828427.
-√11= -3.31662…

Обозначение множества иррациональных чисел: латинская буква I.

Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел:

результат суммы иррационального числа и рационального равен иррациональному числу;
результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Различие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.

А вот, что точно не является натуральным числом:

Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
Отрицательные числа: -1, -2, -3, -4.
Дроби: 1/2, 3/4, 5/6.

Целые числа — это натуральные числа, противоположные им и нуль.

Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.

Рациональные числа — это конечные дроби и бесконечные периодические дроби.

Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.

Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.

Понятие рациональных чисел.

Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac\), где m – целое число, а n – натуральное число.

Другими словами, можно сказать:

Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Разберем каждый пункт подробно.

Множество рациональных чисел.

Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.

Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.

На рисунке можно показать множество рациональных чисел.

Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt\) или число \(\pi\) (читается число пи) не являются рациональными числами.

Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac\).

Докажите, что число \(\sqrt\) является рациональным?
Доказательство: \(\sqrt=0,07\)

Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.

Читайте также: