Что такое подмножество кратко
Обновлено: 07.07.2024
Как известно, множество является одним из важнейших элементов алгебры, а точнее – теории множеств. Это понятие не имеет строгого определения в силу своей аксиоматичности и фундаментальности, и передается на словах, как некий набор математических реальных чисел. Множества могут быть разными, включать большой спектр различных постоянных и переменных элементов, либо же вообще быть пустыми. Множество всех существующих определяемых чисел является бесконечным математическим множеством. А эфемерное множество, не содержащее никаких значимых объектов, именуется пустым.
В зависимости от свойств объектов, допускается выделение особых групп внутри множества. Например, рассмотрим бесконечное множество натуральных целых чисел, обозначенное как N. Выделим из него такие элементы, которые будут отвечать заданным свойствам – четность, и расположение в интервале от 1 до 11. Это числа 2, 4, 6, 8, 10. Эти пять элементов формируют особую группу, отвечающую общим свойствам, заданным в условии. При этом все члены группы принадлежат множеству натуральных чисел. Такие внутренние объединения именуются подмножествами.
Подмножество – это внутренняя группа элементов множества, все члены которой строго принадлежат данному множеству. Этот набор также принято обозначать большими латинскими группами – например, вышеуказанный пример из пяти элементов можно обозначить, как подмножество S. Стоит сразу отметить, что любое подмножество само по себе является независимым множеством. Приставка под- обозначает только факт принадлежности всех членов данной группы к более широкому набору элементов, относящихся к большому множеству. С другой стороны, такое объединяющее множество именуют надмножеством. Из нашего примера следует, что множество N натуральных чисел включает подмножество S чисел, отвечающих условиям четности, и расположения в интервале (1, 11). Иначе можно сказать, что множество S, состоящее из пяти натуральных чисел, относится к надмножеству N, содержащему все натуральные числа.
Взаимоотношения между различными группами элементов могут быть самыми разнообразными. То же множество натуральных чисел может включать практически бесконечное количество различных группировок – подмножеств. В фундаментальном определении теории множеств чисел существует два основных базиса: само множество, как набор элементов, и свойства, задающие этот набор, или описывающие его. Собственно говоря, эти свойства позволяют не только ограничить набор чисел во множестве, но и включить его в состав какого-либо надмножества либо же выделить из него подмножество.
В нашем видеоуроке мы также рассмотрим взаимосвязь между двумя различными независимыми множествами. Например, рассмотрим следующие множества произвольных чисел:
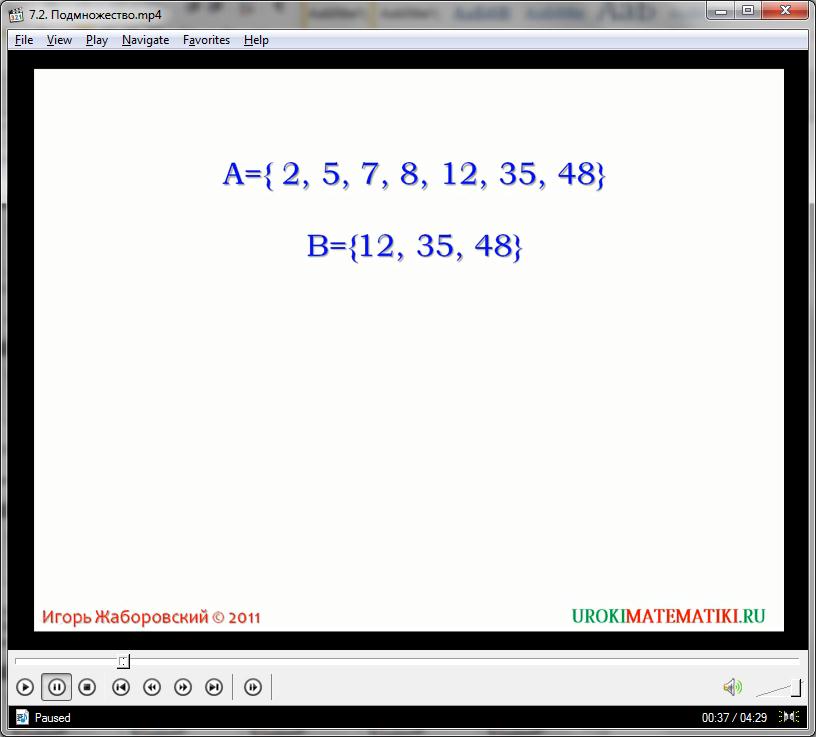
Все элементы множества D встречаются среди членов множеств и S и F. Можно сказать, что D является подмножеством множества S, и подмножеством множества F.
С другой стороны, все элементы множества S совпадают с элементами множества F. Соответственно, и наоборот. Можно обозначить, что S является подмножеством для F, а F, в свою очередь, является подмножеством для S. Но чаще всего говорят, что множества просто равны между собой.
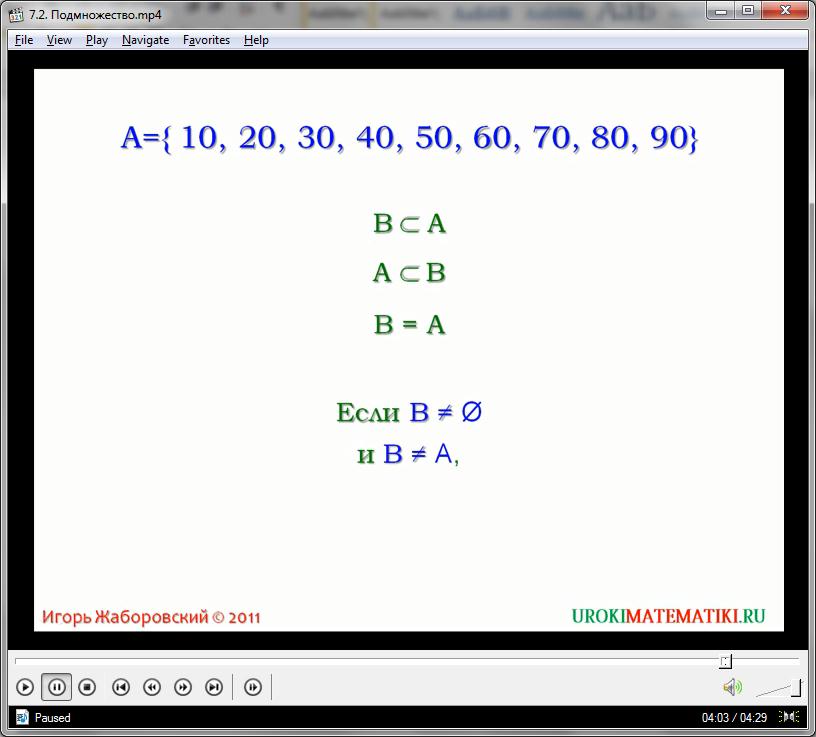
Если любое подмножество А не равно пустому множеству (т.е. содержит хотя бы один элемент), и при этом не равно другому множеству В, то считается, что подмножество А является собственным подмножеством для В. Пустое множество является собственным подмножеством для любого множества, кроме самого себя. С другой стороны, практически все реальные множества являются подмножествами бесконечного множества действительных чисел.
На геометрии подмножества отображаются двумя способами. Собственно геометрический представляет собой линейно-интервальный метод отображения наборов чисел на горизонтальной прямой. Чертится прямая (теоретически бесконечная – как отображение бесконечного надмножества чисел), на ней откладываются заданные числовые отрезки. Например, множество целых чисел от 2 до 10 образуют отрезок АС. Множество четных чисел, состоящих, например, из 2, 4, 6 являются подмножеством для АС, и задаются более коротким отрезком АВ, лежащим на той же прямой, на некотором участке АС.
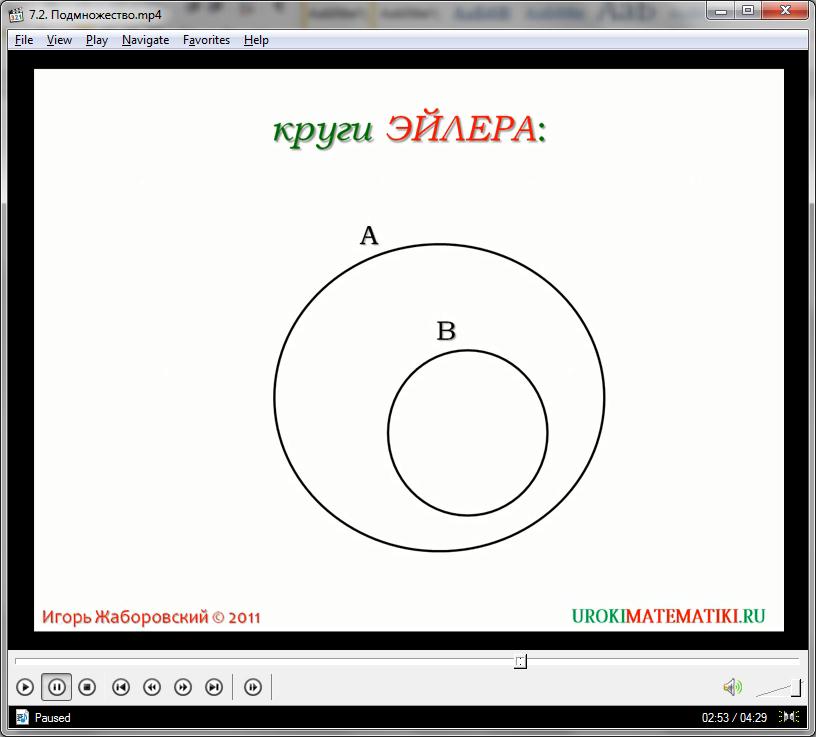
Но более удобным изображением подмножества являются круги Эйлера. В данном случае, каждое множество представлено правильным кругом. Подмножества выделяются меньшими кругами, вложенными в большой круг. Если подмножество равно самому множеству, то круги совпадают между собой. Если группа элементов не соотносится с каким-либо множеством, то круг группы выходит за пределы этого множества.
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Конечные множества
Бесконечные множества
Пустые множества
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
A = $\$ - множество всех действительных положительных x
B = $\$ - множество всех натуральных n, кратных 5
C = $\$ – множество всех действительных точек координатной плоскости (x,y), расстояние от которых до начала координат не больше 1 (круг с центром в начале координат, радиусом 1).
D = – множество всех материков планеты Земля
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Множество A называют подмножеством множества B (A $\subseteq$ B), если всякий элемент множества A также является элементом множества B:
$$ A \subseteq B \iff (a \in \Bbb A \Rightarrow a \in \Bbb B) $$
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Примеры подмножеств:
Множество людей является подмножеством приматов, живущих на Земле.
Множество натуральных чисел меньших 5 является подмножеством натуральных чисел меньших $10: A = \, B = \, A \subseteq B$
Множество квадратов является подмножеством прямоугольников.
Множество полосатых летающих слонов – как пустое множество - является подмножеством чего угодно: приматов, чисел, прямоугольников. Что удобно для размышлений о смысле всего.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Булеан конечного множества из n элементов содержит $2^n$ элементов:
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Задано множество натуральных чисел, входящих в полуинтервал $9 \lt n \le 12$.
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
г) Множество всех целых решений уравнения $x^3+x^2+4 = 0$
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Задано бесконечное множество точек, принадлежащих данной гиперболе $y = \frac$ в данном интервале $-4 \le x \le -1$. На графике:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 10 апреля 2012.

На диаграмме кругов Эйлера видно, что является подмножеством , а является надмножеством
Подмно́жество в теории множеств — это понятие части множества.
Содержание
Определение
Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:

Множество называется надмно́жеством множества , если — подмножество .
Существует два символических обозначения для подмножеств:

К сожалению, обе системы обозначений используют символ в разных смыслах, что может привести к путанице. В данной статье мы будем использовать последнюю систему обозначений.
То, что называется надмножеством , часто записывают .
Множество всех подмножеств множества обозначается A" width="" height="" />
и называется множеством-степенью.
Собственное подмножество
Любое множество является своим подмножеством. Если мы хотим исключить из рассмотрения, мы пользуемся понятием со́бственного подмножества, которое определяется так:
Множество является собственным подмножеством множества , если и .
Пустое множество является подмножеством любого множества. Если мы вдобавок хотим исключить из рассмотрения пустое множество, мы пользуемся понятием нетривиа́льного подмножества, которое определяется так:
Множество является нетривиальным подмножеством множества , если является собственным подмножеством и .
Примеры
Свойства
Отношение подмножества обладает целым рядом свойств [1] .
Подмножества конечных множеств
Если исходное множество конечно, то у него существует конечное количество подмножеств. А именно, у -элементного множества существует подмножеств (включая пустое). Чтобы убедиться в этом, достаточно заметить, что каждый элемент может либо входить, либо не входить в подмножество, а значит, общее количество подмножеств будет -кратным произведением двоек. Если же рассматривать только подмножества -элементного множества из элементов, то их количество выражается биномиальным коэффициентом " width="" height="" />
. Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать способами, второй способом, и так далее, и, наконец, -й элемент можно выбрать способом. Таким образом мы получим последовательность из элементов, и ровно таким последовательностям соответствует одно подмножество. Значит, всего найдется =\binom" width="" height="" />
таких подмножеств.
Примечания
- ↑В. А. Ильин , В. А. Садовничий , Бл. Х. Сендов . Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова . — 3-е изд. , перераб. и доп. — М .: Проспект, 2006. — Т. 1. — С. 65. — 672 с. — ISBN 5-482-00445-7
См. также
Ссылки
Логические операции с понятиями
Высказывание - построение над множеством
В - непустое множество, над элементами которого определены три операции: конъюнкция ( или &,бинарная) • дизъюнкция (,бинарная) • отрицание (,унарная)
Подмно́жество в теории множеств - это понятие части множества.
" width="" height="" />
является подмножеством " width="" height="" />
, а " width="" height="" />
является надмножеством " width="" height="" />
Содержание
Определения
Собственное подмножество
Из определения прямо следует, что пустое множество обязано быть подмножеством любого множества. Также, очевидно, любое множество является своим подмножеством:
Если " width="" height="" />
, и " width="" height="" />
то " width="" height="" />
называется со́бственным или нетривиа́льным подмножеством.
Свойства
Пример
Читайте также:


