Что такое неевклидова геометрия лобачевского кратко
Обновлено: 07.07.2024
Чтобы представить себе геометрию Лобачевского, лучше всего сравнить ее с привычной евклидовой.
А уж потом из этих аксиом чередой выводил вереницу теорем.
В этой стройной системе была закавыка — один постулат (пять аксиом Евклид назвал постулатами) выглядел неуклюже. Больше двух тысяч лет после Евклида математики пытались показать, что этот постулат лишний; что его можно вывести из остальных аксиом. Кто только этим не занимался: Омар Хайам, Лежандр, Бельтрами, Ламберт…
Лобачевский предположил другой постулат вместо пятого и надеялся из этого предположения вывести вереницу теорем так, чтобы какие-нибудь были противоречивы. Тогда можно было бы сделать вывод, что предположение ложное, а значит, пятый постулат Евклида истинный.
Так он выводил одну теорему за другой и в конце концов понял, что просто строит другую — неевклидову — геометрию. Ее утверждения казались парадоксальными:
- Сумма углов любого треугольника меньше 180°.
- Если углы двух треугольников попарно равны, то и треугольники равны.
- Подобных, но не равных треугольников не бывает.
И геометрия Евклида, и геометрия Лобачевского позволяют выводить цепочки непротиворечивых теорем. Но для геометрии Евклида у нас есть привычная модель: мы умеем рисовать точки и прямые, задавать углы и расстояния так, что все теоремы можно увидеть своими глазами. А для геометрии Лобачевского такой модели не было.
Как все нарисовать, придумали другие люди, и уже после смерти Лобачевского. Они создали модели геометрии Лобачевского. Модель — не то же самое, что геометрия. Модель позволяет нам представить и увидеть, что происходит в плоскости Лобачевского — а увиденное уже проще понять. Чтобы представить себе геометрию Лобачевского, надо отказаться от представления, что плоскость выглядит как бесконечный во все стороны лист бумаги, что прямая выглядит так:
В модели Пуанкаре на диске, например, плоскость выглядит как круг без края:
Представьте себе, что на этой плоскости живут коротышки, и что размеры всех объектов на плоскости уменьшаются при удалении от центра. Идет такой коротышка от центра к абсолюту (так называется край), и становится все меньше и меньше, а ножки у него все короче и короче. Идет он, идет, а до края дошагать никак не может — чем ближе к краю, тем ближе длина шага к нулю. А раз до края дойти не может, плоскость кажется ему бескрайней.
Точки в его мире выглядят так же, как в нашем. А прямыми в его мире считаются евклидовы диаметры диска и куски евклидовых окружностей, перпендикулярных абсолюту, несколько прямых нарисованы синим. В такой геометрии можно определить углы между прямыми, расстояния и преобразования, которые сохраняют расстояния.
С теоретической точки зрения геометрии Евклида и Лобачевского равноправны. А вот какая из них верно описывает наш мир — большой вопрос. Многое зависит от масштаба. Мы с вами знаем, что поверхность Земли больше похожа на шар, чем на плоскость; но размечая грядки на даче, мы об этом не думаем, для дачного масштаба хватает плоского приближения. Наш бытовой жизненный опыт говорит нам, что мы живем на плоскости; чтобы увидеть шар, надо перейти к планетарным масштабам.
Сам Лобачевский проводил астрономические наблюдения и вычисления, но его результаты не были достаточно аккуратны, чтобы определить, какая именно геометрия реализуется в нашем мире. Собственно говоря, науке до сих пор это неизвестно наверняка.

В Казани много лет проработал великий математик Н.И. Лобачевский. Он был не только ученым, но и прекрасным организатором

Пятый постулат Лобачевского утверждает, что через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие ее, в то время как в евклидовой геометрии через эту точку можно провести только одну такую прямую.
Иногда ошибочно думают, что в геометрии Лобачевского две параллельные прямые пересекаются, но это не так. Более того, в неевклидовой геометрии вообще ничего не говорится о параллельных прямых — только о непересекающихся. Дело в том, что пространство, в котором действует геометрия Лобачевского, обладает отрицательной кривизной. Такое пространство можно вообразить, если представить себе геометрические тела, похожие на воронку и седло. Во всяком случае, неевклидова геометрия, в отличие от евклидовой, реализуется в искривленном пространстве. А ведь сейчас считается, что пространство нашей Вселенной обладает кривизной. Связана неевклидова геометрия и с теорией относительности Эйнштейна. А евклидова геометрия тоже верна, но является ее частным случаем.

Еще одна геометрия
В науке известны три великие геометрии — Евклида, Лобачевского и Римана. Геометрия Римана реализуется на сфере, и там все прямые пересекаются. Но их при этом нельзя назвать параллельными. Дело в том, что параллельные прямые, согласно своему определению, не пересекаются ни в одной геометрии.
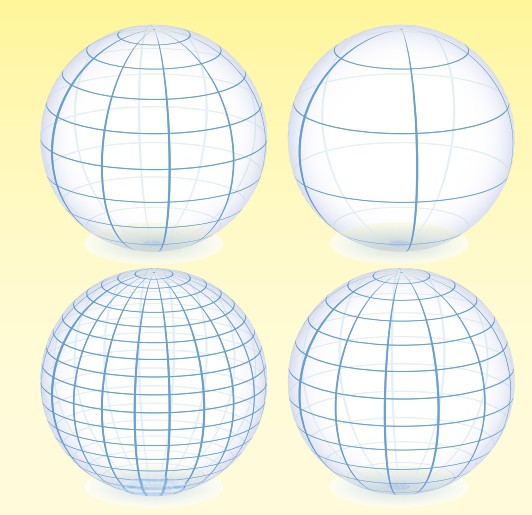
В сферической геометрии Римана пересекаются все прямые, но никакие из них, по условию, не являются параллельными

195 лет назад (11 (23) февраля 1826 г.) на заседании физико-математического факультета Императорского Казанского университета Николай Иванович Лобачевский впервые представил общественности неевклидову геометрию.
Николай Лобачевский заменил пятый постулат Евклида на противоположное утверждение: если из точки, не лежащей на прямой, выпустить все лучи, пересекающие эту прямую, то слева и справа эти лучи будут ограничены двумя предельным лучами, которые прямую уже не пересекут, но будут становиться к ней все ближе и ближе, а угол между этими предельными лучами будет строго меньше 180 градусов; то есть через точку, не лежащую на данной прямой, можно провести не одну прямую, параллельную данной (как у Евклида), а сколько угодно, причем эти прямые будут вести себя иначе, чем в трактовке Евклида.
Геометрия Лобачевского стала толчком к переосмыслению природы пространства. Можно сказать, что работа ученого подготовила условия для создания общей теории относительности, ведь раньше у нас была только одна геометрия и одно понимание пространства, но это в корне изменилось благодаря нашему соотечественнику.
Спустя три года после выступления в Казанском университете Лобачевский опубликовал статью о своей геометрии в университетском журнале. Как уже отмечалось выше, поначалу многие отнеслись к работе ученого критически; потребовались годы, чтобы неевклидова геометрия отвоевала себе место под Солнцем.
Неевклидова геометрия в каком-то смысле разделила науку на до и после, но эта работа отнюдь не единственный вклад Николая Лобачевского в развитие научной мысли. Независимо от бельгийского математика Жерминаля Данделена Лобачевский разработал метод приближенного решения уравнений, уточнил понятие непрерывной функции, написал работы о тригонометрических рядах, предложил признак сходимости числовых рядов и опубликовал немало других важных трудов.
Подготовлено по материалам:
● Н. И. Лобачевский, Геометрические исследования по теории параллельных линий. Перевод, комментарии, вступительные статьи и примечания профессора В. Ф. Кагана. М.-Л., изд-во Академии Наук СССР, 1945.

Возникновение геометрии Лобачевского
Вот неполный перечень учёных, занимавшихся доказательством V постулата до 19 в.: древнегреческий математики Птолемей (2 в.), Прокл (5 в.) (доказательство Прокла основано на предположении о конечности расстояния между двумя параллельными), Ибн аль-Хайсам из Ирака (конец 10 — начало 11 вв.) (Ибн аль-Хайсам пытался доказать V постулат, исходя из предположения, что конец движущегося перпендикуляра к прямой описывает прямую линию), таджикский математик Омар Хайям (2-я половина 11 — начало 12 вв.), азербайджанский математик Насирэддин Туей (13 в.) (Хайям и Насирэддин при доказательстве V постулата исходили из предположения, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения), немецкий математик К. Клавий (Шлюссель, 1574), итальянские математики П. Катальди (впервые в 1603 напечатавший работу, целиком посвященную вопросу о параллельных), Дж. Борелли (1658), Дж. Витале (1680), английский математик Дж. Валлис (1663, опубликовано в 1693) (Валлис основывает доказательство V постулата на предположении, что для всякой фигуры существует ей подобная, но не равная фигура). Доказательства перечисленных выше геометров сводились к замене V постулата др. предположением, казавшимся более очевидным.
Итальянский математик Дж. Саккери (1733) сделал попытку доказать V постулат от противного. Приняв предложение, противоречащее постулату Евклида, Саккери развил из него довольно обширные следствия. Ошибочно признав некоторые из этих следствий приводящими к противоречиям, Саккери заключил, что постулат Евклида доказан. Немецкий математик И. Ламберт (около 1766, опубликовано в 1786) предпринял аналогичные исследования, однако он не повторил ошибки Саккери, а признал своё бессилие обнаружить в построенной им системе логическое противоречие. Попытки доказательства постулата предпринимались и в 19 в. Здесь следует отметить работы французского математика А. Лежандра; одно из его доказательств (1800) основано на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла, т. е., как и все его предшественники, он заменил постулат др. допущением. Довольно близко к построению Лобачевского геометрия подошли немецкие математики Ф. Швейкарт (1818) и Ф. Тауринус (1825), однако ясно выраженной мысли о том, что намечаемая ими теория будет логически столь же совершенна, как и геометрия Евклида, они не имели.
Приведём несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским
1) В Лобачевского геометрия не существует подобных, но неравных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, например, сторона правильного треугольника с данной суммой углов.
2) Сумма углов всякого треугольника меньше p и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность p — (a + b + g), где a, b, g — углы треугольника, пропорциональна его площади.
3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих а и находящихся с ней в одной плоскости; среди них есть две крайние b, b`, которые и называются параллельными прямой а в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) а общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек) (рис. 1,3). Угол ее между прямой b (или b`) и перпендикуляром из О на а — т. н. угол параллельности — по мере удаления точки О от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель b с одной стороны (а b` с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).
4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.
5) Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.
6) Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.
7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.
8) Длина окружности не пропорциональна радиусу, а растет быстрее.
Лобачевского геометрия продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы фигур, общая теория кривых и поверхностей и т. п. Ряд геометров развивали также механику в пространстве Лобачевского. Эти исследования не нашли непосредственных применений в механике, но дали начало плодотворным геометрическим идеям. В целом Лобачевского геометрия является обширной областью исследования, подобно геометрии Евклида.
Читайте также:

