Что представляет собой нитяной маятник кратко
Обновлено: 05.07.2024
Нитяной маятник – физическая модель, в которую включают невесомую нерастяжимую нить и тело, размеры которого пренебрежимо малы по сравнению с длиной нити, находящиеся в силовом поле, как правило, гравитационном поле Земли или другого небесного тела.
Период малых колебаний нитяного маятника пропорционален квадратному корню из длины нити и обратно пропорционален квадратному корню из коэффициента силы тяжести.
Информация предоставлена для ознакомления и не является официальным источником.
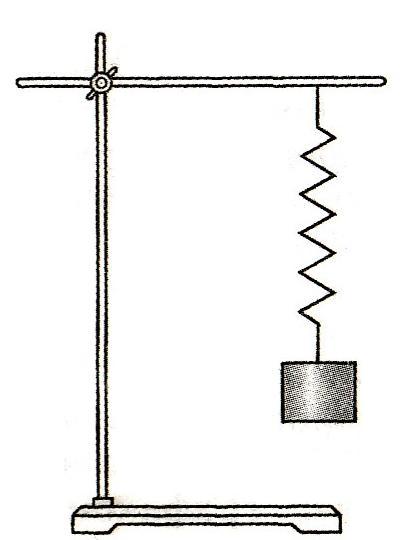
Познакомимся с физической моделью нитяной маятник. Взгляните на рисунок. Вы видите кирпич, подвешенный на широкой ленте, и тяжёлый шарик, подвешенный на нити. Толкнём их рукой, и оба тела начнут совершать колебания – станут маятниками.
Изучить колебания – значит найти способы описания колебаний и выявить их закономерности. Удобен ли для этого кирпичный маятник? Конечно, нет. Во-первых, потому, что он большой, и при его качаниях будет велика сила сопротивления воздуха. Во-вторых, лента подвешена за два конца, и при качаниях её половины будут натягиваться неодинаково, из-за чего кирпич будет двигаться зигзагами. Тяжёлый шарик на нити более удобен для изучения колебаний.
Нитяным маятником называют тело на невесомой нерастяжимой нити, совершающее колебания. Для этой модели важно, чтобы размеры тела были малы по сравнению с длиной нити. В таком случае говорят: формой и размерами тела можно пренебречь (то есть в данных условиях не принимать их во внимание).
Опыты показывают: если на тело нитяного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной нити (говорят: маятник совершает малые колебания), то период колебаний нитяного маятника можно подсчитать по формуле, которая помещена в рамке.
Вы видите, что период малых колебаний нитяного маятника не зависит от его массы, а определяется лишь длиной нити l и коэффициентом g. Например, при увеличении длины нити в 4 раза, период колебаний маятника возрастёт в 2 раза (что равно √4 раз).
Рассмотрим вторую модель: пружинный маятник – тело на пружине, совершающее колебания. При этом важно, чтобы один конец пружины был закреплён, а её масса была мала по сравнению с массой тела (то есть массой пружины можно было бы пренебречь).
Опыты показывают: если на тело пружинного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной пружины (то есть она деформируется упруго), то период колебаний пружинного маятника можно подсчитать по формуле, которая помещена в рамке.
Итак, период малых колебаний пружинного маятника не зависит от коэффициента силы тяжести, а определяется лишь массой тела m и коэффициентом k, характеризующим жёсткость пружины. Например, при увеличении массы груза в 9 раз, период колебаний маятника возрастёт в 3 раза (что равно √9 раз).
Наряду со свободными колебаниями, когда маятник выведен из положения равновесия и предоставлен самому себе, существуют также вынужденные колебания и автоколебания. Обратимся к рисунку. Под гирей, висящей на пружине, расположен электромагнит. Если мы будем попеременно включать и выключать ток, то гиря начнёт совершать вынужденные колебания, частота которых зависит от частоты внешнего воздействия.
Однако маятник может сам регулировать поступление энергии, совершая автоколебания. Взгляните: средний провод зажат прищепкой и касается гири, пока она вверху. Ток, проходя через пружину, гирю, средний провод и электромагнит, намагничивает его сердечник. Притягиваясь, гиря движется вниз. Вскоре она отсоединяется от среднего провода, ток прекращается, и магнитное поле исчезает. Под действием пружины гиря поднимается вверх и снова замыкает цепь.
Представьте себе маятник часов, бабочку, взмахивающую крыльями, иглу швейной машины и отбойный молоток. На первый взгляд совершенно разные предметы, но с точки зрения физики у них есть одна общая черта. Об этом и не только поговорим в данном уроке.
План урока:
Колебательное движение
В самом широком смысле, колебательное движение – это любое движение, повторяющееся с течением времени. Например, птица, машущая крыльями вверх-вниз, совершает ими колебательные движения. Ребенок, качающийся на качелях, тоже совершает колебательные движения. Игла швейной машины при шитье – тоже.
Но как же так, ведь в названных примерах тела движутся абсолютно по-разному? Крылья птицы и игла швейной машины движутся вертикально вверх-вниз (прямолинейно), ребенок на качелях движется горизонтально и по дуге (криволинейно). Это все неважно. Главный признак колебательного движения – его повторяемость через определенный промежуток времени, то есть через период колебаний.
Период и частота колебаний
Период колебаний (T) – это время, за которое тело совершает полный цикл движения, т.е. совершает одно колебание.
В случае с движением крыльев птицы, если считать, что один взмах начинается с верхней точки, полным колебанием будет считаться, когда крылья пройдут от верхней точки через середину до нижней и вернутся от нижней точки через середину до верхней (рисунок 1).
Рисунок 1 – Взмах крыльев птицы как пример полного колебания
Период колебаний обозначается латинской буквой T. По определению период – это время, значит, единица измерения периода будет такой же, как и единица измерения времени. В СИ это секунда.
Как же можно вычислить период колебаний?
Самый простой способ – это посчитать количество колебаний и секундомером измерить время, за которое эти колебания были совершены. Например, ребенок на качелях совершает N = 10 колебаний за t = 30 секунд. Нетрудно подсчитать, что время совершения одного полного колебания будет 30/10 = 3 с. Если обобщить, получится формула для нахождения периода колебаний:
где t – время, за которое совершено N колебаний.
Рассмотрим еще одну важную характеристику.
Частота колебаний (ν) – это количество колебаний, совершаемое телом за единицу времени.
Если сравнить определение частоты колебаний с определением периода, можно заметить, что это обратные величины. То есть:
Гц – единица измерения, которую назвали в честь немецкого физика Генриха Герца. При решении задач одинаково часто употребляется и герц, и с -1 . Можно употреблять и то, и другое – в зависимости от того, что удобнее при решении конкретной задачи.
Следует так же отметить, что иногда физики пользуются циклической частотой колебаний:
Свободные колебания
Положение равновесия при колебательном движении
Сравним две ситуации:
1. Родитель толкает качели, на которых сидит ребенок, а потом просто наблюдает, как качели качаются сами по себе.
2. Родитель толкает качели с ребенком, а потом при каждом цикле движения подталкивает качели, поддерживая качания.
Физики говорят, что в первом случае система (качели и ребенок) совершает свободные колебания, то есть колебания под действием только внутренних сил. После выведения системы из равновесия (то есть толчка родителя) к ней больше не прикладывают внешних сил. Во втором случае говорят, что система совершает вынужденные колебания – то есть колебания, под действием периодического внешнего воздействия.
Поговорим о свободных колебаниях. Для простоты рассмотрим систему, состоящую из маленького тяжелого шарика на длинной крепкой нити. Такая система называется нитяным маятником (рисунок 2).
Рис.2 – Нитяной маятник
Без воздействия внешних сил шарик будет находиться в положении 1. Такое состояние называется положением равновесия. Далее к шарику прикладывают силу, направленную влево и он начинает совершать колебания. Траектория шарика будет: 1-2-1-3-1 (см. рисунок 1).
Как при этом будет меняться скорость тела? Для того, чтобы рассмотреть подробно, нужно помнить определения потенциальной и кинетической энергии*, а также в чем заключается закон сохранения энергии (систему считаем замкнутой – потерь энергии не происходит, а, значит, закон сохранения энергии выполняется – энергия колебательной системы остается постоянной):
- при движении из точки 1 в 2 шарик постепенно замедляется (уменьшается его кинетическая энергия, а потенциальная увеличивается);
- в точке 2 он на мгновенье останавливается (кинетическая энергия равна нулю, потенциальная максимальна);
- далее он начинает движение с ускорением, но уже в обратном направлении (кинетическая энергия увеличивается, потенциальная уменьшается) - при движении из 2 в 1 тело будет ускоряться;
- когда шарик дойдет до точки 1 его кинетическая энергия будет максимальна, а потенциальная минимальна.
При движении от точки 1 в 3 будет происходить то же самое, что и при движении из 1 в 2 – предлагаем описать процесс изменения величин (скорости и энергии) самостоятельно.
Если обобщить все сказанное, можно сделать вывод: при колебаниях в положении равновесия кинетическая энергия тела максимальна, а потенциальная минимальна (или равна нулю, в зависимости от выбранной точки отсчета). В крайних положениях потенциальная энергия максимальна, а кинетическая равна нулю. То есть положение равновесия маятника – это такое положение, в котором его потенциальная энергия минимальна (или равна нулю, в зависимости от точки отсчета). При удалении маятника от положения равновесия кинетическая энергия будет уменьшаться, а потенциальная увеличиваться.
*Потенциальная энергия тела зависит от его положения в пространстве; кроме того, это относительная величина – она зависит от того, какая точка отсчета выбрана.
Кинетическая энергия зависит от модуля скорости тела.
Амплитуда колебаний
Помимо частоты и периода важной характеристикой колебаний является амплитуда.
Амплитуда колебаний – это модуль максимального смещения тела от положения равновесия. Другими словами, это расстояние между положением равновесия и крайней точкой траектории маятника. Рассмотрим рисунок 3. На нем изображен уже знакомый вам нитяной маятник. В идеальном случае амплитуду колебаний маятника нужно считать как длину дуги от положения равновесия до крайней точки. Но если мы считаем, что колебания малые – то есть длина нити маятника (l) гораздо больше смещения (S), можно считать, что длина дуги совпадает с длиной отрезка между проекциями положения равновесия и крайней точки на ось ОХ.
Рис.3 – Амплитуда колебаний нитяного маятника
Обычно амплитуда обозначается большой латинской буквой A.
Колебательные системы
Для того, чтобы рассмотреть колебательные движения подробнее, рассмотрим несколько колебательных систем, на примере которых будет рассматривать все закономерности.
1. Маятник
В общем случае маятник – это система, способная совершать колебания под действием каких-либо сил, например, сил трения, упругости, тяжести.
2. Пружинный маятник
Пружинный маятник – это система, состоящая из упругой пружины, один конец которой закреплен, а на другой прикреплен груз.
Такой маятник может быть вертикальным (рисунок 4а), тогда колебания будут совершаться под действием сил тяжести и упругости; и горизонтальным (рисунок 4б), тогда на груз будут действовать сил упругости и трения.
Рис.4 – Пружинный маятник
Для пружинного маятника справедливы формулы:
где T –период колебаний пружинного маятника; π ~ 3.14; m–масса груза;k–коэффициент жесткости пружины; - частота колебаний пружинного маятника.
*Ранее говорилось, что существует такая характеристика, как циклическая частота. Формула для ее нахождения будет выглядеть так:
3. Нитяной маятник
Этот вид маятника уже рассматривался ранее (см. рисунок 3), он состоит из длинной нити и тяжелого грузика, подвешенного на ней.
Для нитяного маятника справедливы формулы:
где T – период колебаний нитяного маятника; π ~ 3.14; l –длина нити; g – ускорение свободного падения (~9,8 м/с 2 ), v - частота колебаний.
Интересно отметить, что период нитяного маятника и, следовательно, его частота не зависят от массы грузика, прикрепленного к нити.
*Следует отметить, что все приведенные формулы справедливы только для малых колебаний.
** Циклическая частота нитяного маятника:
Гармонические колебания
При решении задач часто используется не нитяной маятник, а его упрощенная модель – математический маятник. Это идеальная колебательная система, в которой нить считается очень длинной по сравнению с амплитудой колебаний и размерами грузика; сам груз достаточно тяжелым, чтобы пренебречь массой нити. Кроме того, считается, что не происходит потерь энергии.
Рассмотрим подробно, какие силы действуют на такую систему. В первую очередь, на грузик действует сила тяжести mg, направленная вниз (см. рисунок 5). Так же на него действует сила натяжения со стороны нити F, она направлена вдоль нити. Обозначим угол, на который смещается тело от положения равновесия.
Рис.5 – Силы, действующие на математический маятник
Запишем 2-й закон Ньютона:
Рисунок 6 – Силы, действующие на математический маятник при смещении на угол φ
В случае малых углов sinφ можно считать равным φ. Из геометрического определения синуса:
Тогда в крайней точке 2-й закон Ньютона в проекции на ось OX перепишется следующим образом:
То есть ускорение, с которым движется маятник прямо пропорционально его смещению от положения равновесия. Минус в данном выражении означает, что ускорении направлено в противоположную сторону от смещения.
Интересно заметить, что ускорение грузика, подвешенного к ниточке (а значит и самого маятника), не зависит от его массы. Период колебаний математического маятника тоже не зависит от массы грузика:
В случаях, когда колебания происходят под действием силы, пропорциональной смещению тела от положения равновесия, говорят, что тело совершает гармонические колебания.*
График зависимости смещения от времени при гармоническом колебательном движении представляет собой синусоиду или косинусоиду (см. рисунок 7).
Рис. 7 – График зависимости смещения (x) от времени (t) при гармонических колебаниях
На графическом представлении колебаний (рисунок 7) удобно находить период и амплитуду гармонических колебаний.
*Могло сложиться впечатление, что гармонические колебания может совершать только математический маятник. Это не так. Любое тело может совершать колебания, близкие к гармоническим (нужно учитывать не идеальность систем). Например, можно говорить о гармонических колебаниях пружины, если она достаточно жесткая, чтобы она деформировалась упруго, а колебания совершаются с небольшой амплитудой.
Величины, характеризующие колебательное движение
Ранее рассматривались такие характеристики колебаний, как период, частота и амплитуда. Помимо этих величин, колебания характеризуются фазой колебаний.
Фаза колебаний
На рисунке 7 изображен график зависимости смещения от времени при гармонических колебаниях. Такой график называется синусоидой (косинусоидой). В общем случае уравнение зависимости координаты Х от времени t будет выглядеть так:
Разность фаз
Найдем разность фаз колебаний этих двух маятников.
Если взять конкретный момент времени , фаза гармонических колебаний каждого из маятников в этот момент времени будет:
- это начальные фазы колебания первого и второго маятников соответственно. Эти величины являются начальными условиями, и они не изменяются во время движения, следовательно, при одинаковой частоте колебаний маятников разность фаз остается постоянной.
Затухающие колебания
Во всех рассмотренных ранее случаях считалось, что на колеблющуюся систему не действуют силы извне. На самом деле, идеальных систем не существует, поэтому любой маятник во время движения будет преодолевать внешние силы сопротивления и терять энергию. Например, пружинный маятник (рисунок 8) будет преодолевать силу трению о поверхность.
Рисунок 8 – Пружинный маятник на шероховатой поверхности
Колебания, энергия которых уменьшается с течением времени, называются затухающими.
Амплитуда затухающих колебаний уменьшается со временем. График таких колебаний изображен на рисунке 9.
Рисунок 9 – График зависимости координаты от времени при затухающих колебаниях
Вынужденные колебания
Собственная частота колебаний. Частота вынуждающей силы. Установившиеся вынужденные колебания
В реальных (неидеальных) системах колебания всегда нужно поддерживать внешним воздействием.
Под действием периодической внешней изменяющейся силы возникают вынужденные колебания.
Почему же обязательно сила должны быть периодически изменяющейся? Ответ на этот вопрос легко найти, представив себе качели. Если на них действовать с постоянной по модулю и направлению силой, они никогда не начнут качаться. А толчками (то есть периодической изменяющейся силой) раскачать их не составит труда.
Внешняя сила, заставляющая систему совершать колебания, называется вынуждающей силой.
Так как эта сила периодическая, необходимо ввести частоту вынуждающей силы. А чтобы не запутаться, частоту свободных колебаний называют собственной частотой системы. Как показывают эксперименты, даже если изначально собственная частота системы и частота вынуждающей силы отличались, через некоторое время система начинает колебаться с частотой вынуждающей силы. В таких случаях говорят об установившихся вынужденных колебаниях.
Если частота вынуждающей силы равна собственной частоте системы, возникает резонанс – резкое увеличение амплитуды колебаний.
Механические колебания
Колебания являются очень распространенным видом движения. Это покачивание веток деревьев деревьев на ветру, качание маятника в настенных часах, волны на воде. Рассмотрим колебательное движение на примере двух маятников.
Нитяной маятник представляет собой шарик, прикрепленный к тонкой, легкой нити. Если шарик сместить в сторону, и отпустить, то он периодически начнет колебаться.
Пружинный маятник представляет собой груз, способный колебаться под действием силы упругости пружины.
Колебательные движения характеризуют амплитудой, периодом и частотой колебаний.
Амплитуда колебаний - это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия.
Период колебаний - это время, за которое совершается одно колебание.
Чтобы найти частоту колебаний, нужно время, за которое совершено несколько колебаний, разделить а число этих колебаний.
Частота колебаний - это число колебаний, совершаемых за одну секунду.
Чтобы найти частоту колебаний, надо число колебаний разделить на время, в течение которого они произошли.
Остальные уроки
Читайте также: