Что называется механической системой кратко

Обновлено: 04.07.2024

$\vec<F> = \frac<\mathrm<d>><\mathrm<d>t>(m \vec)$

Второй закон Ньютона

Классическая механика дает очень точные результаты в рамках повседневного опыта. Но для систем, движущихся с большими скоростями, приближающимися к скорости света, более точные результаты дает релятивистская механика, для систем микроскопических размеров — квантовая механика, а для систем, обладающих обеими характеристиками — квантовая теория поля. Тем не менее, классическая механика сохраняет свое значение, поскольку (1) она намного проще в понимании и использовании, чем остальные теории, и (2) в обширном диапазоне она достаточно хорошо приближается к реальности. Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и даже многих микроскопических объектов, таких как органические молекулы.

Содержание

Описание теории

Перейдем к изложению основных понятий классической механики. Для простоты, мы будем рассматривать только материальную точку, т. е. тело, размером которого можно пренебречь. Движение материальной точки характеризуется несколькими параметрами: её положением, массой, и приложенными к ней силами. Рассмотрим каждый из них по очереди.

В действительности, любое тело, которое подчиняется законам классической механики, обязательно имеет ненулевой размер. Настоящие материальные точки, такие, как электрон, подчиняются законам квантовой механики. Тела ненулевого размера могут испытывать более сложные движения, поскольку может меняться их внутренняя конфигурация, например, потому что теннисный мяч может двигаться, вращаясь. Тем не менее, мы сможем применить к подобным телам результаты, полученные для материальных точек, рассматривая такие тела, как совокупности большого количества взаимодействующих материальных точек. Мы сможем показать, что такие сложные тела ведут себя, как материальные точки, при условии, что они малы в масштабах рассматриваемой задачи.

Радиус-вектор и его производные

Радиус-вектор материальной точки указывает на её положение по отношению к произвольной точке, зафиксированной в пространстве, которая обычно называется началом координат, и обозначается O. Это вектор r соединяющий начало координат с частицей. В общем случае, материальная точка движется, поэтому r является функцией t, промежутка времени прошедшего с произвольного начального момента. Скорость изменения положения со временем, определяется так:

$\mathbf<v> = <d\mathbf<r>\over dt>$
.

Ускорение, или скорость изменения скорости, это:

$\mathbf= <d\mathbf<v> \over dt>$
.

Второй закон Ньютона

Второй закон Ньютона связывает массу и скорость частицы с векторной величиной, известной как сила. Пусть m — масса тела и F — векторная сумма всех приложенных к нему сил (то есть равнодействующая сила.) Тогда второй закон Ньютона выглядит так:

$\mathbf<F> = <d(m \mathbf<v>) \over dt>$
.

Величина mv называется импульсом. В большинстве случаев, масса m не изменяется со временем, и закон Ньютона можно записать в упрощенной форме

$\mathbf<F> = m \mathbf$

где a — ускорение, определенное выше. Не всегда выполняется условие независимости массы от времени. Например, масса ракеты уменьшается по мере использования горючего. В таких случаях последнее выражение неприменимо, и следует пользоваться полной формой второго закона Ньютона.

Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы F, полученное из рассмотрения сущности физического взаимодействия, в котором участвует тело. Например, сила трения может быть смоделирована как функция скорости частицы, а именно

$\mathbf<F> _ = - \lambda \mathbf$

где λ — некоторая положительная постоянная. Получив независимое выражение для каждой силы, действующей на тело, мы можем подставить его во второй закон Ньютона и получим дифференциальное уравнение, называемое уравнением движения. Продолжая наш пример, примем, что на тело действует только сила трения. Тогда уравнение движения будет иметь вид

$- \lambda \mathbf<v> = m \mathbf = m <d\mathbf<v>\over dt>$
.

Это можно интегрировать, что даст

$\mathbf = \mathbf_0 e^$

где v₀ — начальная скорость. Это означает, что скорость тела экспоненциально уменьшается со временем до нуля. Проинтегрировав последнее выражение, мы можем получить радиус-вектор r тела, как функцию времени.

Важными силами являются сила всемирного тяготения и сила Лоренца для электромагнетизма. Помимо этого, для определения сил, действующих на тело, используется третий закон Ньютона: если мы знаем, что тело A действует с силой F на тело B, значит B должно действовать с равной по величине и противоположной по направлению силой реакции, −F, на A.

Энергия

Если сила " width="" height="" />
приложена к частице, которая перемещается на " width="" height="" />
, то работа, совершенная силой, определяется как скалярное произведение силы и вектора перемещения:

$W = \vec<F> \cdot\Delta\vec.$

Если масса частицы постоянна, а W_total полная работа, совершенная частицей, определяемая как сумма работ совершенных приложенными к частице силами, то второй закон Ньютона примет вид:

W_total = ΔE_k,

где E_k называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до скорости v :

$E_k = \frac<1> mv^2$

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Сила называется потенциальной, если существует скалярная функция, известная как потенциальная энергия и обозначаемая E_p , такая что

$\vec<F> = - \vec E_p.$

Если все силы, действующие на частицу консервативны, и E_p является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

$\vec<F>\cdot \Delta \vec = - \vec E_p \cdot \Delta \vec = - \Delta E_p \Rightarrow - \Delta E_p = \Delta E_k \Rightarrow \Delta (E_k + E_p) = 0 \,\!$
.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

$\sum E = E_k + E_p \,\!$

является постоянной относительно времени. Это очень полезно, потому что часто приходится сталкиваться с консервативными силами.

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - , а внутренние - .

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Внутренние силы обладают следующими свойствами:

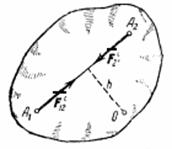
1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.31) действуют друг на друга с равными по модулю и противоположно направленными силами и , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Внутренние силы обладают следующими свойствами:

Одним из основных понятий механики является понятие механической системы. Под механической системой понимают совокупность конечного или бесконечного числа материальных точек (или тел), взаимодействующих между собой в соответствии с третьим законом Ньютона. Отсюда следует, что движение каждой точки (или тела) системы зависит как от положения, так и от движения остальных точек рассматриваемой механической системы.

Системы различают свободные и несвободные. Система называется свободной, если все входящие в нее точки могут занимать произвольные положения и иметь произвольные скорости. В противном случае, т. е. когда материальные точки, входящие в систему, не могут занимать произвольных положений или же не могут иметь произвольных скоростей, система называется несвободной.

Примером свободной механической системы может служить солнечная система, в которой Солнце и планеты можно рассматривать как материальные тела, находящиеся под взаимным действием сил ньютонианского притяжения.

Примером несвободной системы может служить система, состоящая из точек, из которых одна или

несколько вынуждены при своем движении оставаться на каких-либо линиях или поверхностях.

С указанным делением систем на свободные и несвободные связано понятие связи.

Под связью в механике понимают условия, накладывающие ограничения на свободу перемещения точек системы. Связи могут накладывать ограничения как на положения точек, так и на их скорости. Практически связи осуществляются с помощью материальных тел или приспособлений (стержней, нитей, шарниров и т. п.).

Подобно тому как силы, действующие на точки системы, подразделяют на силы внутренние и силы внешние, так и связи, наложенные на точки системы, можно подразделить на связи внутренние и связи внешние. Под внутренними связями понимают такие связи, которые будучи наложены на точки системы, не препятствуют системе свободно перемещаться после того, как она внезапно отвердеет. Связь, не обладающая этим свойством, называется внешней. Например, если две точки твердого тела соединены между собой нерастяжимым и невесомым стержнем, то такая связь будет внутренней. Таким образом твердое тело можно рассматривать как систему, подчиненную внутренним связям. Если же одна из точек твердого тела шарнирно закреплена, то в этом случае связь будет внешней.

Система, подчиненная одним лишь внутренним связям, является свободной, так как она может перемещаться как свободное твердое тело. Если же в числе связей, наложенных на точки системы, имеются внешние связи, то система является несвободной.

Условия, ограничивающие свободу перемещения точек системы, аналитически выражаются в виде уравнений или неравенств вида.

где — время, — соответственно координаты и скорости точки системы,

отнесенные к некоторой инерциальной системе отсчета, относительно которой рассматривается движение данной системы.

Связи различают удерживающие и неудерживающие; первым соответствует знак равенства в (1.1), вторым — знак неравенства.

Удерживающие и неудерживающие связи иногда соответственно называют двухсторонними и односторонними связями. Удерживающая связь, препятствуя перемещению в одном направлении, препятствует также перемещению в противоположном направлении. Неудерживающая связь препятствует перемещению в одном направлении, но не препятствует перемещению в противоположном направлении.

Примером удерживающей связи могут служить две параллельные плоскости, между которыми происходит движение шарика. Рассматривая среднюю между ними плоскость как координатную плоскость получаем уравнение связи в виде: Если же шарик движется по горизонтальной плоскости любой момент может покинуть ее, то эта плоскость будет являться неудерживающей связью. Условие такой связи будет выражаться неравенством (или ).

Другим примером неудерживающей связи может служить нить с шариком на конце. Принимая точку подвеса нити за начало координат и считая нить нерастяжимой, можем условие этой связи записать в виде неравенства

где — координаты шарика, — длина нити.

Если в процессе движения шарика выполняется неравенство

то это означает, что нить ослаблена и шарик освободился от связи.

Если же при движении шарика выполняется равенство

то это означает, что нить натянута, и на шарик действует связь.

В зависимости от того, содержит ли уравнение связи в явном виде время или нет, связи подразделяются на нестационарные (реономные) и стационарные (склерономные).

Связи, которые накладывают ограничения только на положения точек системы, называются конечными или геометрическими; аналитически они выражаются уравнением

Здесь и в дальнейшем предполагаем связи удерживающими.

Если же связи накладывают ограничения не только на положения точек, но и на их скорости, то они называются дифференциальными или кинематическими, и их аналитическое выражение имеет вид

Связи подразделяют также на голономные и неголономные. К голономным связям относят все конечные или геометрические связи вида (1.2), т. е. все связи, которые накладывают ограничения на возможные положения точек системы. К голономным связям относятся также и дифференциальные связи, которые путем интегрирования могут быть приведены к соотношениям вида (1.2):

где — некоторые функции координат возможно, времени .

Если же дифференциальные связи вида (1.4) не могут быть путем интегрирования приведены к конечным соотношениям вида (1.2), то они называются

неголономными или неинтегрируемими. Г. Герц обратил внимание на важность различия между голономными и неголономными связями для понятия виртуального перемещения системы.

Легко видеть, что если голономные связи накладывают ограничения на возможные положения точек системы, то неголономные связи накладывают ограничения на скорости точек системы. Это следует из того, что уравнение неголономной связи (1.4) всегда может быть представлено в следующем виде:

Механические системы, подчиненные голономным связям, называются голономными системами. Если же в числе связей имеются неголономные, то системы называются неголономными.

Если на систему наложены только неголономные связи, то такая система называется сдвершенно неголономной или собственно неголономной.

Классическим примером движения неголономной системы может служить качение твердого шара по шероховатой плоскости (например, движение бильярдного шара).

Пусть твердый шар радиусом катится без скольжения по абсолютно шероховатой плоскости. Возьмем две системы координат с общим началом в центре шара С. Одна из них (система пусть движется поступательно, а вторая (система ) пусть будет жестко связана с шаром (рис. 1).

Положение шара в каждый момент времени может быть определено пятью координатами: двумя координатами центра шара (третья координата ) и тремя углами Эйлера: углом прецессии углом нутации 0 и углом собственного вращения (рис. 1). Условием связи в рассматриваемой задаче является условие касания шара с плоскостью и обращение

в нуль скорости точки А касания шара. Принимая центр шара С за полюс и обозначая его скорость через мгновенную угловую скорость вращения шара — через , а вектор-радиус, проведенный из центра шара в точку касания , — через , можем записать скорость точки А в следующем виде:

Проектируя это векторное равенство на оси координат и удовлетворяя условию связи получаем

где — составляющие вектора угловой скорости . Последнее уравнение интегрируется и дает одно уравнение связи показывающее, что центр шара С движется в плоскости, параллельной плоскости и отстоящей от нее на расстоянии, равном радиусу шара R.

Проекции угловой скорости на неподвижные оси выражаются, как известно, следующими формулами:

С помощью этих формул первые два уравнения связи (1.6) можно представить в следующем виде:

Эти два дифференциальных уравнения не могут быть приведены к конечным соотношениям путем интегрирования, и, следовательно, мы имеем здесь пример неголономной связи.

Посмотрим теперь, какой вид примут найденные уравнения связи (1.6) или, в развернутом виде, уравнения (1.8) в том случае, когда плоскость, по которой движется шар, будет абсолютно гладкая.

Рассматривая случай чистого скольжения, можем написать, что , следовательно,

Замечая, что получаем

Для интегрирования возведем оба уравнения в квадрат и сложим; тогда получим

Из этого соотношения следует

После интегрирования получаем

В рассматриваемом случае условие связи выражается равенством или т.е. связь голономна, и, следовательно, шар на абсолютно гладкой плоскости представляет собой пример голономной системы.

Примером неголономной связи может служить также случай качения и верчения диска с острыми краями по абсолютно шероховатой плоскости. Интересно отметить, однако, что плоскопараллельное движение диска — качение его по абсолютно шероховатой плоскости — дает пример голономной связи.

Действительно, в этом случае (рис. 2) условие связи имеет следующий вид:

Интегрируя, находим уравнения связи

а это означает, что связь будет голономной.

Из этого примера следует, что качение без скольжения цилиндра по абсолютно шероховатой плоскости также представляет случай голономной связи.

Читайте также: