Чему равна энергия контура в произвольный момент времени кратко

Обновлено: 06.07.2024

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

Соотношение (1) применяется при решении многих задач.

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1) :

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

Гармонический закон колебаний в контуре

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода

Сила тока считается положительной 0)' alt='(I > 0)' /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0' alt='I > 0' /> , то заряд левой пластины возрастает, и потому 0' alt='\dot > 0' /> .

Величины и меняются со временем, но энергия контура остаётся неизменной:

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):

Подставляя сюда и , получим:

Но сила тока не является функцией, тождественно равной нулю; поэтому

Перепишем это в виде:

Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

Амплитуда силы тока равна:

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

запишем закон изменения тока (13) в виде:

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .

Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

Для корректного отображения информации рекомендуем добавить наш сайт в исключения вашего блокировщика баннеров.

Для просмотра в натуральную величину нажмите на картинку

Идея нашего сайта - развиваться в направлении помощи ученикам школ и студентам. Мы размещаем задачи и решения к ним. Новые задачи, которые недавно добавляются на наш сайт, временно могут не содержать решения, но очень скоро решение появится, т.к. администраторы следят за этим. И если сегодня вы попали на наш сайт и не нашли решения, то завтра уже к этой задаче может появится решение, а также и ко многим другим задачам. основной поток посетителей к нам - это из поисковых систем при наборе запроса, содержащего условие задачи

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения \(U_=\dfrac\) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u \(\left(u = \dfrac \right).\) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e \(\left(W_=\dfrac>=\dfrac> \right),\) а сила тока в катушке i — энергию магнитного поля Wm \(\left(W_=\dfrac \right),\) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

В этом уроке мы вспомним, какие колебания называются электромагнитными. Узнаем, какие электромагнитные колебания являются гармоническими. Выясним, от чего зависит период свободных колебаний в идеальном колебательном контуре. А также узнаем, как связаны между собой амплитуды колебаний заряда и тока при разрядке конденсатора через катушку.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Идеальный колебательный контур. Формула Томсона"

На прошлом уроке мы с вами познакомились с электромагнитными колебаниями. Напомним, что так называют периодические изменения со временем электрических и магнитных величин в электрической цепи.

Рассмотрев качественную сторону теории процессов в колебательном контуре, перейдём к её количественной стороне. Для этого рассмотрим идеальный колебательный контур, то есть контур, активное сопротивление которого пренебрежимо мало.

В таком контуре, как мы показали ранее, полная электромагнитная энергия в любой момент времени равна сумме энергий электрического и магнитного полей, и она не меняется с течением времени:

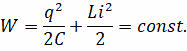
А раз энергия контура неизменная, то производная полной энергии по времени равна нулю:

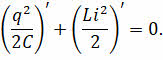
Напомним, что в записанной формуле заряд и сила тока в цепи являются функцией времени.

Чтобы понять физический смысл этого уравнения, перепишем его так:

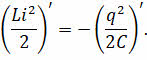
Из такой записи видно, что скорость изменения магнитного поля по модулю равна скорости изменения энергии электрического поля. А знак минус в формуле показывает на то, что увеличение энергии магнитного поля происходит за счёт убыли энергии поля электрического.

Вычислим производные в записанном уравнении, воспользовавшись для этого формулой вычисления производной сложной функции.

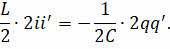
А теперь вспомним, что производная заряда по времени есть сила мгновенного тока (то есть сила тока в данный момент времени):

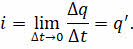
Поэтому предыдущее уравнение можно переписать так, как показано на экране:

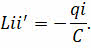
Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому, как производная скорости по времени (то есть ускорение) есть вторая производная координаты по времени:

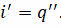
Перепишем предыдущее равенство с учётом этой поправки:

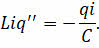
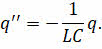
Данное уравнение аналогично уравнению, описывающему гармонические механические колебания:

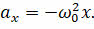
Отсюда видно, что величина, обратная квадратному корню из произведения индуктивности и ёмкости, является циклической частотой свободных электрических колебаний:

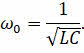
Зная циклическую частоту колебаний, нетрудно найти и их период, то есть минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется:

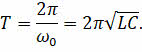
Эта формула впервые была получена английским физиком Уильямом Томсоном 1853 году, и в настоящее время носит его имя.

Из формулы видно, что период колебательного контура определяется параметрами составляющих его элементов: индуктивностью катушки и ёмкостью конденсатора. Из формулы Томсона также следует, что, например, при уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их частота — увеличиться и наоборот.

Но вернёмся к уравнению свободных электромагнитных колебаний в идеальном колебательном контуре. Его решением является уравнение, выражающее зависимость заряда конденсатора от времени:

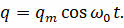
В записанной формуле q_m — это начальное (или амплитудное) значение заряда, сообщённому конденсатору. Из этой формулы следует, что заряд на конденсаторе изменяется со временем по гармоническому закону.

Если взять первую производную заряда конденсатора по времени, то мы получим уравнение, описывающее изменение силы тока в контуре:

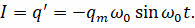
Величина, равная произведению максимального заряда конденсатора и циклической частоты колебаний, является амплитудным значением силы тока:

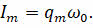
Перепишем уравнение для силы тока с учётом последнего равенства, а также воспользовавшись формулой приведения:

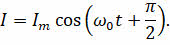
Из такой записи хорошо видно, что сила тока в колебательном контуре также совершает гармонические колебания с той же частотой, но по фазе она смещена на π/2 относительно колебаний заряда.

Для закрепления материала, решим с вами такую задачу. Конденсатор ёмкостью 2 мкФ зарядили до напряжения 100 В, а затем замкнули на катушку с индуктивностью 5 мГн. Определите заряд конденсатора через 0,025π мс после замыкания.

В заключение отметим, что в реальных колебательных контурах всегда имеется активное сопротивление, поэтому часть энергии контура всегда превращается во внутреннюю проводников, которая выделяется в виде излучения. Кроме того, часть энергии теряется на перемагничивание сердечника и изменение поляризации диэлектрика. Поэтому полная энергия контура с течением времени уменьшается, в результате уменьшается и амплитуда колебаний. Следовательно, реальные электромагнитные колебания в контуре являются затухающими.

Читайте также: