Зачем нужна алгебра логики в школе

Обновлено: 07.07.2024

Одна из приоритетных ценностей образования — интеллектуальное развитие ребенка, важной составляющей которого является развитие словесно-логического мышления.

Вложение	Размер
logika_v_shkolnom_matematicheskom_obrazovanii.doc	113 КБ

Предварительный просмотр:

Выполнила: Некрасова Наталья Михайловна

Одна из приоритетных ценностей образования — интеллектуальное развитие ребенка, важной составляющей которого является развитие словесно-логического мышления. Посему курс логики почти напрашивается в среднем образовании. Да так оно и было — одно время такой курс преподавался в советской школе, и мне довелось целый год выслушивать его. Было довольно скучно — вникать в понятия, суждения, умозаключения, оторванные от жизни, и, что еще более странно, не связанные с математикой (разве что приводились чисто математические примеры тому или иному положению из логики). Про обратные теоремы, необходимые и достаточные условия, метод доказательства от противного я узнал на уроках математики, а про всякого рода отношения между высказываниями (следование, равносильность) и математическую логику — вообще не в школе.

Когда курс логики убрали из нашего школьного образования, вся сложность проблемы перешла к математике, чему было несколько оснований.

Вот какова была позиция самих математиков. В.Феллер во введении к своему известному учебнику по теории вероятностей отмечал: «В каждой дисциплине мы должны заботиться о различении трех сторон теории:

а) формального логического содержания;

б) интуитивных представлений;

О важности развития логического мышления школьников писали такие известные математики, как А.Н.Колмогоров, Я.С.Дубнов, А.Я. Хин-чин, Б.В.Гнеденко, Л.А.Калужнин . Особая роль в этом отводилась геометрии, в которой его ценность выдающимися математиками — авторами школьных учебников считалась неотъемлемой и даже основной .

Развитие логического мышления всегда почиталось как одна из основных ценностей школьного математического образования и в педагогике математики, что нашло отражение, как в работах педагогического характера, так и в нормативных документах.

В связи с возникшей тенденцией — знакомить с логикой в курсе математики — в методической и учебной литературе появились многочисленные пособия по развитию логического мышления школьников. Эта тенденция отразилась и в учебниках математики, и в пособиях для поступающих в вузы. Более того, сегодня в школу возвращается сам курс логики — как элективный. На путях реализации этой тенденции необходимо сделать некоторые оговорки.

Логику можно воспринимать в трех аспектах.

Эти три логические ипостаси присутствуют в среднем образовании в том или ином виде, довольно хитро переплетаясь.

Пример 1. Недавно в одном из современных российских сериалов услышал следующий обмен репликами между двумя дамами (привожу почти дословно).

Пример 4. Много изречений такого рода содержится в сборниках законов Мерфи.

Мы видим, как смешиваются прямые утверждения и противоположные, обратные и им противоположные и пр. В литературном жанре это, видимо, приемлемо, но в житейской практике иногда хочется большей точности.

Еще один пример из того же источника.

Пример 5. А вот мои аналогичные вариации.

Всем детям полезны витамины. Всем взрослым полезны витамины. Второе предложение равносильно следующему: если кому-то не полезны
витамины, то это не взрослый, т.е. ребенок. А всем детям согласно первому предложению полезны витамины. И получается, что если кому-то
полезны витамины, то они ему же и не полезны. Что здесь не так?
Пример из математики. В выпуклом четырехугольнике сумма углов равна 360°. В невыпуклом четырехугольнике сумма углов равна 360°.
Отсюда, следуя той же схеме рассуждений, получим ляпсус.

Курс информатики только заостряет проблему. Как без использования основ математической логики объяснить ученикам компьютерную идеологию?

Проиллюстрирую возникающие трудности на примере построения отрицания. (В математике оно необходимо, в частности, при доказательстве от противного.) Проблемы перед учениками возникают даже тогда, когда требуется сформулировать отрицание в самых простых ситуациях, далеких от математики. Когда мы с чем-то не согласны, то считаем сказанное предложение неверным. Тогда какое предложение мы считаем верным? Его отрицание. И как его сформулировать?

Главный вопрос — где располагать частицу не и как от нее при необходимости избавиться?

Возьмем такие предложения:

Крокодилы живут в Африке;
Крокодилы не живут только в Гренландии.
Каково будет их отрицание?

Еще сложнее, когда предложение имеет форму конъюнкции, дизъюнкции или импликации. Вы увидите на лицах учеников отсвет недоумения, предложив им сформулировать верное отрицание, например, таких предложений.

Число 6 делится на 3 и число 5 делится на 3.
Число 5 делится на 3 или число 7 делится на 3.
Число 5 делится на 3 либо число 7 делится на 3. (Строгая дизъюнкция. — Прим. авт)
Если число 6 делится на 3, то число 5 делится на 3.
Данная фигура — квадрат или прямоугольник.
Данная фигура - прямоугольник и квадрат.
Данная фигура — квадрат либо прямоугольник.

Данная фигура — не квадрат и даже не прямоугольник.
Данная фигура — не только квадрат или прямоугольник.
Данная фигура — только не квадрат или прямоугольник.
Диагонали параллелограмма, пересекаясь, делятся точкой пересечения пополам.
Медианы треугольника, пересекаясь, делятся точкой пересечения в отношении 2:1, считая от вершины.

Если функция четная или нечетная, то ее график симметричен относительно начала координат и относительно оси ординат.
Если в четырехугольнике стороны равны, а диагонали взаимно перпендикулярны, то он является квадратом.

17)Два равновеликих треугольника равны, если они имеют пару соответственно равных сторон.

Ничего хуже защитник сказать не мог. Почему?

Уже простейшие примеры, связанные с построением отрицания предложения, показывают наличие определенных трудностей при освоении математики.

Но есть и более сложные, нежели отрицание, манипуляции с предложениями (обращение, контрапозиция), оценка их истинности, проверка равносильности и т.д. Все это очень непросто, и для формирования логической культуры почти необходима некоторая доля формализации. Естественно считать, что таковая обеспечивается начальными сведениями из формальной и математической логики.

Школьная математика — школа точного мышления, ее постижение начинается в 6—7 лет и длится непрерывно более десяти лет. Для точности мышления и понимания необходима точность языка. Точность естественного языка не всегда достаточна, слова и фразы не всегда толкуются однозначно, огромную роль играет контекст.

Еще хуже обстоят дела с квантором всеобщности, который, как уже отмечалось, опускают. Например, его нет в теореме о площади треугольника (площадь треугольника равна половине произведения его основания на высоту; а сколько таких оснований?) или в формуле квадрата суммы (о каких числах в ней говорится — о любых?).

Техника работы с кванторами позволяет упростить формулирование отрицания: можно уже не напрягать умственные способности, а работать чуть ли не механически. Вспомним определение последовательности, не имеющей предела, или функции, не являющейся периодической.

В работе с кванторами требуется соблюдать осторожность. Квантор всеобщности и квантор существования в предложении с двумя переменными нельзя произвольно менять местами (ученики довольно часто допускают такую ошибку).

Например, утверждать, что существует квадрат, который можно вписать в любой треугольник, — глупость. А сказать, что какой бы ни был треугольник, существует квадрат, который в него можно вписать, — значит фактически сформулировать задачу на построение.

Союзы и, или, если, если — то употребляются как в обычной, так и в математической речи. В естественном языке они придают множество смысловых оттенков отдельным словам или целым предложениям. В математике — трактуются необходимо однозначно. Отсюда — трудности в преподавании.

Я поведу сейчас речь о союзе если — то, о следовании предложений, об импликации, будь она неладна. Начну с последней.

Напомню, что импликация двух суждений имеет вид «если р, то р истинно, a q ложно, и истинна в остальных случаях.

Со времен древних греков не счесть работ по логике, в которых так или иначе не обсуждался бы этот феномен. Но и по сей день истинность импликации при ложной посылке подвергается сомнению. Даже предлагается в этом случае считать ее неопределенной или вовсе бессмысленной.

В обычной речи следование подразумевает наличие причинно-следственной связи (из того, что идет дождь, следует, что улицы мокрые), логической связи (из того, что Сократ — человек, следует, что он смертен, ибо все люди смертны), содержательной связи (следствия из формул). Тем самым на практике из ложного условия не может следовать верное предложение.

Приведу примеры того, как путаница в терминологии и обозначениях сказывается на решении уравнений, неравенств, систем (дальше я для краткости буду говорить только об уравнениях. — Прим. авт.), если трактовать их как предикаты.

При решении уравнений авторы многих пособий при переходе от имеющегося уравнения к следующему как выводному (неравносильному) говорят, что второе уравнение есть следствие первого, и ставят знак =>.

По существу происходит отказ от импликации предикатов, речь идет об их следовании, по сути — об отношении включения между двумя множествами. Однако при решении уравнения не исключен случай отсутствия корней. Я вижу здесь некое противоречие: из ложной посылки не бывает следствий, однако пустое множество включено в любое множество. Так что, в этом случае возвращаться к толкованию процесса решения уравнения как к импликации предикатов?

х = 2, нежели в виде или х . Запись ответа в виде множества, разумеется, возможна. Однако она менее естественна и чревата сложностями, особенно когда речь идет об ответе тригонометрического уравнения.

Тут же уместно сказать об употреблении логической символики; это стало достаточно привычным, но, увы, иногда делается неряшливо.

Ученикам надо объяснить, что знаки символической логики - это не знаки стенографии и в серьезной работе как таковые недопустимы (учащиеся особенно любят использовать в таком качестве кванторы).

Второй момент, когда приходится обсуждать с учениками расхождение формального и содержательного, возникает при встрече с задачей, условие которой противоречиво.

Сталкиваться с противоречиями приходится и в жизни. На основе противоречивых данных порой принимаются важные решения (юристами, медиками, разведчиками), но никто не скажет, что такие решения следуют (логически) из этих данных.

В школьном курсе математики задач с противоречивыми данными по традиции нет, условие всегда достоверно. Полезно, однако, научить школьника видеть противоречие в полученной информации и осмыслять его (по утверждениям психологов, чувствительность к противоречию — один из параметров интеллекта). При этом я полагаю, что ответ типа

Приведу несколько примеров.

И что же должен делать учитель, предложивший ученикам задачу с противоречивым условием? Считать полученный ответ верным (согласно толкованию задачи как импликации в формальной логике) или зафиксировать ошибку, коль скоро ученик не обнаружил противоречия, и считать его ответ неверным?

Полагаю, что важно приучать школьников к анализу условия на непротиворечивость, и, если противоречие будет обнаружено, пусть ученик в ответе напишет примерно так: поскольку условие задачи противоречиво, ответить на поставленный вопрос невозможно. Задача не всегда имеет чисто формальный характер.

В теореме, в каждом математическом предложении есть содержание и форма. Суть теоремы, задачи заключается в ее содержании.

Предмет логика был введен в учебных заведениях еще во времена Российской Империи. С приходом советской власти предмет был упразднен в силу невозможности преподавания марксистских позиций.

После Великой Отечественной войны логика вновь стала преподаваться в школах. Учителя математики стали внедрять ее на своем предмете.

С приходом к власти Хрущева преподавание логики было полностью свернуто как в школах, так и в высших учебных заведениях. Считалось, что логика не может разрешить спорные ситуации, а на это способен лишь диалектический материализм.

Данную информацию я почерпнул из Интернета, так как в те годы я не жил.

А что такое логика? Как говорят в словаре, логика это наука здравомыслия. А что такое здравомыслие? Это очень опасное слово.

Почему в современной российской школе нет предмета "логика"? Отчасти логика изучается, формально присутствует в некоторых школьных предметах, например, в информатике.

Но тут немного другая область. Та логика, которой учили в Имперской России и некоторое время в СССР, действительно была разработанным школьным предметом, который можно было не только вести, но и научить этой самой логике.

А нужно ли в современной школе преподавание логики?

Вот тут небольшой опрос . После голосования сразу доступны результаты.

Конечно, отсутствие предмета "логика" не означает, что школьники не овладевают элементарными умениями "здраво мыслить". У кого-то это заложено изначально, а кто-то приобретает со временем. Но далеко не все.

Вполне возможно, что введение предмета могло бы действительно принести пользу на раннем этапе развития ребенка. Но вот только введение данного предмета в российской школе было бы малоэффективным.

- нет специалистов. "Проходить переподготовку" было бы поручено учителям, которые "смеют отказать". А "переподготовка

- изначально не будет достойных учебников. Я уже много раз убеждался, что школьные учебники это сегодня отличный бизнес. За качество наполнения никто не отвечает.

- невозможно введение логики методом вклинивания в расписание, увеличивая и без того громадную нагрузку на школьников.

- эффект упущенного времени. Только лишь следующее поколение поймет, зачем в школах был нужен предмет "логика".

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

* Программа предусматривает обучение в объеме 68 часов в течении 2-х лет (10 – 11 класс) Курс носит интегративный, междисциплинарный характер.

* Важность и актуальность алгебры логики можно рассматривать в трех аспектах: Одно из приложений логики состоит в использовании ее методов для проведения и проверки рассуждений. При решении логических задач ученикам предоставляется возможность подумать над условием, рассуждать, сконструировать логически обоснованное решение задачи, что является лучшим способом раскрытия творческих способностей учеников. Таким образом, изучение данного раздела позволяет учащимся более качественно овладеть знаниями по другим учебным предметам, а это доказывает интегрирующую роль информатики в целом и данного курса в частности. Овладевший приемами логического мышления всегда понятен в разговоре, исключает всякую бессистемность в обработке информации. Он умеет находить рациональное зерно в чужой сбивчивой речи, оценивать доказательную силу высказываний в дискуссии, находить кратчайшие и правильные пути исправления ошибок. Важную роль играет изучение элементов алгебры логики в курсе информатики, так как её аппарат используется во многих содержательных линиях. Знание алгебры логики необходимо учащимся при сдаче ЕГЭ.

* Психолого-педагогическое обоснование Учет возрастных особенностей – один из основополагающих педагогических принципов. Они обуславливают выбор форм и методов учебно-воспитательной деятельности. Юношеский возраст (15 – 18 лет) – это период выработки мировоззрения, убеждения, характера и жизненного самоопределения. Старшеклассники существенно отличаются друг от друга не только по темпераменту и по характеру, но и по своим способностям, потребностям, стремлениям и интересам, разной степенью самосознания. Индивидуальные особенности проявляются и в выборе жизненного пути. Жизненные планы, ценностные ориентации старших школьников отличаются резкой дифференциацией по интересам и намерениям К этому возрасту у обучающихся развиваются качества: ПСИХОЛОГИЧЕСКИЕ Аналитико-синтетическое восприятие, наблюдательность, регулируемая память, абстрактное мышление, целесообразование и планирование, способность рассуждать, интеллектуальная познавательная активность; креативность; чувство психологической защищенности, учебно-познавательные интересы, мотивация достижения успеха, социальная мотивация (долг, ответственность); уверенность в себе, усидчивость, самостоятельность в действиях, желание и способность иметь собственное мнение, коммуникабельность. ЛИЧНОСТНЫЕ Социальная взрослость, ответственность за свои действия, мотивация общественно полезной деятельности (учебно-трудовой и т.д.), познавательные интересы, самосознание и адекватная самооценка, потребность в самопознании, осознание собственной индивидуальности, личностное самоопределение, стремление к самоутверждению, потребность в общественном признании, удовлетворенность своим положением, нравственное осознание.

* Анализ моей педагогической деятельности в 10-11-х классах, показывает, что обучающиеся, в основном, способны освоить учебный материал на достаточно высоком уровне трудности. Обучающиеся смотивированы на учебно-позновательную деятельность. Осмысленно воспринимают учебный материал. При составлении планов уроков я также учитываю известные из психолого-педагогической литературы факты: забывание более интенсивно протекает сразу после изучения материала (в первый день, в первые часы и даже минуты), затем оно замедляется; 2) повторение путем разнообразной деятельности, сводящейся хотя бы к некоторой реконструкции материала, эффективнее, чем его повторение в неизменном виде; 3) рассредоточенное по времени повторение эффективнее, чем концентрированное.

* ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ. Учащиеся осваивают представления о современных информационных технологиях, осваивают навыки работы с компьютером, применяют ПК для решения задач, повышают информационную культуру; ЛИЧНОСТНО-ОРИЕНТИРОВАННЫЕ ТЕХНОЛОГИИ. Целостная включенность в образовательный процесс возможна только при эмоциональной реакции учащихся. Ученик – это личность. Формирование индивидуального образовательного маршрута реализуется через дифференцированное и эвристическое обучение, в основе которых лежит идея самореализации личностного потенциала каждого обучающегося. ИГРОВЫЕ ТЕХНОЛОГИИ. Реализуются через игровые ситуации, которые выступают как средство побуждения, стимулирования учащихся к учебной деятельности. Особенно они эффективны при решении текстовых логических задач

* Методы и формы словесные методы обучения (рассказ, объяснение, лекция, беседа, работа с учебником); наглядные методы ( иллюстрация, видеоуроки, презентации); практические методы (устные и письменные упражнения, практические работы за ПК); активные методы (метод проблемных ситуаций, дискуссии, метод проектов, эвристическая беседа). Формы работы: фронтальная, групповая, коллективная, парная, индивидуальная.

* Приёмы Приемы общей (внешней) организации учебной деятельности – приемы слушания, наблюдения, планирования работы с учебником, компьютером и другими средствами информации, пересказа информации, самоконтроля, организации учебного общения, организации домашней работы и т.п.; приемы познавательной (внутренней) деятельности – приемы развития внимания, приемы запоминания, оперирования образами, представлениями, понятиями, суждениями, умозаключениями, мыслительными операциями и действиями, приемами словесного описания, объяснения, формулировки вопросов или проблем, приемы рефлексии и др.; Отличительная черта курса информатики – активное и систематическое использование в учебном процессе средств ИКТ (в том числе и домашнего ПК), эффективность применения которых в значительной степени зависит от правильного выбора приемов их использования (применение заготовок, облегчающих рутинную работу, электронных пособий и учебников, электронной почты и т.д.)

* СИСТЕМА ДЕЯТЕЛЬНОСТИ Познавательнаяреализуются мыслительные операции: анализ, синтез, абстрагирование, обобщение; постановка проблемы, установление причинно-следственных связей, применение методов дедукции и индукции; Преобразующая действия в ситуациях неопределенности; техника выбора; поиск путей решения проблем. Общеучебная организация рабочего места; работа с учебником, интерактивным тестом, конспектом; развитие навыков общения. Самооргани- зующая планирование деятельности; самоконтроль, самооценка; рефлексия, осознание своего продвижения.

* Цели и задачи Цель: ввести основные понятия алгебры логики, показать применение изложенной теории на практике. задачи: научить учащихся понимать смысл терминов алгебры логики; изучить способы решения логических задач; показать взаимовлияние математики и информатики; Цель: развить мыслительные умения и способности каждого ученика. задачи: развить логическое мышление; развить умения синтезировать, анализировать, обобщать; развить эвристический стиль мышления; развить познавательный интерес. Цель: воспитать творческую личность, готовую свои познавательные возможности использовать в жизненных ситуациях задачи: воспитать культуру мышления; воспитать трудолюбие, дисциплинированность; Воспитать навыки сотрудничества и коллективного взаимодействия; показать социальную значимость алгебры логики.

* В результате обучения учащиеся должны: знать: что такое логическая величина, логические операции, как они выполняются, логическая функция, таблица истинности, структурная схема, СКНФ и СДНФ; уметь: записывать логическую функцию различными способами, составлять таблицы истинности, составлять структурные схемы по заданным формулам и таблицам истинности, решать логические содержательные задачи различными способами; использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для развития логического мышления, интеллекта, успешной сдачи экзамена по информатике, сотрудничества и коллективного взаимодействия.

Пояснительная записка Предварительная информация об уроке: 5-й урок по счету, завершающий урок перед самостоятельной работой; К данному уроку учащиеся владеют необходимыми знаниями и умениями: умеют выделять и формализовать высказывания, знают основные логические операции и законы логики, умеют строить таблицы истинности для сложных логических выражений, в том числе и с применением электронных таблиц Excel; Знают табличный, графический способы решения логических задач и путем рассуждений (из курса 5,6 класса); Тема урока и вопросы для повторения к уроку сообщены учащимся заранее.

Актуальность урока состоит в следующем: Решение логических задач способствует развитию очень важного умения – формализации задач; Урок показывает применение алгебры логики на практике; Решение логических задач позволяет закрепить использование математического аппарата алгебры логики; Решение логических задач вызывает у учащихся как интерес, так и определенные трудности; Аппарат алгебры логики позволяет построить формальный универсальный способ решения логических задач; Текстовые логические задачи есть в заданиях ЕГЭ.

* Цели и задачи урока

План урока: Тип урока – комбинированный, поэтому в нем присутствуют следующие этапы: Организационный этап: Организационный момент, Постановка цели и задач урока, Описание методов организации работы учащихся на уроке. 2. Проверка знаний: проверка домашнего задания, разминка, подготовка учащихся к восприятию материала на основном этапе урока, тестирование учащихся. 3. Актуализация знаний: постановка проблемы, выбор путей решения проблемы, 4. Усвоение новых знаний: Решение текстовой логической задачи с использованием алгебры логики, Проверка результата с помощью электронных таблиц. 5. Первичное закрепление новых знаний: Решение логических задач табличным способом, Решение логических задач с использованием законов алгебры логики. 6. Информация о домашнем задании 7. Подведение итогов. Рефлексия.

* Этап урокавремяДеятельность учителяДеятельность учащихся 7. Подведение итогов. Рефлексия.2 минПредлагает учащимся сформулировать способы решения логических задач, записать их в тетрадь. Есть ли универсальный способ? Когда целесообразно его применять? Оценивает деятельность учащихся на уроке, выставляет оценки. Предлагает учащимся оценить свою деятельность на уроке (слайд 14) Отвечают на вопросы, делают выводы и записи в тетради. Оценивают свою деятельность на уроке.

* Используемые источники: Е.В.Андреева, Л.Л.Босова., И.Н.Фалина, Математические основы информатики: Учебное пособие, М., БИНОМ, Лаборатория знаний, 2007 Е.В.Андреева, Л.Л.Босова., И.Н.Фалина, Математические основы информатики: Методическое пособие, М., БИНОМ, Лаборатория знаний, 2007 Программы для общеобразовательных учреждений 2-11 классы (составитель М.Н.Бородин): М., БИНОМ, Лаборатория знаний, 2008

Элементы математической логики всё больше проникают в школьное образование: это и математика (логические истинности), и информатика (понятия и законы математической логики, умения строить таблицы истинности и логические схемы, умения строить и преобразовывать логические выражения). Элементы логики, стали “обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение”.

Особое место занимает понятие логически истинного предложения (логическая истина), оно является центральным логическим понятием, представляя логику в рассуждениях и доказательствах.

В статье я сделаю попытку показать, как можно ввести понятие “логическая истина” в жизнь обычного школьника.

Перед Вами изложение теоретического материала для учащихся (текст выдаётся каждому школьнику, который добровольно пришёл на математический семинар). Как правило, длительность семинара от 45 минут (1 занятие) до 225 (5 занятий). Темы и время проведения семинаров объявляются в начале учебного периода: четверти, полугодия. В семинаре участвуют, как минимум 6 учеников, как максимум 20, всё зависит от заявленной темы. Участники – ребята разных классов: в 2010/2011 – 9, 10, 11 классы, в 2011/2012 году – 6, 8 классы, в 2012/2013 – 7, 9.

Тема. Логические истины. (225 минут)

Очевидно, что каждая наука имеет свой словарь. Например, в биологическом словаре: анабиоз, бактериофаг, гаметы, ген, клетка, селекция, штамм; в музыкальном словаре: бард, двойной хор, запев, звукоряд, фальцет; в физическом словаре: масса, путь, скорость; в химическом – молекула, моль, реакция; в математическом – многоугольник, число, уравнение, функция.

Выясним, какие слова входят в словарь математической логики, а также что такое логическая истина. Рассмотрим известное предложение: “Если все люди смертны ()и все герои – люди (), то все герои смертны ()”. Ясно, что это предложение истинное. Заменим в этом предложении слова “люди”, “смертны” и “герои” соответственно словами “животные”, “дышат”, “киты”. Получим новое предложение: “Если все животные дышат и все киты – животные, то все киты дышат”, которое также истинное. Таких замен можно привести достаточно много. Приведённые предложения имеют различные сюжеты (содержание или смысл), однако, их истинность не нарушилась от замены содержания.

Очистим рассматриваемые предложения от их содержания, и получим форму:

“Если все *₁, *₂ и все *₃ есть *₁ все *₃ *₂” Подставив в полученную форму одни и те же слова вместо одинаково пронумерованных звёздочек, всегда получим истинные предложения. Итак, предложения, истинность которых зависит только от формы и не зависит от содержания, называются логически истинными предложениями (логическими истинами).

Я сдам или не сдам зачёт по математике.
Из того, что если я отдыхаю, то я сплю, следует, что если я не сплю, то я не отдыхаю.
Электрическое напряжение в сети есть или его нет.
Если существует х такое, что 5 – х = 0, то не для всех х не имеет места 5 – х = 0.

Слова, из которых строится форма предложения, составляют логический словарь.

Это – “и”, “или”, “не”, “если…, то…”, “тогда и только тогда”, “все”, “существует”, “некоторые”, “никакой” и т.д.

Изучение логических истин – основная задача логики, вернее одна из основных задач. Однако, критерий истинности в логике не такой, как в естественных науках. В естественных науках важна не форма, а содержание. Подтверждение истинности в естественных науках требует проведение эксперимента, наблюдений. В логике критерий истинности во многом определяется синтаксической структурой (формой) предложения.

При аксиоматическом построении математики (в частности геометрии) теорему мы рассматриваем как некое условное предложение, логическую истинность которого доказываем.

Рассмотрим основные понятия и символику математической логики.

По аналогии – двуместный предикат с областью значений (х; у) где и х и у – действительные числа. (1; -6) превращает предикат в истинное высказывание, (1; 6) – ложное.

В логике принято однозначно определять истинность сложного высказывания через истинность высказываний его составляющих, пользуясь следующими договоренностями.

Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание. Суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита. Истинному высказыванию соответствует значение логической переменной 1, а ложному – 0.

Несколько советов учителю, которому интересна идея введения элементов логики в школе (элективный курс, семинар для желающих учеников, . ).

По моему мнению, логическая подготовка школьников может быть разделена на три этапа.

1. Подготовительный этап

Необходимо учить школьников (начинать можно уже в начальной школе) понимать логическую структуру предложений и правильно применять слова и словосочетания, такие как: “и”, “или”, “не”, “хотя бы…”, “если…, то…”, “необходимо”, “достаточно”, “необходимо и достаточно”, “все”, “некоторые” и др. Постепенно приучать находить истинность или ложность сложных предложений в зависимости от их логического строения и истинностных значений, составляющих их предложений. Ученик должен твёрдо усвоить, что запись – истинное высказывание, потому что это сложное высказывание “ или 2 > 2“, которое истинно, если…

Особое внимание необходимо уделить выработке навыка правильного понимания условных предложений. Он должен без колебаний относить предложения “Если , то 1 = 1”, “Если 0 = 1, то 1 = 2” к истинным высказываниям. Думаю, что в разумных пределах, необходимо учить школьников пользоваться логической символикой.

2. Формирование понятия о логическом законе

Идею логического закона следует формировать постепенно, не стремясь к формальным и строгим определениям. Необходимо в начале научить выделять логические истины, делая акцент на их отличии от не логических, фактических истин, учить замечать общую форму логических истин, прибегая к символике, доказывать простые логические законы и опровергать ошибочные гипотезы о логической истинности предложений.

3. Выработка навыков использования логических законов в рассуждениях.

Без четкого понимания логических связей, логических законов, отношений следования и эквивалентности ученики способны лишь заучить доказательство, оказываются беспомощными в попытках самостоятельно его отыскать.

Одна из центральных задач обучения математике состоит в обучении установлению истинности математических предложений (чаще всего с помощью доказательства), а истинностные значения этих предложений зависят от их логической структуры, то естественно считать одной из главных задач обучения математике раскрытие логической структуры математических предложений.

Каждая математическая теория представляет собой множество предложений, описывающее какую-то структуру (если эта теория излагается содержательно в определенной конкретной интерпретации, как это имеет место в школьном обучении).

предложение записано (или сформулировано) на языке данной теории, состоит из математических (принадлежащих языку теории) и логических терминов или символов и не содержит никаких других терминов или символов;
предложение истинно, т. е. является или исходным истинным предложением (аксиомой) данной теории, или его истинность устанавливается доказательством с помощью уже известных (исходных или ранее доказанных) истинных предложений.

Например, предложение “Вертикальные углы равны” является геометрическим предложением, принадлежит теории евклидовой геометрии, потому что: оно записано на языке геометрии (и одновременно па русском языке), т. е. состоит из геометрических (“вертикальные углы”) и логических (“равны”) терминов или символов; оно истинно, так как доказывается в рамках евклидовой геометрии, т. е. на основе ее аксиом или других уже доказанных предложений этой теории.

С каждым математическим предложением связаны содержание (выраженное в нем математическое содержание) и логическая форма (или структура).

Представление, что можно ограничиться в обучении математике лишь раскрытием содержания каждого математического предложения, ошибочно. Содержание неразрывно связано с формой, и нельзя осмыслить первое без понимания второй.

Раскрыть логическую структуру сложного (составного) предложения – значит показать, из каких элементарных предложений сконструировано данное сложное предложение и как оно составлено из них, т. е. с помощью каких и в каком порядке применяемых логических связок (слов или сочетаний слов) “не”, “и”, “или” , “если. то” , “тогда и только тогда” , “для всякого” , “существует” (и некоторых синонимических выражений), обозначающих логические операции, с помощью которых из одних предложений образуются другие.

Всякое математическое (и не только математическое) предложение либо элементарное, (не расчленяется на части, каждая из которых в свою очередь есть предложение), либо построено из элементарных, определенным образом соединенных между собой логическими связками.

Логическую структуру любого сложного предложения необходимо раскрывать с обязательным разъяснением точного смысла применяемых логических связок.

Такое разъяснение необходимо потому, что, применение, даже многократное, перечисленных выше слов само по себе еще не обеспечивает правильного понимания их смысла. Не только школьники, но и некоторые взрослые, много тысяч раз применявшие в своих рассуждениях союз “или”, отвечают отрицательно, например, на вопрос: «Истинно ли предложение ’’4 13.07.2013

Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.

Что такое алгебра и алгебра логики

Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.

Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.

Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.

Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.

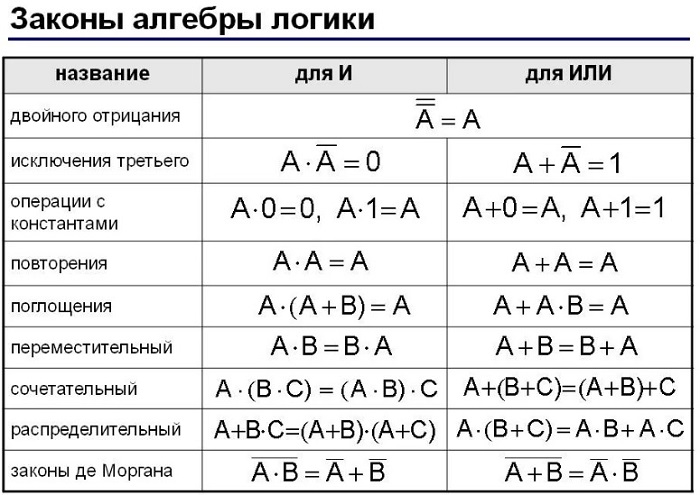
Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.

Основные законы алгебры логики представлены в таблице:

Логические выражения

В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.

Нью-Йорк — столица США (ложное);

в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.

Идёт дождь, а у меня нет зонта.

Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

Логическое отрицание (инверсия) —НЕ

Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).

Таблица истинности инверсии:

Результаты операции НЕ следующие:

если исходное выражение истинно, то результат его отрицания будет ложным;

если исходное выражение ложно, то результат его отрицания будет истинным.

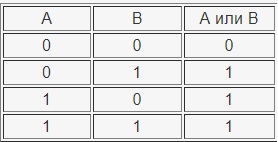
Логическое сложение (дизъюнкция, объединение) — ИЛИ

Таблица истинности операции ИЛИ:

Логическое умножение(конъюнкция) — И

В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).

При всех остальных значениях операция будет ложной.

Таблица истинности операции И приведена ниже:

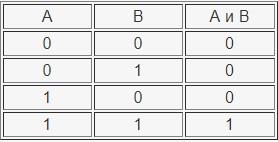
Логическое следование (импликация) — ЕСЛИ ТО

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.

Таблица истинности операции ЕСЛИ ТО выглядит так:

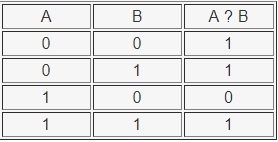
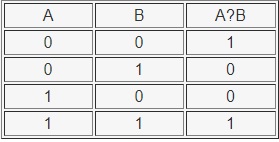
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В

Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

Таблица истинности операции эквивалентности:

Читайте также: