В школе четыре выпускных класса сколько способов распределения экзаменаторов

Обновлено: 05.07.2024

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье – n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m ( ) из этих (n*r) предметов?

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

1. Школа предлагает сдавать 12 экзаменов по различным предметам. Сколькими способами ученик может выбрать экзамены, которые будет сдавать, если всего надо сдать 5 экзаменов, при этом сочинение и алгебру надо сдавать всем? (120 или как предлагают в ответе - 165?)

2. Вокруг круглого стола надо посадить шесть человек. Сколькими видами это можно сделать? (720 или как предлагают в ответе - 120?)

3. Сколькими способами 7 друзей могут сесть вокруг круглого стола, если Ваня и Гриша не хотят сидеть рядом друг с другом?

1. У меня получается 120. Т. е. 2 экзамена известно, остается выбрать 3 из 10.
Число сочетаний из 10 по 3 равно 10!/(7!*3!)=10*9*8/(2*3)=120
2. Если считать, что позиция 1-го за круглым столом не важна, то задача сводится как рассадить остальных.
Для второго осталось 5 вариантов, для третьего -4 и т. д. , т. е 5!=5*4*3*2*1=120
3. Задача в 2 этапа. Сначала не обращаем внимание на Ваню и Гришу. По аналогии с предыдущей это 6! = 720 вариантов
Теперь посмотрим, сколько вариантов, что Ваня и Гриша сидят вместе. Т. е. это предыдущая задача полностью (Ваню и Гришу считаем за слитную пару) , значит это 120 вариантов.
Вычитаем 720-120=600 вариантов

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Задачи для решения на закрепление нового материала

Задача № 1 . Сколькими способами могут быть расставлены 5 участниц финального

забега на 5-ти беговых дорожках?

Решение : Р ₅ = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая

цифра входит в изображение числа только один раз?

Решение : Число всех перестановок из трех элементов равно Р ₃ =3!, где 3!=1 * 2 * 3=6

Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести

девушек на танец?

Решение : два юноши не могут одновременно пригласить одну и ту же девушку. И

варианты, при которых одни и те же девушки танцуют с разными юношами,

считаются разными, поэтому:

Задача № 4 . Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,

6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только

Решение : В условии задачи предложено подсчитать число всевозможных комбинаций из

трех цифр, взятых из предположенных девяти цифр, причём порядок

расположения цифр в комбинации имеет значение (например, числа 132)

и 231 различные). Иначе говоря, нужно найти число размещений из девяти

элементов по три.

По формуле числа размещений находим:

Ответ : 504 трехзначных чисел.

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3

Решение: Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все

возможные 3 – элементные подмножества множества, состоящего из 7

человек. Искомое число способов равно

Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов

распределения призовых (1, 2, 3) мест?

Решение : А ₁₂ 3 = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест. Ответ : 1320 вариантов.

Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из

10 спортсменов. Сколькими способами тренер может определить, кто из них

побежит в эстафете 4  100 м на первом, втором, третьем и четвёртом этапах?

Решение: Выбор из 10 по 4 с учётом порядка: способов.

Ответ: 5040 способов.

Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

второе – любой из трех оставшихся (3 способа), на третье место – любой из

оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

Всего 4 · 3 · 2 · 1 = 24 способа.

Р ₄ = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.

Задача № 9 . Учащимся дали список из 10 книг, которые рекомендуется прочитать во

время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: способов.

Ответ: 210 способов.

Задача № 10 . В 9 классе учатся 7 учащихся, в 10 - 9 учащихся, а в 11 - 8 учащихся. Для

работы на пришкольном участке надо выделить двух учащихся из 9 класса,

трех – из 10, и одного – из 11 . Сколько существует способов выбора

учащихся для работы на пришкольном участке?

Решение: Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из

первой совокупности (С ₇ 2 ) может сочетаться с каждым вариантом выбора из

второй (С ₉ 3 ) ) и с каждым вариантом выбора третьей (С ₈ 1 ) по правилу

Ответ: 14 112 способов.

Задача № 11. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на

перемене к теннисному столу, за которым уже шла игра. Сколькими

способами подбежавшие к столу пятеро девятиклассников могут занять

очередь для игры в настольный теннис?

Решение : Первым в очередь мог встать любой девятиклассник, вторым – любой из

оставшихся троих, третьим – любой из оставшихся двоих и четвёртым –

девятиклассник, подбежавший предпоследним, а пятым – последний. По

правилу умножения у пяти учащихся существует 5· 4  3  2  1=120 способов

подготовка к ЕГЭ/ОГЭ и ВПР
по всем предметам 1-11 классов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

ЗП до 91 000 руб.
Гибкий график
Удаленная работа

Дистанционные курсы для педагогов

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 590 946 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

25.09.2016 49683
DOCX 52 кбайт
442 скачивания
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Волошина Елена Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

40%

Подготовка к ЕГЭ/ОГЭ и ВПР
Для учеников 1-11 классов

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Время чтения: 1 минута

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Число всех сочетаний из n элементов по k обозначается символом и вычисляется по формуле:

(4)

В частности, что согласуется с тем, что у любого множества Х имеется только одно подмножество из нуля элементов ( пустое подмножество ), и только одно подмножество из n элементов (совпадающее с самим множеством X ).

При рассмотрении сочетаний очень мощно используется теория множеств!

Докажем формулу (4).

Пусть Y какое-либо произвольное подмножество множества Х , содержащее k элементов (то есть сочетание из n элементов по k ). Число таких подмножеств обозначим символом . Необходимо выяснить, чему равно это число.

Составляя, всевозможные перестановки из элементов этого множества Y получим k ! различных строк длиной k . Если указанную операцию проделать с каждым подмножеством Y содержащим k элементов, то получим всего различных строк, длиной k . С другой стороны, таким образом должны получиться все без исключения строки, длиной k без повторений, которые можно составить из элементов множества Х . Число таких строк равно , следовательно, . Выражая из этого равенства , получим:

. Формула (4) доказана.

Числа называют биномиальными коэффициентами – они входят в формулу бинома Ньютона, изучение которого также входит в программу по математике для профильных классов.

Числа обладают рядом замечательных свойств:

1. (доказывается непосредственно по формуле (4));

2. (можно доказать с помощью известной теоремы из теории множеств о том, что число различных подмножеств n - элементного множества равно 2 n ; другой способ доказательства - комбинаторный);

3. для любых (доказывается с помощью формулы (4)); на основе этого свойства строится знаменитый треугольник Паскаля.

Таблица 1.Треугольник Паскаля

Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице 1, арифметическим . Паскаль посвятил свойствам арифметического треугольника основополагающий "Трактат об арифметическом треугольнике" (1654). Справедливости ради, стоит упомянуть, что биномиальные коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник Паскаля называют треугольником Тартальи.

Пример. Во взводе 5 сержантов и 50 солдат. Сколькими способами можно составить наряд из одного сержанта и трёх солдат.

Решение. Одного сержанта из пяти можно выбрать 5-ю разными способами. Для любого из этих способов выбора сержанта трёх солдат (порядок тройки не важен) из 50-ти можно выбрать числом способов. Тогда по правилу произведения весь наряд, то есть одного сержанта и трёх солдат, можно выбрать способами.

Подобные задачи очень часто встречаются в комбинаторике и в теории вероятностей. Поэтому рассмотрим модель этой задачи и её решение.

Пусть имеется n объектов I типа и m объектов II типа. Сколькими способами можно выбрать из них k объектов I типа и s объектов II типа?

Условие задачи рекомендуется оформить таблицей, чтобы не запутаться в числах при составлении числа сочетаний.

объектов

Тогда объектов I типа из можно выбрать числом способов. Для каждого из этих способов выбора объектов I типа объектов II типа из имеющихся можно выбрать числом способов. Применяя правило произведения, получаем ответ:.

Аналогично решается задача для объектов трёх, четырёх и т.д. типов.

К подобной задаче сводятся задачи, в которых известно общее количество имеющихся объектов и общее количество тех, которые нужно выбрать.

Пример. В классе 36 человек, из которых 6 – отличники. Сколькими способами можно разбить класс на два класса по 18 человек так, чтобы отличников в каждом классе было поровну?

Решение. Разбить класс на две части по 18 человек – это всё равно, что выбрать 18 человек из 36. Отобранные 18 человек составляют один класс, оставшиеся – другой. Оформим условие задачи в указанном выше виде.

I тип - отличники

Есть 36 человек:

27 не отличников

15 не отличников

Ответ: способов.

1. Ф. У лесника 3 собаки: Астра (А), Вега (В) и Гриф (Г). На охоту лесник решил пойти с двумя собаками. Перечислить все варианты выбора лесником пары собак.

Это задача о выборе двух элементов из трех без учета порядка. Перечислим варианты выбора из А, Б, В по два: А, Б; А, В; Б, В. Если учащиеся знают формулу для числа сочетаний, то количество вариантов равно: =3.

Ответ: 3 варианта.

2. Ф. Сколько существует способов выбрать троих ребят из четверых желающих дежурить по столовой?

Количество сочетаний из 4 по 3 (порядок выбора не имеет значения) равно: = 4. Иначе можно рассуждать так. Вместо выбора троих дежурных выберем одного, который не будет дежурить, а трех оставшихся отправим на дежурство. Количество способов выбрать одного из четверых ребят равно 4.

Ответ: 4 способа.

М-задачи из уч. пособия А.Г.Мордковича

Т- под ред. С.А.Теляковского

3. Т. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Выбираем 2 учащихся из 7, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 7 по 2: способ.

Ответ: 21 способ.

Выбор из 8 по 3 без учета порядка: = 56 способов.

Ответ: 56 способов.

5. Т. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Выбор 6 из 10 без учета порядка: способов.

Ответ: 210 способов.

а) заведующий лабораторией должен ехать в командировку;

б) заведующий лабораторией должен остаться?

Из 11 человек 5 должны поехать в командировку.

а) Заведующий едет, нужно выбрать еще 4 из 10 оставшихся:способов.

в) Заведующий остается, нужно выбрать 5 из 10 сотрудников: способа.

Ответ: а) 210 способов; б) 252 способа.

7. Т. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими cnocoбами он может выбрать из них 3 книги и 2 журнала?

Нужно сделать два выбора: 3 книги из 10 ( способов) и 2 журнала из 4 ( способов) ; порядок выбора не имеет значения. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно: способов.

Ответ: 720 способов.

а) Иванов и Петров должны пойти в наряд обязательно;

б) Иванов и Петров должны остаться;

в) Иванов должен пойти в наряд, а Петров – остаться?

Выбираем три элемента из 12; порядок выбора не имеет значения (все трое идут в наряд).

а) Иванов и Петров идут в наряд, еще одного нужно выбрать из других 10 солдат; количество способов: С= 10.

б) Иванов и Петров не идут в наряд; троих идущих в наряд нужно выбрать из других 10 солдат; количество способов: способов.

в) Иванов идет в наряд, а Петров остается. Еще двоих, идущих в наряд с Ивановым, нужно выбрать из других 10 солдат ( Иванова и Петрова не считаем); количество способов:

Ответ: а) 10способов; б) 120 способов; в) 45 способов.

9. Т. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?

Нужно сделать два выбора: 4 мальчиков из 16 ( всего способов); порядок выбора значения не имеет ( все идущие на уборку равноправны). Каждый вариант выбора мальчиков может сочетаться с каждым выбором девочек,

Поэтому по правилу произведения общее число способов выбора равно:

способов.

Ответ: 400 400 способов.

Выбор из трех совокупностей без учета порядка; каждый вариант выбора из первой совокупности () может сочетаться с каждым вариантом выбора из второй (С) и с каждым вариантом выбора из третьей (С); по правилу произведения получаем:

способов выбора учащихся

Ответ: 1 866 000 способов.

11. Т. Сколькими способами группу из 12 человек можно разбить на две группы: а) по 4 и 8 человек; б) по 5 и 7 человек?

Количество способов разбиения множества на две части равно количеству способов формирования одной из частей (любой). Поскольку порядок расположения элементов не учитывается, имеем:

а)способов разбиения на 4 и 8 элементов.

б) способов разбиения на 5 и 7 элементов.

Ответ: а) 495 способов; б) 792 способа.

Замечание. Задача иллюстрирует свойство биноминальных коэффициентов:

12. Т. В отделе работают 5 ведущих и 8 старших научных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в командировку?

Выбор из двух разных совокупностей без учета порядка; каждый вариант выбора из первой совокупности (их С) может сочетаться с каждым вариантом выбора из второй совокупности (их С), по правилу произведения общее число способов выбрать сотрудников, уезжающих в командировку, равно:

= 560 способов.

Ответ: 560 способов.

13. М. Встретились 11 футболистов и 6 хоккеистов, и каждый стал по одному разу играть с каждым в шашки.

а) Сколько встреч было между футболистами?

б) Сколько встреч было между хоккеистами?

в) Сколько встреч было между футболистами и хоккеистами?

г) Сколько встреч было всего?

а) Выбираем пары из 11футболистов без учета порядка; количество возможных встреч:

б) Выбираем пары из 6 хоккеистов без учета порядка; количество встреч равно:

г) Общее количество встреч равно количеству пар из 11 + 6 = 17 элементов без учета порядка: Понятно, что сумма первых трех величин должна равняться последней: 55+ 15 + 66 = 136.

Ответ: а) 55; б) 15; в) 66; г) 136.

14. М. В правильном 17-угольнике провели все диагонали.

а) Сколько всего получилось отрезков?

б) Сколько имеется сторон?

в) Сколько провели диагоналей?

г) Сколько всего диагоналей в выпуклом n -угольнике?
Решение.

Правильный многоугольник имеет 17 вершин; никакие три из этих 17 точек не лежат на одной прямой.

а) Общее число отрезков равно количеству пар из 17 точек без учета порядка :

Можно рассуждать иначе. Пронумеруем вершины 17-угольника. Из каждой вершины, начиная с первой, исходит сторона 17-угольника, которая заканчивается в следующей по номеру вершине. Сторона, исходящая из 17-й вершины, заканчивается в вершине № 1. Поэтому количество сторон равно количеству вершин, т. е. 17.

в) Диагональю 17-угольника будет отрезок, соединяющий каждую вершину с каждой из вершин, не являющихся соседними для данной, т. е. с 17 - 1 - 2 = 14 разными вершинами (мы вычли 1 -вершину, из которой исходит диагональ, и 2 - две соседние вершины). Таким образом, из каждой вершины 17-угольника исходит 14 диагоналей. Но произведение 17 будет включать каждую диагональ дважды (сначала как исходящую из i -й вершины в k -ю, потом как исходящую из k -й вершины в i -ю). Поэтому общее количество диагоналей равно = 119. Понятно, что количество сторон плюс количество диагоналей должно равняться количеству отрезков:

г) В выпуклом n -угольнике из каждой вершины можно провести n - 1 - 2 = n -3 диагонали; общее количество диагоналей равно (объяснение такое же, как в пункте в).

Ответ: а) 136; б) 17; в) 119; г)

15. М. Встретились несколько человек и стали здороваться друг с другом. Известно, что рукопожатий было от 60 до 70. Сколько человек встретились, если известно, что:

а) каждый здоровался с каждым;

б) только один человек не здоровался ни с кем;

в) только двое не поздоровались между собой;

г) четверо поздоровались только между собой.

а) Число рукопожатий равно числу различных пар из п элементов без учета порядка выбора, поэтому: 60 ; 6070; 120 - n 140;

Можно решать двойное неравенство и выбрать натуральное п из полученного интервала. Однако в этом простейшем случае легко находится подбором: n = 12. При n = 11 n 2 - n = 110, а при n = 13 n 2 - n = 156.

б) Если один человек не здоровался ни с кем, то пары образовывались из n - 1 элемента, т. е. 60; 120 ( n - 1) ( n - 2) 140; поскольку 1211 =132, то n = 13.

в) Если двое не поздоровались между собой, то количество рукопожатий было на 1 меньше: 60; 61
122п(п-1)142. Поскольку 1211 = 132, то n = 12.

Ответ: а) 12; б) 13; в) 12; г) 15.

Афанасьев В.В. Теория вероятностей в примерах и задачах, - Ярославль: ЯГПУ , 1994.

Баврин И. И. Высшая математика: Учебник для студентов химико-математических специальностей педагогических вузов-2-е издание, переработанное. - М.:Просвещение, 1993.

Бунимович Е. А., Булычёв В.А. Вероятность и статистика. 5-9 классы: Пособие для общеобразовательных учебных заведений, - М.:Дрофа , 2005.

Виленкин Н. Я. и другие. Алгебра и математический анализ для 10 класса: Учебное пособие для учащихся школ и классов с углублённым изучением математики. - М.:Просвещение,1992.

Виленкин Н. Я. и другие. Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся школ и классов с углублённым изучением математики - М.:Просвещение, 1990.

Глейзер Г.И. История математики в школе: 9-10 класс. Пособие для учителей. - М.: Просвещение 1983.

Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Математика 9:Алгебра. Функции. Анализ данных - М.: Дрофа, 2000.

Колягин и другие. Алгебра и начала анализа 11 класс. Математика в школе - 2002 - №4 - с.43,44,46.

Люпшкас В.С. Факультативные курсы по математике: теория вероятностей: Учебное пособие для 9-11 классов.- М.,1991.

Макарычев Ю.Н., Миндюк Н.Г. Элементы статистики и теории вероятностей: Учебное пособие для учащихся 7-9 классов.- М.: Просвещение, 2005.

Мордкович А.Г., Семенов П.В. Алгебра и начала анализа 10 класс: Учебник для общеобразовательных учреждений (профильный уровень) – М.: Мнемозина, 2005.

Ткачева М.В., Федорова Н.Е. Элементы статистики и вероятность: Учебное пособие для учащихся 7-9 классов.- М.: Просвещение, 2005.

Предположим, что вы не можете вспомнить последнюю цифру телефона своего друга. Какое наибольшее количество номеров придется набрать, чтобы ему дозвониться?

Поскольку в конце телефонного номера может стоять любая из десяти цифр, то вам в худшем случае придется сделать десять попыток, тем самым перебрав все возможные варианты.

Нередко в повседневной жизни мы встречаемся с задачами, решение которых требует рассмотрения и подсчета всех возможных комбинаций. Поэтому такие задачи навзывают комбинаторными.

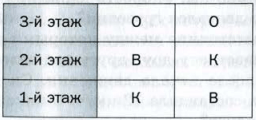
Пример 1 . Одноклассницы Оля, Валя и Катя дежурят по школе. Сколькими способами классный руководитель может расставить девочек по одной на каждом из трех этажей школы?

Решение. Предположим, что Олю назначили дежурить на третьем этаже. Тогда на втором этаже может дежурить Валя или Катя, а на первом − соответственно Катя или Валя.

Получаем два способа (две комбинации, два варианта) распределения дежурства (девочки обозначены первыми буквами их имен).

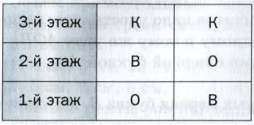
Пусть теперь дежурной на третьем этаже назначили Валю. Тогда на втором этаже может дежурить Оля или Катя, а на первом − соответственно Катя или Оля. Получаем еще два способа распределения дежурства.

И наконец, предположим, что дежурной на третьем этаже назначили Катю. Получаем еще два способа распределения дежурства.

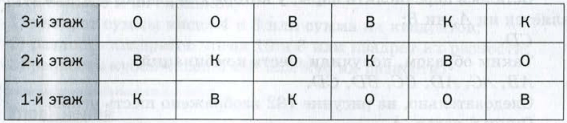
Таким образом получилось шесть способов распределения дежурства.

Ответ: 6 способов.

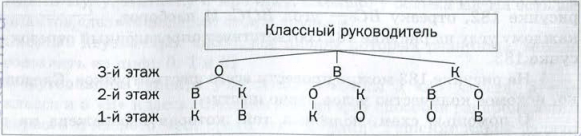
При решении комбнаторных задач важно рассмотреть (перебрать) все случаи. Поэтому процесс перебора желательно сделать удобным и наглядным.

Например, решение задачи о распределении дежурства можнго проиллюстрировать с помощью такой схемы:

Эта схема позволяет записать шесть комбинаций, каждая из которых соответствует одному варианту распределения дежурства: ОВК, ОКВ, ВОК, ВКО, КВО, КОВ.

Изображженная схема напоминает перевернутое дерево. Поэтому ее называют деревом возможных вариантов.

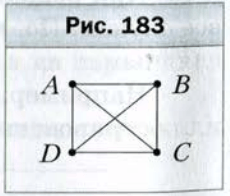
Пример 2 . Сколько углов изображено на рисунке 182 ?

Решение. Обозначение любого угла, изображенного на рисунке, состоит из трех букв, второй из которых обязательно является буква O, а две другие выбираются из букв A, B, C, D. Поэтому искомое количествоо углов равно количеству способов выбрать из букв A, B, C, D две буквы.

При записи всех возможных вариантов надо учесть, что, например, комбинации AB и BA соответствуют одному и тому же углу AOB.

Вначале перечислим все пары букв с первой A:

Теперь перечислим пары, у которых первая буква B, а вторая не является буквой A:

Осталось перечислить пары, у которых первая буква C, а второй не является ни A, ни B:

Таким образом, получили шесть комбинаций:

AB, AC, AD, BC, BD, CD.

Следовательно, на рисунке 182 изображено шесть углов.

При решении этой задачи можно воспользоваться такой наглядной схемой.

Рассмотрим четыре точки, обозначенные буквами A, B, C, D ( рис. 183 ).

Тогда количество отрезков, соединяющих каждые две точки, равно количеству углов, изображенных на рисунке 182 . Например, отрезку AC на рисунке 183 соответствует угол AOC на рисунке 182, отрезку BC − угол BOC. И наоборот, каждому углу на рисунке 182 соответствует определенный отрезок на рисунке 183 .

На рисунке 183 можно провести всего шесть отрезков. Следовательно, искомое количество углов равно шести.

С помощью схем, подобной той, которая изображена на рисунке 183, можно решать целый ряд задач. С помощью этой схемы решите такую задачу. При встрече четыре прямтеля обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (Ответ: 6 ).

Читайте также: