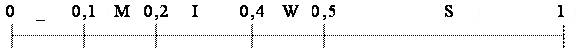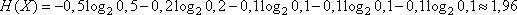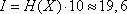Закодировать сообщение x математика

Обновлено: 18.05.2024

Арифметическое кодирование — один из алгоритмов энтропийного сжатия.

В отличие от алгоритма Хаффмана, не имеет жесткого постоянного соответствия входных символов группам бит выходного потока. Это даёт алгоритму большую гибкость в представлении дробных частот встречаемости символов.

Как правило, превосходит алгоритм Хаффмана по эффективности сжатия, позволяет сжимать данные с энтропией, меньшей 1 бита на кодируемый символ, но некоторые версии имеют патентные ограничения от компании IBM. [1]

Составив таблицу частоты появления символов, мы можем приступать к кодированию. На первом этапе составим рабочий отрезок. Выглядеть он будет так:

Т.о. мы с вами рассмотрели алгоритм кодирования и декодирования с помощью самого эффективного из всех энтропийных алгоритмов. Надеюсь, из этой статьи вы узнали что-то новое и поняли основные идеи, лежащие в алгоритме арифметического кодирования.

При арифметическом кодировании каждый символ кодируется нецелым числом бит, что эффективнее кода Хаффмана (теоретически, символу [math]a[/math] с вероятностью появления [math]p(a)[/math] допустимо ставить в соответствие код длины [math]-\log_2 p(a)[/math] , следовательно, при кодировании алгоритмом Хаффмана это достигается только с вероятностями, равными обратным степеням двойки).

На вход алгоритму передаются текст для кодирования и список частот встречаемости символов.

Рассмотрим отрезок [math][0; 1)[/math] на координатной прямой.
Поставим каждому символу текста в соответствие отрезок, длина которого равна частоте его появления.
Считаем символ из входного потока и рассмотрим отрезок, соответствующий этому символу. Разделим этот отрезок на части, пропорциональные частотам встречаемости символов.
Повторим пункт [math](3)[/math] до конца входного потока.
Выберем любое число из получившегося отрезка, которое и будет результатом арифметического кодирования.

[math]\mathtt\,[/math] — текст, подаваемый на вход;
[math]\mathtt\,[/math] — длина исходного текста;
[math]\mathtt\,[/math] — мощность алфавита исходного текста;
[math]\mathtt\,[/math] — массив символов, составляющих алфавит исходного текста;
[math]\mathtt\,[/math] — массив вероятностей обнаружения символа в тексте;

[math]\mathtt\,[/math] — структура, задающая подотрезок отрезка [math][0; 1)[/math] , соответствующего конкретному символу на основе частотного анализа. Имеет поля:

[math]\mathtt\,[/math] — левая граница подотрезка;
[math]\mathtt\,[/math] — правая граница подотрезка;

Замечание: для оптимизации размера кода можно выбрать из полученного на последнем шаге диапазона [math][left; right][/math] число, содержащее наименьшее количество знаков в двоичной записи.

Алгоритм по вещественному числу восстанавливает исходный текст.

Выберем на отрезке [math][0; 1)[/math] , разделенном на части, длины которых равны вероятностям появления символов в тексте, подотрезок, содержащий входное вещественное число. Символ, соответствующий этому подотрезку, дописываем в ответ.
Нормируем подотрезок и вещественное число.
Повторим пункты [math]1[/math] — [math]2[/math] до тех пор, пока не получим ответ.

[math]\mathtt\,[/math] — вещественное число, подаваемое на вход;
[math]\mathtt\,[/math] — длина восстанавливаемого текста;
[math]\mathtt\,[/math] — мощность алфавита исходного текста;
[math]\mathtt\,[/math] — массив символов, составляющих алфавит исходного текста;
[math]\mathtt\,[/math] — массив вероятностей обнаружения символа в тексте;

[math]\mathtt\,[/math] — левая граница подотрезка;
[math]\mathtt\,[/math] — правая граница подотрезка;
[math]\mathtt\,[/math] — значение символа.

Замечание: кодировщику и декодировщику должно быть известно, когда завершать работу. Для этого можно передавать в качестве аргумента длину текста или символ конца файла, после которого процесс должен быть остановлен.

Замечание: Несмотря на преимущества арифметического кодирования, существует проблема при его практическом применении из-за несовершенства представления чисел с плавающей точкой в памяти компьютера — поскольку некоторые дробные числа не могут быть точно представлены в двоичном коде, используемом современными процессорами (например, [math]\dfrac[/math] ), границы символов будут округлены, что может повлечь за собой неверную работу алгоритма при больших объёмах данных. В общем случае, алгоритм можно модифицировать так, чтобы результатом было дробное число. В такой реализации вероятность встречи символа представляется в виде рационального числа. Поскольку в каждой итерации будет переход из текущего отрезка в один из его [math]m[/math] подотрезков, кратных по длине [math]n[/math] , а всего итераций [math]n[/math] , в конечном результате знаменатель дроби не превысит [math]n^[/math] , а поскольку сумма всех вероятностей встречи символов равна [math]1[/math] , полученная дробь будет находиться в промежутке [math][0; 1)[/math] .

Метод Хаффмана является простым, но эффективным только в том случае, когда вероятности появления символов равны числам , где - любое целое положительное число. Это связано с тем, что код Хаффмана присваивает каждому символу алфавита код с целым числом бит. Вместе с тем в теории информации известно, что, например, при вероятности появления символа равной 0,4, ему в идеале следует поставить код длиной бит. Понятно, что при построении кодов Хаффмана нельзя задать длину кода в 1,32 бита, а только лишь в 1 или 2 бита, что приведет в результате к ухудшению сжатия данных. Арифметическое кодирование решает эту проблему путем присвоения кода всему, обычно, большому передаваемому файлу вместо кодирования отдельных символов.

Идею арифметического кодирования лучше всего рассмотреть на простом примере. Предположим, что необходимо закодировать три символа входного потока, для определенности – это строка SWISS_MISS с заданными частотами появления символов: S – 0,5, W – 0,1, I – 0,2, M – 0,1 и _ - 0,1. В арифметическом кодере каждый символ представляется интервалом в диапазоне чисел [0, 1) в соответствии с частотой его появления. В данном примере, для символов нашего алфавита получим следующие наборы интервалов:

Рис. 2. Распределение интервалов представление символов

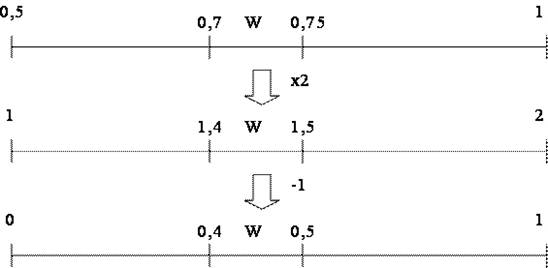
Процесс кодирования начинается со считывания первого символа входного потока и присвоения ему интервала из начального диапазона [0, 1). В данном случае для первого символа S получаем диапазон [0,5, 1). Затем, считывается второй символ – W, которому соответствует диапазон [0,4, 0,5). Но исходный диапазон [0, 1) уже сократился до [0,5, 1), поэтому символ W необходимо представить в этом новом диапазоне. Для этого достаточно вычислить новые нижнюю и верхнюю границы. Значение 0,4 будет соответствовать значению 0,7, а значение 0,5 – значению 0,75 (рис. 3).

Рис. 3. Схема представления новых границ символа W

Данные границы можно вычислить по формулам:

NewHigh = OldLow + (OldHigh-OldLow)*HighRange(X),

NewLow = OldLow + (OldHigh-OldLow)*LowRange(X),

где OldLow – нижняя граница интервала, в котором представляется текущий символ; OldHigh – верхняя граница интервала; HighRange(X) – исходная верхняя граница кодируемого символа; LowRange(X) – исходная нижняя граница кодируемого символа. Применяя данные формулы к вычислению границ символа W, получаем:

OldLow = 0,5, OldHigh = 1,

HighRange(W) = 0,5, LowRange(W) = 0,4,

NewHigh = 0,5 + (1-0,5)*0,5 = 0,75,

NewLow = 0,5 + (1-0,5)*0,4 = 0,7.

Аналогичным образом выполняется кодирование символа I, для которого новые интервалы также можно вычислить по приведенной формуле:

OldLow = 0,7, OldHigh = 0,75,

HighRange(I) = 0,4, LowRange(I) = 0,2,

NewHigh = 0,7 + (0,75-0,7)*0,4 = 0,72,

NewLow = 0,7 + (0,75-0,7)*0,2 = 0,71.

Ниже, в табл. 1 представлены значения границ при кодировании строки SWISS_MISS.

Символ	Границы
S	L H	0.0+(1.0-0.0)0.5 = 0.5 0.0+(1.0-0.0)1.0 = 1.0
W	L H	0.5+(1.0-0.5)0.4=0.70 0.5+(1.0-0.5)0.5=0.75
I	L H	0.7+(0.75-0.7)0.2=0.71 0.7+(0.75-0.7)0.4=0.72
S	L H	0.71+(0.72-0.71)0.5=0.715 0.71+(0.72-0.71)1.0=0.72
S	L H	0.715+(0.72-0.715)0.5=0.7175 0.715+(0.72-0.715)1.0=0.72
-	L H	0.7175+(0.72-0.7175)0.0=0.7175 0.7175+(0.72-0.7175)0.1=0.71775
М	L H	0.7175+(0.71775-0.7175)0.1=0.717525 0.7175+(0.71775-0.7175)0.2=0.717550
I	L H	0.717525+(0.717550-0.717525)0.4=0.717530 0.717525+(0.717550-0.717525)0.5=0.717535
S	L H	0.717530+(0.717535-0.717530)0.5=0.7175325 0.717530+(0.717535-0.717530)1.0=0.717535
S	L H	0.7175325+(0.717535-0.7175325)0.5=0.71753375 0.7175325+(0.717535-0.7175325)1.0=0.717535

Конечный выходной код – это последнее значение переменной Low, равное 0.71753375, из которого следует взять лишь восемь цифр 71753375 для записи в файл.

Теперь рассмотрим возможность восстановления закодированной информации по восьми цифрам 71753375 и известным интервалам символов. Первая из восьми цифр – это 7, т.е. 0,7. Она принадлежит одному из заданных интервалов [0.5, 1), который соответствует символу S. Поэтому первый декодированный символ – это S. Теперь вернемся к рис. 3 и заметим, что второй символ был представлен в интервале символа S, т.е. [0.5, 1). Но для удобства декодирования его лучше представить в исходном интервале [0, 1). Для этого достаточно интервал [0.5, 1) увеличить до начального, т.е. умножить на два и границы сдвинуть на величину 0.5*2=1 (рис. 4).

Рис. 4. Схема восстановления исходных интервалов символа W

Применяя данную схему к числу 0.71753375, получаем нижнюю границу следующего закодированного символа как будто он был начальным при кодировании:

Полученное значение принадлежит диапазону [0.4, 0.5), который соответствует символу W. Затем, также полученное число 0.4350675 следует нормировать, что в общем случае выполняется по формуле:

где Code – текущее значение кода. Например, пользуясь этой формулой применительно к коду 0.71753375, получаем значение

Code = (0.71753375-0.5)/(1-0.5)= 0.4350675,

которое в точности совпадает с предыдущей схемой вычисления. Аналогичным образом выполняется декодирование всех символов строки. В табл. 2 представлены коды, вычисляемые при декодировании символов. Здесь можно заметить, что процесс декодирования в данном случае можно остановить, если значение кода равно нулю.

Таблица 2. Вычисление кодов при декодировании

Символ	Code-Low	Область
S	0.71753375 – 0.5	= 0.21753375	/ 0.5 = 0.4350675
W	0.4350675 – 0.4	= 0.0350675	/ 0.1 = 0.350675
I	0.350675 – 0.2	= 0.150675	/ 0.2 = 0.753375
S	0.753375 – 0.5	= 0.253375	/ 0.5 = 0.50675
S	0.50675 – 0.5	= 0.00675	/ 0.5 = 0.0135
_	0.0135 – 0	= 0.0135	/ 0.1 = 0.135
M	0.135 – 0.1	= 0.035	/ 0.1 = 0.35
I	0.35 – 0.2	= 0.15	/ 0.2 = 0.75
S	0.75 – 0.5	= 0.25	/ 0.5 = 0.5
S	0.5 – 0.5	= 0	/ 0.5 = 0

Однако это не всегда так. Бывают случаи, когда ноль содержит в себе код очередного символа, а не означает конец процедуры декодирования. Здесь возникает проблема завершения декодирования. Для этого используют специальный символ eof, говорящий о том, что он является последним и декодирование последовательности можно завершить. При этом частота этого символа очевидно должна быть маленькой по сравнению с частотой символов алфавита последовательности, например, [0,999999 1).

Описанный выше процесс кодирования невозможно реализовать на практике, т.к. в нем предполагается, что в переменных Low и High хранятся числа с неограниченной точностью. По существу, результат кодирования – это вещественное число с очень большой точностью. Например, файл объемом 1Мб будет сжиматься, скажем, до 500 КБ, в котором будет записано одно число. Арифметические операции с такими числами реализовать сложно и долго. Поэтому любая практическая реализация арифметического кодера должна основываться на операциях с целыми числами, которые не должны быть слишком длинными. Рассмотрим такую реализацию, в которой переменные Low и High будут целыми числами длиной 16 или 32 бита. Эти переменные будут хранить верхние и нижние концы текущего подинтервала, но мы не будем им позволять неограниченно расти. Анализ табл. 1 показывает, что как только самые левые цифры переменных Low и High становятся одинаковыми, они уже не меняются в дальнейшем. Следовательно, эти цифры можно выдвинуть за скобки и работать с оставшейся дробной частью. После сдвига цифр мы будем справа дописывать 0 в переменную Low, а в переменную High – цифру 9. Для того, чтобы лучше понять весь процесс, можно представлять себе эти переменные как левый конец бесконечно длинного числа. Число Low имеет вид xxxx00… а число High = yyyy99…

Проблема состоит в том, что переменная High в начале должна равняться 1, однако мы интерпретируем Low и High как десятичные дроби меньшие 1. Решение заключается в присвоении переменной High значения 9999…, которое соответствует бесконечной дроби 0,9999…, равной 1.

Как это все работает? Закодируем этим способом ту же строку SWISS_MISS. Первая буква S определена диапазоном [0,5 1) и формально границы равны

но в нашем случае данные формулы следует преобразовать, чтобы переменные Low и High были целыми. Поэтому запишем их в таком виде:

но по условию граница High является открытой, т.е. не включает число 10000, поэтому от конечного значения нужно отнять 1:

Таким образом, получили формулы для вычисления целочисленных границ Low и High, и процесс кодирования будет выглядеть так (табл. 3).

S	L= H=	0+(10000-0)0.5 0+(10000-0)1.0-1	= =
W	L= H=	5000+(10000-5000)0.4 5000+(10000-5000)0.5	= =
I	L= H=	0+(5000-0)0.2 0+(5000-0)0.4-1	= =
S	L= H=	0+(10000-0)0.5 0+(10000-0)1.0-1	= =
S	L= H=	5000+(10000-5000)0.5 5000+(10000-5000)1.0-1	= =
_	L= H=	7500+(10000-7500)0.0 7500+(10000-7500)0.1-1	= =
M	L= H=	5000+(7500-5000)0.1 5000+(7500-5000)0.2	= =
I	L= H=	2500+(5000-2500)0.2 2500+(5000-2500)0.4-1	= =
S	L= H=	0+(5000-0)0.5 0+(5000-0)1.0-1	= =
S	L= H=	2500+(5000-2500)0.5 2500+(5000-2500)1.0-1	= =

На последнем шаге операции кодирования записываются все 4 цифры и полученная выходная последовательность имеет вид: 717533750.

Декодер работает в обратном порядке. В начале переменным Low и High присваиваются значения 0000 и 9999 соответственно, а переменной Code значение 7175. На основе этой информации требуется определить первый закодированный символ. Для этого число переменной Code нужно корректно представить в интервале от 0 до 1. В самом начале интервал такой и есть, поэтому частота символа, соответствующая значению Code будет равна

Эта частота попадает в диапазон [0,5 1) и соответствует символу S. Теперь границы Low и High пересчитываются, так как это делалось в кодере и принимают значения 5000 и 9999 соответственно. Так как значащие цифры этих переменных отличаются, то переменная Code остается прежней и величина

Это значение попадает в диапазон [0,4 0,5) и соответствует символу W. После этого величины Low и High принимают значения 7000 и 7499 и после отбрасывания значащей цифры переходят в 0000 и 4999 соответственно, а переменная Code преобразуется в 1753. Таким образом раскодируется вся последовательность.

На практике обычно значение index принимает целочисленные значения, которые вычисляются по формуле

и округляют до ближайшего целого.

Может показаться, что приведенный выше пример не производит никакого сжатия. Для того чтобы выяснить степень сжатия результаты кодирования нужно перевести в двоичную форму. Так как из конечного интервала

можно выбрать любое число, выберем наименьшее для хранения – это 717534, которому соответствует битовое представление 10101111001011011110 и составляет 20 бит. И строка из 10 символов сжимается в 20 бит. Хорошее ли это сжатие? Для этого нужно найти энтропию кодируемой последовательности и она будет равна

бит/сим

и составит величину

бит,

что в целых значениях равно 20 бит. Следовательно, полученный код достиг минимально возможного значения и является оптимальным. В общем случае можно показать, что при достаточно большой последовательности арифметический кодер всегда приводит к оптимальным результатам сжатия, т.е. является наилучшим среди всех энтропийных кодеров

Аннотация: В лекции подробно рассматривается арифметическое кодирование. Математическое доказательство его "выгодности" по отношению к другим методам кодирования. Проводится сравнение с другими методами кодирования. Очень хорошо освещены адаптивные алгоритмы сжатия информации, адаптивное арифметическое кодирование. Характерно большое количество примеров и заданий для самостоятельного изучения

При сжатии заданных данных, например, из файла все рассмотренные методы требуют двух проходов. Первый для сбора частот символов, используемых как приближенные значения вероятностей символов, и второй для собственно сжатия.

Пример арифметического кодирования. Пусть д.с.в. может принимать только два значения 0 и 1 с вероятностями 2/3 и 1/3 соответственно. Сопоставим значению 0 отрезок , а 1 - . Тогда для д.с.в. ,

$\dim(\vec X)=3,\; HX=H\vec X/3=\log_23-2/3\approx0.9183\hbox< бит/сим.></p> <p>,$

Шаг 2. Из текущего кода вычитается нижняя граница содержащего его интервала, полученная разность делится на длину этого же интервала. Полученное число считается новым текущим значением кода. Переход к шагу 1.

Упражнение 22 Декодировать арифметический код 011 для последовательности значений д.с.в. из предыдущего упражнения. Остановиться, после декодирования третьего символа.

Упражнение 24 д.с.в. может принимать три различных значения. При построении блочного кода с длиной блока 4 для необходимо будет рассмотреть д.с.в. - выборку четырех значений . Сколько различных значений может иметь ? Если считать сложность построения кода пропорциональной количеству различных значений кодируемой д.с.в., то во сколько раз сложнее строить блочный код для по сравнению с неблочным?

Читайте также: