Закодировать сообщение с помощью порождающей матрицы

Обновлено: 02.07.2024

Презентация на тему: " Цель: знакомство с матричным способом кодирования и декодирования информации. Задачи: изучить понятия: матрица; кодирующая матрица; произведение матриц." — Транскрипт:

2 Цель: знакомство с матричным способом кодирования и декодирования информации. Задачи: изучить понятия: матрица; кодирующая матрица; произведение матриц. выяснить, как осуществляется кодирование и декодирование информации при помощи матриц; изучить данный метод; составить задания вычисления произведений матриц.

3 Матрица – это прямоугольная таблица, составленная из элементов, имеющих произвольную природу. Матрицей размера mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрица, в которой одинаковое количество строк и столбцов, называется квадратной.

4 Будем использовать матрицы размером 2*2. Для того, чтобы воспользоваться способом шифровки с помощью матриц, достаточно уметь считать на уровне 6 класса, знать порядок букв в алфавите и правило умножения матриц. Расшифровать же его смогут только с помощью компьютера.

5 Для кодировки текста на русском языке пронумеруем все буквы по месту их расположения в алфавите – от 1 до 33, знак, пробел, тире, точка и т. д.(исходя из послания).

8 Получим 33, 34, 10, 34, 26, 10, 22, 18, что после перевода в буквы будет означать Я и шифр.

9 Вычислите произведения: Проверить

11 Вычислите произведения: Проверить

Линейные коды задаются с помощью порождающей G(x) и проверочной H(x) матриц. Эти матрицы связаны основным уравнением кодирования:

Матрица G(x) содержит k строк и n столбцов, ее элементами являются нули и единицы. В качестве строк матрицы G(x) выбираются любые ненулевые линейно независимые n-значные векторы, отстоящие друг от друга не менее чем на заданное кодовое расстояние d₀.

Векторы v₁, v₂, …, v_k называются линейно независимыми, если выполняется условие

где с_i=, а сложение выполняется по модулю два. То есть, каким бы образом мы не суммировали различные строки матрицы G(x), не получим суммы, равной нулю. Все множество кодовых слов состоит из строк порождающей матрицы и всевозможных комбинаций этих строк, т.е. суммы по модулю два всех строк матрицы G(x) сначала попарно, затем по три и так далее до суммы всех k строк.

С точки зрения алгебры все кодовые слова образуют некоторое векторное пространство, базисом которого являются строки матрицы G(x).

Поскольку линейно независимые векторы могут быть выбраны произвольным образом, то, очевидно, можно построить множество матриц G(x) с одним и тем же кодовым расстоянием d₀.

Свойство линейной независимости векторов инвариантно относительно двух следующих операций (выполняя эти две операции, кодовое расстояние не меняется):

1) возможна произвольная перестановка строк и столбцов в матрице G(x);

2) замена i-й строки на сумму i-й и j-й строк и т. д. (эту операцию нельзя осуществлять со столбцами матрицы G(x)).

Производя вышеуказанные операции, любую произвольную матрицу G(x) можно привести к так называемому приведенно-ступенчатому (каноническому) виду:

где I_k –единичная подматрица размерностью k×k,

H * T – транспонированная проверочная матрица (транспонировать – значит поменять местами строки и столбцы).

Исходя из основного уравнения кодирования, проверочная матрица имеет вид

Возьмем порождающую матрицу кода (7,4). В этой матрице количество строк равно 4 (k=4), а количество столбцов 7(n=7).

G(x)=0 1 0 0 1 1 1

Для того чтобы построить проверочную матрицу, необходимо транспонировать подматрицу G(x) * и к ней приписать единичную матрицу размером l×l. Проверочная матрица будет иметь размер l×n, l = n-k=7-4=3, т.е. матрица Н(x) имеет размер 3×7.

H(x)=0 1 1 1 0 1 0

Операция кодирования информации линейным кодом заключается в умножении информационного вектора A_k размерностью k на порождающую матрицу G(x); в результате получаем вектор

Кодовую последовательность на выходе кодера можно записать в виде:

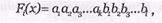
где a₁a₂a₃. а_k - информационные символы (логические 1 и 0),

b₁b₂b₃. b₁ - проверочные символы (логические 1 и 0).

Проверочные символы b₁b₂b₃. b_l формируются путем суммирования по модулю два информационных символов, стоящих на определенных позициях.

Алгоритм формирования проверочных символов в общем виде можно записать так:

где c_j₁c_j₂. c_jk- коэффициенты принимающие значение логических 1 и 0.

G(x)=0 1 0 0 1 1 1

Следовательно, F(x)=A_k(x)×G(x)=[1010]* 0 1 0 0 1 1 1 = [1010 011]

Рассмотрим построение и реализацию устройства кодирования ЛБК (7,4).

Порождающая и проверочная матрицы этого кода имеют вид:

1 0 0 0 1 0 1 1 1 1 0 1 0 0

G(x)=0 1 0 0 1 1 1 H(x)=0 1 1 1 0 1 0

0 0 1 0 1 1 0 1 1 0 1 0 0 1

Этот код имеет d=3 и исправляет все одиночные ошибки и обнаруживает двойные. Символы а₁,а₂,а₃,а₄ – информационные символы, b₁,b₂,b₃ – проверочные.

По матрице запишем проверочные уравнения:

Таким образом, кодер состоит из (n-k)=7-4=3 сумматоров по модулю два, выходы которых соответствуют (n-k) проверочным символам.

Устройство кодирования линейного группового кода (7, 4) приведено на рисунке.

Рисунок – Кодер линейного группового кода (6, 3)

Пример 2.1. Сформировать кодовую последовательность ЦК с параметрами (n,k,d₀)=(10,5,5), если Р(х)=х 5 +х 4 +х 2 +1.

Решение: переводим Р(х) из записи в форме полинома в двоичную форму записи, Р(х)=х 5 +х 4 +х 2 +1=110101. Далее формируем первую строку матрицы G_5,10(х) следующим образом: двоичную последовательность 110101 дополняем справа четырьмя нулями; в результате получаем разрешенную кодовую последовательность вида 1101010000 длиной n=10 двоичных символов. Следующий шаг – выполнение (k-1)=(5-1)=4 циклических сдвига двоичных символов первой строки G(x).

В результате получаем следующую порождающую матрицу

Этот способ построения порождающей матрицы G_5,10(х) можно рассмотреть со следующей позиции:

а) переводим Р(х) из записи в форме полинома в форму двоичной последовательности (можно и не переводить), т.е. Р(х)=х 5 +х 4 +х 2 +1=110101;

б) умножаем Р(х)=110101 на одночлен вида х k -1 , т. е. на 1000; в результате получаем первую строку или первую разрешенную кодовую последовательность 1101010000, а далее используем рассмотренную методику, т.е. циклический сдвиг двоичных символов первой строки (k-1) раз.

В общем случае построение порождающей матрицы G(x) ЦК с использованием образующего полинома можно записать так:

Формирование кодовой последовательности F(x), т. е. процесс кодирования информации с помощью G(x) осуществляется по правилу F(x)=Q(x)∙G(x): первый символ Q(x) умножаем на первый символ первого столбца G(x), второй символ Q(x) умножаем на второй символ первого столбца G(x) и суммируем по модулю два с первым результатом, третий символ Q(x) умножаем на третий символ первого столбца G(x) и суммируем по модулю два с предыдущим результатом и т.д. Затем первый символ Q(x) умножаем на первый символ второго столбца G(x) и далее все повторяется аналогично формированию первого кодового символа F(x).

Пример 2.2. Рассмотрим способ формирования кодовых последовательностей ЦК с использованием единичной матрицы и остатков от деления х n -1 /Р(х).

Для рассмотрения сущности формирования кодовых последовательностей ЦК используем данные предыдущего примера.

Так как k=5, то используем единичные векторы: Q₁(x)=10000, Q₂(x)=01000, Q₃(x)=00100, Q₄(x)=00010, Q₅(x)=00001. Записываем Q₁(x)…Q₅(x) в виде единичной подматрицы рангом (5 ´ 5).

Далее определяем проверочные символы каждой строки по следующей методике: делим х n -1 /Р(х) и берем остатки от деления для первой строки – от первого такта деления, т.е. R₁(x), для второй строки – после двух тактов деления, т.е. R₂(x) и т.д. Полученные символы дописываем к соответствующим строкам единичной подматрицы:

Формирование кодовых последовательностей осуществляется по правилу, приведенному в примере 2.1, т.е. F(x)=Q(x)∙G_5,10(x).

В области математики и теории информации линейный код — это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации.

Содержание

Основы

В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).

В системах связи возможны несколько стратегий борьбы с ошибками:

обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется в основном на канальном и транспортном уровнях;
обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
исправление ошибок (англ.forward error correction ) применяется на физическом уровне.

Коды обнаружения и исправления ошибок

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и сверточные, работающие с данными как с непрерывным потоком.

Блоковые коды

$R = \frac<k> Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают (n,k) . При этом число$
называется скоростью кода.

Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:

способность исправлять как можно большее число ошибок,
как можно меньшая избыточность,
простота кодирования и декодирования.

Нетрудно видеть, что приведенные требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.

Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую легкость кодирования и декодирования.

Линейные пространства

Порождающая матрица

Пусть векторы = (x_. x_), \overrightarrow = (x_. x_). \overrightarrow = (x_. x_)" width="" height="" />
являются базисом линейного пространства C . По определению базиса, любой вектор \in C" width="" height="" />
можно представить в виде линейной комбинации базисных векторов: = \overrightarrow + \overrightarrow + . + \overrightarrow" width="" height="" />
, либо в матричной форме, как:

$\overrightarrow<v> = (,. ) \begin x_ & x_ & .. & x_\\ x_ & x_ & .. & x_\\ .. & .. & .. & ..\\ x_ & x_ & .. & x_\\ \end = \overrightarrowG$
,

$G = \begin где x_ & x_ & .. & x_\\ x_ & x_ & .. & x_\\ .. & .. & .. & ..\\ x_ & x_ & .. & x_\\ \end$
называется порождающей матрицей линейного пространства.

Это соотношение устанавливает связь между векторами коэффициентов = (,. )" width="" height="" />
и векторами \in C" width="" height="" />
. Перечисляя все векторы коэффициентов = (,. ) " width="" height="" />
можно получить все векторы \in C" width="" height="" />
. Иными словами, матрица G порождает линейное пространство.

Проверочная матрица

Другим способом задания линейных пространств является описание через проверочную матрицу.

Пусть " width="" height="" />
— линейное k-мерное пространство над полем _q" width="" height="" />
и " width="" height="" />
— ортогональное дополнение " width="" height="" />
. Тогда по одной из теорем, размерность " width="" height="" />
равна r = n − k . Поэтому в " width="" height="" />
существует r базисных векторов. Пусть _1 = (_1>. _n>), \overrightarrow_2 = (_1>. _n>). \overrightarrow_r = (_1>. _n>) " width="" height="" />
базис в " width="" height="" />
.

$\overrightarrow<v> Тогда любой вектор \in C$
удовлетворяет следующей системе линейных уравнений:

$\begin h_ x_1 + h_ x_2 + . + h_ x_n = 0 \\ h_ x_1 + h_ x_2 + . + h_ x_n = 0 \\ . \\ h_ x_1 + h_ x_2 + . + h_ x_n = 0 \end$

$\overrightarrow<v> Или в матричной форме: H^T = 0$
,

$H = \begin где \overrightarrow_1\\ \overrightarrow_2\\ . \\ \overrightarrow_r\\ \end = \begin h_ & h_ & .. & h_\\ h_ & h_ & .. & h_\\ .. & .. & .. & ..\\ h_ & h_ & .. & h_\\ \end$
— проверочная матрица.

$\mathbb<H> Приведенную систему линейных уравнений следует рассматривать, как систему проверок для всех векторов линейного пространства, поэтому матрица$
называется проверочной матрицей.

Формальное определение

Линейный код длины n и ранга k является линейным подпространством C размерности k векторного пространства _q^n" width="" height="" />
, где _q" width="" height="" />
— конечномерное поле из q элементов. Такой код с параметром q называется q-арным кодом (напр. если q = 5 — то это 5-арный код). Если q = 2 или q = 3, то код представляет собой двоичный код, или тернарный соответственно.

Линейный (блоковый) код — такой код, что множество его кодовых слов образует k -мерное линейное подпространство (назовем его C ) в n -мерном линейном пространстве, изоморфное пространству k -битных векторов.

Это значит, что операция кодирования соответствует умножению исходного k -битного вектора на невырожденную матрицу G , называемую порождающей матрицей.

Пусть " width="" height="" />
— ортогональное подпространство по отношению к C , а H — матрица, задающая базис этого подпространства. Тогда для любого вектора \in C" width="" height="" />
справедливо:

$\overrightarrow<v> H^T = \overrightarrow$
.

Свойства и важные теоремы

Минимальное расстояние и корректирующая способность

Минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов.

Вес вектора — w расстояние Хемминга между этим вектором и нулевым вектором, иными словами — число ненулевых компонент вектора.

Минимальное расстояние d линейного кода равно минимальному из весов Хемминга ненулевых кодовых слов:

$d = \min_<\overrightarrow \in C, \overrightarrow \not = \overrightarrow>( w( \overrightarrow) )$

Доказательство:

Расстояние между двумя векторами , \overrightarrow)" width="" height="" />
удовлетворяет равенству , \overrightarrow) = w(\overrightarrow - \overrightarrow)" width="" height="" />
, где )" width="" height="" />
— вес Хемминга вектора " width="" height="" />
. Из того, что разность любых двух кодовых слов линейного кода также является кодовым словом линейного кода, вытекает утверждение теоремы: \in C, \overrightarrow \not = \overrightarrow>w( \overrightarrow)" width="" height="" />

Минимальное расстояние Хемминга d является важной характеристикой линейного блокового кода. Она определяет другую, не менее важную характеристику — корректирующую способность:

Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внес ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем B. Но если каналом были внесены ошибки в двух битах, декодер может посчитать, что было передано слово B.

Число обнаруживаемых ошибок — число ошибок, при котором код может судить об ошибочной ситуации. Это число равно

f = d − 1 .

Теорема 2 (без доказательства):

Если любые l столбцов проверочной матрицы H линейного (n, k)-кода линейно независимы, то минимальное расстояние кода равно по меньшей мере d. Если при этом найдутся d линейно зависимых столбцов, то минимальное расстояние кода равно d в точности.

Теорема 3 (без доказательства):

Если минимальное расстояние линейного (n, k)-кода равно d, то любые l столбцов проверочной матрицы H линейно независимы и найдутся d линейно зависимых столбцов.

Коды Хемминга

=\overrightarrow H^T" width="" height="" />
, где " width="" height="" />
— принятый вектор,

будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.

Код Рида-Малера

Код Рида-Малера [en:Reed-Muller code] — линейный код.

Общий метод кодирования линейных кодов

$\overrightarrow<g_1> Линейный код длины n с k информационными символами является k-мерным линейным подпространством, поэтому каждое кодовое слово является линейной комбинацией базисных векторов = (g_. g_), \overrightarrow = (g_. g_). \overrightarrow = (g_. g_)$
подпространства:

$\overrightarrow<c> = \overrightarrow + \overrightarrow + . + \overrightarrow$
.

Либо с помощью порождающей матрицы:

= \overrightarrow G = (,. ) \begin g_ & g_ & .. & g_\\ g_ & g_ & .. & g_\\ .. & .. & .. & ..\\ g_ & g_ & .. & g_\\ \end " width="" height="" />
, где = (. ), . \in \mathbb" width="" height="" />

Это соотношение есть правило кодирование, по которому информационное слово = (. )" width="" height="" />
отображается в кодовое = (. )" width="" height="" />

Общий метод обнаружения ошибок в линейном коде

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова " width="" height="" />
соответствует наиболее вероятное переданное слово " width="" height="" />
. Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора " width="" height="" />
вычисляется синдром =\overrightarrow H^T" width="" height="" />
. Поскольку = \overrightarrow + \overrightarrow" width="" height="" />
, где " width="" height="" />
— кодовое слово, а " width="" height="" />
— вектор ошибки, то =\overrightarrow H^T" width="" height="" />
. Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Линейные циклические коды

Несмотря на то, что исправление ошибок в линейных кодах уже значительно проще исправления в большинстве нелинейных, для большинства кодов этот процесс все ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.

$\overrightarrow<v> Циклическим кодом является линейный код, обладающий следующим свойством: если$
является кодовым словом, то его циклическая перестановка также является кодовым словом.

$\overrightarrow<v> Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово = (v_0, v_1, . v_)$
представляется в виде полинома v(x) = v₀ + v₁x + . + v_{n − 1}x n − 1 . При этом циклический сдвиг кодового слова эквивалентен умножению многочлена на x по модулю x n − 1 .

В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть v₀,v₁ … могут принимать значения 0 или 1.

Порождающий полином

Можно показать, что все кодовые слова конкретного циклического кода кратны определенному порождающему полиному g(x) . Порождающий полином является делителем x n − 1 .

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:

Коды CRC

Таким образом, вид полинома g(x) задает конкретный код CRC. Примеры наиболее популярных полиномов:

название кода	степень	полином
CRC-12	12	x 12 + x 11 + x 3 + x 2 + x + 1
CRC-16	16	x 16 + x 15 + x 2 + 1
CRC-x 16 + x 15 + x 5 + 1
CRC-32	32	x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1

Коды БЧХ

Коды Боуза-Чоудхури-Хоквингема (БЧХ) являются подклассом двоичных циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.

Математически построение кодов БЧХ и их декодирование используют разложение порождающего полинома g(x) на множители в поле Галуа.

Коды Рида-Соломона

Коды Рида-Соломона (РС-коды) фактически являются недвоичными кодами БЧХ, то есть элементы кодового вектора являются не битами, а группами битов. Очень распространены коды Рида-Соломона, работающие с байтами (октетами).

Преимущества и недостатки линейных кодов

Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока. Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.

Оценка эффективности

Граница Хемминга и совершенные коды

Пусть имеется двоичный блоковый (n,k) код с корректирующей способностью t . Тогда справедливо неравенство (называемое границей Хемминга):

$\sum_<i=0> ^t \le 2^$
.

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида-Соломона) не являются совершенными.

Энергетический выигрыш

При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определенных системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.

Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.

Читайте также: