Совершенные нормальные формы сообщение
Обновлено: 29.06.2024
Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).
Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.
ДНФ записывается в следующей форме: F1 ∨ F2 ∨ . ∨ Fn, где Fi - элементарная конъюнкция
Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой конъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
КНФ записывается в следующей форме: F1 ∧ F2 ∧ . ∧ Fn, где Fi - элементарная дизъюнкция
Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ .
Алгоритм построения СДНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно единице.
- Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Алгоритм построения СКНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно нулю.
- Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные дизъюнкции связываем операциями конъюнкции.
Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае - СКНФ.
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
| x | y | z | F (x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Проверим полученную формулу. Для этого построим таблицу истинности функции.
| x | y | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F (x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.
Определение 5. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ее ДНФ, обладающая следующими свойствами:
1. Она не содержит двух одинаковых слагаемых.
2. Ни одно слагаемое не содержит одновременно двух одинаковых сомножителей.
3. Ни одно слагаемое не содержит одновременно некоторого высказывания и его отрицания.
4. Каждое слагаемое содержит в качестве сомножителя либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Это определение является конструктивным, т.е. позволяет для каждой формулы алгебры высказываний, приведенной к ДНФ, построить ее СДНФ.
Упражнение 2.2.5
Задана ДНФ. Приведем ее к СДНФ.
1. Первое и последние слагаемые одинаковы. На основании свойства операции дизъюнкции АÚА=А одно из одинаковых слагаемых можно отбросить.
Теперь выполнили условия 1 – 3. Чтобы выполнить условие 4, поступим следующим образом:
Теперь условие 4 выполнено, но появились одинаковые слагаемые. Исключив их, получим:
Определение 6. Совершенной конъюнктивной нормальной формой данной формулы алгебры высказываний (СКНФ) называется такая ее КНФ, которая удовлетворяет следующим свойствам:
1. Она не содержит двух одинаковых сомножителей.
2. Ни один из сомножителей не содержит одновременно двух одинаковых слагаемых.
3. Ни один из сомножителей не содержит одновременно некоторого высказывания и его отрицания.
4. Каждый сомножитель СКНФ содержит в качестве слагаемого либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Определение СКНФ также является конструктивным.
Упражнение 2.2.6
Из определений и теорем 3, 4 следует, что тождественно истинная формула не имеет СКНФ, а тождественно ложная – СДНФ.
Каждая не тождественно истинная и не тождественно ложная формула имеет единственную СКНФ и СДНФ.
Совершенные нормальные формы могут быть применены для установления равносильности двух заданных формул алгебры высказываний. Для этого нужно обе формулы привести к СКНФ или СДНФ и убедить в их совпадении. Например, формулы
Полной элементарной конъюнкцией называется конъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 5. Аналогично, полной элементарной суммой называется элементарная дизъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 6.
Поэтому совершенные нормальные формы можно определить так:
Определение 7. Совершенной дизъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией различных полных элементарных конъюнкций.
Определение 8. Совершенной конъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией различных полных элементарных дизъюнкций.
Каждая полная элементарная конъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 1: переменное высказывание, входящее без знака отрицания, принимает значение 1, а со знаком отрицания – 0. Этот набор значений элементарных составляющих называется единицей данной полной элементарной конъюнкции. Так, единицей полной элементарной конъюнкции является (1, 0,1).
Аналогично каждая полная элементарная дизъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 0: переменное высказывание, входящее без знака отрицания, принимает значение 0, а со знаком отрицания – 1. Этот набор значений элементарных составляющих называется нулем данной полной элементарной дизъюнкции. Так, нулем полной элементарной дизъюнкции является (1, 1,0).
Эти сведения непосредственно используются в следующем разделе данного учебного пособия.
Построение формулы алгебры высказываний
по заданной логической функции
Рассмотрим задачу, обратную той, о которой шла речь в разделах 2.1, 2.2 – построение функции для некоторой формулы алгебры высказываний. Задана некоторая функция f(x1, x2, . xn), нужно построить для нее формулу S. Задача эта неоднозначна, существует множество равносильных между собой формул, соответствующих этой функции. Будем строить совершенную нормальную форму. При этом учтем, что полная элементарная дизъюнкция имеет единственный ноль, а полная элементарная конъюнкция – единственную единицу. Решение задачи рассмотрим на примере.

Таблица 2.3.1
Пусть задана некоторая функция трех аргументов f(1,1,1)=f(1,0,0)=f(0,1,0)=1. Это значит, что на наборах (1,1,1), (1,0,0), (0,1,0) функция принимает значение 1, а на остальных наборах – 0.
Построим S в виде совершенной дизъюнктивной нормальной формы. Так как S не тождественно ложна, это можно сделать. СДНФ состоит из стольких слагаемых, сколько единиц содержит функция. Первому значению 1 соответствует слагаемое xyz, принимающее значение 1 при х=1, y=1, z=1. Второму значению 1 соответствует слагаемое , принимающее значение 1 при х=1, y=0, z=0. Аналогично третье слагаемое, соответствующее 1, стоящей в шестой строке таблицы f, есть . Следовательно, . Итак:
1) Совершенная дизъюнктивная нормальная форма содержит столько слагаемых, сколько единиц имеет функция.
2) Эти единицы соответствуют тем наборам переменных, при которых каждое слагаемое (элементарная конъюнкция) обращается в единицу, т.е. переменным, входящим в элементарную конъюнкцию без знака отрицания, соответствует значение 1, а со знаком отрицания – 0.
Чтобы написать СКНФ по заданной функции, нужно выбрать все значения 0, встречающиеся в ней, и рассмотреть наборы значений переменных, отвечающие этим нулям. В заданном примере таблица содержит пять нулей. Первому значению 0 отвечает сомножитель , обращающийся в 0 при х=1, y=1, z=0. Второму – при х=1, y=0, z=1 и т.д. В результате получим
1. СДНФ содержит столько сомножителей, сколько нулей имеет истинностная таблица.
2. Эти нули соответствуют тем наборам переменных, при которых каждый сомножитель (каждая элементарная сумма) обращается в 0, т.е. переменным, входящим в элементарную сумму без знака отрицания, соответствует значение 0, а со знаком отрицания – 1.
Заметим, что, используя список основных равносильных формул, полученные выражения для S упрощают, если это возможно.
Моделирование алгебры высказываний
с помощью релейно-контактных схем
Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие – разомкнуты.
Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x1, . xn, а размыкающие – .
Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных хi, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.
Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:
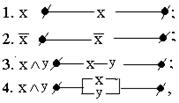
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция – последовательным.
Упражнение 2.3.1
Построить функцию проводимости следующей схемы:

Функция проводимости для такой схемы задается, очевидно, следующей таблицей:
Таблица 2.3.2
По данной логической функции построим формулу – СКНФ:
Упростим это выражение: .
Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:

Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере, .
Упражнение 2.3.2
Построить наиболее простую релейно-контактную схему по заданной функции проводимости f(x,y,z): f(0,1,0) =
= f(1,1,0) = f(1,1,1)=0.
Далее упрощаем формулу S:
Определение 5. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ее ДНФ, обладающая следующими свойствами:
1. Она не содержит двух одинаковых слагаемых.
2. Ни одно слагаемое не содержит одновременно двух одинаковых сомножителей.
3. Ни одно слагаемое не содержит одновременно некоторого высказывания и его отрицания.
4. Каждое слагаемое содержит в качестве сомножителя либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Это определение является конструктивным, т.е. позволяет для каждой формулы алгебры высказываний, приведенной к ДНФ, построить ее СДНФ.
Упражнение 2.2.5
Задана ДНФ. Приведем ее к СДНФ.
1. Первое и последние слагаемые одинаковы. На основании свойства операции дизъюнкции АÚА=А одно из одинаковых слагаемых можно отбросить.
Теперь выполнили условия 1 – 3. Чтобы выполнить условие 4, поступим следующим образом:
Теперь условие 4 выполнено, но появились одинаковые слагаемые. Исключив их, получим:
Определение 6. Совершенной конъюнктивной нормальной формой данной формулы алгебры высказываний (СКНФ) называется такая ее КНФ, которая удовлетворяет следующим свойствам:
1. Она не содержит двух одинаковых сомножителей.
2. Ни один из сомножителей не содержит одновременно двух одинаковых слагаемых.
3. Ни один из сомножителей не содержит одновременно некоторого высказывания и его отрицания.
4. Каждый сомножитель СКНФ содержит в качестве слагаемого либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.
Определение СКНФ также является конструктивным.
Упражнение 2.2.6
Из определений и теорем 3, 4 следует, что тождественно истинная формула не имеет СКНФ, а тождественно ложная – СДНФ.
Каждая не тождественно истинная и не тождественно ложная формула имеет единственную СКНФ и СДНФ.
Совершенные нормальные формы могут быть применены для установления равносильности двух заданных формул алгебры высказываний. Для этого нужно обе формулы привести к СКНФ или СДНФ и убедить в их совпадении. Например, формулы
Полной элементарной конъюнкцией называется конъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 5. Аналогично, полной элементарной суммой называется элементарная дизъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 6.
Поэтому совершенные нормальные формы можно определить так:
Определение 7. Совершенной дизъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией различных полных элементарных конъюнкций.
Определение 8. Совершенной конъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией различных полных элементарных дизъюнкций.
Каждая полная элементарная конъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 1: переменное высказывание, входящее без знака отрицания, принимает значение 1, а со знаком отрицания – 0. Этот набор значений элементарных составляющих называется единицей данной полной элементарной конъюнкции. Так, единицей полной элементарной конъюнкции является (1, 0,1).
Аналогично каждая полная элементарная дизъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 0: переменное высказывание, входящее без знака отрицания, принимает значение 0, а со знаком отрицания – 1. Этот набор значений элементарных составляющих называется нулем данной полной элементарной дизъюнкции. Так, нулем полной элементарной дизъюнкции является (1, 1,0).
Эти сведения непосредственно используются в следующем разделе данного учебного пособия.
Построение формулы алгебры высказываний
по заданной логической функции
Рассмотрим задачу, обратную той, о которой шла речь в разделах 2.1, 2.2 – построение функции для некоторой формулы алгебры высказываний. Задана некоторая функция f(x1, x2, . xn), нужно построить для нее формулу S. Задача эта неоднозначна, существует множество равносильных между собой формул, соответствующих этой функции. Будем строить совершенную нормальную форму. При этом учтем, что полная элементарная дизъюнкция имеет единственный ноль, а полная элементарная конъюнкция – единственную единицу. Решение задачи рассмотрим на примере.
Таблица 2.3.1
Пусть задана некоторая функция трех аргументов f(1,1,1)=f(1,0,0)=f(0,1,0)=1. Это значит, что на наборах (1,1,1), (1,0,0), (0,1,0) функция принимает значение 1, а на остальных наборах – 0.
Построим S в виде совершенной дизъюнктивной нормальной формы. Так как S не тождественно ложна, это можно сделать. СДНФ состоит из стольких слагаемых, сколько единиц содержит функция. Первому значению 1 соответствует слагаемое xyz, принимающее значение 1 при х=1, y=1, z=1. Второму значению 1 соответствует слагаемое , принимающее значение 1 при х=1, y=0, z=0. Аналогично третье слагаемое, соответствующее 1, стоящей в шестой строке таблицы f, есть . Следовательно, . Итак:
1) Совершенная дизъюнктивная нормальная форма содержит столько слагаемых, сколько единиц имеет функция.
2) Эти единицы соответствуют тем наборам переменных, при которых каждое слагаемое (элементарная конъюнкция) обращается в единицу, т.е. переменным, входящим в элементарную конъюнкцию без знака отрицания, соответствует значение 1, а со знаком отрицания – 0.
Чтобы написать СКНФ по заданной функции, нужно выбрать все значения 0, встречающиеся в ней, и рассмотреть наборы значений переменных, отвечающие этим нулям. В заданном примере таблица содержит пять нулей. Первому значению 0 отвечает сомножитель , обращающийся в 0 при х=1, y=1, z=0. Второму – при х=1, y=0, z=1 и т.д. В результате получим
1. СДНФ содержит столько сомножителей, сколько нулей имеет истинностная таблица.
2. Эти нули соответствуют тем наборам переменных, при которых каждый сомножитель (каждая элементарная сумма) обращается в 0, т.е. переменным, входящим в элементарную сумму без знака отрицания, соответствует значение 0, а со знаком отрицания – 1.
Заметим, что, используя список основных равносильных формул, полученные выражения для S упрощают, если это возможно.
Моделирование алгебры высказываний
с помощью релейно-контактных схем
Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие – разомкнуты.
Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x1, . xn, а размыкающие – .
Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных хi, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.
Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция – последовательным.
Упражнение 2.3.1
Построить функцию проводимости следующей схемы:

Функция проводимости для такой схемы задается, очевидно, следующей таблицей:
Таблица 2.3.2
По данной логической функции построим формулу – СКНФ:
Упростим это выражение: .
Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:

Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере, .
Упражнение 2.3.2
Построить наиболее простую релейно-контактную схему по заданной функции проводимости f(x,y,z): f(0,1,0) =
= f(1,1,0) = f(1,1,1)=0.
Для каждой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую из логических связок лишь отрицание, конъюнкцию и дизъюнкцию. Для этого нужно, используя равносильности теоремы 4.4, пункты у), ч), выразить все имеющиеся в формуле импликации и эквивалентности через отрицание, конъюнкцию и дизъюнкцию. Так, для формулы равносильной ей формулой, не содержащей логических связок . Выразить данную формулу через отрицание, конъюнкцию и дизъюнкцию возможно не одним способом, а многими. К примеру, рассматриваемая формула равносильна также следующим формулам, содержащим из логических связок лишь и
Среди всевозможных выражений данной формулы через конъюнкцию, дизъюнкцию и отрицание некоторые играют важную роль как в алгебре высказываний, так и в ее приложениях. Рассмотрение таких выражений, называемых совершенными нормальными формами , и составляет цель настоящего параграфа.
Понятие нормальных форм
Конъюнктивным одночленом от переменных называется конъюнкция этих переменных или их отрицаний. Здесь "или" употребляется в неисключающем смысле, т.е. в конъюнктивный одночлен может входить одновременно и переменная, и ее отрицание. Приведем несколько примеров конъюнктивных одночленов:
Дизъюнктивным одночленом от переменных называется дизъюнкция этих переменных или их отрицаний (и здесь союз "или" употребляется в неисключающем смысле). Приведем примеры дизъюнктивных одночленов:
Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов, т.е. выражение вида , где все , являются конъюнктивными одночленами (не обязательно различными). Аналогично конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов , где все , являются дизъюнктивными одночленами (не обязательно различными). Будем также называть дизъюнктивной (конъюнктивной) нормальной формой указанные выражения при .
Нормальную форму, представляющую формулу нормальной формой этой формулы .
Нетрудно понять, что всякая формула обладает как дизъюнктивной, так и конъюнктивной нормальными формами. В самом деле, всякую формулу можно выразить через конъюнкцию, дизъюнкцию и отрицание. Используя законы де Моргана (теорема 4.4, пункты р) и с)) и свойство дистрибутивности конъюнкции относительно дизъюнкции (теорема 4.4, пункт м)), можем преобразовать равносильным образом полученное выражение к дизъюнкции конъюнктивных одночленов (к дизъюнктивной нормальной форме). Если же к исходному выражению применить свойство дистрибутивности дизъюнкции относительно конъюнкции (теорема 4.4, пункт н)), то его можно свести к конъюнкции дизъюнктивных одночленов (к конъюнктивной нормальной форме).
Очевидно, что у данной формулы (последнее действие в них — умножение) называются одночленами, а выражения типа (последнее действие — сложение) называются многочленами. В алгебре логики логическое умножение (конъюнкция) и логическое сложение (дизъюнкция) равноправны по своим свойствам. Поэтому выражения типа называются конъюнктивными одночленами, а выражения типа
называются не многочленами, а нормальными формами. На этом аналогия заканчивается. Далее вводятся понятия совершенных нормальных форм — дизъюнктивной и конъюнктивной.
Совершенные нормальные формы
Среди множества дизъюнктивных (равно как и конъюнктивных) нормальных форм, которыми обладает данная формула алгебры высказываний, существует уникальная форма: она единственна для данной формулы. Это так называемая совершенная дизъюнктивная нормальная форма (среди конъюнктивных форм — совершенная конъюнктивная нормальная форма ).
Определение 5.1. Одночлен (конъюнктивный или дизъюнктивный) от переменных называется совершенным, если в него от каждой пары входит только один представитель ( или ). Нормальная форма (дизъюнктивная или конъюнктивная) от переменных называется совершенной от этих переменных, если в нее входят лишь совершенные одночлены (конъюнктивные или дизъюнктивные соответственно) от .
Приведем пример совершенной конъюнктивной нормальной формы от четырех переменных
Вот несколько примеров совершенных дизъюнктивных нормальных форм:
Представление формул алгебры высказываний совершенными дизъюнктивными нормальными (СДН) формами
Введем обозначение, которое будет удобно в дальнейшем:
Легко проверить, что , т.е. , и (см. пояснения о значении формулы перед теоремой 2.2).
Введем еще одно обозначение. Вместо дизъюнкции будем писать . В частности, запись обозначает дизъюнкцию всевозможных выражений (формул) , зависящих от переменных , когда индексы суммирования (дизъюнктирования) ось пробегают всевозможные упорядоченные наборы длины
Лемма 5.2. Для всякой формулы алгебры высказываний справедливо разложение
Доказательство. Возьмем произвольный набор из нулей и единиц (каждое , где , есть либо 0, либо 1) и вычислим значения формул, стоящих в правой и левой частях доказываемой равносильности, при .
С одной стороны, в правой части доказываемого равенства получим
что представляет собой дизъюнкцию нескольких конъюнктивных одночленов. Каждый конъюнктивный одночлен характеризуется индексным набором нулей и единиц . Если для данного конъюнктивного одночлена набор нулей и единиц таков, что или , или , то согласно определению формулы , введенному в начале пункта, будем иметь или , или или . Но тогда и весь данный конъюнктивный одночлен будет равен нулю и потому на результат дизъюнкции влияния не окажет, а значит, из числа дизъюнктивных "слагаемых" может быть безболезненно исключен. Только один конъюнктивный одночлен окажется не равным нулю — тот, что характеризуется таким набором , который равен взятому в начале набору , т.е. для которого . Только для этого конъюнктивного одночлена будем иметь
Таким образом, конъюнктивный одночлен, соответствующий индексному набору , равен . Этому же значению равна и вся дизъюнкция, потому что, как показано выше, все остальные конъюнктивные одночлены равны нулю.
С другой стороны, формула, стоящая в левой части доказываемого равенства, обратится при в то же самое значение . Набор нулей и единиц был выбран произвольно. Следовательно, формулы в левой и правой частях равносильности действительно равносильны. Лемма доказана.
Представление формул алгебры высказываний совершенными дизъюнктивными нормальными формулами
Теорема 5.3 (о представлении формул алгебры высказываний совершенными дизъюнктивными нормальными формулами). Каждая не тождественно ложная формула алгебры высказываний от п аргументов имеет единственную (с точностью до перестановки дизъюнктивных членов) совершенную дизъюнктивную нормальную форму.
Доказательство. Существование. Всякая формула обладает указанным в предыдущей лемме разложением. Поскольку формула не тождественно ложна, то существуют такие наборы нулей и единиц, что . Наборы , обращающие формулу нулей и единиц, для которых . Тогда разложение для формулы
где дизъюнкция ("суммирование") ведется по всем индексным наборам нулей и единиц, для которых . Выражение, стоящее в правой части полученной равносильности, есть не что иное, как совершенная дизъюнктивная нормальная форма от переменных , потому что каждый конъюнктивный одночлен , входящий в дизъюнкцию, совершенен (каждая переменная входит в него точно один раз: либо сама, либо со знаком отрицания в зависимости от значения ее показателя степени).
Единственность. Предположим, что некоторая формула имеет два представления совершенными дизъюнктивными нормальными формами:
где , и , есть совершенные конъюнктивные одночлены от переменных . Причем, не нарушая общности, считаем, что ни один из одночленов не повторяется в этом наборе, потому что повторяющиеся одночлены можно исключить ввиду идемпотентности дизъюнкции (теорема 4.4, пункт ж)). Аналогична ситуация в форме . Тогда имеет место равносильность
Пусть, например, совершенный конъюнктивный одночлен имеет вид . Придадим переменным значения соответственно. Тогда совершенный конъюнктивный одночлен примет значение 1, и, следовательно, вся совершенная дизъюнктивная нормальная форма, стоящая в левой части равносильности, станет равна единице. Тогда и правая часть данной равносильности обратится в единицу, и для набора значений переменных одна из совершенных элементарных конъюнкций , например , также станет равной единице. Если имеет вид , то доказанное означает, что . Последнее равенство возможно в том и только в том случае, когда , что может быть лишь тогда и только тогда, когда . Следовательно, , т.е. . Таким образом, совершенная элементарная конъюнкция встречается среди совершенных элементарных конъюнкций . Тем же самым способом устанавливается, что любая из совершенных элементарных конъюнкций встречается среди , и обратно, любая из совершенных элементарных конъюнкций встречается среди . Ввиду того что одночлены в данных наборах не повторяются, то и обе части равносильности
отличаются самое большее порядком членов дизъюнкции.
Доказанная теорема — одна из важнейших в алгебре высказываний. Если вы до конца разобрали обе части доказательства (существование и единственность), то значит вы начали понимать категории и методы математической логики как математической науки. Доказательство существования состоит из двух частей: леммы и собственно теоремы. Доказательство единственности полностью содержится в теореме и не опирается на лемму.
Представление формул алгебры высказываний совершенными конъюнктивными нормальными (СКН) формами
Понятия и теоремы этого пункта носят двойственный характер по отношению к соответствующим понятиям и теоремам предыдущего пункта. Вводится следующее обозначение:
Легко проверяется, что , т.е. ; и .
Вместо конъюнкции будем писать . В частности, запись обозначает дизъюнкцию всевозможных выражений (формул) , зависящих от переменных , когда индексы произведения (конъюнктирования) пробегают всевозможные упорядоченные наборы длины
Аналогично доказательству леммы 5.2 доказывается лемма 5.4.
Лемма 5.4. Для всякой формулы алгебры высказываний справедливо разложение
Подобно теореме 5.3 выводится теорема 5.5.
Теорема 5.5 (о представлении формул алгебры высказываний совершенными конъюнктивными нормальными формами). Каждая формула алгебры высказываний от п переменных, не являющаяся тавтологией, имеет единственную (с точностью до перестановки конъюнктивных членов) совершенную конъюнктивную нормальную форму.
Доказательство этой теоремы можно восстановить, руководствуясь доказательством теоремы 5.3.
Два способа приведения формулы алгебры высказываний к совершенной нормальной форме
Эти два способа проистекают из двух способов задания формулы алгебры высказываний: с помощью таблицы ее значений или с помощью аналитической формы записи.
Если формула задана таблицей своих значений, то из доказательств теорем 5.3 и 5.5 о представлении формул совершенными нормальными формами необходимо вынести формулу (в некоем обычном понимании смысла этого термина) разложения формулы алгебры высказываний в совершенную нормальную форму. Для случая СДН-формы эта формула имеет следующий вид:
По сути, эта формула описывает правило (алгоритм) отыскания совершенной дизъюнктивной нормальной формы для данной формулы: нужно выбрать все те наборы значений ее переменных, на которых формула принимает значение 1; для каждого такого набора выписать совершенный конъюнктивный одночлен, принимающий значение 1 на этом наборе и только на нем; полученные совершенные конъюнктивные одночлены соединить знаками дизъюнкции. Для случая СКН-формы эта формула имеет вид
и, в свою очередь, описывает следующее правило (алгоритм) отыскания совершенной конъюнктивной нормальной формы для данной формулы: нужно выбрать все те наборы значений ее переменных, на которых формула принимает значение 0. Для каждого такого набора выписать совершенный дизъюнктивный одночлен, принимающий значение 0 на этом наборе и только на нем. Полученные совершенные дизъюнктивные одночлены соединить знаками конъюнкции.
Пример 5.6. Пусть, например, формула задана следующей таблицей своих значений:
Таким образом, она принимает значения 1 на следующих наборах значений своих переменных (или при следующих конкрети-зациях):
Запишем предыдущую формулу разложения в СДН-форму для случая
Пример 5.7. Для формулы из предыдущего примера найдем ее СКН-форму. Для этого сначала отметим все те наборы значений переменных, на которых она принимает значение 0: . Теперь запишем формулу разложения в СКН-форму для случая
Еще раз обращаем внимание на то, что для каждой формулы алгебры высказываний СДН-форма единственна и СКН-форма единственна (если они существуют). СДН-форма (5.1) отмечает все те наборы значений пропозициональных переменных, на которых данная формула принимает значение 1, а СКН-форма (5.2) отмечает все те наборы значений пропозициональных переменных, на которых данная формула принимает значение 0. Тем не менее необходимо отчетливо осознавать, что две полученные формулы (5.1) и (5.2) равносильны. Так, формула (5.1) принимает значение 0 на тех и только тех наборах значений переменных, на которых принимает значение 0 и формула (5.2). Аналогично формула (5.2) принимает значение 1 на тех и только тех наборах значений переменных, на которых принимает значение 1 формула (5.1).
Второй способ приведения формул алгебры высказываний к совершенной нормальной форме основан на равносильных преобразованиях данной формулы. В этом случае формула должна быть задана в аналитической форме. Для приведения формулы к совершенной нормальной форме нужно сначала привести ее к дизъюнктивной (или конъюнктивной) нормальной форме. Затем нужно продолжить равносильные преобразования полученных нормальных форм, с тем чтобы довести их до совершенства.
В заключение отметим, что одной из сфер применения нормальных форм является та, где требуется получить аналитическое выражение для формулы алгебры высказываний, которая задана своей таблицей значений (таблицей истинности), т.е. про которую известно, на каких наборах она принимает значение 0, а на каких — 1.
Теорема (о СДНФ). Для всякой не равной тождественному нулю формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СДНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки дизъюнктивных членов.
Определение. Совершенной конъюнктивной формулой формулы алгебры высказываний (СКНФ) называется КНФ, в которой:
1) различны все члены конъюнкции;
2) различны все члены каждой дизъюнкции;
3) ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной;
4) каждая дизъюнкция содержит все переменные, входящие в исходную формулу, т. е. имеет вид
где конъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=0.
Теорема (о СКНФ). Для всякой не равной тождественной единице формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СКНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки конъюнктивных членов.
Опишем два способа приведения к совершенным нормальным формам.
1-й способ – аналитический.
Приведение к СДНФ. Алгоритм приведения:
1) привести формулу с помощью равносильных преобразований к ДНФ;
2) удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);
3) из одинаковых членов дизъюнкции (если такие окажутся) удалить все, кроме одного;
4) из одинаковых членов каждой конъюнкции (если такие окажутся) удалить все, кроме одного;
5) если в какой-нибудь конъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член и применить закон дистрибутивности конъюнкции относительно дизъюнкции;
6) если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
7) Полученная формула и является СДНФ данной формулы.
Пример 27.
Привести следующие формулы к СДНФ с помощью равносильных преобразований:
Приведение к СКНФ. Алгоритм приведения:
1) привести формулу с помощью равносильных преобразований к КНФ;
2) удалить члены конъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);
3) из одинаковых членов конъюнкции (если такие окажутся) удалить все, кроме одного;
4) из одинаковых членов каждой дизъюнкции (если такие окажутся) удалить все, кроме одного;
5) если в какой-нибудь дизъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой дизъюнкции член и применить закон дистрибутивности дизъюнкции относительно конъюнкции;
1) если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
2) Полученная формула и является СКНФ данной формулы.
Пример 28.
Привести следующие формулы к СКНФ с помощью равносильных преобразований:
2-й способ – табличный.
Составляем таблицу истинности для данной функции.
Приведение к СДНФ. Алгоритм приведения.
Строим таблицу значений формулы. Рассматриваем только те строки, в которых значение формулы равно единице. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем, аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 – без отрицания. Наконец, образуем дизъюнкцию всех полученных конъюнкций.
Читайте также:

