Сообщение на тему звезды шум и логарифмы
Обновлено: 28.06.2024
Сопоставить цвета и звуки пытались еще в древние времена, когда физика, философия и эзотерика были не очень-то отделимы друг от друга. Ньютон, впервые получивший спектр в ходе экспериментов, изначально выделил в нем 5 цветных полос, потом - 9 (добавив промежуточные, переходные ступени), и только потом поддался всеобщей европейской любви к семерке (7 планет, 7 металлов, 7 дней недели и т.д.), чем предопределил массовое восприятие спектральных цветов на века вперед. Заодно и увязав цвета с семью нотами (на семиступенных ладах строилось тогда и строится поныне абсолютное большинство музыкальных композиций).
Видимая часть спектра между тем - штука непрерывная, и дробить ее на дискретные ступени каждый может в меру своей испорченности, ну то есть по возможностям и потребностям. Даже границы видимого диапазона нечеткие, различные источники дают цифры в 380-400 нм для коротковолнового края и 750-800 нм для длинноволнового, за которыми начинаются соответственно ультрафиолетовое (УФ) и инфракрасное (ИК) излучение. Нашел более-менее наглядную картинку - но помним, что ни один монитор даже в теории не способен передать чистые спектральные оттенки, цветовой охват не позволяет:

*место для остроумных оригинальных шуток о пропаганде ЛГБТ-символики*
Сразу обращает на себя внимание то, что длины волн, равно как и обратные им частоты, на границах спектра различаются ровно в два раза. Прямо как октава в музыке. Совпадение? Не думаю :-) Ну а поскольку мировым стандартом, который мне любовен и прельстив, стал 12-ступенный равномерно темперированный строй, в котором полутон означает отличие высот звуков в 2^(1/12) раз (примерно на 5,9463%) - так воспользуемся же им. А совпадение разброса значений длин волны в нанометрах и соответствующих частот в терагерцах наводит на мысль о красивом выборе точки отсчета - там, где они совпадают и равны корню из 299792,458 - надеюсь, не надо объяснять, что это за число и почему. Границы при этом оказались равными 387 и 774 (что ТГц, что нм) - вполне себе.
Обозначения цветов для основной части диапазона легли как родные. Только вот красная часть спектра оказалась очень длинной, не стал экспериментировать с подбором названий оттенков для более глубоких (длинноволновых) точек - отсылаться к видимой их темности не очень-то корректно, это другая ось. Пришлось просто пронумеровать (с учетом того, что максимально "естественный" красный - наиболее коротковолновый среди них). Отсчет нот ничтоже сумняшеся начал с "ля" (A) - камертон все-таки - и не прогадал: классическая триада RGB (красный - зеленый - синий) оказалась. аккордом до-мажор! (Ноты мажорного трезвучия соотносятся по высоте как 4:5:6).
Звезды, шум и логарифмы 2.0 (кто понял, тот понял)
Кстати, о четвертях - наблюдение. Существует три достаточно популярных единицы измерения логарифмического характера, применяемые для явлений, описываемых законом Вебера-Фехнера (интенсивность ощущения пропорциональна логарифму раздражения, то есть увеличение абсолютного показателя В какое-то число раз, геометрически, соответствует перемещению НА какое-то количество единиц шкалы, арифметически):
1) Вышеупомянутые полутона в музыке. 1 полутон = увеличение высоты звука в ~1,059463 раз (12 полутонов - ровно в 2 раза);
2) Децибелы (или более общее - децилоги). 1 децибел = увеличение интенсивности (громкости) звука в 10^0,1 = ~1,258925 раз (1 бел = 10 дБ - ровно в 10 раз);
3) Звездные величины (магнитуды). Единица шкалы звездных величин = изменение наблюдаемой яркости (светимости) небесных тел в 10^0,4 = ~2,511886 раз (5 единиц - ровно в 100 раз).
Так вот - каждая из последующих единиц в 4 раза больше предыдущей! В случае с децибелами и магнитудами - математически точно, с полутонами и децибелами - с малой погрешностью, вызванной разницей между значениями 2^(1/3) = ~1,259921 и 10^0,1 (см. пост об оптимальной шкале масштабов). И при этом пороги различимости для каждой из величин - как раз в районе четверти от выбранных единиц. И кстати, полутона и децибелы технари могут увидеть в рядах предпочтительных чисел R40 и R10.
В связи с чем интересно, для какого явления применима еще в 4 раза более грубая шкала, чем звездные величины, а именно - с единицей, соответствующей росту показателя в 40 раз (что примерно равно 10^1,6).
2. Звёзды, шум и логарифмы. Этот заголовок связывает, столь казалось бы, несоедимые вещи. Шум и звёзды объединяются здесь потому, что громкость шума и яркость звёзд оцениваются одинаковым образом: По логарифмической шкале. Астрономы делят звезды по степени яркости на видимые абсолютные звездные величины; Звезды первой величины, второй и третьей и т.п. Последовательность видимых звездных величин, которые воспринимались глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону:
Алгебра 11 класс
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Презентация на тему: Математические Логарифмы в Астрономии. ГБПОУ "ВТНиГМ им. Н. Сердюкова" Выполнили: Бригада №1. Волгоград 2017

Содержание: 1.Определение. 2.Логарифмы и звезды. 3.Проблемы и открытие логарифмов. 4.Ученые открыватели. 5.Звездные величины. 6.Шкала звездных величин. 7.Вывод.

Определение ОПРЕДЕЛЕНИЕ Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. a logab = b

Логарифмы и звезды. По логарифмической шкале. Астрономы делят звезды по степени яркости на видимые абсолютные звездные величины. Звезды первой величины, второй и третьей и т.п. Последовательность видимых звездных величин, которые воспринимались глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону. Звёзды, шум и логарифмы. Этот заголовок связывает, столь казалось бы, несоединимые вещи. Шум и звёзды объединяются здесь потому, что громкость шума и яркость звёзд оцениваются одинаковым образом:


Проблемы и открытие логарифмов В течение ХVI в. резко возрос объем работы, связанный с проведением приближенных вычислений в ходе решения разных задач, и в первую очередь задач астрономии, имеющей непосредственное практическое применение Наибольшие проблемы возникали при выполнения операций умножения и деления. Попытки частичного упрощения этих операций путем сведения их к сложению большого успеха не приносили. Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов, удлинило по выражению Лапласа, жизнь вычислителей.

Ученые открыватели Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, - резко повысившее производительность труда вычислителей. Добавим, что уже в 1623 г., т.е. всего через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений. Первые таблицы логарифмов составлены независимо друг от друга И. Бюрги и Дж. Непером и. В таблицы вошли значения логарифмов синусов косинусов и тангенсов для углов от 0 до 900 градусов.



Шкала звездных величин Шкала звездных величин сохранилась и уточнена. Блеск звезды 1т больше звезды в 6т ровно в 100 раз. Следовательно, разность в 5 звездных величин соответствует различию в блеске ровно в 100 раз. Обозначим через х число, показывающее различие в блеске в одну звездную величину, тогда x5 = 100. Найдем значение х из этого равенства: 5 lg x = lg 100, отсюда 5 lg x = 2 или lg x = 0,4, тогда х = 2, 512. Если обозначить блеск звезды, звездная величина которой равна m1, через I1, а блеск звезды, звездная величина которой равна m2, через I2, то L`1 / L`2 = 2,512 (m2 – m1)

Вывод: 1.Логарифмы имеют прикладное значение в астрономии. 2.Изобретение логарифмов сократило и упростило работу астронома.
4 Введение В течение ХVI в. резко возрос объем работы, связанный с проведением приближенных вычислений в ходе решения разных задач, и в первую очередь задач астрономии, имеющей непосредственное практическое применение (при определения положения судов по звездам и по Солнцу). Наибольшие проблемы возникали при выполнения операций умножения и деления. Попытки частичного упрощения этих операций путем сведения их к сложению большого успеха не приносили. Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов, удлинило по выражению Лапласа, жизнь вычислителей.
5 Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, - резко повысившее производительность труда вычислителей. Добавим, что уже в 1623 г., т.е. всего через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений. Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером ( ) и швейцарцем И. Бюрги ( ). В таблицы Непера вошли значения логарифмов синусов, косинусов и тангенсов для углов от 0 до 900 с шагом в 1 минуту. Бюрги подготовил свои таблицы логарифмов чисел, но вышли в свет они в 1620 г., уже после издания таблиц Непера, и поэтому остались незамечеными.
6 2. Звёзды, шум и логарифмы. Этот заголовок связывает, столь казалось бы, несоедимые вещи. Шум и звёзды объединяются здесь потому, что громкость шума и яркость звёзд оцениваются одинаковым образом: По логарифмической шкале. Астрономы делят звезды по степени яркости на видимые абсолютные звездные величины; Звезды первой величины, второй и третьей и т.п. Последовательность видимых звездных величин, которые воспринимались глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону:
9 Пример: Тихий шелест листьев оценивается в 1 бел, громкая разговорная речь – в 6,5 бела, рычание льва – в 8,7 бела. Отсюда следует, что по силе звука разговорная речь превышает шелест листьев в 10 6,5 – 1 = 10 5,5 = раз; львиное рычание сильнее громкой разговорной речи в 10 8,7 – 6,5 = 10 2,2 = 158 раз.
12 Шкала звездных величин сохранилась и уточнена. Блеск звезды 1 т больше звезды в 6 т ровно в 100 раз. Следовательно, разность в 5 звездных величин соответствует различию в блеске ровно в 100 раз. Обозначим через х число, показывающее различие в блеске в одну звездную величину, тогда x 5 = 100. Найдем значение х из этого равенства: 5 lg x = lg 100, отсюда 5 lg x = 2 или lg x = 0,4, тогда х = 2, 512. Если обозначить блеск звезды, звездная величина которой равна m 1, через I 1, а блеск звезды, звездная величина которой равна m 2, через I 2, то L` 1 / L` 2 = 2,512 (m 2 – m 1 )
13 Нулевые и отрицательные звездные величины Светила, блеск которых превосходит блеск звезды 1 т, имеют нулевые и отрицательные звездные величины (0 т, -1 т и т.д.). К ним относятся несколько наиболее ярких звезд и планет, а также конечно, Солнце и Луна. Шкала звездных величин продолжается и в сторону звезд, не видимых невооруженным глазом. Есть звезды 7 т, 8 т и т.д. Для более точной оценке блеска звезд используются дробные звездные величины 2,3 т ; 7,1 т ; 6,2 т ; 14,5 т ; и т.д.
14 Например: Во сколько раз Капелла ярче Денеба? Из таблицы найдем звездную величину Капеллы (m 1 = +0,2 т ) и Денеба (m 2 = +1,3 т ). Задача:Дано:Решение: m 1 = +0,2 т I 1 /I 2 = 2,512 (т2-т1) m 2 = +1,3 т lg I 1 /I 2 = (m 2 -m 1 ) lg 2,512 = 0,4; то для Капеллы и Денеба: I 1 /I 2 - ?Lg I 1 /I 2 = 0,4 * 1,1 = 0,44; I 1 / I 2 = 2,75. Ответ: I 1 /I 2 = 2,75.
16 ОПРЕДЕЛЕНИЕ Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.b. a log a b = b


Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.
Джон Непер (1550—1617)
Йост Бюрги (1552—1632)
Между математикой и музыкой существуют многообразные связи. Они сложились исторически благодаря глубокой внутренней необходимости, которую можно объяснить тем, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства. Эту связь не раз подчеркивали и математики, и музыканты.

Логарифм и восприятие звука
Когда мы слышим игру музыкальных инструментов или пение артиста, мы не задумываемся о природе звука, положенного в основу любого музыкального действия. Существует наука – музыкальная акустика, объединяющая физику, музыку и математику.
Тон – важное понятие акустики, представляет собой непосредственное восприятие колебаний, возникающих при звучании струны, голоса.
Логарифмическая спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию.


Сила звука – это количество звуковой энергии, проходящей через единицу поверхности в единицу времени. Эта физическая величина, как это ни странно выглядит, не выражает величины нашего звукового ощущения – громкости. Мы стали слушать звуки различных частот, но одинаковой силы, они показались нам отличающимися по громкости. Мы заинтересовались этим. Такое явление объясняется разной чувствительностью нашего уха к звукам различной частоты .

Мы провели эксперимент, стали увеличивать силу звука в 2, 3, 4 раза, оказалось, что наше звуковое ощущение (громкость звука) во столько же раз не увеличивается.
В 1846 физиолог Вебер установил зависимость между ощущением и раздражением, вызывающим это ощущение. В 1860 году ученый Фехнер подверг закон Вебера математической обработке, согласно которому ощущение изменяется пропорционально логарифму раздражения: это видно из формулы
– последующее раздражение, k – коэффициент пропорциональности.
Действительно, при увеличении силы звука в 100, 1000 и т. д. раз ощущение увеличивается в 2, 3 и т. д. раза (при k = 1).
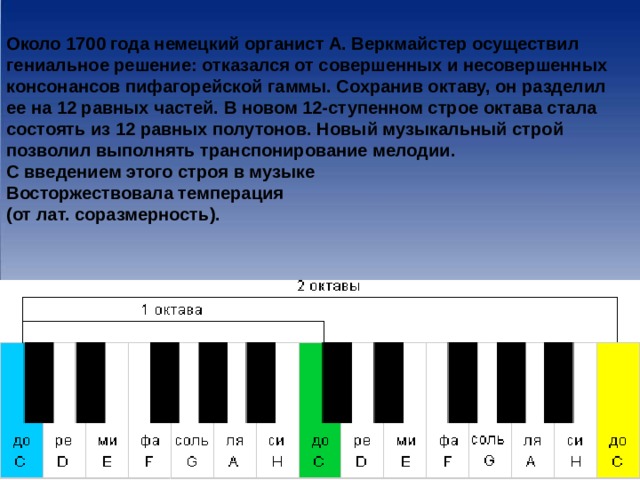
Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы. Сохранив октаву, он разделил ее на 12 равных частей. В новом 12-ступенном строе октава стала состоять из 12 равных полутонов . Новый музыкальный строй позволил выполнять транспонирование мелодии.
С введением этого строя в музыке
Восторжествовала темперация
(от лат. соразмерность).


Положим, что ноте “до” самой низкой октавы – будем ее называть нулевой – соответствует частота, равная п колебаниям в секунду. В октаве частота колебаний нижнего звука в 2 раза меньше верхнего, т.е. эти частоты соотносятся как 1 : 2. Тогда ноте “до” первой октавы будут соответствовать 2 п колебаний в сек., а ноте “до” третьей октавы - 2 m · п колебаний в сек. И так далее. Тогда высоту, т.е. частоту любого звука можно выразить формулой
N mn = n · 2 ( 12 v2) p
Логарифмируя эту формулу получаем:
lg N mp = lg n + m lg2 + p(lg2)/12,
lg N mp = lg n + (m + p/12) lg2
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2, имеем log 2 N mp = Севастьян Бах Прелюдия Фуга “до – минор”.
Читайте также:

