Сообщение на тему высказывания логической операции
Обновлено: 05.07.2024
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A↖$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.

Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.

Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.

Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ ∧B) ∧ (A ∧ B↖)$ |
| Импликация | А → В | $A↖ ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ ∧ B↖) ∨ (A ∧ B)$ |
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X 3) ∨ (1 3) ∨ (12 3) ∨ (3 2) → (X > 5)) .
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a - π/b) a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы $↖ ∧ X2 ∨ ↖ ∨ X1$.
| X1 | X2 | $↖$ | $↖$ \ X2 | X1 ∧ X2 | $↖$ | $↖$ ∧ X2 ∨ $↖$ | $↖$ ∧ X2 ∨ $↖$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ $↖$ ∧ $↖$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ $↖$ ∧ $↖$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ $↖$ ∧ $↖$ ∨ X2 = X1 ∧ $↖$ ∨ X1 ∧ X2 ∨ $↖$ ∧ $↖$ ∨ $↖$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $↖$ ∧ $↖$ ∨ 0 = X1 ∧ X2 ∨ $↖$ ∧ $↖$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $↖$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ $↖$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ $↖$ ∧ X2 = X2 ∧ (X1 ∨ $↖$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | $↖$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ $↖$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ $↖$ ∧ $↖$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∪ X1 ∧ $↖$ ∧ $↖$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∨ X1 ∧ $↖$ ∧ $↖$ = X2 ∧ X3 ∧ (X1 ∨ $↖$) ∨ X1 ∧ $↖$ ∧ (X2 ∨ $↖$) = X2 ∧ X3 ∨ X1 ∧ $↖$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее' высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Примеры высказываний:
1. Москва – столица России.
2. Число 27 является простым.
3. Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27 = 3*3*3.
Следующие предложения высказываниями не являются:
- Давай пойдем гулять.
- 2*x > 8.
- a*x2 + b*x + c = 0.
- Который час?
Отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примеры высказываний:
1. Сегодня светит солнце.
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0.
Простые высказывания назвали логическими переменными, а сложные - логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
| Истина | И | True | T |
| Ложь | Л | False | F |
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Логическое выражение - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Связки "НЕ", "И", "ИЛИ" заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции , при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
Конъюнкция - логическое умножение (от латинского conjunctio - союз, связь):
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Если два высказывания соединены союзом "И", то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция - логическое сложение (от латинского disjunctio - разобщение, различие):
Дизъюнкция - это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Если два высказывания соединены союзом "ИЛИ", то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание.
Инверсия - отрицание (от латинского disjunctio - разобщение, различие):
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
Если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация):
A => B
"Из А следует В"
Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) - истинно, а следствие (заключение В) - ложно и истинно во всех остальных случаях.
A B
"А равносильно В"
Новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
| Логическая связка | Название логической операции | Обозначения |
| не | Отрицание, инверсия | Ø, ù |
| и, а, но | Конъюнкция, логическое умножение | &, • , Ù |
| или | Дизъюнкция, логическое сложение | V, + |
| если . то | Импликация, следование | Þ,® |
| тогда и только тогда, когда | эквивалентность, эквиваленция, равнозначность | Û, ~, º, « |
Примеры записи сложных высказываний с помощью обозначения логических связок:
1. "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V A В
2. "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А => В
Построение таблиц истинности и логических функций
Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.
Порядок выполнения логических операций в сложном логическом выражении:
Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
количество строк = 2 n + строка для заголовка,
n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
- определить количество переменных (простых выражений);
- определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.
Пример: Составить таблицу истинности логического выражения:
D = А & (B Ú C).
1. Определить количество строк:
на входе три простых высказывания: А, В, С поэтому n = 3 и количество строк = 2 3 +1 = 9.
2. Определить количество столбцов:
- простые выражения (переменные): А, В, С;
- промежуточные результаты (логические операции):
А - инверсия (обозначим через E);
B Ú C - операция дизъюнкции (обозначим через F);
а также искомое окончательное значение арифметического выражения:
D = А & (B Ú C). т.е. D = E & F - это операция конъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций.
| A | B | C | E | F | E & F |
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции:
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
1. Выделить в таблице истинности те строки, в которых значение функции равно 1.
2. Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
4. Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
1. В первой и третьей строках таблицы истинности значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции запишим в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию:
Z (X, Y) =( X & Y) V (X & Y).
Законы логики и правила преобразования логических выражений
1. Закон двойного отрицания (двойное отрицание исключает отрицание):
А = .
2. Переместительный (коммутативный) закон:
- для логического сложения: А Ú B = B Ú A;
- для логического умножения: A & B = B & A.
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
3. Сочетательный (ассоциативный) закон:
- для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);
- для логического умножения: (A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
- для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C).
Закон определяет правило выноса общего высказывания за скобку.
- для логического сложения: = & ;
- для логического умножения: = Ú
6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
- для логического сложения: А Ú A = A;
- для логического умножения: A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
- для логического сложения: А Ú 1 = 1, А Ú 0 = A;
- для логического умножения: A & 1 = A, A & 0 = 0.
- A & = 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
- для логического умножения: A & (A Ú B) = A.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Упрощение формул.
Пример 1. Упростить формулу (А Ú В) & (А Ú С).
4. Аналогично предыдущему пункту вынесем за скобки высказывание А. A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности.
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
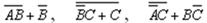
Пример 2. Упростить выражения так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
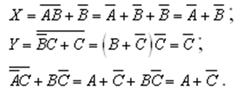
Решение :
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Высказывания в алгебре логики и логические операции над ними
Элементами логических рассуждений являются высказывания.
Простое высказывание – это повествовательное предложение, которое или истинно, или ложно.
Число 100 делится на 25 без остатка (истинно).
Рим – столица Франции (ложно).
Вопросительные и восклицательные предложения не являются высказываниями. Простые высказывания обозначаются заглавными буквами латинского алфавита.
Действия логических операций задаются таблицами истинности.
Эти таблицы содержит все комбинации значений истинности простых высказываний, и для каждой такой комбинации указывается значение истинности сложного высказывания.
К основным логическим операциям над высказываниями относятся: отрицание, дизъюнкция, конъюнкция, импликация, сложение по модулю 2, эквивалентность, стрелка Пирса, штрих Шеффера.
Когда высказывание А истинно, то ложно; когда А ложно, истинно.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Выделяют следующие логические операции: инверсия; конъюнкция; дизъюнкция; импликация; эквиваленция.
1. Операция инверсия (отрицание):
Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Обозначается:
В естественном языке: соответствует словам "неверно, что. " и частице "не"
Диаграмма Эйлера-Венна:

Принимаемые значения:
Диаграмма Эйлера-Венна:
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.


Пример: Луна — спутник Земли (А) . Луна — не спутник Земли ( A)
2. Операция конъюнкция (лат. conjunctio — соединение) (логическое умножение):
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначается:
В естественном языке: соответствует союзу "и"

Принимаемые значения:
Диаграмма Эйлера-Венна:
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.


1. 10 делится на 2 (A - и) . 5 больше 3 (B - и) . 10 делится на 2 и 5 больше 3 (A B - и) .

2. 10 не делится на 2 (A - л) . 5 больше 3 (B - и) . 10 не делится на 2 и 5 больше 3 (A B - л) .

3. 10 делится на 2 (A - и) . 5 не больше 3 (B - л) . 10 делится на 2 и 5 не больше 3 (A B - л) .

4. 10 не делится на 2 (A - л) . 5 не больше 3 (B - л) . 10 делится на 2 и 5 больше 3 (A B - л) .
3. Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):
Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Обозначается:
В естественном языке: соответствует союзу "или"

Принимаемые значения:
Диаграмма Эйлера-Венна:
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.


1. 10 делится на 2 (A - и) . 5 больше 3 (B - и) . 10 делится на 2 или 5 больше 3 (A B - и) .

2. 10 не делится на 2 (A - л) . 5 больше 3 (B - и) . 10 не делится на 2 или 5 больше 3 (A B - и) .

3. 10 делится на 2 (A - и) . 5 не больше 3 (B - л) . 10 делится на 2 или 5 не больше 3 (A B - и) .

4. 10 не делится на 2 (A - л) . 5 не больше 3 (B - л) . 10 не делится на 2 или 5 не больше 3 (A B - л) .
4. Операция импликация (лат. лат. implico — тесно связаны) (логическое сложение):
Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Обозначается: о
В естественном языке: соответствует обороту "если . то . "

Принимаемые значения: л

1. Данный четырёхугольник — квадрат (A - и) . Около данного четырёхугольника можно описать окружность (B - и) . Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - и) .

2. Данный четырёхугольник — не квадрат (A - л) . Около данного четырёхугольника можно описать окружность (B - и) . Если данный четырёхугольник не квадрат, то около него можно описать окружность (A B - и) .

3. Данный четырёхугольник — квадрат (A - и) . Около данного четырёхугольника нельзя описать окружность (B - л) . Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - л) .

4. Данный четырёхугольник — не квадрат (A - л) . Около данного четырёхугольника нельзя описать окружность (B - л) . Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A B - и) .
5. Операция эквиваленция (двойная импликация):
Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Обозначается: о
В естественном языке: соответствует оборотам речи "тогда и только тогда" ; "в том и только в том случае"

Принимаемые значения:

1. 24 делится на 6 (A - и) . 24 делится на 3 (B - и) . 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - и) .

2. 24 не делится на 6 (A - л) . 24 делится на 3 (B - и) . 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л) .

3. 24 делится на 6 (A - и) . 24 не делится на 3 (B - л) . 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л) .

4. 24 не делится на 6 (A - л) . 24 не делится на 3 (B - л) . 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A B - и) .
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация и эквиваленция.
Логические формулы.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
1. Всякая логическая переменная и символы "истина" ("1" ) и "ложь" ("0" ) — формулы.
2. Если А и В — формулы, то , (А &В) , (А v В) , (А B) , (А В) — формулы.
3. Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
Рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" .
Обозначим буквой A высказывание: "купить яблоки" , буквой B - высказывание: "купить абрикосы" , буквой C - высказывание: "испечь пирог".
Тогда высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" формализуется в виде формулы:

(A v B) C
Формула выполнимая - если при определенных сочетаниях значений переменных она принимает значение "истина" ("1" ) или "ложь" ("0" ).

Как показывает анализ формулы (A v B) C , при определённых сочетаниях значений переменных A , B и C она принимает значение "истина" , а при некоторых других сочетаниях — значение "ложь" .

Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v A , соответствующая высказыванию “Этот треугольник прямоугольный или косоугольный” . Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный.
Тавтология - тождественно истинная формула, или формула принимающая значение "истина" ("1" ) при любых входящих в нее значениях переменных.
Логически истинные высказывания - высказывания, которые формализуются тавтологиями.
В качестве другого примера рассмотрим формулу А & A , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати” . Очевидно, что эта формула ложна, так как либо А , либо A обязательно ложно.
Противоречие - тождественно ложная формула, или формула принимающая значение "ложь" ("0" ) при любых входящих в нее значениях переменных.
Логически ложные высказывания - высказывания, которые формализуются противоречиями.
Равносильные формулы - две формулы А и В принимающие одинаковые значения, при одинаковых наборах значений входящих в них переменных.

Равносильность двух формул алгебры логики обозначается символом .
Равносильное преобразование формулы - замена формулы другой, ей равносильной.
Читайте также:

