Сообщение на тему трисекция угла
Обновлено: 05.07.2024
Уже давно известно, и я писал об этом на своём канале, что данная задача для произвольного угла неразрешима с помощью только лишь циркуля и линейки.
Так в чем же "хитрость" Архимеда? А дело в том, что древнегреческий гений смог решить эту задачу, просто нанеся на линейку две насечки . Посмотрим же, каким образом он провернул эту "аферу".
Трисекция произвольного угла
Итак, имеется произвольный угол, который необходимо разделить на трое:
Берем в руки циркуль и проводит окружность произвольного радиуса с центром в вершине угла:
Так же мы продолжили одну из сторон угла влево. Теперь берем в руки линейку и ставим на ней две засечки так, чтобы расстояние между ними было равно радиусу окружности:
Самая главная "хитрость" будет заключаться в том, что найти такое положение линейки, при котором она будет:
- проходить через точку А;
- первая насечка будет лежать на окружности;
- вторая насечка будет лежать на продолжении стороны угла.
Выглядит это следующим образом:
Собственно говоря, построение закончено! Осталось лишь доказать, что угол, который мы построили действительно ровно в три раза меньше исходного.
Итак, взглянем на рисунок:
Треугольник BCO - равнобедренный (ведь мы же специально так сделали насечки!) Остальное - просто и понятно: пользуемся тем, что сумма углов треугольника и величина развернутого угла равны 180 градусам.
Делаем окончательный вывод:
Изображенное выше построение с помощью линейки с засечками у древних греков называлось методом "невсиса" (от слова "наклон"). Невсис считался менее респектабельным методом решения задач, чем классические циркуль и линейка, и его применение с течением времени сошло на нет.
Кстати, невсис позволяет решать и другие великие задачи древности , например:
Впервые мысль о делении угла на три равные части с помощью циркуля и линейки возникла в V в. до новой эры в умах древнегреческих строителей и архитекторов, которым, по некоторым свидетельствам, удалось построить трисектрису прямого и острого углов, хотя с уменьшением угла уменьшалась и точность построения. Архимед, задавшись той же целью, придумал новый способ решения этой задачи: правда, для этого ему пришлось использовать не совсем обычную линейку, а снабженную двумя специальными метками — засечками. Его способ, не отличающийся простотой и точностью, не позволил, тем не менее, поделить на три равные части тупой угол — он, в отличие от прочих, все же не поддался усилиям этого ученого. Несмотря на то, что условием решения задачи было обязательное использование исключительно линейки и циркуля, математик Гиппий Элидский рискнул применить изобретенную им кривую — квадратрису Динострата, благодаря точности которой им была построена и более совершенная трисектриса. Папп Александрийский, наравне с традиционными инструментами, применил конхоиду Никомеда, которая, как этого ни добивался ученый, не добавила трисекции точности.
С течением времени, потраченного математиками разных стран на решение этой задачи, было выявлено, что разделить угол на три равные части только с помощью циркуля и линейки без засечек (без применения специальных инструментов: улитки Паскаля, спирали Архимеда, известных уже квадратрисы и конхоиды Никоменда) невозможно. Это предположение возникло в голове у Р.Декарта, а французский математик П. Ванцель в 1837 году научно доказал его справедливость.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Сама жизнь требовала от геометров хорошо разработанной теории и практики построения правильных многоугольников. Строить правильные многоугольники сравнительно просто, когда равные дуги получались делением соответствующих равных центральных углов пополам. И возникали чрезвычайно большие трудности, когда необходимо было получить равные дуги при делении центрального угла на три равные части, тогда перед геометрами возникли чрезвычайно большие трудности, которые привели ученых к специальному рассмотрению задачи о трисекции угла.
Цель исследования – изучение и экспериментальная проверка теоретических основ возможностей построения трисекции угла.
Объект исследования – процесс построения трисекции угла.
Предмет исследования – методы построения трисекции угла.
Проблема исследования заключается в выявлении условий, при которых возможно построение трисекции угла с помощью циркуля и линейки, а при которых невозможно.
Задачи исследования – в соответствии с целью и проблемой исследования я поставил следующие задачи:
Изучить развитие идей построения трисекции угла;
Определить условия разрешимости задачи о трисекции угла с помощью циркуля и линейки;
Изучить теоретические основы неразрешимости задачи о трисекции угла с помощью циркуля и линейки;
Изучить геометрические построения трисекции угла с помощью других средств;
Найти практическое применение данной задачи;
Изготовить прибор для выполнения трисекции угла;
Изучить самостоятельно основные формулы тригонометрии.
Методы исследования: сбор, изучение, анализ, обобщение экспериментального и теоретического материала, рефлексивное осмысливание результатов построения выбранными методами.
2.1.Задача: построить трисектрису 1 данного угла.
Известна следующая легенда. Один пифагореец умирал на чужбине и не мог заплатить человеку, который за ним ухаживал. Перед смертью он велел ему изобразить на своем жилище пятиконечную звезду (она была их опознавательным знаком и символизировала здоровье): если когда-нибудь мимо будет идти пифагореец, он обязательно спросит о ней. И действительно, несколько лет спустя некий пифагореец увидел этот знак и вознаградил хозяина дома.
Но мне кажется , что при составлении рабочих чертежей орнаментов, разного рода украшений, многогранных колоннад и т.д., при строительстве, внутренней и внешней отделке храмов, надгробных памятников и других больших и малых сооружений древние инженеры, художники и архитекторы встретились с необходимостью уметь делить окружность на любое конечное число равных частей, а это довольно часто приводило их к рассмотрению трисекции некоторых углов. Делить угол пополам древние греки умели довольно легко, а вот разделить угол на три равные части оказалось не всегда возможно.
2.2. Углы, трисекция которых выполнима с помощью циркуля и линейки.

Ниже я привел подробное описание построения трисекции угла в 90°. Можно легко указать бесчисленное множество углов, для которых трисекция выполнима с помощью циркуля и линейки. Можно, например, с таким же успехом разделить угол в 45° на три равные части (Приложение №1). Вообще, трисекция выполнима для углов вида /2 n , где n - целое положительное число.
Пусть дан прямой угол ABC (рис.1) и требуется разделить его на три равные части, т.е. произвести трисекцию этого угла. Для этого из вершины данного угла B , как из центра, проводим окружность (для нужного построения достаточно четверть окружности). Точки пересечения окружности со сторонами AB и BC соответственно обозначим через M и N . Далее, из точек М и N тем же радиусом делаем засечки R и Q . Теперь соединим хордами М и R , N и Q . Получаем два равносторонних треугольника: Δ В R М и Δ В QN . Но в равностороннем треугольнике все три угла по 60°. Следовательно, МВ R = Q ВN = 60°. Тогда МВ Q = R ВN= Q В R = 30°. Итак, данный прямой угол удалось разделить на три равные части. Что и нужно было сделать.
2.3. Доказательство неразрешимости трисекции угла
с помощью циркуля и линейки в общем виде
Обозначу данный угол, который нужно разделить на три равные части, через 3 . Рассмотрю cos 3 .
По известным формулам тригонометрии буду иметь:
cos 3 = cos ( +2 ) = cos cos 2 - sin sin 2 = cos (cos 2 - sin 2 ) - sin 2sin cos =
=cos 3 - cos sin 2 - 2sin 2 cos = cos 3 - 3cos (1 - cos 2 ) = cos 3 - 3cos + 3cos 3 =
Итак , cos 3 = 4cos 3 - 3cos . Умножая левую и правую части уравнения на 2, получу , 2 cos 3 = 8 cos 3 - 6 cos . Пусть теперь 2 cos 3 = a , а 2 cos = x , тогда a = x 3 – 3 x ;
Когда это уравнение для некоторого а разрешимо в квадратных радикалах, то трисекция соответствующего угла выполнима при помощи циркуля и линейки, и наоборот: если для данного угла выполнима трисекция, то соответствующее уравнение должно быть разрешимо в квадратных радикалах.
Чтобы доказать, что трисекция угла не разрешима в общем виде, достаточно указать хотя бы один угол, который нельзя разделить при помощи линейки и циркуля на три равные части. Предположим, что 3 =60°, тогда cos 3 =0.5, и уравнение примет вид:
В алгебре доказывается, что рациональными корнями уравнения могли бы быть +1 и -1, но ни то, ни другое указанному уравнению не удовлетворяет.
Таким образом угол в 60° не может быть разделен на три части с помощью циркуля и линейки; угол в 20° (а следовательно, и угол в 40°) не может быть построен с помощью этих средств решения.
При решении задачи трисекции угла можно ограничиться случаем острого угла, потому что если >90°, то /3 = ( — 90°)/3 + 30°, а угол 30° легко построить циркулем и линейкой.
2.4. Методы решения задачи о трисекции угла
Изучая различную литературу, я старался найти как можно больше решений задачи о трисекции угла. Вот эти решения с их полным описанием.
Возьмем на стороне угла с вершиной В произвольную точку А и опустим из нее перпендикуляр АС на другую сторону (рис. 2). Проведем через точку А луч , сонаправленный с лучом ВС. Вставим теперь между лучами АС и отрезок DE длиной 2АВ так, чтобы его продолжение проходило через точку В. Тогда ЕВС= ABC /3. В самом деле, пусть G — середина отрезка DE . Точка А лежит на окружности с диаметром DE , поэтому AG = GE = AB = DE /2. Треугольники BAG и AGE равнобедренные, поэтому ABG = AGB =2 AEG =2 EBC , CBE = ABC /3
2.4.2. Решение Архимеда
2.4.3. Решение Гиппия при помощи открытой им квадратрисы
Квадратриса – плоска я трансцендентная прямая, определяемая кинематически.
Трансцендентные прямые – аналитические кривые, не являющиеся алгебраическими, т.е. для которых функция F ( x ; y ) есть многочлен от двух переменных.

Квадратриса получается следующим образом. Рассмотрим квадрат ABCD. Пусть концы отрезка ВС равномерно движутся по прямым ВА и CD, а отрезок АВ равномерно вращается вокруг точки А, причем в положение AD оба отрезка приходят одновременно (рис. 4). Пусть, далее, в некоторый момент отрезок ВС переместился в положение В`С`, а отрезок АВ переместился в положение AN; L — точка пересечения отрезков В`С` и AN. Гиппий рассмотрел кривую, состоящую из всех точек L. Чтобы получить треть угла NAD, опустим из точки L перпендикуляр LH на прямую AD и разделим отрезок LH точкой Р в отношении 1:2. Пусть Q — такая точка квадратрисы, что PQ BC. Из определения квадратрисы следует, что LAQ: QAK=LP:PH=1:2 , т. е. AQ — искомый луч и LAQ= LAK/3.
2.4.4. Решение при помощи спирали Архимеда
Архимедова спираль — спираль , плоская кривая, траектория точки L (рис. 5), которая равномерно движется вдоль луча OA с началом в O , в то время как сам луч OA равномерно вращается вокруг O .

Эта кривая получается следующим образом. Пусть луч ОА равномерно вращается вокруг точки О, а точка L равномерно движется по этому лучу, причем в начальном положении она находится в точке О (рис. 5). Тогда точка L движется по спирали Архимеда. Пусть угол АОВ нужно разделить в заданном отношении. Рассмотрим часть спирали Архимеда, полученную при вращении луча от начального положения ОА до положения ОВ. Пусть Р—точка, которая делит OL в отношении 1:2, где L — точка пересечения луча ОВ и спирали, Q — точка пересечения спирали и окружности радиуса ОР с центром О. Из определения спирали следует, что LOQ : QOA = LP : QO = LP : PO = 1:2, т. е. OQ —искомый луч и LOQ = BOA /3
2.4.5. Решение при помощи улитки Паскаля

В
озьмем на окружности радиуса R точку А и проведем через нее прямую . Прямая пересекает окружность в точках X и А (если —касательная, то Х=А). Пусть М 1 и М 2 — такие точки прямой , что ХМ 1 = ХМ 2 = а, где а — фиксированное число. Множество всех точек М 1 и М 2 (для всех прямых ) называют улиткой Паскаля .
Нас будет интересовать случай, когда a = R (рис. 6). Пусть векторы XM 1 и АХ сонаправлены, В—точка на продолжении отрезка М 1 О за точку О. Так как треугольники M 1 XO и ХОА равнобедренные, то OAX =2 OM 1 A и AOB = OM 1 A + OAX = = 3 OM 1 A . Поэтому для трисекции угла , где 0 /2, можно поступить следующим образом. Возьмем точку В так, что АОВ = . Пусть прямая ОВ пересекает сплошную часть улитки Паскаля в точке М 1 (пунктирная часть улитки Паскаля соответствует таким точкам М 2 , что векторы ХМ 1 и АХ противоположно направлены). Тогда OM 1 A = /3
2.4.6. Решение Паппа Александрийского при помощи конхоиды Никомеда
Конхоида Никомеда ― конхоида прямой, плоская алгебраическая кривая 4-го порядка (т.е. задаётся уравнением четвертой степени). Конхоида имеет две ветви, сама прямая конхоиды является асимптотой обеих ветвей.
Пусть острый угол АОВ требуется разделить на три равные части, причем эту трисекцию надо произвести при помощи конхоиды Никомеда. Зная принцип построения конхоиды Никомеда (Приложение №2), поступим так, как указывал Папп Александрийский. На одной из сторон данного угла, например на стороне О B , возьмем произвольную точку С и из нее на прямую ОА опустим перпендикуляр С D (рис.7). Теперь построим одну ветвь (правую) конхоиды Никомеда, приняв точку О за полюс, прямую С D за базис, а отрезок, равный 2 O С, за параметр. Эта конхоида пересечет стороны данного угла в точках Е и F . Через точку С проведем прямую, параллельную D Е, которая пересечет конхоиду в некоторой точке K . Соединим точку K с точкой О. Полученный угол АОК и будет составлять одну треть данного. Докажем это. Прежде всего обозначим точку пересечения прямых OK и С D через L . Середину отрезка L К обозначим через М и соединим ее прямой с точкой С. Нужные нам углы, как показано на чертеже, обозначим цифрами 1, 2, 3, 4, 5. Остается доказать, что угол 2 в два раза больше угла 1. Действительно, принимая во внимание свойство конхоиды, будем иметь:
L К = D Е = 2 O С.
L К = 2 LM и СМ = М K .
4 = 5 ( свойство равнобедренного треугольника),
5 = 1 ( свойство параллельных прямых),
2 = 3 ( свойство равнобедренного треугольника).
Далее, 3 = 4 + 5=2 5 ( свойство внешнего угла треугольника), или 2 = 2 1,
т. е. угол АОК составляет одну треть угла АОВ, что и требовалось доказать.
2.4.7. Решение Декарта
В связи с постепенным формированием алгебры математики проявляли все больший интерес к уравнениям, особенно к кубическим. В XI в. ими было получено уравнение трисекции угла (т. е. соотношение между sin 3а и sin а) и тем самым было показано, что задача трисекции угла сводится к решению кубического уравнения.
Пусть точки Q и Т делят дугу NР окружности с центром О на три равные части, радиусы О Q и ОТ пересекают хорду NР в точках R и U , а прямая, проходящая через точку Q параллельно прямой ТО, пересекает эту хорду в точке S (рис.8).
Так как Q N R = ( Q Т+ ТР)/2 = NQ = NOQ , то треугольники N OQ , QNR . и RQS являются подобными равнобедренными треугольниками. Поэтому N O : N Q = N Q : QR = QR : RS . Если N O =1 и N Q = z , то QR = z 2 и RS = z 3 . Ясно также, что NP + SR = NR +( SR + RU ) + UP = NQ + QT + TP = 3 NQ , т.е. NP = 3 z – z 3 .
2.4 .8. Решение с помощью конических сечений. Метод Шаля
Пусть требуется разделить угол AOB на три равные части.

Описываем вокруг О (Рис.10) произвольным радиусом окружность К и в А проводим к ней касательную t .Затем при О строим на ОВ произвольный угол ω и при А на t - тот же угол ω , но в
Получаемая таким путем точка пересечения Р при изменении ω описывает некоторую кривую h - гиперболу Шаля. Если X есть одна из точек пересечения гиперболы h с окружностью K , то
Именно, если Р 1 и Р 2 суть точки окружности К, отвечающие точке Р, то всегда
АОР 2 =2 ВОР 1 . Если теперь точки Р 1 и Р 2 совпадают в одной точке X , то AOX = 2 BOX .
2.4. 9 . Решение с помощью параллельных прямых
Кубические уравнения и сложные прямые, типа спиралей и конхоид, - это хорошо, но вот еще один метод трисекции угла, которым может овладеть любой ученик. Жаль, но этот метод подходит только для острых углов.
Для такого решения задачи необходимо по линейке с параллельными рёбрами внутри угла провести ряд линий, параллельных его обеим сторонам. Точки взаимного пересечения таких линий сразу разделят угол на любое искомое число равных частей.
Также можно провести трисекцию угла с помощью номографии (Приложение №3).
2.5. Свойство трисектрисы
Теорема Морлея: точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника.
Кардиоиды – это плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности такого же радиуса.
Но это не всё. Трисектрисы обладают еще некоторыми интересными свойствами, доказательство которых не сложно. Я приведу их в качестве задач ( Приложение №4 ).

Несмотря на то что, построения трисекции угла при помощи линейки и циркуля является древнейшей задачей геометрии, еще она не потеряла своей актуальности для энтузиастов науки.
Если представить, что вместо пучка параллельных прямых, будут концентрические дуги или окружности с бесконечно большими радиусами, то вышеприведенное свойство можно применить и к углу или окружности.
Действительно так. Длина дуги и окружности прямо пропорционально их радиусу. То есть, если их радиус увеличить или уменьшить на одну единицу отрезка, то и длина дуги или окружности так же увеличиться или уменьшится на одну единицу, равную длине первой прямой или дуги от вершин угла, рис.1. Из рисунка видно, что длина первой прямой или дуги от вершин угла, делить второй прямой или дуги на две равные части, третей прямой или дуги на три равные части и и. т.

Наши исследования показали, что используя эти свойства можно с высокой точности построить трисекцию угла. Например, дан некоторый угол α, рис. 2. Из свойства Темура следует, длина первой дуги радиусом R, разделит дугу окружности радиусом 3R на равные три части

Пусть дан некоторий угол α. На основани выше преведенного свойства угла разработали следующий способ построения трисекции угла:
1. При помощи циркуля проводим дугу радиусом R1=10 мм и R3=30 мм опирающие к сторонам m и n угла α, рис.2;
2. На основании свойства Темура длина первой дуги делит вторую на равные три части. Обычно в практике, в место длины дуги пользуются длиной хорды уперающей концам дуги, которая всегда меньше чем длина дуги. И именно по этому, построения трисекции угла остаётся абсалютно точно не решенной задачей геометрии.
И по этому в нашем случае, когда хорды АВ первой дуги откладываются три раза по дуге второй, то всегда остаётся остаток дуги СD. Если СОD представить как некоторий малый угол, то хорда ЕВ приближонно делит СD на три равные части.
3. От первой точки дуги радиусом 30 мм откладывая отрезок ЕВ, находим точку для проведения первой трисекции угла. От второй точки откладывая две отрезки ЕВ, имеем вторую точку трисекции угла. После этого проводится трисекции угла α.
Наше построение трисекции заданного угла показали, что хорды (по дуге R3=30 мм) упирающие к трисекциям практически равны. То есть разработанные нами способ и методика обеспечывают преимущественно высокой точности проведения трисекции угла.
Компьютерный анализ этого способа полностью поттвердил правильность нашего вывода, рис.3.

Для этого за практической точностью 1/3 угла α, мывзяли компьютерное построение трисекции данного угла равной 18,9826 0 . Из 3- рисунка видно, что первый и второй углы равны, а третий угол отличаются на величину +0,0001°.
Таким образом, теоретически обоснованный и практически реализо-ванный новый способ обеспечивает высокую точность и простату графических построений проведения трисекции угла. Т. е. практически можно считать точным.
Если заданный угол значительно больше, то остаток дуги СD также больше. В таких случаях рекомендуется раствор циркуля взять чут больше хорды АВ первой дуги.
Если дуга ЕВ значительно меньше, то проводя дугу радиусом 9R = 90 мм, получим дугу три раза длиннее СD. Откладывая хорды дуги СD на вновь построенной дуге, получим точку К. Праводим прямую ОК, которая и делить дугу СD на 1/3. Аналогически выполняя третье действие выше изложонного способа построим трисекцию данного угла, рис.4. Результаты которого оказались одинаковыми как на рис. 3.

Этим способом и методом можно делить заданный угол, на любое равное n ное число. По этому новый способ можно называть универсальным. Если n =7 или n =9, то радиусом второй дуги берётся 70 или 90 мм.
1. Атаджанов Р. К. Элементы конструктивной геометрии. Тошкент: Ўқитувчи, 1974 –С. 14–19.
Основные термины (генерируются автоматически): дуга, трисекция угла, вершина угла, длина дуги, заданный угол, угол, высокая точность, остаток дуги, отрезок ЕВ, построение трисекции угла.
Задача о трисекции угла состоит в том, чтобы разделить данный угол на три равные части.
Вместе с ещё двумя классическими задачами на построение — удвоением куба и квадратурой круга — задача о трисекции угла пришла из Древней Греции и на протяжении многих столетий занимала умы людей. Неоднократно пытались решить эти три задачи с помощью освящённых евклидовой геометрией инструментов — циркуля и линейки. Между тем, уже в древности математики догадались, что при использовании только циркуля и линейки эти задачи неразрешимы, а позднее это было и доказано. Попытки расширить инструментарий оказали большое влияние на древнегреческую математику, привели и к первым исследованиям конических сечений, и к исследованию сложных кривых, и к построению интересных инструментов.
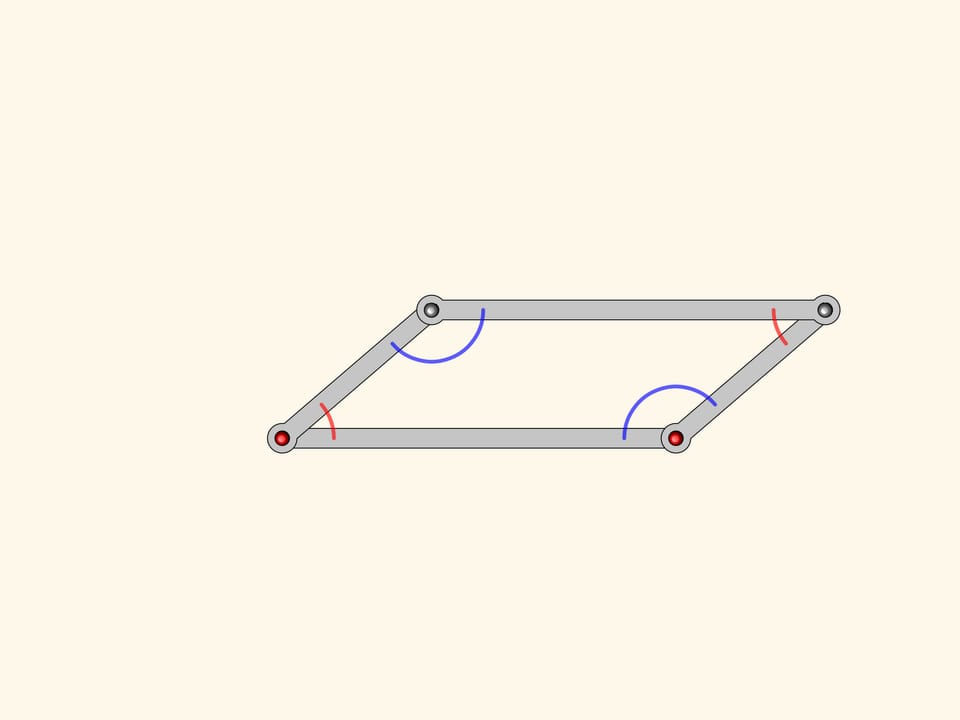
Рассмотрим шарнирный механизм, являющийся параллелограммом с двумя закреплёнными шарнирами. Из курса школьной математики вы помните, что противоположные углы параллелограмма равны. Это верно для любого параллелограмма, а значит, и для любого изгибания нашего механизма.
А для любого ли изгибания?
Альфред Брей Кемпе 1849—1922
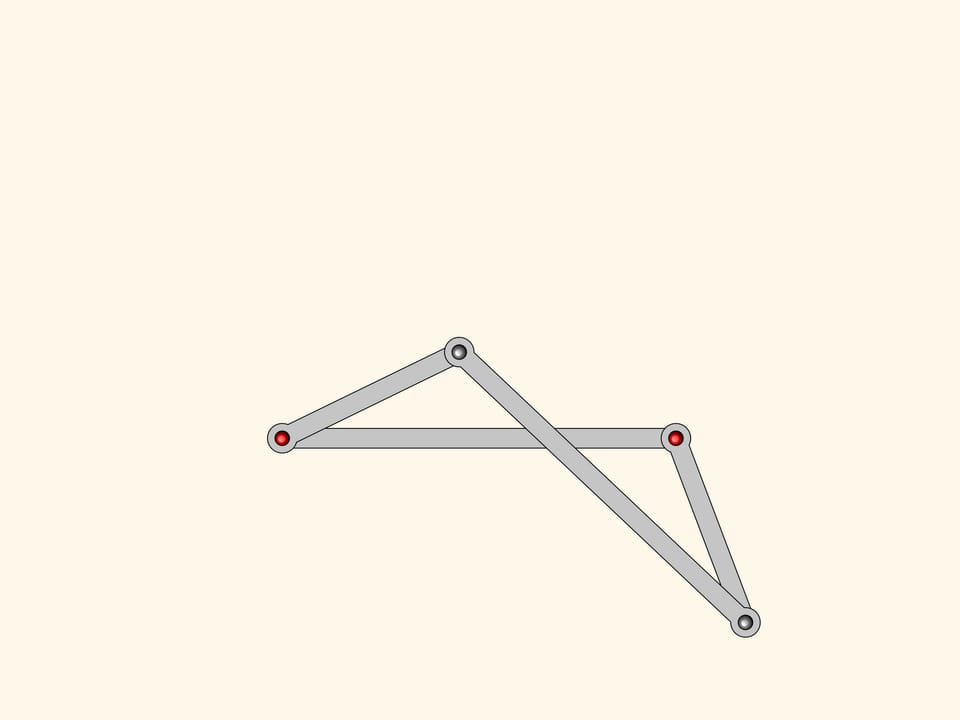
От параллелограмма антипараллелограмм унаследовал то, что две противоположные стороны равны между собой, и две накрест лежащие стороны также равны между собой. Оказывается, у нашей фигуры есть и соотношение на углы — у антипараллелограмма они попарно равны!
Прибавим к нашему антипараллелограмму более маленький, но подобный первому. У них есть один общий угол, а значит, углы при красном шарнире тоже равны.
Читайте также:

