Сообщение на тему многогранники и правильные многогранники

Обновлено: 02.07.2024

Все рёбра правильного многогранника равны, а также равны все двугранные углы, содержащие две грани с общим ребром.

Не существует правильного многогранника, гранями которого являются правильные многоугольники, если число их сторон \(6\) или больше, то есть правильные \(n\)-угольники, если n ≥ 6 .

Следовательно, не существует правильного многогранника, гранями которого являлись бы правильные \(n\)- угольники , если n ≥ 6 .

Только правильные треугольники, четырёхугольники (квадраты) и пятиугольники могут быть гранями правильного многогранника.

Существуют ли правильные многогранники с такими гранями, и сколько граней они имеют? Очевидно, меньшее возможное число граней — четыре.

1. Пусть количество рёбер правильного многогранника, выходящих из одной вершины, равно \(m\), а гранями являются правильные \(n\)-угольники.

\(Р\) (рёбра), \(m\), \(n\), где \(n\) и \(m\) — целые числа, и \(m ≥ 3\), \(n =\) \(3\), \(4\) или \(5\).

3. Так как каждое ребро соединяет две вершины, и в каждой вершине сходятся \(m\) рёбер, то \(2Р=Вm\).

7. Решим это уравнение при полученном в предыдущем доказательстве значении \(n =\) \(3\) и найдём допустимые значения \(m\).

Таким образом, теорема Эйлера разрешает существование следующих правильных многогранников:
1. \(m=3, n=3, P=6, Г=4\) — тетраэдр;
2. \(m=3, n=4, P=12, Г=6\) — куб;

3. \(m=3, n=5, P=30, Г=12\) — додекаэдр;
4. \(m=4, n=3, P=12, Г=8\) — октаэдр;
5. \(m=5, n=3, P=30, Г=20\) — икосаэдр.

Геометрия — сложная наука, включающая в себя множество категорий. Одна из них — стереометрия. Она ориентирована на изучение различных фигур в пространстве, включая многогранники. Они представляют собой замкнутые тела, составленные из нескольких многоугольников, называемых гранями. Каждая из них лежит в отдельной плоскости, в совокупности образуя объемную форму.

Основные понятия
Параметры фигуры
Правильные многогранники
Призма и ее особенности
Характеристики параллелепипеда
Пирамида и ее величины

Основные понятия

Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:

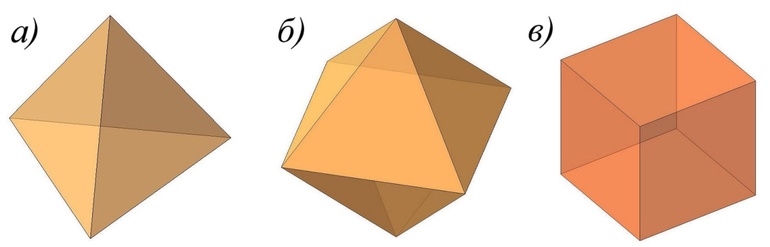
Выпуклые. Располагаются над плоскостью, которую можно провести через любой многоугольник, являющийся частью геометрического тела. В них все диагонали лежат внутри. Также тут все плоские углы в сумме дают 360 градусов.
Невыпуклые. Полностью или частично располагается над и под плоскостью, проведенной через выбранный многоугольник. Здесь некоторые диагонали могут располагаться снаружи.

Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.

Параметры фигуры

Независимо от вида, классификации и типа , каждый многогранник имеет определенные параметры. Все они являются одинаковыми для разных фигур. К ним относятся:

Грани. Это многоугольники, которые формируют основную фигуру;
Ребра . Это стороны плоских геометрических тел, каждая из которых является смежной между двумя многоугольниками. В противном случае многогранник не существует, т. к. не имеет замкнутую форму;
Вершины. Характеристика определяется числом граней. Чем их больше, тем, соответственно, больше вершин;
Диагонали. Секущие линии, конечными точками которых являются 2 вершины, каждая из них относится к разным граням;
Высоты. Это перпендикуляры, проведенные от одного основания к другому (в случае с призмой — от основания к вершине).

В случае с многогранниками часто используется такое понятие, как развертка . Ее обозначение включает в себя совокупность многоугольников, а также указание сторон и вершин. Чаще всего применяется в случае, когда необходимо составить модель из бумаги или иного подручного материала. Каждый элемент может быть отдельным, равно как следовать один за другим.

Для многогранников применяется теорема Эйлера. В ней участвует количество вершин (V), ребер ® и граней (G). Формула следующая : V — R + G = 2. Указанное равенство не рассматривается ни с какими другими геометрическими телами , даже если они лежат в трехмерном евклидовом пространстве.

Правильные многогранники

Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.

Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).

Призма и ее особенности

Призма — один из видов многогранников, включающий в себя многоугольники, расположенные в разных плоскостях. Но соединить их можно посредством параллельного переноса. У фигуры имеется основание и боковые ребра . Характерные особенности геометрического тела:

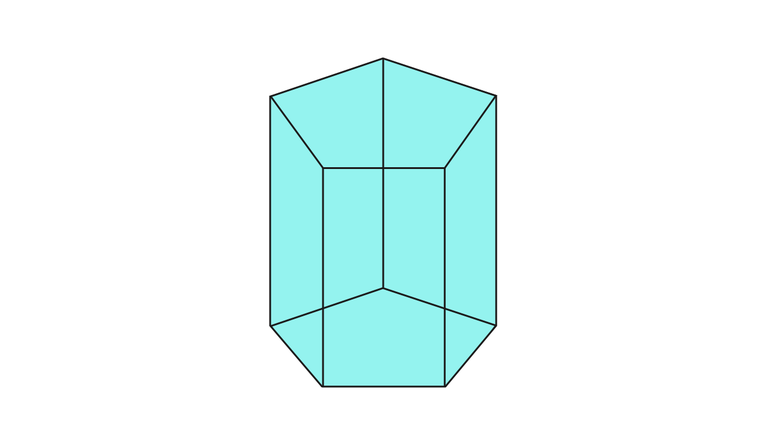
Основания полностью идентичны друг другу, несмотря на то, что лежат в разных плоскостях;
Основания параллельны друг другу;
Боковые ребра равны и параллельны;
Поверхность фигуры определяется суммой оснований и боковых граней (которых может быть неограниченное количество);
Высота призмы определяется проведением перпендикулярной прямой из любого основания к другому;
Площадь поверхности: S=Sбоковая + 2Sоснований;
Объем призмы: V=S*h, где S — площадь основания, а h — высоты фигуры;
Если основанием призмы является N -угольник, фигура считается N -угольной.

Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.

Характеристики параллелепипеда

Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:

Все грани, расположенные напротив , являются равными и параллельными;
Если отсутствуют общие вершины, они называются противолежащими;
Диагональ соединяет 2 вершины фигуры, расположенные в разных гранях;
Все диагонали параллелепипеда имеют одно пересечение, точка которого делит их на 2 равные части;
Пересечение диагоналей представляет собой центр симметрии.

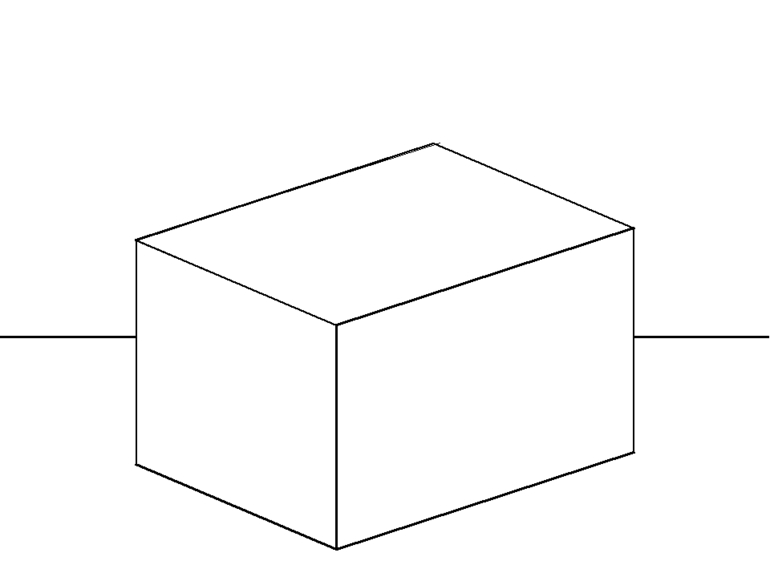
Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

Боковая поверхность равна сумме площадей граней;
Высота — перпендикуляр от основания к вершине;
Когда N — количество углов основания, пирамида называется N -угольной;
Формула объема многогранника: V = 1/3·S·h;
Формула площади всей поверхности: Sп = Sбоковых граней + Sоснования;
Все сечения, включая диагональные, являются треугольниками.

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Существует также такое понятие, как усеченная пирамида. Она получается только из правильной фигуры, если провести плоскость на противоположную от основания сторону, и убрать верхнюю часть. У данного тела отсутствует вершина, поскольку фактически она является квадратом , а не единичной точкой. Это не единственное отличие. К примеру, формулы, справедливые для классического формата, в данном случае неприемлемы.

Удивительный мир многогранников

Автор работы награжден дипломом победителя III степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Мое знакомство с многогранниками началось в пятом классе. На уроках мы учились строить изображения многогранников, определять количество вершин, граней и ребер, устанавливать соответствие между многогранником и его разверткой.

Цель исследования: познакомиться с видами многогранников, их применением в окружающем мире.

Объект исследования: многогранники.

Предмет исследования: многогранники и многогранные поверхности в окружающем мире.

- изучить исторический материал по данной теме;

- ознакомится с различными видами многогранников;

- рассмотреть область применения многогранников;

- изготовить модели многогранников.

Методы исследования: сбор информации, обработка данных, исследование, сравнение, анализ.

Виды многогранников

В течение многих веков математики проявляли живейший интерес к многогранникам. Интерес к ним обусловлен не только их красотой и оригинальностью, но и большой практической ценностью. Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне.

Многогранником называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Многоугольники, из которых составлен многогранник, называются его гранями. Стороны граней – рёбра многогранника, а концы рёбер – вершины многогранника.

Бывают выпуклыми и невыпуклыми. Выпуклый многогранник расположен по одну сторону от плоскости каждой своей грани. Невыпуклый многогранник расположен по разные стороны от плоскости одной из его граней.

Составлен из четырёх равносторонних треугольников.

Каждая его вершина является вершиной трёх треугольников.

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников.

Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.

Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов.

Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.

Кроме полуправильных многогранников из правильных многогранников - можно получить так называемые правильные звездчатые многогранники. Это правильные невыпуклые многогранники, у которых грани пересекаются. Их всего четыре. Иоганн Кеплер (1571 – 1630 гг.) - немецкий математик, астроном, оптик, для которого правильные многогранники были любимым предметом изучения, впервые описал малый звездчатый

додекаэдр и большой звездчатый додекаэдр. А спустя 200 лет Луи Пуансо Пуансо (1777-1859) построил большой икосаэдр и большой додекаэдр.

Многогранники вокруг нас

Многогранники в искусстве

Исторически математика играла важную роль в изобразительном искусстве.

Леонардо да Винчи (1452 — 1519) увлекался теорией многогранников и часто изображал их на своих полотнах.

Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники - филателисты и изображения многогранников. Почтовая марка, посвященная Леонарду Эйлеру с изображением икосаэдра, выпущена в 1983 г., в ГДР, к 200- летию ученого.

Н а выпущенной в 1980 году в Венгрии марке, изображен математик и астроном Иоганн Кеплер и его модель Вселенной на базе правильных многогранников.

Многогранники в архитектуре

И стория развития многогранников архитектуре уходит глубоко в историю. Многогранники начали использовать в архитектуре давно, более 7 тыс. лет. Великая пирамида в Гизе - эта грандиозная Египетская пирамида является древнейшим из семи чудес древности.

У Китая свои особенности использования многогранников в архитектуре. В основе лежит обязательно многогранник, который и служит основой для здания.

Многогранники не только придают прочность и устойчивость архитектурным сооружениям, но и красоту, изящество. Многие здания настолько красивы и сложны по своей форме, что требуют большого количества времени, сил. Современные архитекторы приобрели навык применения изящества, состоящие из множества сложных элементов, требующих большой работы.

П амятник правильным многогранникам в Германии

Стеклянная пирамида Лувра в Париже

З дание национальной библиотеки

Многогранники в химии и биологии

П равильные многогранники определяют форму кристаллических решеток некоторых химических веществ.Кристаллы многих металлов так же имеют форму куба (алюминий, серебро, свинец и др.)

Интересно, что именно икосаэдр оказался в центре внимания биологов. Чтобы установить форму вируса, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр.

В ирус краснухи

Вирус ветряной оспы

Многогранники в природе

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе.

Построенные пчелами соты представляют собой правильные шестиугольные призмы.

С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок. Снежинки - это звездчатые многогранники.

Мир кристаллов - мир не менее красивый и разнообразный. С кристаллами человечество познакомилось в глубокой древности. Связано это, в первую очередь, с их часто реализующейся в природе способностью самоограняться, т. е. самопроизвольно принимать форму изумительных по совершенству полиэдров. Даже современный человек, впервые столкнувшись с природными кристаллами, чаще всего не верит, что эти многогранники не являются делом рук искусного мастера.

Кристалл алмаза Кристалл рубина

Кристалл можно вырастить в домашних условиях.

Растворить соль в теплой воде. (Можно использовать поваренную соль (тогда кристалл будет прозрачный), но более красивый кристалл получается при использовании медного купороса (тогда кристалл будет синим). Можно использовать и другие вещества (сахар и различные соли)).

Когда соль перестанет растворяться в вашем растворе (получится перенасыщенный раствор), перелить его в другую емкость (лучше всего в прозрачную, так как тогда вы сможете легче наблюдать за ростом кристалла).

Постепенно наш кристалл будет расти и, когда он достигнет нужного размера, аккуратно вытащите его и обсушите.

Многогранники в географии

В географии – многогранники занимают важное место в исследовании залежей полезных ископаемых, которые тянутся вдоль икосаэдровододекаэдровой сетки.

Многогранники в жизни человека

С многогранниками мы знакомы с детских лет. О них напоминают окружающие нас предметы: кирпич, комната, книга, аквариум, различные упаковки и др.

В современном мире многие предметы интерьера имеют формы многогранников.

Многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений.

Многогранники и профессии

Плотник — профессия связана с механической обработкой дерева и превращением необработанной древесины в детали, конструкции и стройматериалы.

Слесарь — специалист по ручной (без использования станков) обработке металлов, включая операции по сборке и разборке на производстве или в быту.

Скульптор – это художник, занимающийся созданием скульптур, то есть произведений объемно-пространственной формы, трехмерных и осязаемых.

Модели многогранников

Практическим этапом моей работы стало изготовление моделей многогранников. Процесс изготовления моделей оказался очень увлекательным. Модели выполнены из разверток и в технике оригами.

Создание моделей правильных многогранников с помощью разверток

Чаще всего при создании моделей многогранников из плоских разверток используют такие развертки, в которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер. Например, при создании моделей правильных многогранников чаще всего используют следующие развертки.

Создание моделей многогранников методами оригами

Сегодня оригами переживает очередную волну интереса. Появились новые направления оригами и области его применения. Так, математики открыли множество возможностей для решения геометрических и топологических задач. Архитекторы и строители увидели в оригамном конструировании возможности для создания многогранных структур из плоского листа. Из бумаги можно построить удивительные конструкции.

При написании исследовательской работы я изучила дополнительную литературу и расширила свои знания по данному вопросу: узнала, что многогранники имеют красивые формы, они обладают богатой историей, познакомилась с видами многогранников. Решая поставленную проблему, я убедилась, что многогранники – это не просто геометрические тела , они окружают нас в жизни, в природе, в искусстве, архитектуре, науке. Многогранник – это величайшее открытие человечества. Систематизировав полученную информацию, я заметила, что в окружающем мире преобладают правильные многогранники.

Цель моей работы достигнута.

Список литературы и Интернет – ресурсов

Бунимович Е.А.Математика 6. – М.: Просвещение, 2016

Ворошилов А.В. Математика и искусство. - М.: Просвещение, 1992

Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для V – VI классов. – М: Мирос 1992.

Энциклопедия для детей. Я познаю мир. Математика. – М: Издательство АСТ, 1999

Многогранники не только занимают видное место в геометрии, но и встречаются в повседневной жизни каждого человека. Не говоря уже об искусственно созданных предметах обихода в виде различных многоугольников, начиная со спичечного коробка и заканчивая архитектурными элементами, в природе также встречаются кристаллы в форме куба (соль), призмы (хрусталь), пирамиды (шеелит), октаэдра (алмаз) и т. д.

Понятие многогранника, виды многогранников в геометрии

Геометрия как наука содержит раздел стереометрию, изучающую характеристики и свойства объёмных фигуры. Геометрические тела, стороны которых в трёхмерном пространстве образованы ограниченными плоскостями (гранями), носят название "многогранники". Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Тем не менее у всех многогранников есть общие свойства:

Все они имеют 3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.

Многогранники можно условно разделить на:

Виды выпуклых многогранников, состоящих из следующих классов: обычные или классические (призма, пирамида, параллелепипед), правильные (также называемые Платоновыми телами), полуправильные (второе название – Архимедовы тела).
Невыпуклые многогранники (звёздчатые).

Призма и её свойства

Стереометрия как раздел геометрии изучает свойства трёхмерных фигур, виды многогранников (призма в их числе). Призмой называют геометрическое тело, которое имеет обязательно две совершенно одинаковые грани (их также называют основаниями), лежащие в параллельных плоскостях, и n-ое число боковых граней в виде параллелограммов. В свою очередь, призма имеет также несколько разновидностей, в числе которых такие виды многогранников, как:

Параллелепипед - образуется, если в основании лежит параллелограмм - многоугольник с 2 парами равных противоположных углов и двумя парами конгруэнтных противоположных сторон. имеет перпендикулярные к основанию рёбра. характеризуется наличием непрямых углов (отличных от 90) между гранями и основанием.
Правильная призма характеризуется основаниями в виде правильного многоугольника с равными боковыми гранями.

Основные свойства призмы:

Конгруэнтные основания.
Все рёбра призмы равны и параллельны по отношению друг к другу.
Все боковые грани имеют форму параллелограмма.

Пирамида

Пирамидой называют геометрическое тело, которое состоит из одного основания и из n-го числа треугольных граней, соединяющихся в одной точке – вершине. Следует отметить, что если боковые грани пирамиды представлены обязательно треугольниками, то в основании может быть как треугольный многоугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании. Например, если в основании пирамиды лежит треугольник – это треугольная пирамида, четырёхугольник – четырёхугольная, и т. д.

Пирамиды – это конусоподобные многогранники. Виды многогранников этой группы, кроме вышеперечисленных, включают также следующих представителей:

Прямоугольная пирамида образуется тогда, когда одно из боковых рёбер пересекается с основанием под прямым углом. В таком случае это ребро справедливо также назвать высотой пирамиды.

В случае если все боковые рёбра пирамиды конгруэнтны (одинаковой высоты), то все они пересекаются с основанием под одним углом, а вокруг основания можно прочертить окружность с центром, совпадающим с проекцией вершины пирамиды.
Если в основании пирамиды лежит правильный многоугольник, то все боковые рёбра конгруэнтны, а грани являются равнобедренными треугольниками.

Правильный многогранник: виды и свойства многогранников

В стереометрии особое место занимают геометрические тела с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:

Тетраэдр.
Гексаэдр.
Октаэдр.
Додекаэдр.
Икосаэдр.

Своим названием правильные многогранники обязаны древнегреческому философу Платону, описавшему эти геометрические тела в своих трудах и связавшему их с природными стихиями: земли, воды, огня, воздуха. Пятой фигуре присуждали сходство со строением Вселенной. По его мнению, атомы природных стихий по форме напоминают виды правильных многогранников. Благодаря своему самому захватывающему свойству – симметричности, эти геометрические тела представляли большой интерес не только для древних математиков и философов, но и для архитекторов, художников и скульпторов всех времён. Наличие всего лишь 5 видов многогранников с абсолютной симметрией считалось фундаментальной находкой, им даже присуждали связь с божественным началом.

Гексаэдр и его свойства

В форме шестигранника преемники Платона предполагали сходство со строением атомов земли. Конечно же, в настоящее время эта гипотеза полностью опровергнута, что, однако, не мешает фигурам и в современности привлекать умы известных деятелей своей эстетичностью.

В геометрии гексаэдр, он же куб, считается частным случаем параллелепипеда, который, в свою очередь, является разновидностью призмы. Соответственно и свойства куба связаны со свойствами призмы с той лишь разницей, что все грани и углы куба равны между собой. Из этого вытекают следующие свойства:

Все рёбра куба конгруэнтны и лежат в параллельных плоскостях по отношению друг к другу.
Все грани – конгруэнтные квадраты (всего в кубе их 6), любой из которых может быть принят за основание.
Все межгранные углы равны 90.
Из каждой вершины исходит равное количество рёбер, а именно 3.
Куб имеет 9 осей симметрии, которые все пересекаются в точке пересечения диагоналей гексаэдра, именуемой центром симметрии.

Тетраэдр

Тетраэдр – это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.

Свойства правильного тетраэдра:

Все грани тетраэда – это равносторонние треугольники, из чего следует, что все грани четырёхгранника конгруэнтны.
Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.

Октаэдр и его свойства

Описывая виды правильных многогранников, нельзя не отметить такой объект, как октаэдр, который визуально можно представить в виде двух склеенных основаниями четырёхугольных правильных пирамид.

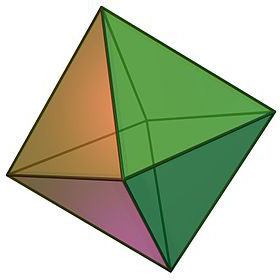
Само название геометрического тела подсказывает количество его граней. Восьмигранник состоит из 8 конгруэнтных равносторонних треугольников, в каждой из вершин которого сходится равное количество граней, а именно 4.
Так как все грани октаэдра равны, равны и его межгранные углы, каждый из которых равняется 60, а сумма плоских углов любой из вершин составляет, таким образом, 240.

Додекаэдр

Если представить, что все грани геометрического тела представляют собой правильный пятиугольник, то получится додекаэдр – фигура из 12 многоугольников.

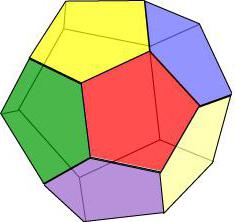
В каждой вершине пересекаются по три грани.
Все грани равны и имеют одинаковую длину рёбер, а также равную площадь.
У додекаэдра 15 осей и плоскостей симметрии, причём любая из них проходит через вершину грани и середину противоположного ей ребра.

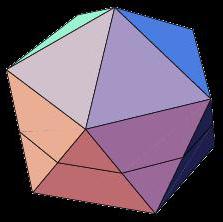
Икосаэдр

Не менее интересная, чем додекаэдр, фигура икосаэдр представляет собой объёмное геометрическое тело с 20 равными гранями. Среди свойств правильного двадцатигранника можно отметить следующие:

Все грани икосаэдра - равнобедренные треугольники.
В каждой вершине многогранника сходится пять граней, и сумма смежных углов вершины составляет 300.
Икосаэдр имеет так же, как и додекаэдр, 15 осей и плоскостей симметрии, проходящих через середины противоположных граней.

Полуправильные многоугольники

Кроме Платоновых тел, в группу выпуклых многогранников входят также Архимедовы тела, которые представляют собой усечённые правильные многогранники. Виды многогранников данной группы обладают следующими свойствами:

Геометрические тела имеют попарно равные грани нескольких типов, например, усечённый тетраэдр имеет так же, как и правильный тетраэдр, 8 граней, но в случае Архимедова тела 4 грани будут треугольной формы и 4 - шестиугольной.
Все углы одной вершины конгруэнтны.

Звёздчатые многогранники

Представители необъёмных видов геометрических тел – звёздчатые многогранники, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.

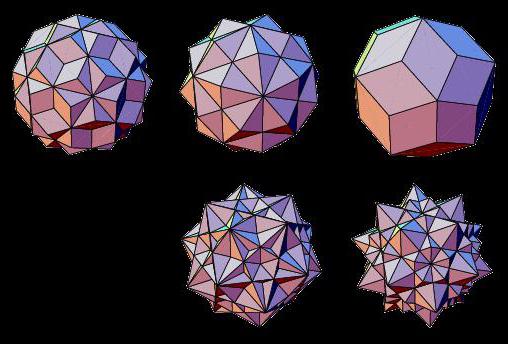
Таким образом, известны такие звёздчатые многогранники, как: звёздчатые формы октаэдра, додекаэдра, икосаэдра, кубооктаэдра, икосододекаэдра.

На протяжении многих столетий человечество пополняло свои знания в разнообразных областях наук. Стереометрия – наука о пространственных фигурах – неотъемлемо связана со многими дисциплинами, такими как математика, информатика и программирование, физика, биология, химия. В архитектуре также используются теоремы и следствия стереометрии.

Многогранники изучаются школьниками в 10-11 классах. Задания, связанные с правильными и полуправильными многогранниками, вызывают наибольшую трудность у ребят, особенно задачи на построение сечений. Знания об этих пространственных фигурах пригодятся на экзамене.

Многогранники имеют богатую историю, и всё же они включены в современный раздел математики. Теория многогранников имеет большое значение не только для теоретических исследований по геометрии, но и для областей прикладной математики – линейного программирования, теории оптимального управления и др. Наиболее необычными, интересными, гармоничными и красивейшими формами обладают правильные, полуправильные и звёздчатые многогранники.

Объект исследования – многогранники.

Работа состоит из введения, двух частей и заключения.

Список использованных источников включает 25 наименований.

Теоретическая часть 1. История многогранников

Знания о многогранниках применялись ещё с древнейших времён цивилизаций Египта, Месопотамии, Африки: например, были найдены ювелирные украшения в форме многогранников, а их возраст насчитывает несколько тысяч лет, а также игральные кости (археологами была найдена игральная кость в форме додекаэдра, датируемая 1000 годом до н. э.).

Пифагор Самосский (около 582 года до н. э. – 507 год до н. э.) создал космологическое учение, связавшее правильные многогранники с устройством Вселенной. Пифагорейцы считали, что элементы первооснов бытия имеют форму правильных многогранников, а именно: огонь – тетраэдр, земля – гексаэдр, воздух – октаэдр, вода – икосаэдр. Вся Вселенная, по мнению древних, имела форму додекаэдра [10].

Иоганн Кеплер в своей работе "Тайна мироздания" в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы [6].

В 1854 году Артур Кэли дал имена двум многогранникам Кеплера (что пытался описать звёздчатые многогранники): малый звёздчатый додекаэдр и большой звёздчатый додекаэдр. Луи Пуансо обнаружил ещё два новых: большой додекаэдр и большой икосаэдр. В 1812 году Огюстен Луи Коши смог доказать гипотезу Пуансо о том, что существуют только 4 единственно возможных правильных звёздчатых многогранника (4 многогранника Кеплера-Пуансо) [3].

2. Определения многогранника, многогранной поверхности, развёртки многогранника и его элементов (рёбер, граней, вершин, двугранных углов и диагоналей)

Существуют различные определения понятия многогранник, которые можно встретить в известных учебниках.

Ж. Адамар называет многогранником тело, ограниченное со всех сторон плоскостями [1].

Многогранник имеет рёбра, грани, вершины, двугранные углы и диагонали, определения которых можно увидеть в учебниках А. П. Киселева и А. Ю. Калинина [14, 13]:

Общие стороны смежных многоугольников называются рёбрами многогранника.

Многоугольники, которые ограничивают многогранник, называются его гранями.

Грани многогранника, сходящиеся в одной точке, образуют двугранный угол;

Вершины таких многогранных углов называются вершинами многогранника.

Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями этого многогранника.

Многогранной поверхностью называется поверхность, составленная из многоугольников. Процесс составления многогранной поверхности из многоугольников можно представить себе как операцию склеивания этой поверхности из многоугольников [15].

3. Теорема Эйлера

Теорему Эйлера историки математики называют первой теоремой топологии – раздела геометрии, который изучает свойства фигур, не меняющихся при непрерывных деформациях, допускающих любые растяжения и сжатия, но без разрывов или дополнительных склеек. Соотношение Эйлера

для выпуклых многогранников является как раз таким топологическим свойством [20]. Сформулируем и докажем данную теорему Эйлера:

Теорема 1. Для любого выпуклого многогранника сумма числа его вершин В и числа его граней Г без числа рёбер Р равна двум, т. е.

Доказательство [22]. Представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим сетку (рис. 1, а), содержащую Г' = Г – 1 многоугольников (которые по-прежнему будут называться гранями), В вершин и Р рёбер.

Если для этой сетки выполняется соотношение

То для исходного многогранника будет справедливо требуемое соотношение (*).

Покажем, что требуемое соотношение (**) не изменится, если в каком-нибудь многоугольнике сетки провести диагональ. Действительно, после проведения такой диагонали в сетке будет В вершин, Р + 1 рёбер и Г' + 1 граней, и, следовательно,

Пользуясь этим свойством, проведём в сетке диагонали, разбивающие входящие в неё многоугольники на треугольники (рис. 1, б), и для полученной сетки покажем выполнимость соотношения (**). Для этого будем последовательно убирать внешние рёбра сетки, уменьшая в ней количество треугольников.

При этом возможны два случая:

а) для удаления треугольника АВС требуется снять два ребра, в нашем случае АВ и ВС;

б) для удаления треугольника MKN требуется снять одно ребро, в нашем случае MN.

В обоих случаях соотношение (**) не изменится. Например, в первом случае после удаления треугольника сетка будет состоять из В – 1 вершин,

Таким образом, удаление одного треугольника не меняет соотношение (**). Продолжая этот процесс удаления треугольников, в конце концов мы придём к сетке, состоящей из одного треугольника. Для такой сетки В = 3,

Р = 3, Г' = 1, и, следовательно, В – Р + Г' = 1. Значит соотношение (**) имеет место и для исходной сетки, откуда окончательно получаем, что для данного многогранника справедливо соотношение (*).

4. Правильные многогранники 4.1. Теорема о существовании пяти правильных многогранников

Многогранник называется выпуклым, если он лежит с одной стороны от плоскости любой своей грани, т. е. плоскость его любой грани является его опорной плоскостью [2].

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и, кроме того, в каждой его вершине сходится одно и то же число рёбер [5].

Многогранник называется правильным, если [19]:

1) все его грани равны и правильны;

2) все его многогранные углы равны и правильны.

Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще

n-угольники при . Каждая вершина правильного многоугольника может быть вершиной любо трёх, четырёх или пяти равносторонних треугольников, либо трёх квадратов, либо трёх правильных пятиугольников

Доказательство [5]. В самом деле, угол правильного n-угольника при n не меньше 120. С другой стороны, при каждой вершине многогранника должно быть не менее трёх плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные

n-угольники при n, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 120. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше .

Рассмотрим важную теорему о существовании ровно пяти правильных многогранников:

Теорема 2. Существует только пять видов правильных многогранников.

При этом мы относим к одному виду те многогранники, у которых многогранные углы имеют одно и то же число рёбер, а грани – одно и то же число сторон.

Доказательство [1]. Пусть m – число сторон каждой грани правильного многогранника; n – число рёбер каждого многогранного угла.

Если принять прямой угол за единицу, то каждый угол какой-либо грани выразится числом ; но сумма n плоских углов, примыкающих к одной вершине, должна быть меньше четырёх прямых; следовательно, каждый из них должен быть меньше .

Причём равенство исключено.

Это неравенство и даёт искомое решение. Действительно, каждое из чисел m и n больше или равно 3, но оба они не могут быть больше 3; так как для и , имеем .

Следовательно, по крайней мере одно из чисел m и n равно 3. Допустим, что это будетm: в равенстве (1) можно переставить числа m и n, так как оно симметрично относительно этих двух чисел.

При этом будем иметь:

Следовательно, n может иметь только значения 3, 4 и 5.

Симметрия неравенства (1) относительно чисел mи n не должна нас удивлять; в самом деле, каждое из этих чисел становится на место другого, если от некоторого многогранника перейти к многограннику, ему сопряжённому. Каждый раз, как m и n будут различны, мы будем иметь пару сопряжённых решений – всего-навсего получим следующие пять решений:

В соответствие с теоремой получаем следующие правильные многогранники (Платоновы тела): тетраэдр, куб, октаэдр, додекаэдр, икосаэдр (табл. 1).

Читайте также: