Сообщение на тему метод эйлера
Обновлено: 05.07.2024
Решение дифференциального уравнения численным методом. Исправленный и модифицированный метод Эйлера. Значение метода Эйлера. Описание алгоритма главной программы. Сравнение результатов полученных при использовании программы, а также ручным способом.
| Рубрика | Математика |
| Вид | контрольная работа |
| Язык | русский |
| Дата добавления | 20.07.2012 |
| Размер файла | 310,5 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Уравнения, содержащие производную функции одной переменной, возникают во многих областях прикладной математики. Вообще говоря, любая физическая ситуация, где рассматривается степень изменения одной переменной по отношению к другой переменной, описывается дифференциальным уравнением, а такие ситуации встречаются довольно часто.
Решение обыкновенных дифференциальных уравнений (нелинейных) первого порядка с начальными данными (задача Коши) - классическая область применения численных методов. Имеется много разностных методов, часть из которых возникла в домашинную эпоху и оказалось пригодным для современных ЭВМ.
В этой программе использовался метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Этот метод имеет довольно большую ошибку; кроме того, он очень часто оказывается неустойчивым - малая начальная ошибка быстро увеличивается с ростом Х. Поэтому чаще используют более точные методы, такие как: исправленный метод Эйлера и модифицированный метод Эйлера. Нужно, однако, заметить, что метод Эйлера является методом Рунге - Кутта первого порядка.
Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений - это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически-симметричных полях и многое другое).
1. Постановка задачи
1.1 Метод Эйлера
Решить дифференциальное уравнение у / =f (x, y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi) (i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относится к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Рассмотрим дифференциальное уравнение первого порядка
с начальным условием
Требуется найти решение уравнения (1) на отрезке [а, b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
При этом искомая интегральная кривая у=у(х), проходящая через точку М0(х0, у0), заменяется ломаной М0М1М2… с вершинами Мi(xi, yi) (i=0,1,2,…); каждое звено МiMi+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку Мi, смотри рисунок 1.
Если правая часть уравнения (1) в некотором прямоугольнике R <|x-x0|a, |y-y0|b> удовлетворяет условиям:
|df/dx|=|df/dx+f (df/dy)| M (M=const), то имеет место следующая оценка погрешности:
где у(хn) - значение точного решения уравнения(1) при х=хn, а уn - приближенное значение, полученное на n-ом шаге.
Формула (3) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения уn * оценивается формулой
Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.
1.2 Исправленный метод Эйлера
В исправленном методе Эйлера мы находим средний тангенс наклона касательной для двух точек: xm, ym и xm+h, ym+hy'm. Последняя точка есть та самая, которая в простом методе обозначалась xm+1, ym+1. Геометрический процесс нахождения точки xm+1, ym+1 можно проследить по рисунку 2. С помощью метода Эйлера находится точка xm+h, ym+hy'm, лежащая на прямой L1. В этой точке снова вычисляется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая L2. Усреднение двух тангенсов дает прямую L'3. Наконец, через точку xm, ym мы проводим прямую L3 параллельную L'3. Точка, в которой прямая L3 пересечется с ординатой, восстановленной из x= xm+1=xm+h, и будет искомой точкой y= ym+1= ym+hy'm. Тангенс угла наклона L3 равен:
Уравнение линии L3 при этом записывается в виде:
Соотношения 5, 6, 7 и 8 описывают исправленный метод Эйлера. (рис. 2)
1.3 Модифицированный метод Эйлера
Этот метод более точен. Рассмотрим дифференциальное уравнение (1) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участке [x0, x0+h] интегральную кривую заменим прямой линией. Получаем точку Мк(хк, ук).
Получаем точку Nk / . В этой точке строим следующую касательную:
Из точки Мк проводим прямую с угловым коэффициентом бк и определяем точку пересечения этой прямой с прямой xк1. Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
Эти формулы называются рекуррентными формулами метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции yк+1/2 в точках xк+1/2, затем находят значение правой части уравнения (1) в средней точке y / k+1/2=f(xk+1/2, yk+1/2) и определяют yк+1.
Не обошла стороной вычислительная математика и дифференциальные уравнения! Сегодня на уроке мы познакомимся с основами приближённых вычислений в этом разделе математического анализа, после чего перед вами приветливо распахнутся толстые-претолстые книги по теме. Ибо вычислительная математика стороной диффуры ещё как не обошла =)
Перечисленные в заголовке методы предназначены для приближённого нахождения решений дифференциальных уравнений, систем ДУ, и краткая постановка наиболее распространённой задачи такова:
Рассмотрим дифференциальное уравнение первого порядка , для которого требуется найти частное решение, соответствующее начальному условию . Что это значит? Это значит, нам нужно найти функцию (предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку .
Идея методов Эйлера и Рунге-Кутты состоит в том, чтобы заменить фрагмент графика ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)
Найти частное решение дифференциального уравнения , соответствующее начальному условию , методом Эйлера на отрезке с шагом . Построить таблицу и график приближённого решения.
Разбираемся. Во-первых, перед нами обычное линейное уравнение, которое можно решить стандартными способами, и поэтому очень трудно устоять перед соблазном сразу же найти точное решение:
– желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию и является корнем уравнения .
Что нужно сделать? Нужно найти и построить ломаную, которая приближает график функции на промежутке . Поскольку длина этого промежутка равна единице, а шаг составляет , то наша ломаная будет состоять из 10 отрезков:
Представим дифференциальное уравнение в виде :
и так далее – до победного конца.
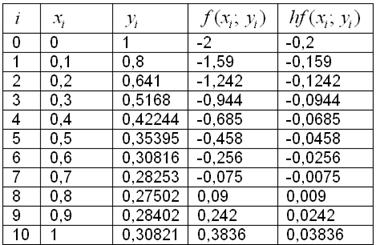
Результаты вычислений удобно заносить в таблицу:
А сами вычисления автоматизировать в Экселе – потому что в математике важен не только победный, но ещё и быстрый конец:)
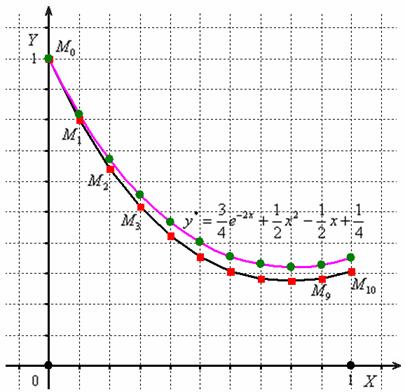
По результатам 2-го и 3-го столбцов изобразим на чертеже 11 точек и 10 отрезков, соединяющих смежные точки. Для сравнения я построю график точного частного решения :
Существенным недостатком простого метода Эйлера является слишком большая погрешность, при этом легко заметить, что погрешность имеет тенденцию накапливаться – чем дальше мы уходим от точки , тем преимущественно больше становится расхождение между приближением и истиной. Это объяснимо самим принципом, который Эйлер положил в основу своего метода: отрезки параллельны соответствующим касательным к графику функции в точках . Данный факт, кстати, тоже хорошо просматривается по чертежу.
Как можно улучшить приближение? Первая мысль – измельчить разбиение. Разделим отрезок , например, на 20 частей. Тогда шаг составит: , и совершенно понятно, что ломаная из 20 звеньев заметно точнее приблизит частное решение. С помощью того же Экселя не составит труда обработать 100-1000 и даже миллион (!) промежуточных отрезков, однако зададимся вопросом: а нельзя ли КАЧЕСТВЕННО улучшить метод?
Но перед тем как раскрыть этот вопрос, не могу не остановиться на неоднократно прозвучавшей сегодня фамилии. Читая биографию Леонарда Эйлера, просто поражаешься, как невероятно много может успеть сделать за свою жизнь человек! Сопоставимо вспомнился только К.Ф. Гаусс. …Вот и мы постараемся не потерять мотивацию к обучению и новым открытиям:))
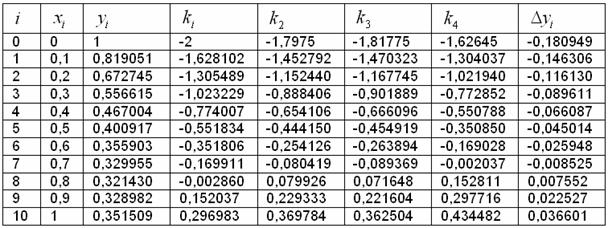
Усовершенствованный метод Эйлера
Рассмотрим тот же самый пример: дифференциальное уравнение , частное решение, удовлетворяющее условию , промежуток и его разбиение на 10 частей
( – длина каждой части).
Алгоритм решения работает в том же русле, но формула, как нетрудно догадаться, усложняется:
, где
Умножаем результат на шаг разбиения:
Алгоритм заходит на второй круг, не поленюсь, распишу его подробно:
Рассчитываем и находим её 2-й аргумент:
и его произведение на шаг:
Далее рассматриваем пару и т.д.
Однако нет пределов совершенству. Одна голова хорошо, а две – лучше. И снова немецкие:
Классический метод Рунге-Кутты 4-го порядка
Готовы? Ну тогда начинаем:))
Первая строка запрограммирована, и я копирую формулы по образцу:
Не думал, что так быстро разделаюсь с методом Рунге-Кутты =)
В чертеже нет смысла, поскольку он уже не показателен. Давайте лучше проведём аналитическое сравнение точности трёх методов, ибо когда известно точное решение , то грех не сравнить. Значения функции в узловых точках элементарно рассчитываются в том же Экселе – один раз забиваем формулу и тиражируем её на остальные .
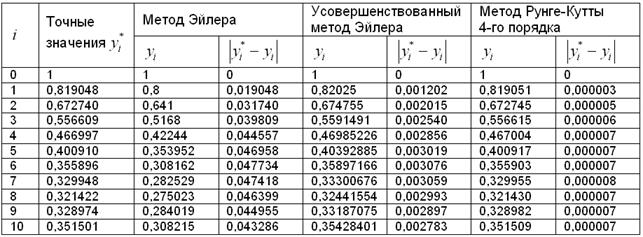
В нижеследующую таблицу я сведу значения (для каждого из трёх методов) и соответствующие абсолютные погрешности приближённых вычислений:
Как видите, метод Рунге-Кутты даёт уже 4-5 верных знака после запятой по сравнению с 2 верными знаками усовершенствованного метода Эйлера! И это не случайность:
– Усовершенствованный метод Эйлера гарантирует точность: (смотрим на 2 нуля после запятой в средней колонке погрешностей).
– И, наконец, классический метод Рунге-Кутты обеспечивает точность .
Изложенные оценки погрешностей строго обосновывается в теории.
Как можно ЕЩЁ улучшить точность приближения? Ответ прямо-таки философский: качеством и/или количеством =) В частности, существует и другие, более точные модификации метода Рунге-Кутты. Количественный путь, как уже отмечалось, состоит в уменьшении шага, т.е. в разбиении отрезка на бОльшее количество промежуточных отрезков. И с увеличением этого количества ломаная всё больше и больше будет походить на график точного решения и в пределе – совпадёт с ним.
Безусловным достоинством рассмотренных методов, является тот факт, что они применимы к уравнениям с очень сложной правой частью. И безусловный недостаток – далеко не каждый диффур можно представить в таком виде.
Но почти всё в этой жизни поправимо! – ведь мы рассмотрели лишь малую толику темы, и моя фраза о толстых-претолстых книгах была вовсе не шуткой. Существует великое множество приближённых методов нахождения решений ДУ и их систем, в которых применяются, в том числе, принципиально другие подходы. Так, например, частное решение можно приблизить степенным рядом. Однако это уже статья другого раздела.
Надеюсь, мне удалось разнообразить скучноватую вычислительную математику, и вам было интересно!
Спасибо за внимание!
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
В математике , то метод Эйлера , названный в честь математика Леонарда Эйлера (1707 - 1783), является численная процедура для решения первого порядка дифференциальных уравнений путем аппроксимации с начальным условием . Это простейший метод численного решения дифференциальных уравнений .
Резюме
Принцип метода

Иллюстрация явного метода Эйлера: продвижение осуществляется аппроксимацией по касательной в начальной точке.
Метод Эйлера - это элементарный численный метод решения дифференциальных уравнений первого порядка вида
∀ Икс ∈ я , ты ′ ( Икс ) знак равно ж ( Икс , ты ( Икс ) )
При заданном начальном условии метод обеспечивает для любой точки b ∈ I серию приближений значения u ( b ), которое принимает, когда оно существует, решение уравнения, которое соответствует этому начальному условию. Различные наборы условий на f могут гарантировать сходимость этой последовательности. ( в , ты ( в ) ) ∈ я × р > ( ты нет ( б ) ) нет ∈ НЕТ (б)) _ >>
Значение u n ( b ) получается путем вычисления n промежуточных значений приближенного решения в точках, регулярно распределенных между a и b , которые задаются формулой ( y я ) я ∈ < 0 , нет >) _ >> ( Икс я ) я ∈ < 0 , нет >) _ >>
Явный Эйлер
Распространяя это обозначение на x 0 = a , y 0 = u ( a ) и x n = b , y n = u n ( b ) и используя приближение производной
Мы выводим следующее соотношение:
Промежуточные значения тогда задаются рекуррентным соотношением
что является явной схемой Эйлера.
Неявный Эйлер
Обратите внимание, что мы также можем приблизиться к производной в точке x i +1 с помощью того же соотношения
мы выводим рекуррентное соотношение
что является неявной схемой Эйлера. Следует отметить, что на этой диаграмме член y i +1 появляется с обеих сторон уравнения, что ограничивает использование численных методов разрешения типа отношения Ньютона-Рафсона для определения y i +1 на каждой итерации, если функция f нелинейна.
Примеры
Приложение к интеграции
Интеграцию непрерывной функции на отрезке можно рассматривать как специальный случай , когда функция F непрерывна и зависит только от й : . Затем мы докажем, используя равномерную непрерывность f на [ a , b ] ( теорема Гейне ), что последовательность является Коши и, следовательно, сходится по полноте . ты ′ ( Икс ) знак равно ж ( Икс ) ( ты нет ( б ) ) нет ∈ НЕТ (б)) _ >> р >
Фактически у нас есть: y нет знак равно час ∑ k знак равно 0 нет ж ( k час ) знак равно 1 нет ∑ k знак равно 0 нет ж ( k ( б - в ) нет ) . = h \ sum _ ^ f (kh) = > \ sum _ ^ f \ left ( > \ right).>
Мы узнаем метод прямоугольников слева для вычисления точного решения . ∫ в Икс нет ж ( ты ) d ты > f (u) \, du>
Учитывая функцию и начальные значения x 0 = 1 и y 0 = F ( x 0 ) = 1 ⁄ 4 . ж : Икс ↦ Икс 2 >>
Вычисление значений F ( x 1 ), F ( x 2 ), F ( x 3 )… позволяет получить графическое представление F в виде отрезков [A 0 A 1 ], [A 1 A 2 ], [A 2 A 3 ]…
Функция f имеет первообразную с x 0 = 1 и y 0 = G ( x 0 ) = 1 ⁄ 4 . грамм : Икс ↦ Икс 2 4 > >>
Кривая (C), представляющая G , помещена здесь на том же графике для визуализации расчета касательных.
Аффинная функция кусочно является аппроксимацией исходной G .
Линейный случай
Еще один классический случай , когда е является линейной функцией у : . На диаграмме показано: ты ′ знак равно против ты
y нет + 1 знак равно y нет + час против y нет знак равно ( 1 + против час ) y нет , = y_ + hcy_ = (1 + ch) y_ ,> является
y нет знак равно ( 1 + против час ) нет знак равно ( 1 + против б - в НЕТ ) нет . = (1 + ch) ^ = \ left (1 + c > \ right) ^ .>
В конечной точке находится приблизительное значение точного решения при условии, что N достаточно велико: y НЕТ знак равно ( 1 + против б - в НЕТ ) НЕТ ≃ exp ( против ( б - в ) ) = \ left (1 + c > \ right) ^ \ simeq \ exp (c (ba))> .
Также можно отметить, что при слишком большом шаге последовательность (геометрическая) принимает все больше значений и расходится с решением (диаграмма нестабильна ). Обходной путь - использовать неявный метод Эйлера : y нет + 1 знак равно y нет + час против y нет + 1 ⟺ y нет знак равно ( 1 - против час ) - нет . = y_ + hcy_ \ Longleftrightarrow y_ = (1-ch) ^ .>
Эта диаграмма более устойчива численно и гарантирует более простую сходимость к решению.
Ошибка метода
Метод Эйлера прост, но наведенная ошибка может быть довольно высокой, если шаг выбран слишком большим. Действительно, вычисление ошибки согласованности дает формулу Тейлора-Лагранжа : ϵ нет знак равно ты ( т нет + 1 ) - ты нет + 1 знак равно ты ( т нет + 1 ) - ты ( т нет ) - час ж ( т нет , ты ( т нет ) ) знак равно ты ( т нет + 1 ) - ты ( т нет ) - час ты ′ ( т нет ) знак равно 1 2 час 2 ты ″ ( т нет ) + о ( час 2 ) . = u (t_ ) - u_ = u (t_ ) - u (t_ ) - hf (t_ , u (t_ )) = u (t_ ) - u (t_ ) - hu '(t_ ) = > h ^ u '' (t_ ) + o (h ^ ).>

Темой этой статьи как раз и будет реализация такого интегрирования.
Интегрирование уравнений движения
Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.
Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.
Ускорение — это темп изменения скорости от времени:
Аналогично, скорость — это темп изменения позиции от времени:
Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.
Численное интегрирование
Если вы не изучали дифференциальные уравнения в вузе, то можете вздохнуть спокойно — вы почти в такой же ситуации, что и те, кто их изучал, потому что мы не будем решать дифференциальные уравнения аналитически. Вместо этого мы будем искать решение численным интегрированием.
Вот как работает численное интегрирование: во-первых, начнём с исходной позиции и скорости, затем сделаем небольшой шаг вперёд, чтобы найти скорость и позицию в будущем. Затем повторим это, двигаясь вперёд небольшими шагами, используя результат предыдущих вычислений как исходную точку следующих.
Но как нам найти изменение скорости и позиции на каждом шаге?
Ответ лежит в уравнениях движения.
Теперь мы можем представить уравнения движения в понятном всем виде:
Интуитивно это понятно: если вы находитесь в автомобиле, движущемся со скоростью 60 км/ч, то за один час вы проедете 60 км. Аналогично, автомобиль, ускоряющийся на 10 км/ч в секунду, через 10 секунд будет двигаться на 100 км/ч быстрее.
Разумеется, эта логика сохраняется, только когда ускорение и скорость постоянны. Но даже если они меняются, то это для начала вполне неплохая аппроксимация.
Давайте представим это в коде. Начнём с стационарного объекта массой один килограмм и приложим к нему постоянную силу в 10 кН (килоньютонов) и сделаем шаг вперёд, принимая, что один временной шаг равен одной секунде:
Вот каким будет результат:
Как вы видите, на каждом шаге мы знаем и позицию, и скорость объекта. Это и есть численное интегрирование.
Явный метод Эйлера
Вид интегрирования, который мы только что использовали, называется явным методом Эйлера.
Он назван в честь швейцарского математика Леонарда Эйлера, впервые открывшего эту технику.
Интегрирование Эйлера — это простейшая техника численного интегрирования. Она точна на 100% только когда темп изменений в течение шага времени постоянен.
Поскольку в примере выше ускорение постоянно, интегрирование скорости выполняется без ошибок. Однако мы ещё интегрируем и скорость для получения позиции, а скорость увеличивается из-за ускорения. Это значит, что в проинтегрированной позиции возникает ошибка.
Но насколько велика эта ошибка? Давайте выясним!
Существует аналитическое решение движения объекта при постоянном ускорении. Мы можем использовать его, чтобы сравнить численно интегрированную позицию с точным результатом:
Через 10 секунд объект должен был переместиться на 500 метров, но явным метод Эйлера даёт нам результат 450. То есть погрешность в целых 50 метров всего за 10 секунд!
Кажется, что это невероятно плохо, но в играх обычно для шага физики берётся не такой большой временной интервал. На самом деле, физика обычно вычисляется с частотой, примерно равной частоте кадров дисплея.
Если задать шаг dt = 1 ⁄100, то мы получим гораздо лучший результат:
Как вы видите, это достаточно хороший результат, определённо вполне достаточный для игры.
Почему явный метод Эйлера не (всегда) так уж хорош
С достаточно малым шагом времени явный метод Эйлера при постоянном ускорении даёт вполне достойные результаты, но что будет, если ускорение не постоянно?
Хорошим примером переменного ускорения является система пружинного амортизатора.
В этой системе масса присоединена к пружине, и её движение гасится чем-то вроде трения. Существует сила, пропорциональная расстоянию до объекта, которая притягивает его к исходной точке, и сила, пропорциональная скорости объекта, но направленная в противоположном направлении, которая замедляет его.
Здесь ускорение в течение шага времени совершенно точно изменяется, но эта постоянно меняющаяся функция является сочетанием позиции и скорости, которые сами постоянно изменяются за шаг времени.
Вот пример гармонического осциллятора с затуханием. Это хорошо изученная задача, и для него существует аналитическое решение, которое можно использовать для проверки результата численного интегрирования.
Давайте начнём со слабозатухающей системы, в которой масса колеблется рядом с исходной точкой, постепенно замедляясь.
Вот входные параметры системы масса-пружина:
- Масса: 1 килограмм
- Исходная позиция: 1000 метров от исходной точки
- Коэффициент упругости по закону Гука: k = 15
- Коэффициент затухания по закону Гука: b = 0.1

Если для интегрирования этой системы мы применим явный метод Эйлера, то получим следующий результа, который я отмасштабировал по вертикали:

Вместо затухания и сближения с исходной точкой, система со временем набирает энергию!
При интегрировании явным методом Эйлера и с dt= 1 ⁄100 такая система нестабильна.
К сожалению, поскольку мы уже интегрируем с малым шагом времени, то не имеем практичных способов повышения точности. Даже если мы уменьшим шаг времени, то всегда будет коэффициент упругости k, при котором мы получим такое поведение.
Симплектический метод Эйлера
Мы можем рассмотреть ещё один интегратор — симплектический метод Эйлера.
В большинстве коммерческих игровых физических движков используется этот интегратор.
Переход от явного к симплектическому методу Эйлера заключается только в замене:
Использование симплектического интегратора Эйлера при dt = 1 ⁄100 для системы пружинного амортизатора даёт стабильный результат, очень близкий к точному решению:

Даже несмотря на то, что симплектический метод Эйлера имеет ту же степень точности, что и явный метод (степень 1), при интегрировании уравнений движения мы получаем намного лучший результат, потому что оно является симплектическим.
Существует множество других методов интегрирования
И теперь нечто совершенно другое.
Неявный метод Эйлера — это способ интегрирования, хорошо подходящий для интегрирования жёстких уравнений, которые при других методах становятся нестабильными. Его недостаток заключается в том, что он требует решения системы уравнений на каждом шаге времени.
Интегрирование Верле обеспечивает бо́льшую точность, чем неявный метод Эйлера, и требует меньше памяти при симуляции большого числа частиц. Это интегратор второй степени, который тоже является симплектическим.
Существует целое семейство интеграторов, называемое методами Рунге-Кутты. На самом деле, явный метод Эйлера считается частью этого семейства, но в него входят интеграторы и более высокого порядка, самым классическим из которых является метод Рунге-Кутты порядка 4 (Runge Kutta order 4) или просто RK4.
Это семейство интеграторов названо в честь открывших их немецких физиков: Карла Рунге и Мартина Кутты.
RK4 — это интегратор четвёртого порядка, то есть накапливаемая ошибка имеет порядок четвёртой производной. Это делает метод очень точным, гораздо более точным, чем явный и неявный методы Эйлера, имеющие только первый порядок.
Реализация RK4
Существует уже много объяснений математики, используемой в RK4. Например: здесь, здесь и здесь. Я настоятельно рекомендую изучить его выведение и понять, как и почему он работает на математическом уровне. Но я понимаю, что целевая аудитория этой статьи — программисты, а не математики, поэтому мы здесь будем рассматривать только реализацию. Так что давайте приступим.
Прежде чем приступить, давайте зададим состояние объекта как struct в C++, чтобы можно было удобно хранить позицию и скорость в одном месте:
Также нам нужна структура для хранения производных значений состояний:
Теперь нам нужна функция для вычисления состояния физики из t в t+dt с помощью одного набора производных, а после этого для вычисления производных в новом состоянии:
Функция ускорения управляет всей симуляцией. Давайте используем её в системе пружинного амортизатора и вернём ускорение для единичной массы:
То, что нужно здесь записать, разумеется, зависит от симуляции, но необходимо структурировать симуляцию таким образом, чтобы можно было вычислять ускорение внутри этого метода для заданных состояния и времени, в противном случае он не подойдёт для интегратора RK4.
Наконец, мы получаем саму процедуру интегрирования:
Интегратор RK4 делает выборку производной в четырёх точках, чтобы определить кривизну. Заметьте, как производная a используется при вычислении b, b используется при вычислении c, и c для d. Эта передача текущей производной в вычисление следующей и даёт интегратору RK4 его точность.
Важно то, что каждая из этих производных a, b, c и d будет разной, когда темп изменения в этих величинах является функцией времени или функцией самого состояния. Например, в нашей системе пружинного амортизатора ускорение является функцией текущей позиции и скорости, которые меняются в шаге времени.
После вычисления четырёх производных наилучшая общая производная вычисляется как взвешенная сумма, полученная из разложения в ряд Тейлора. Эта комбинированная производная используется для перемещения позиции и скорости вперёд во времени, точно так же, как мы делали это в явном интеграторе Эйлера.
Сравнение симплектического метода Эйлера и RK4
Давайте подвергнем проверке интегратор RK4.
Очевидно, что поскольку он является интегратором более высокого порядка (четвёртый против первого) он наглядно будет более точен, чем симплектический метод Эйлера, правда?

Неправда. Оба интегратора так близки к точному результату, что при таком масштабе почти невозможно найти между ними разницу. Оба интегратора стабильны и очень хорошо повторяют точное решение при dt= 1 ⁄100.

При увеличении видно, что RK4 действительно более точен, чем симплектический метод Эйлера, но стоит ли эта точность сложности и лишнего времени выполнения RK4? Трудно судить.
Давайте постараемся и посмотрим, сможем ли мы найти значительное различие между двумя интеграторами. К сожалению, мы не сможем долго наблюдать за этой системой, потому что она быстро затухает до нуля, поэтому давайте перейдём к простому гармоническому осциллятору, который колеблется бесконечно и без затуханий.
Вот точный результат, к которому мы будем стремиться:

Чтобы усложнить интеграторам задачу, давайте увеличим шаг времени до 0,1 секунды.
Теперь запустим интеграторы на 90 секунд и увеличим масштаб:

Через 90 секунд симплектический метод Эйлера (оранжевая кривая) сдвинулся по фазе относительно точного решения, потому что его частота немного отличалась, в то время как зелёная кривая RK4 соответствует частоте, но теряет энергию!
Мы чётко можем это заметить, увеличив шаг времени до 0,25 секунды.
RK4 сохраняет верную частоту, но теряет энергию:

А симплектический метод Эйлера в среднем намного лучше сохраняет энергию:

Заключение
Мы реализовали три различных интегратора и сравнили результаты.
- Явный метод Эйлера
- Симплектический метод Эйлера
- Метод Рунге-Кутты порядка 4 (RK4)
Если вам действительно нужна бОльшая точность, чем у симплектического метода Эйлера, я рекомендую посмотреть на симплектические интеграторы более высокого порядка, рассчитанные на гамильтоновы системы. Таким образом вы изучите более современные техники интегрирования высокого порядка, которые лучше подходят для симуляций, чем RK4.
Читайте также:

