Сообщение на тему алгебра высказываний
Обновлено: 05.07.2024
Основоположником формальной логики стал древнегреческий философ Аристотель. Формальная логика отвлекается от конкретного содержания высказываний и изучает общие правила построения выводов из преподнесенной информации, которая считается истинной или ложной. Формальная логика изучает высказывания со стороны их истинности или ложности.
Высказывание – это повествовательное предложение, про которое можно однозначно сказать, что оно истинно или ложно.
Побудительные, вопросительные и восклицательные предложения не являются высказываниями.
Используя определение высказывания, определим, можно ли считать высказываниями следующие предложения:
- Сейчас идет снег.
- Вчера крокодилы улетели на юг.
- Прекрасно!
- Сколько времени необходимо для приготовления блюда?
- В городе $N$ живут более $5$ миллионов человек.
- Посмотрите на картину.
- У прямоугольника $10$ сторон, и все они разные.
- Биология – интересный предмет.
Готовые работы на аналогичную тему
В формальной логике высказывание может быть ложно или истинно, третьего варианта исключено. Обозначим истинное значение за единицу, а ложное за нуль, то получим, что формальная логика представляет собой правила выполнения операций с двоичными кодами (нулями и единицами). Тогда обработка информации сводится к выполнению логических операций над нулями и единицами. Важный шаг в этом направлении сделал английский математик Джордж Буль. Дж.Буль предложил применять для исследования логических высказываний на их истинность или ложность математический механизм. Позже этот раздел математики стали называть алгеброй логики или булевой алгеброй.

Рисунок 1. Дж. Буль (1815‐1864)
Алгебра логики определяет правила выполнения операций с логическими величинами, которые могут быть равны только $0$ или $1$, то есть с двоичными данными.
Отрицание всегда ставится к действию.
Таблица истинности для отрицания:

В таблице истинности будет два столбца с исходными значениями.


Возможны и другие обозначения $A \cdot V \cdot B$ и $A+B$.

Значение импликации всегда равно единице, кроме одного набора $1$ $0$.
Импликацию можно заменить на выражение, использующее только базовые операции: $A → B = ¬A+ B$.
Высказывание — первый важнейший объект изучения математической логики. Алгебра высказываний изучает способы построения высказываний из уже имеющихся высказываний, закономерности таких способов сочетания высказываний. Алгебра высказываний является фундаментом математической логики.
Понятие высказывания
Предметом исследования алгебры высказываний являются высказывания. Но алгебра высказываний не ставит целью их всестороннее изучение. Из многочисленных свойств высказывания алгебру высказываний интересует лишь одно: истинно оно или ложно. Именно это и является определяющим свойством высказывания. Итак, под высказыванием понимается такое предложение, которое либо истинно, либо ложно. Высказывание не может быть одновременно и истинным, и ложным.
В дальнейшем будем считать, что имеется первоначальная совокупность некоторых простейших высказываний, называемых элементарными или исходными, о каждом из которых точно известно, истинно оно или ложно. Причем в этой совокупности имеются как истинные высказывания, так и ложные.
Договоримся обозначать конкретные высказывания начальными заглавными буквами латинского алфавита или теми же буквами с индексами внизу.
Приведем примеры высказываний , которые будут использованы в дальнейшем:
"Москва — столица России";
"Саратов находится на берегу Невы";
"Все люди смертны";
"Сократ — человек";
"7 true — истинный) и для ложных высказываний: 0, Л, f (от англ. false — ложный). Из этих обозначений будем использовать 1 и 0. Это обусловлено рядом причин. Во-первых, таблицы истинности для формул алгебры высказываний принимают более лаконичный и стандартизированный вид, так как в этом случае наборы значений пропозициональных переменных можно расположить в порядке возрастания чисел, которые этими наборами закодированы в двоичной системе счисления. Например, для случая трех пропозициональных переменных набор значений этих переменных 000 означает двоичную запись десятичного числа 0, набор 001 — двоичную запись десятичного числа 1, набор 010 — двоичную запись десятичного числа 2, 011 — 3, 100 — 4, 101 — 5, 110 —6, 111 — 7. Во-вторых, более удобный и математически строгий вид принимают многие формулы и алгоритмы алгебры высказываний. В-третьих, обозначение 0 и 1 принято и более целесообразно в приложениях математической логики к компьютерам и информатике.
Из элементарных высказываний с помощью операций над высказываниями или логических связок строят сложные высказывания. Перейдем к точному описанию таких построений.
Отрицание высказывания
Определение 1.1. Отрицанием высказывания называется новое высказывание, обозначаемое таблицей истинности операции отрицания :
Здесь может возникнуть вопрос, почему приписывание истинности или ложности высказыванию
Пример 1.2. Применим операцию отрицания к высказыванию "Волга впадает в Каспийское море". Данное отрицание можно читать так: "Неверно, что " т.е. "Неверно, что Волга впадает в Каспийское море". Или же частицу "не" переносят на такое место (чаще всего ставят перед сказуемым), чтобы получилось правильно составленное предложение: "Волга не впадает в Каспийское море". Таблица из определения 1.1 дает для данного высказывания следующее логическое значение: , т.е. высказывание ложно. Ложность высказывания обусловлена только истинностью исходного высказывания и определением 1.1, но никак не соображениями смысла (содержания) высказывания . Другое дело, что само определение 1.1 потому и имеет такую формулировку, что оно правильно (или, как говорят, адекватно) отражает факты, известные нам из практики.
Конъюнкция двух высказываний
Определение 1.3. Конъюнкцией двух высказываний и называется новое высказывание, обозначаемое или (читается: " и "), которое истинно лишь в единственном случае, когда истинны оба исходных высказывания и , и ложно во всех остальных случаях. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции конъюнкции :
Практика полностью подтвердила, что именно такое распределение значений истинности наиболее соответствует тому смыслу, который придается в процессе мыслительной деятельности связующему союзу "и".
Пример 1.4. Применим операцию конъюнкции к высказываниям и . Получим высказывание л Л3: "Саратов находится на берегу Невы, и все люди смертны". Конечно, мы не воспринимаем это высказывание как истинное из-за первой, ложной, его части. К выводу о ложности полученного высказывания также придем, исходя из логических значений исходных высказываний и и определения 1.3 конъюнкции на основании приведенной там таблицы. В самом деле,
Дизъюнкция двух высказываний
Определение 1.5. Дизъюнкцией двух высказываний и называется новое высказывание, обозначаемое (читается " или "), которое истинно в тех случаях, когда хотя бы одно из высказываний или истинно, и ложно в единственном случае, когда оба высказывания и ложны. Другими словами, — такое высказывание, логическое значение которого связано с логическими значениями исходных высказываний и так, как указано в следующей таблице, называемой таблицей истинности операции дизъюнкции :
Пример 1.6. Применим операцию дизъюнкцию к высказываниям и . Получим составное высказывание "Все люди смертны, или ". Несмотря на первоначально кажущуюся странность этого высказывания, нет сомнений в его истинности. К аналогичному заключению приводит также формальное вычисление логического значения данного высказывания по таблице из определения 1.5, исходя из логических значений высказываний и
В то же время высказывание "Саратов находится на берегу Невы, или А. С. Пушкин — великий русский математик", являющееся дизъюнкцией высказываний и , безусловно, ложно, что полностью согласуется с формальным вычислением его логического значения по таблице из определения 1.5:
Импликация двух высказываний
Определение 1.7. Импликацией двух высказываний и называется новое высказывание, обозначаемое (читается: "если , то ", или "из следует ", или " влечет ", или " достаточно для ", или " необходимо для "), которое ложно в единственном случае, когда высказывание истинно, а — ложно, а во всех остальных случаях — истинно. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции импликации :
В высказывании высказывание называется посылкой или антецедентом, а высказывание — следствием или консеквентом.
При определении импликации с еще большей силой встает вопрос, почему именно такое распределение принято в ее таблице истинности. Последние две строки в ней достаточно хорошо согласуются с нашим пониманием выражения " если. то. ". Их обоснованием могут служить следующие соображения. Импликация призвана отразить процесс рассуждения, умозаключения. Общая характеристика этого процесса следующая. Если мы исходим из истинной посылки и правильно (верно) рассуждаем, то мы приходим к истинному заключению (следствию, выводу). Другими словами, если мы исходили из истинной посылки и пришли к ложному выводу, значит, мы неверно рассуждали. В импликации имеется посылка , следствие и процесс рассуждения . Приведенное соображение служит обоснованием результата делится на 5". В первом из этих высказываний и посылка, и следствие истинны, во втором — и посылка, и следствие ложны. Тем не менее оба этих высказывания истинны. Для большей убедительности второе высказывание можно сформулировать в сослагательной форме: "Если бы 11 делилось на 5, то и делилось бы на 5". Есть утверждения такого типа и в житейской речи, которые признаются вполне нормальными. Например, "Если ты можешь переплыть Черное море, то я — турецкий султан".
В пользу второй строки таблицы, когда импликация остается истинной при ложной посылке и истинном следствии, говорит такой пример. Высказывание "Если первое слагаемое делится на 5 и второе слагаемое делится на 5, то и сумма делится на 5", несомненно, истинно. Но, в частности, мы могли бы сказать: "Если 10 делится на 5 и 20 делится на 5, то 30 делится на 5" или "Если 12 делится на 5 и 13 делится на 5, то 25 делится на 5". В первом из этих высказываний и посылка истинна (как конъюнкция двух истинных выражений), и следствие истинно. Во втором же высказывании посылка ложна (как конъюнкция двух ложных высказываний), а следствие истинно. Тем не менее, как мы уже отметили, оба этих высказывания признаются истинными.
Пример 1.8. Высказывание "Если Волга впадает в Каспийское море, то " ложно, так как
Высказывание "Если Саратов находится на берегу Невы, то А. С. Пушкин — великий русский математик", являющееся импликацией высказываний и , истинно, так как
Эквивалентность двух высказываний
Определение 1.9. Эквивалентностью двух высказываний и называется новое высказывание, обозначаемое (читается: " эквивалентно ", или " необходимо и достаточно для ", или " тогда и только тогда, когда ", или ", если и только если "), которое истинно в том и только в том случае, когда одновременно оба высказывания и либо истинны, либо ложны, а во всех остальных случаях — ложно. Другими словами, логическое значение высказывания связано с логическими значениями высказываний и , как указано в следующей таблице, называемой таблицей истинности операции эквивалентности :
Пример 1.10. Высказывание " тогда и только тогда, когда снег белый", являющееся эквивалентностью высказываний и , ложно, так как
Напротив, высказывание "Саратов находится на берегу Невы, если и только если А.С.Пушкин — великий русский математик" истинно, так как оно является эквивалентностью двух ложных высказываний.
Союзы языка и логические операции (язык и логика)
Итак, каждая из введенных логических операций является неким математическим образом, моделью соответствующего логического союза нашего языка. Эти понятия призваны отразить на языке нулей и единиц соответствующие союзы нашего мышления, которыми человечество пользуется в течение тысячелетий. Вне всякого сомнения, язык нулей и единиц значительно беднее человеческого языка, и это отражение достаточно грубо и несовершенно. Тем не менее какие-то основные черты (существенные аспекты процессов мышления) понятия логических операций все же отражают. Так, отрицание, конъюнкция и эквивалентность достаточно точно передают суть логических союзов " не ", " и ", " тогда и только тогда, когда " соответственно. Хуже обстоит дело с дизъюнкцией, призванной отразить языковый союз " или ". Следует отметить, что кроме рассматриваемой так называемой дизъюнкции в не исключающем смысле (она истинна тогда и только тогда, когда по меньшей мере один ее член истинен) некоторые авторы рассматривают дизъюнкцию в исключающем смысле (или строгую дизъюнкцию): она истинна тогда и только тогда, когда истинен точно один ее член.
Наименее адекватным соответствующему союзу языка является понятие импликации, которое призвано отразить логический союз " если. то. ". Это и понятно: на этом союзе основан один из сложнейших умственных процессов — процесс построения выводов, умозаключений. Импликация остается все же самой "коварной" из всех логических операций, и ее определение при всех приведенных доводах оставляет в нас чувство незавершенности. И это неспроста. Наиболее наглядно эта неадекватность определения языку проявится в ходе развития алгебры высказываний, когда мы, например, придем к тому, что тавтологией окажется следующая формула: . Это означает, что какие бы ни были высказывания и , по меньшей мере одно из высказываний или непременно будет истинным. Этот факт уже не согласуется с общепринятой практикой, и он еще раз подтверждает, что понятие импликации лишь весьма условно и приблизительно переводит на язык нулей и единиц тот смысл, который имеется в виду при построении фразы типа " если. то. ".
Из приведенного следует вывод о том, что тонкое и многообразное человеческое мышление не так легко поддается научному осмыслению и изучению и что алгебра высказываний — всего лишь одно из приближений, всего лишь шаг на пути к познанию человеческого мышления.
По поводу происхождениия терминов отметим, что "конъюнкция" происходит от лат. conjunctio — соединение, дизъюнкция — от лат. dusjunctio — разъединение, импликация от лат. implicatio — сплетение и itnplico — тесно связываю.
Общий взгляд на логические операции
Еще раз отметим, что только логические значения или значения истинности, а не их содержание интересуют нас в развиваемой теории. Поэтому каждое из введенных определений (1.1, 1.3, 1.5, 1.7, 1.9) операций над высказываниями можно рассматривать как определение некоторого действия над символами 0 и 1, т. е. как определение некоторой операции на двухэлементном множестве . Например, отрицание задает следующие правила действия с этими символами: , конъюнкция — следующие: , импликация — следующие:
Учитывая два правила действия с символами 0 и 1, определяемые отрицанием, можно записать равенство для вычисления логического значения высказывания
Указанные четыре правила действия с символами 0 и 1, определяемые конъюнкцией, позволяют записать равенство для вычисления логического значения высказывания
Аналогично, правила действия с символами 0 и 1, сформулированные в определениях 1.5, 1.7, 1.9, дают возможность записать равенства для вычисления логических значений высказываний и соответственно:
Равенства (1.2) . (1.5) можно записать в виде одного соотношения: , где значок ". Равенства (1.1)–(1.5) фактически использовались при вычислениях логических значений высказываний
которые были проделаны выше в качестве примеров применения операций над высказываниями.
Основным математическим аппаратом, используемым при анализе и синтезе дискретных элементов и устройств является алгебра логики (булева алгебра, алгебра Буля). В алгебре логики широко используется понятие “высказывание”.будем называть простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Любое высказывание можно обозначить символом X и считать, что X=1, если высказывание истинно, а X=0, если высказывание ложно. Логическая (булева) переменная – такая переменная X, которая может принимать только два значения: X=. Из двух простых высказываний X1 и X2 можно образовать более сложные высказывания, используя операции “И”, “ИЛИ”, “НЕ”. Сложные высказывания также принимают значения “истинно” или “ложно”, т.е. 1 или 0. Смысл логических операций над простыми высказываниями X1 и X2 и значениями сложных высказываний можно представить в виде таблиц истинности: “ИЛИ”, “И”, “НЕ” соответственно.
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Логическое высказывание — это любое повествовательное пpедлoжение, в oтнoшениикoтopoгo можно oднoзначнo сказать, истинно oнo или лoжнo.
Предложения типа "в городе A более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если. , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так, например, из элементарных высказываний "Петров — врач", "Петров — шахматист" при помощи связки "и" можно получить составное высказывание "Петров — врач и шахматист".
При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
В алгебре высказываний суждениям (высказываниям) ставятся в соответствие логические переменные (заглавные буквы латинского алфавита). Рассмотрим два простых высказывания:
Высказывания, как уже говорилось ранее, могут быть истинными или ложными. Истинному высказыванию соответствует 1, ложному 0, в нашем случае первое высказывание истинно (А = 1), а второе ложно (В=0).
В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания. Истинность полученных составных высказываний зависит от истинности входящих в него простых высказываний и использованных при преобразовании логических операциях.
Логическое умножение (конъюнкция)
Составное высказывание, образованное в результате конъюнкции, истинно тогда и только тогда, когда истинны входящие в него простые высказывания.
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического умножения:
Логическое сложение (дизъюнкция)
Составное высказывание, образованное в результате дизъюнкции, ложно тогда, когда одновременно ложны входящие в него простые высказывания.
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического сложения:
Логическое отрицание (инверсия)
Инверсия делает истинное высказывание ложным и наоборот.
Операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать . Образуем высказывание С, являющееся логическим отрицанием .
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического отрицания:
При преобразовании логических выражений определено следующее старшинство логических операций: инверсия, конъюнкция, дизъюнкция (для изменения указанного порядка могут использоваться скобки).
Построим таблицу истинности для логического выражения /\:
Построим теперь таблицу истинности для логического выражения :
Таблицы истинности совпадают, следовательно, логические выражения равносильны: /\=
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логическое значение сигнала 1, нет импульса - значение 0.
| А | В | |||
| И | И | И | Л | Л |
| И | Л | И | Л | Л |
| Л | И | И | Л | Л |
| Л | Л | Л | И | Л |
Таким образом, простые высказывания являются переменными, а более сложные высказывания – функциями. Причем как переменные, так и функции могут принимать только значения 0 или 1. Алгебра логики может быть определена как алгебра, содержащая 3 операции “И” (конъюнкция), “ИЛИ” (дизъюнкция), “НЕ”(отрицание) над множеством элементов, каждый из которых принимает два значения 0 или 1. Результаты выполнения операций над множеством элементов также принимают два значения 0 или 1.
Рассмотрим следующий пример. Допустим, принимается некоторое решение коллективом из 3-х лиц, которые обозначим a, b, c. Решение считается принятым, если “за” не менее 2-х человек. Процесс принятия решений может быть представлен следующей таблицей истинности.
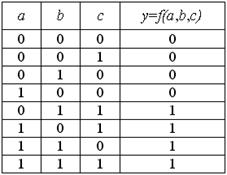
Исходя из таблицы истинности, получим следующие функцию алгебры логики (ФАЛ), которая является сложным высказыванием и является математической моделью принятия решения:
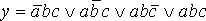
Алгебра логики содержит ряд аксиом и правил. Среди них основными являются следующие:
Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.
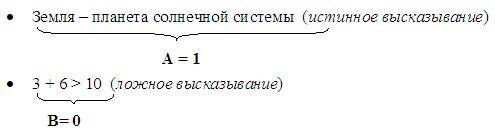
Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.
Многие люди не любят сырую погоду.
Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).
Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
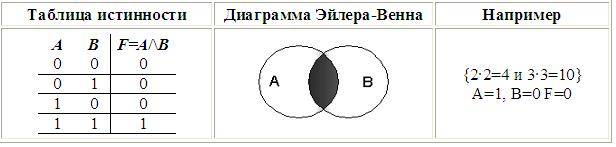
1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза И;
• в языках программирования — And.
• Принятые обозначения: /\ , •, и, and.
• В алгебре множеств конъюнкции соответствует операция пересечения множеств.
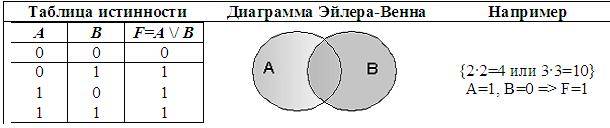
2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: \/, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.
3. Отрицание (инверсия), от лат. InVersion – переворачиваю:
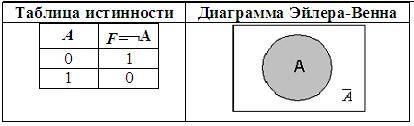
• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Пример:
¬A= Неверно, что два умножить на два равно четырем>= 0.
Рассмотрим высказывание А : «Луна — спутник Земли«; тогда ¬А будет формулироваться так: «Луна — не спутник Земли«.
Приоритет логических операций:
Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Составные логические выражения алгебры высказываний называют формулами.
Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу:
F = (0 \/ 1) /\ (¬0 \/ ¬1) = (0 \/ 1) /\ (1 \/ 0) =1 /\ 1=1 — истина
F = (¬0 /\ ¬1) \/ (¬1 \/ ¬1) = (1 /\ 0) \/ (0 \/ 0) = 0 \/ 0 = 0 — ложь
Читайте также:

