Разрешимость алгебраических уравнений сообщение
Обновлено: 01.07.2024
Не каждое алгебраическое уравнение можно решить в радикалах, т.е. выразить все его корни через коэффициенты с помощью конечной последовательности действий сложения, вычитания, умножения, деления и извлечения корня с целым показателем степени. В частности, уравнение n-ой степени с произвольными буквенными коэффициентами при n5 нельзя решить в радикалах, как установлено теоремой Руффини-Абеля.
Вместе с тем существуют отдельные классы уравнений высших степеней, которые можно решить в радикалах. Общее исследование проблем разрешимости алгебраических уравнений в радикалах является предметом важной области общей алгебры - так называемой теории Галуа (Э. Галуа ,(1811-1832)- выдающийся французский математик). Изложение этой теории выходит за пределы нашего курса. Однако один из вопросов теории разрешимости уравнений в радикалах мы в элементарной форме рассмотрим, т.к. он имеет особенное значение для курса школьной математики. Речь пойдет о разрешимости алгебраических уравнений в квадратных радикалах. Именно к этому вопросу сводится проблема разрешимости геометрических задач на построение циркулем и линейкой, в том числе широко известных классических задач: удвоения куба, трисекции угла, квадратуры круга и др.
Определение 1. Алгебраическое уравнение

f(x)= (2)
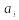
называется разрешимым в квадратных радикалах, если каждый из его корней можно представить через коэффициент (ί= 0,1,…,n) с помощью конечной последовательности действий сложения, вычитания, умножения, деления и извлечения квадратного корня.
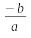
Примеры: 1. Любое линейное уравнение ax+b=0 (3) разрешимо в квадратных радикалах, т.к. его корень x= выражается через коэффициенты с помощью названных выше операций.
2. Любое квадратное уравнение ax²+bx+c=0 разрешимо в квадратных радикалах, т.к. его корни
= , =
Очевидно, что выполнение рациональных операций равносильно решению линейного уравнения ax+b=0, а извлечение квадратного корня – решению двучленного уравнения x²-a=0. Поэтому возможность решения некоторого уравнения в квадратных радикалах означает, что его можно свести к конечной цепи двучленных уравнений, степень которых не выше двух, а коэффициенты рационально выражаются через коэффициенты заданного уравнения и корни промежуточных уравнений цепи.
Связь с расширением числовых полей
Вопрос разрешимости в квадратных радикалах тесно связан с алгебраическими расширениями числовых полей.
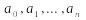
Пусть f(x)- левая часть уравнения (2)- есть многочлен над полем P. Поэтому будем считать, что P является минимальным числовым полем, которое содержит коэффициенты многочлена f(x),т.е. P=Q( ),т.к. всякое поле содержит поле Q рациональных чисел.
Определение 2. Основным полем P(или областью рациональности) уравнения =0 называется алгебраическое расширение Q( ) поля Q, образованное присоединением к нему коэффициентов данного уравнения.
Лемма. Для того чтобы уравнение (2) было разрешимо в квадратных радикалах, необходимо и достаточно, чтобы каждый из его корней можно было выразить в квадратных радикалах через некоторые числа поля P.
Доказательство: В соответствии с определением 1, уравнение (2) разрешимо в квадратных радикалах, если каждый его корень выражается в квадратных радикалах через его коэффициенты. Поэтому доказательство леммы сводится к проверке того, что некоторое число ξ выражается в квадратных радикалах через коэффициенты уравнения (2) тогда и только тогда, когда оно выражается в квадратных радикалах через некоторые числа основного поля уравнения (2).
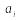
Если число ξ выражается в квадратных радикалах через коэффициенты (i= 0,1,…,n) уравнения, то тем самым оно выражается в квадратных радикалах через числа поля P=Q( ), ибо всех .
Пусть теперь, наоборот, число выражается в квадрвтных радикалах через числа поля .Каждое из чисел в свою очередь выражается рационально через некоторые рациональные числа и коэффициенты (i= 0,1,…,n) данного уравнения. Но любое рациональное число также выражается рационально через коэффициенты (i=0,1,…,n). Действительно, среди последних есть хотя бы одно число, отличное от нуля, например, 0; поэтому числа 0,1, -1, рационально выражаются через :
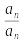
0= - ; 1= ; -1=-
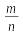
А произвольное число рационально выражается через 0,1,-1;
= при > 0 и = при 53 / 57 53 54 55 56 57 > Следующая > >>
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
называется алгебраическим уравнением n-ой степени. Число , для которого , называется корнем многочлена (6.1) или уравнения (6.2).
Теорема Гаусса(“основная теорема алгебры”). Всякий многочлен ненулевой степени имеет по крайней мере один корень (вообще говоря, комплексный).
После опубликования Гауссом в 1799 году первого доказательства этой теоремы было найдено много других, и почти все они не являются алгебраическими по сути, а используют факты и методы теории функций комплексного переменного. По этой причине название “основная теорема алгебры” не слишком удачно, к тому же оно сужает представление о современном состоянии этого раздела математики.
Далее, число является корнем многочлена в том и только том случае, когда делится без остатка на бином , т.е.
где - многочлен ( )-ой степени. Если делится без остатка на , , но не делится на , то называется корнем кратности k многочлена ; при этом
Теорема Гаусса можем быть уточнена следующим образом: многочлен
n-ой степени имеет ровно n корней, если каждый корень считать столько раз, какова его кратность.
Если коэффициенты многочлена (5.1) действительные числа и - его комплексный корень, то сопряженное число - также корень этого многочлена, причем корни и имеют одинаковую кратность.
Пусть многочлен имеет корни кратностей, соответственно, . Тогда его можно разложить на линейные множители, т.е. справедливо тождество
Если при этом коэффициенты многочлена – действительные числа, то, объединяя скобки, соответствующие комплексно сопряженным корням, можно разложить этот многочлен в произведение линейных и квадратных множителей с действительными коэффициентами.
Пример. Найти корни многочлена и разложить его на множители. Заметим, что . Поэтому корнями данного многочлена являются корни третьей степени из -1:
При этом каждый корень имеет кратность k=2 . Разложение этого многочлена на линейные множители имеет вид
Объединяя последние две скобки в один сомножитель, получим разложение на множители с действительными коэффициентами
Группа Галуа уравнения характеризует, как это видно из определения, внутреннюю симметрию корней уравнения. Оказалось, что все наиболее существенные вопросы, касающиеся возможности свести решение заданного уравнения к решению уравнений низших степеней, а также многие другие, могут быть сформулированы в виде вопросов о строении группы Галуа, а группа Галуа каждого уравнения степени есть некоторая группа подстановок степени, т. е. объект вполне конечный, все соотношения в котором, по меньшей мере теоретически, можно найти хотя бы путем проб.
Изучение группы Галуа представляет собой замечательный метод решения проблем, относящихся к алгебраическим уравнениям высших степеней. Например, можно доказать, что уравнение разрешимо в радикалах в том и только в том случае, если разрешима его группа Галуа (определение разрешимой группы см. § 3, стр. 268). Уже упоминалось,
К числу уравнений, не разрешимых в радикалах, относятся и уравнения (9) при поскольку их группа Галуа также симметрическая.
В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае. Вопрос о выводимости в формальной теории является частным, но вместе с тем, важнейшим случаем более общей проблемы разрешимости.
Содержание
История вопроса и предпосылки
Понятия алгоритма и аксиоматической системы имеют давнюю историю. И то и другое известно ещё со времён античности. Достаточно вспомнить постулаты геометрии Евклида и алгоритм нахождения наибольшего общего делителя того же Евклида. Несмотря на это, чёткого математического определения исчисления и особенно алгоритма не существовало очень долгое время. Особенность проблемы, связанной с формальным определением неразрешимости состояла в том, что для того, чтобы показать, что некоторый алгоритм существует, достаточно его просто найти и продемонстрировать. Если же алгоритм не находится, возможно его не существует и это тогда требуется строго доказать. А для этого нужно точно знать, что такое алгоритм.
Большой прогресс в формализации этих понятий был достигнут в начале XX века Гильбертом и его школой. Тогда, сначала, сформировались понятия исчисления и формального вывода, а затем Гильбертом же, в его знаменитой программе обоснования математики была поставлена амбициозная цель формализации всей математики. Это предусматривало, в том числе, возможность автоматической проверки любой математической формулы на предмет истинности. Отталкиваясь от работ Гильберта Гёдель впервые описал класс так называемых рекурсивных функций, с помощью которой доказал свои знаменитые теоремы о неполноте. Впоследствии был введён ряд других формализмов, таких как машина Тьюринга, λ-исчисление, оказавшихся эквивалентными рекурсивным функциям. В настоящее время, каждый из них считается формальным эквивалентом интуитивного понятия вычислимой функции. Эта эквивалентность постулируется тезисом Чёрча.
Когда понятия исчисления и алгоритма были уточнены, последовал ряд результатов о неразрешимости различных теорий. Одним из первых таких результатов была теорема, доказанная Новиковым, о неразрешимости проблемы слов в группах. Разрешимые же теории были известны задолго до этого.
Общие сведения
Формальное исчисление в общем случае должно определять язык, правила построения термов и формул, аксиомы и правила вывода. Таким образом, для каждой теоремы T, всегда можно построить цепочку A1, A2, … , An=T, где каждая формула Ai либо является аксиомой, либо выводима из предыдущих формул, по одному из правил вывода. Разрешимость означает, что существует алгоритм, который для каждого правильно построенного предложения T, за конечное время выдаёт однозначный ответ: да, данное предложение выводимо в рамках исчисления или нет — оно не выводимо.
Очевидно, что противоречивая теория разрешима, так как любая формула будет выводимой. С другой стороны, если исчисление не обладает рекурсивно перечислимым множеством аксиом, как например, логика второго порядка, оно, очевидно, не может быть разрешимым.
Примеры разрешимых теорий
Примеры неразрешимых теорий
Полуразрешимость и автоматическое доказательство
Разрешимость — очень сильное свойство, и большинство полезных и используемых на практике теорий им не обладают. В связи с этим было введено более слабое понятие полуразрешимости. Полуразрешимость означает наличие алгоритма, который за конечное время всегда подтвердит, что предложение истинно, если это действительно так, но если нет — может работать бесконечно.
Требование полуразрешимости эквивалентно возможности эффективно перечислить все теоремы данной теории. Иными словами, множество теорем должно быть рекурсивно-перечислимым. Такая процедура для логики первого порядка была описана ещё Гильбертом. На самом деле, теория будет полуразрешимой, если множество её аксиом и правил вывода будут рекурсивными перечислимыми множествами. Большинство, используемых на практике теорий, удовлетворяют этому требованию.
Большое практическое значение имеют эффективные полуразрешающие процедуры для логики первого порядка, так как они позволяют (полу)автоматически доказывать формализованные утверждения очень широкого класса. Прорывом в этой области было открытие Робинсоном в 1965 году метода резолюций. Другим важнейшим полуразрешающим алгоритмом на сегодняшний день является табло-метод.
Связь разрешимости и полноты
В математической логике, традиционно используется два понятия полноты: собственно полнота и полнота, относительно некоторого класса интерпретаций (или структур). В первом случае, теория полна, если любое предложение в ней является либо истинным, либо ложным. Во втором — если любое предложение, истинное при всех интерпретациях из данного класса выводимо. Например, натуральная арифметика неполна, согласно теоремам Гёделя о неполноте, но она полна относительно своей стандартной интерпретации — это следует из теоремы Гёделя о полноте.
Оба понятия тесно связанны с разрешимостью. Например, если множество аксиом полной теории первого порядка рекурсивно перечислимо, то она разрешима. Это следует из известной теоремы Поста, утверждающей, что если множество и его дополнение оба рекурсивно перечислимы то они также рекурсивны. Интуитивно, аргумент, показывающий истинность приведённого утверждения следующий: если теория полна, и множество её аксиом рекурсивно перечислимо, то существуют полуразрешающие процедуры, для проверки истинности любого утверждения, равно как и его отрицания. Если запустить обе эти процедуры параллельно, то учитывая полноту теории, одна из них должна когда-нибудь остановиться и выдать позитивный ответ.
Если теория полна, относительно некоторого класса интерпретаций, это можно использовать для построения разрешающей процедуры. Например пропозициональная логика полна относительно интерпретации на таблицах истинности. Поэтому построение таблицы истинности по данной формуле будет примером разрешающего алгоритма для пропозициональной логики.
Читайте также:

