Применение логарифмической функции сообщение

Обновлено: 04.07.2024

ЛОГАРИФМ, число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление – вычитанием, возведение в степень – умножением и извлечение корней – делением.

Общее описание.

Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (10 2 = 100). Если n – заданное число, b – основание и l – логарифм, то b l = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений log_b n = l и antilog_b l = n.

Основные свойства логарифмов:

Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b и n – рациональные числа, то в редких случаях найдется такое рациональное число l, что b l = n. Однако можно определить иррациональное число l, например, такое, что 10 l = 2; это иррациональное число l можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e, трансцендентному числу, приближенно равному 2,71828, называются натуральными логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e 0,6931 = 2. См. также ЧИСЛО e.

Пользование таблицами обычных логарифмов.

Обычный логарифм числа – это показатель степени, в которую нужно возвести 10, чтобы получить данное число. Так как 10 0 = 1, 10 1 = 10 и 10 2 = 100, мы сразу получаем, что log1 = 0, log10 = 1, log100 = 2 и т.д. для возрастающих целых степеней 10. Аналогично, 10 –1 = 0,1, 10 –2 = 0,01 и, следовательно, log0,1 = –1, log0,01 = –2 и т.д. для всех целых отрицательных степеней 10. Обычные логарифмы остальных чисел заключены между логарифмами ближайших к ним целых степеней числа 10; log2 должен быть заключен между 0 и 1, log20 – между 1 и 2, а log0,2 – между -1 и 0. Таким образом, логарифм состоит из двух частей, целого числа и десятичной дроби, заключенной между 0 и 1. Целочисленная часть называется характеристикой логарифма и определяется по самому числу, дробная часть называется мантиссой и может быть найдена из таблиц. Кроме того, log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Логарифм числа 2 равен 0,3010, поэтому log20 = 0,3010 + 1 = 1,3010. Аналогично, log0,2 = log(2ё10) = log2 – log10 = (log2) – 1 = 0,3010 – 1. Выполнив вычитание, мы получим log0,2 = – 0,6990. Однако удобнее представить log0,2 в виде 0,3010 – 1 или как 9,3010 – 10; можно сформулировать и общее правило: все числа, получающиеся из данного числа умножением на степень числа 10, имеют одинаковые мантиссы, равные мантиссе заданного числа. В большинстве таблиц приведены мантиссы чисел, лежащих в интервале от 1 до 10, поскольку мантиссы всех остальных чисел могут быть получены из приведенных в таблице.

В большинстве таблиц логарифмы даются с четырьмя или пятью десятичными знаками, хотя существуют семизначные таблицы и таблицы с еще бóльшим числом знаков. Научиться пользоваться такими таблицами легче всего на примерах. Чтобы найти log3,59, прежде всего заметим, что число 3,59 заключено между 10 0 и 10 1 , поэтому его характеристика равна 0. Находим в таблице число 35 (слева) и движемся по строке до столбца, у которого сверху стоит число 9; на пересечении этого столбца и строки 35 стоит число 5551, поэтому log3,59 = 0,5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, необходимо прибегнуть к интерполяции. В некоторых таблицах интерполирование облегчается пропорциональными частями, приведенными в последних девяти столбцах в правой части каждой страницы таблиц. Найдем теперь log736,4; число 736,4 лежит между 10 2 и 10 3 , поэтому характеристика его логарифма равна 2. В таблице находим строку, слева от которой стоит 73 и столбец 6. На пересечении этой строки и этого столбца стоит число 8669. Среди линейных частей находим столбец 4. На пересечении строки 73 и столбца 4 стоит число 2. Прибавив 2 к 8669, получим мантиссу – она равна 8671. Таким образом, log736,4 = 2,8671.

Натуральные логарифмы.

Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 – log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10ґ54,32 = 10 2 ґ5,432. Таким образом, по натуральному логарифму данного числа a можно найти натуральные логарифмы чисел, равные произведениям числа a на любые степени n числа 10, если к lna прибавлять ln10, умноженный на n, т.е. ln(aґ10 n ) = lna + nln10 = lna + 2,3026n. Например, ln0,005432 = ln(5,432ґ10 –3 ) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x = lny, то y = e x , и y называется экспонентой от x (для удобства типографского набора часто пишут y = exp x). Экспонента играет роль антилогарифма числа x.

С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e. Если log_b a = x, то b x = a, и, следовательно, log_c b x = log_c a или xlog_c b = log_c a, или x = log_c a/log_c b = log_b a. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c можно построить таблицы логарифмов по любому другому основанию b. Множитель 1/log_c b называется модулем перехода от основания c к основанию b. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = log_e 5,432/log_e 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.

Специальные таблицы.

Первоначально логарифмы были изобретены для того, чтобы, пользуясь их свойствами logab = loga + logb и loga/b = loga – logb, превращать произведения в суммы, а частные в разности. Иначе говоря, если loga и logb известны, то с помощью сложения и вычитания мы легко можем найти логарифм произведения и частного. В астрономии, однако, часто по заданным значениям loga и logb требуется найти log(a + b) или log(a – b). Разумеется, можно было бы сначала по таблицам логарифмов найти a и b, затем выполнить указанное сложение или вычитание и, снова обратившись к таблицам, найти требуемые логарифмы, но такая процедура потребовала бы трехкратного обращения к таблицам. З.Леонелли в 1802 опубликовал таблицы т.н. гауссовых логарифмов – логарифмов сложения сумм и разностей – позволявшие ограничиться одним обращением к таблицам.

В 1624 И.Кеплером были предложены таблицы пропорциональных логарифмов, т.е. логарифмов чисел a/x, где a – некоторая положительная постоянная величина. Эти таблицы используются преимущественно астрономами и навигаторами.

Пропорциональные логарифмы при a = 1 называются кологарифмами и применяются в вычислениях, когда приходится иметь дело с произведениями и частными. Кологарифм числа n равен логарифму обратного числа; т.е. cologn = log1/n = – logn. Если log2 = 0,3010, то colog2 = – 0,3010 = 0,6990 – 1. Преимущество использования кологарифмов состоит в том, что при вычислении значения логарифма выражений вида pq/r тройная сумма положительных десятичных долей logp + logq + cologr находится легче, чем смешанная сумма и разность logp + logq – logr.

История.

Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287–212 до н.э.) воспользовался степенями числа 10 8 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М.Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:

Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.

поэтому таблицы Нейпера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 – 10 –7 )ґ10 7 , приближенно равное 1/e.

Независимо от Нейпера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий. Это были таблицы антилогарифмов по основанию (1 + 10 –4 ) ґ10 4 , достаточно хорошему приближению числа e.

Логарифмическая функция.

Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы – в геометрической, представлен на рис. 2,а. График обратной, или показательной (экспоненциальной), функции y = e x , ординаты которого возрастают в геометрической прогрессии, а абсциссы – в арифметической, представлен, соответственно, на рис. 2,б. (Кривые y = logx и y = 10 x по форме аналогичны кривым y = lnx и y = e x .) Были предложены также альтернативные определения логарифмической функции, например,

Благодаря работам Эйлера стали известны соотношения между логарифмами и тригонометрическими функциями в комплексной плоскости. Исходя из тождества e ix = cos x + i sin x (где угол x измеряется в радианах, ), Эйлер заключил, что каждое отличное от нуля действительное число имеет бесконечно много натуральных логарифмов; все они являются комплексными в случае отрицательных чисел и все, кроме одного, – в случае положительных чисел. Поскольку e ix = 1 не только при x = 0, но и при x = ± 2kp, где k – любое положительное целое число, за натуральный логарифм числа 1 можно принять любое из чисел 0 ± 2kpi; и, аналогично, натуральные логарифмы числа -1 являются комплексными числами вида (2k + 1)pi, где k – целое число. Аналогичные утверждения справедливы и относительно общих логарифмов или других систем логарифмов. Кроме того, определение логарифмов можно обобщить, пользуясь тождествами Эйлера так, чтобы оно включало комплексные логарифмы комплексных чисел.

Альтернативное определение логарифмической функции дает функциональный анализ. Если f (x) – непрерывная функция действительного числа x, обладающая следующими тремя свойствами: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), то f (x) определяется как логарифм числа x по основанию b. Это определение обладает рядом преимуществ перед определением, приведенным в начале этой статьи.

Приложения.

Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных. Вычисление произведений, частных, степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов, но и благодаря использованию т.н. логарифмической линейки – вычислительного инструмента, принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами, т.е. расстояние от числа 1 до любого числа x выбрано равным log x; сдвигая одну шкалу относительно другой, можно откладывать суммы или разности логарифмов, что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков (бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y = kx n , то ее логарифмический график имеет вид прямой, т.к. log y = log k + n log x – уравнение, линейное относительно log y и log x. Наоборот, если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой, то эта зависимость – степенная. Полулогарифмическая бумага (у которой ось ординат имеет логарифмическую шкалу, а ось абсцисс – равномерную шкалу) удобна в тех случаях, когда требуется идентифицировать экспоненциальные функции. Уравнения вида y = kb rx возникают всякий раз, когда некая величина, такая как численность населения, количество радиоактивного материала или банковский баланс, убывает или возрастает со скоростью, пропорциональной имеющемуся в данный момент количеству жителей, радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу, то график будет иметь вид прямой.

Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой, известной под названием логарифмической спирали, потому что в полярной системе координат ее уравнение имеет вид r = ae bq , или lnr = lna + bq. Такую кривую описывает движущаяся точка, расстояние от полюса которой растет в геометрической прогрессии, а угол, описываемый ее радиусом-вектором – в арифметической. Повсеместность такой кривой, а следовательно и логарифмической функции, хорошо иллюстрируется тем, что она возникает в столь далеких и совершенно различных областях, как контур кулачка-эксцентрика и траектория некоторых насекомых, летящих на свет.

Логарифмическая спираль - плоская кривая, описываемая точкой, движущейся по прямой, которая вращается около одной из своих точек (полюса) так, что логарифм расстояния движущейся точки от полюса изменяется пропорционально углу поворота. Спираль эта имеет бесконечное множество витков и при раскручивании и при скручивании. Последнее означает, что она не проходит через свой полюс. Логарифмическую спираль еще называют равноугольной спиралью, потому что в любой ее точке угол между касательной и к ней и радиус – вектором сохраняет постоянное значение.

Применение логарифмической функции

Введение В школьном курсе логарифм опосредованно, изучается используется только для решения уравнений К сожалению, не даётся полная его информация мере применения. углубления в изучение логарифма открывается широкое проникновение различные спектры жизни. о широте Но его в и неравенств. по

Применение логарифмической функции

Из истории логарифмов логарифм происходит от греческого (число) и (отношение), и переводится как отношение чисел. Джон Непер что логарифмы возникли при сопоставлении двух чисел, одно из которых членом является арифметической прогрессии, а геометрической. объяснял, Слово другое

Применение логарифмической функции

Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в точке каждой с радиус- образовывала вектором в каждой точке один и тот же угол. Он показал, что это условие равносильно тому, углы для что полярные точек кривой пропорциональны логари фмам радиус-векторов.

Применение логарифмической функции

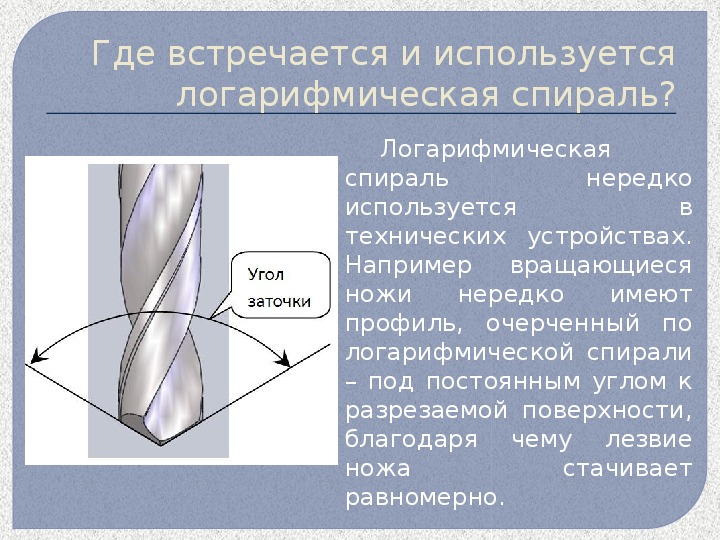
Где встречается и используется логарифмическая спираль? Логарифмическая нередко нередко спираль в используется технических устройствах. Например вращающиеся ножи имеют профиль, очерченный по логарифмической спирали – под постоянным углом к разрезаемой поверхности, благодаря чему лезвие ножа стачивает равномерно.

Применение логарифмической функции

Логарифмическая спираль в природе Раковины в морских животных могут расти лишь одном направлении. Чтобы не слишком вытягиваться приходиться им скручиваться, причём следующий каждый виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать что эта спираль является математическим символом соотношения

Применение логарифмической функции

Поэтому Логарифмическая спираль в природе раковины многих моллюсков, улиток, а так же рога млекопитающих таких как (горные козлы), закручены по логарифмической спирали. подсолнухе расположены по дугам, так же к логарифмической спирали. Семечки архары в близким

Применение логарифмической функции

Логарифмическая спираль в природе наиболее из Один распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали. По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.

Применение логарифмической функции

Пример Самолёт взлетевший из какой – нибудь точки земного шара на север, через некоторое время окажется над Северным полюсом. Если же он полетит на восток, то облетев параллель, вернётся в тот же пункт, из которого вылетел. Предположим теперь, что самолёт будет лететь пересекая все меридианы под одним и тем же углом, отличным от прямого, т.е. держась всё время одного и того же курса. Когда он облетит земной шар, то попадёт в точку имеющую ту же долготу, что и точка вылета, но расположенную ближе к Северному полюсу. После следующего облёта он окажется ещё ближе к полюсу и продолжая лететь указанным образом, будет описывать вокруг полюса сужающуюся спираль.

Мы все знакомы с основными арифметическими действиями: сложением, вычитанием, умножением и делением. Пятым арифметическим действием является возведение в степень. Возведение в степень имеет два обратных действия: извлечение корня и логарифмирование.

Логарифмы появились в ХVI в. под влиянием все возрастающих потребностей практики как средство для упрощения вычислений. Их изобретение тесно связано с развитием в XVI веке производства и торговли, астрономии и мореплавания, требовавших усовершенствования методов вычислительной математики. Все чаще требовалось производить громоздкие действия над многозначными числами, все точнее и точнее должны быть результаты действий. Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов, удлинило, по выражению Лапласа, жизнь вычислителей.

Логарифмы необычайно быстро вошли в практику. Было создано практическое средство - таблицы логарифмов, резко повысившее производительность труда вычислителей. Уже в 1623 г. английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.

Математики, выделяя самые существенные черты того или иного наблюдаемого в природе явления, вводя числовые характеристики и связывая эмпирические данные с помощью различных математических зависимостей, тем самым составляют математическую модель явления. При составлении модели того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль.

Логарифмическая спираль – это линии в геометрии, отличные от прямых и окружностей, которые могут скользить по себе. Логарифмическую спираль называют равноугольной спиралью. Логарифмическая спираль знаменита и своими удивительными свойствами:

1. Она остается неизменной не только при преобразовании подобия, но и при других различных преобразованиях.

2. Логарифмическая спираль пересекает свои радиус-векторы под постоянным углом. В любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение. На основании этого ее называют равноугольной.

3. Последнее свойство находит свое применение в технике. В технике часто применяются вращающиеся ножи. Сила, с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала.

Логарифмическая спираль является спиралью, которая наиболее часто встречается в природе.

1. Известно, что живые существа обычно растут, сохраняя общее начертание своей формы. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться им приходиться скручиваться, причём каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать, что эта спираль является математическим символом соотношения форм роста. Поэтому раковины многих моллюсков, улиток, а так же рога таких млекопитающих как архары, закручены по логарифмической спирали. "Никогда еще в природе не существовало столь совершенного примера логарифмических спиралей, чем начертания рога носорога". Рога горного барана, клюв попугая может расти лишь по логарифмической спирали или ее некоторым пространственным аналогам

2. Семечки в подсолнухе расположены по дугам, так же близким к логарифмической спирали.

3. Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали

4. Цепочки молекулы ДНК закручены по логарифмической спирали. Молекулы ДНК имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль.

5. По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.

7. Траектории насекомых, летящих на свет, также описывают логарифмическую спираль

8. Траектория движения разбегающегося испуганного стада северных оленей напоминает логарифмическую спираль

9. В гидротехнике по логарифмической спирали изгибают трубу, проводящую поток воды к лопастям турбины. Благодаря такой форме трубы потери энергии на изменение направления течения в трубе оказываются минимальными, и напор воды используется с максимальной производительностью.

В заключение работы можем сказать, что мы не исчерпали всех примеров применения логарифмов, так как сделать это очень сложно. Логарифмы находят самое широкое применение при обработке результатов тестирования в психологии и социологии, в составлении прогнозов погоды и даже в музыке, а также других областях науки и техники. Главное мы достигли поставленной цели и поняли, как широко применяются знания логарифмов, а главное, что не зря мы их изучаем.

1. Виленкин Н.Я. Алгебра и математический анализ.- М.:Мнемозина,2004

Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.

Логарифмы вокруг нас Пустынникова Ирина

На протяжении 16 века быстро возрастало количество приближенных вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.

С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.

Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.

Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Генри Бригс, Эдмунд Уингейт, Уильям Отред, Н. Меркатор, Джон Спейдел, К. Бремикер, Ф. Клейн.

Анализ тематики создание логарифмов достаточно актуален и представляет научный и практический интерес.

Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.

Задача: 1. Актуализация практической значимости математических знаний;

2. Развитие нравственных представлений о природе математики, сущности и происхождении математической абстракции.

Проблема: показать практическую значимость логарифмов для окружения.

Основная часть

История логарифма

Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.

В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое, сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.

Сочинение было разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой. Более развёрнутое, описание содержалось в другом труде, изданном посмертно его сыном; там же Непер пояснил, как он составлял свои таблицы.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом.

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1615 году в беседе с профессором математики Грешем Колледжа в Лондоне Генри Бригсом (1561-1631) Непер предложил принять за логарифм единицы нуль, а за логарифм десяти - 100, или, что сводится к тому же, просто 1. Так появились десятичные логарифмы и были напечатаны первые логарифмические таблицы. Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617).

Позже таблицы Бригса дополнил голландский книготорговец и любитель математики Андриан Флакк (1600-1667). Непер и Бригс, хотя пришли к логарифмам раньше всех, опубликовали свои таблицы позже других - в 1620 году.

Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега́ появилось только в 1857 году в Берлине (таблицы Бремивера).

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Знаки log и Log были введены в 1624 году И. Кеплером.

На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).

Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом.

С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов.

Таким образом, прошло 394 года с тех пор, как логарифмы впервые были введены (считая с 1614 г.), прежде чем математики пришли к определению понятия логарифма, которое положено теперь в основу школьного курса.

Логарифмические таблицы

Если вычислительные потребности практической жизни и технического обихода вполне обеспечиваются трех и четырехзначными таблицами то с другой стороны, к услугам теоретического исследователя имеются таблицы и с гораздо большим числом знаков, чем даже 14- значные логарифмы. Вообще говоря, логарифм в большинстве случаев есть число иррациональное и не может быть точно выражен никаким числом цифр; логарифмы большинства чисел, сколько бы знаков ни брать, выражаются лишь приближенно, тем точней, чем больше цифр в их мантиссе. Для научных работ оказывается иногда недостаточной точность 14- значных логарифмов, но среди пятисот всевозможных образов логарифмических таблиц вышедших в свет, со времени их изобретения, исследователь всегда найдет такие, которые его удовлетворяют. Например, 20- значные логарифмы чисел от 2 до1200, изданные во Франции Кале.

Для еще более ограниченной группы чисел имеются таблицы логарифмов с огромным числом десятичных знаков - настоящие логарифмические диковинки о существование которых не подозревают многие математики.

Вот эти логарифмы – исполины все они - не десятичные, а натуральные: (натуральными называются логарифмы, вычисленные не при основании 10, а при основании 2,718…, о котором у вас еще будет речь впереди. 48–значные таблицы Вольфрама для чисел до 10000; 61-значные таблицы Шарпа; 102-значные таблицы Паркхерста.

Счетная линейка

Логарифмическая спираль

Логарифмическая спираль - плоская трансцендентная кривая, уравнение которой в полярных координатах имеет вид p=a φ, a0.

Рога козлов, раковина улитки и семечки в подсолнухе закручены по логарифмической спирали

Применение логарифмов в различных сферах жизнедеятельности человека

Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле , где m₀ – где масса вещества в начальный период времени t=0, m – масса вещества в момент времени t, .
T - период полураспада. Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.

Народонаселение. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой , где N₀ – число людей при t=0, N – число людей в момент t, λ – некоторая константа.

Формула Циолковского. Эта формула, связывающая скорость ракеты V с ее массой m: , где Vr – скорость вылетающих газов, m₀ – стартовая масса ракеты. Скорость истечения газа при сгорании топлива Vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и для того чтобы достичь космической скорости, необходимо сделать большим отношение , т.е. почти всю стартовую массу отдать под топливо.

Звукоизоляция стен. Коэффициент звукоизоляции стен измеряется по формуле, где p₀ – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам. Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что и p₀ =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.

Логарифмы в музыке.

Номера клавишей рояля представляют собой логарифмы чисел – колебаний соответствующих звуков (умноженные на 12).

Мы даже можем сказать, что номер октавы представляет собой целую часть (характеристику) логарифма числа колебаний этого тона, а номер звука в данной октаве, деленный на 12 – дробную часть (мантиссу) этого логарифма.

Логарифмы в поэзии

Многообразные применения показательной (или её ещё называют, экспоненциальной) функции вдохновили английского поэта Элмера Брила на написание “Оды экспоненте”, отрывок из которой гласит:

« … Ею порождено многое из того,

Как говорили наши

Могущество ее порождений

Заранее обусловлено ее

Собственной красотой и силой,

Ибо они суть физическое воплощение

Абстрактной идеи ее.

Английские моряки любят ее и знают

Две шкалы Гунтера -

Вот чудо изобретательности.

У инженера и астронома не было

Инструмента полезнее, чем она.

Даже изящнее искусства питаются ею.

Разве музыкальная гамма не есть

Набор передовых логарифмов?

И таким образом абстрактно красивое

Стало предком одного из величайших

Логарифмы в психологии

Ощущения, воспринимаемые органами чувств человека, могут вызываться раздражениями, отличающимися друг от друга во много миллионов даже миллиардов раз. Удары молота о скользкую плиту в сто раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы раз превосходит яркость какой-нибудь слабой звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений.

Логарифмы в живописи

Логарифмические линии в природе замечают не только математики, но и художники, например, этот вопрос чрезвычайно волновал Сальвадора Дали.

“…моей навязчивой идеей, настоящей маниакальной страстью, стала картина Я. Вермера “Кружевница”, репродукция которой висела в отцовском кабинете” Сальвадор Дали

Молекула ДНК

С моей точки зрения, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы счисления. Потому что, математика повсюду. Она окружает нас и она есть в каждом предмете, что мы видим или держим в руках. Я не знала, что логарифмы так тесно связаны с нашей жизнью и являются ее неотъемлемой частью. Благодаря этому проекту, я осознала, насколько важна роль логарифмов в жизни.

Результаты исследования следующие:

1.Многие природные явления не могли быть изучены без понятия логарифма;

2.Логарифмы используются для описания природных явлений астрономами, физиками, биологами;

3.Понятие логарифма широко применяется человеком во многих науках;

4.Логарифм является инструментом для вычисления радиоактивного распада, изменения количества людей в стране, зависимости скорости ракеты от ее массы, коэффициента звукоизоляции;

5.Выяснили, что, играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах.

Список использованной литературы:

1.Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 1998;

3.Лиман М.М. Школьникам о математике и математиках.- М.:Просвещение,1981;

Читайте также: