Правильные и полуправильные многогранники сообщение

Обновлено: 19.05.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

В своей деятельности человеку повсюду приходится сталкиваться с изучением формы, размеров и взаимного расположения пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул, и строители, рассчитывающие постройку или разрушение зданий, и малыш в детском саду, строящий пирамидку из кубиков. Таким образом устроен окружающий нас мир, что ни один человек в своей жизни не обойдется без пространственного представления предметов.

Ни одни геометрические тела не обладают таким совершенством и

красотой, как правильные многогранники и сложностью своих форм, как полуправильные многогранники. Они открыли нам попытки

ученых приблизиться к тайне мировой гармонии и показали неотразимую

цель работы:

- ознакомиться с понятием правильного многогранника и полуправильного многогранника, с их видами;

- выяснение значимости понятий правильных и полуправильных многогранников в различных сферах деятельности человека.

В связи с поставленной перед собой целью необходимо было решить ряд

1) организовать поиск, изучение различных источников информации

(печатные, электронные, интернет) и отбор материала, представляющего

интерес по обозначенной теме;

2) обобщить, систематизировать, классифицировать изученныйматериал;

3.) оценить результат проделанной работы.

1. Основные понятия

Стереометрия - часть геометрии, в которой изучаются фигуры в пространстве. Стереометрия включает изучение плоскостей, объемных геометрических тел, их всевозможных сечений и комбинаций, а также измерение объемов и площадей тел.

Многогранник – поверхность, составленная из многоугольников, а также тело ограниченное такой поверхностью.

Правильным многогранником называется выпуклый многогранник, грани которого – равные правильные многоугольники, а двугранные углы при всех вершинах равны между собой. Доказано, что в каждой из вершин правильного многогранника сходится одно и то же число граней и одно и то же число ребер. Кроме того п равильный многогранник — это выпуклый многогранник с максимально возможной симметрией.

2. Тела Платона

Тела Платона - это выпуклые многогранники , все грани которых правильные многоугольники.

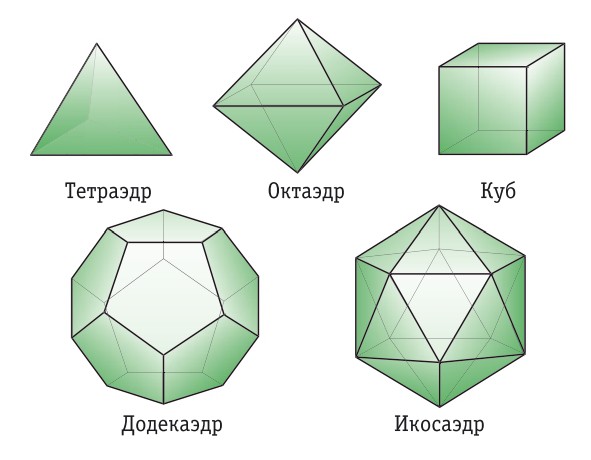
Существует всего пять правильных многогранников:

2.1. История названия правильных многогранников

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

Итак, тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань.

Гексаэдр (куб) имеет 6 граней, "гекса" – шесть.

Октаэдр - восьмигранник, "окто" – восемь.

Додекаэдр - двенадцатигранник, "додека" - двенадцать;

Икосаэдр имеет 20 граней, "икоси" - двадцать.

3. Полуправильные многогранники

Наряду с правильными многогранниками существуют еще многогранники, у которых все многогранные углы равны, а грани – правильные многоугольники нескольких видов. Они не могут быть отнесены к правильным – их называют полуправильными многогранниками.

В полуправильных многогранниках равны одноименные многоугольники; причем в каждой вершине сходится одно и тоже число одинаковых граней; в одинаковом порядке каждый из этих многогранников может быть вписан в сферу.

Конечно, возникает вопрос: сколько всего существует полуправильных многогранников? Более двух тысяч лет думали, что только тринадцать (их называют телами Архимеда, т.к. именно ему принадлежит их открытие), не считая двух бесконечных серий, составленных из призм и антипризм.

3.1. Тела Архимеда

Многогранники, у которых все многогранные углы равны, а грани -правильные, но разноименные правильные многоугольники.

Многогранники такого типа называются равноугольно полуправильными многогранниками. Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения.

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются: кубооктаэдр и икосододекаэдр

3.2 Тела Кеплера-Пуансо

Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большойзвездчатый додекаэдр и большой икосаэдр.

3.3. Тела Федорова

Федоров Евграф Степанович (22.12.1853 –21.05.1919) - русский кристаллограф, один из основоположников структурной кристаллографии и минерологи, геометр, петрограф и геолог, стал основоположником теории строения кристаллов. Его тела это выпуклые многогранники (параллелоэдры), параллельными переносами которых можно заполнить пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой (т.е. являются параллелоэдрами).Существует 5 типов Федоровых тел, найденных им в 1881г.

3.4. Каталановы тела

Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы, а каталановы - в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие пространственной симметрии.

4. Биография Платона

Платон родился в семье, имевшей аристократическое происхождение. Первым учителем Платона был Кратил. Около 407года познакомился с Сократом и стал одним из его учеников.

После смерти Сократа в 399 до н.э. уехал в Мегару.

В 389 году отправился в Южную Италию и Сицилию, где общался с пифагорейцами.

В 387 году Платон возвращается в Афины, где сновывает собственную школу — Платоновскую Академию. По древним преданиям Платон умер в день своего рождения в 347 году. По свидетельству Олимпиодора, Платон был не только философом, но и олимпийским чемпионом. Дважды он выигрывал соревнования по панкратиону — смесь бокса и борьбы.

4.2. Философия Платона

Огонь – наиболее подвижная стихия, он обладает разрушительным действием, проникая в другие тела (сжигая или расплавляя, или испаряя их); при соприкосновении с ним мы испытываем чувство боли, как если бы мы укололись или порезались. Какие частицы могли бы обусловить все эти свойства и действия? Очевидно, наиболее подвижные и легкие частицы, и притом обладающие режущими гранями и колющими углами. Из четырех многогранников, о которых может идти речь, в наибольшей степени удовлетворяет тетраэдр. Поэтому, говорит Платон, образ пирамиды (т.е. тетраэдра) и должен быть в согласии с правильным рассуждением и с правдоподобием, первоначалом и семенем огня. Наоборот, земля выступает как самая неподвижная и устойчивая из всех стихий. Поэтому частицы, из которых она состоит, должны иметь самые устойчивые основания. Из всех четырех тел этим свойством в максимальной мере обладает куб. Аналогичным образом с двумя прочими стихиями мы соотнесем частицы, обладающие промежуточными свойствами. Икосаэдр, как самый обтекаемый, представляет частичку воды, октаэдр – частицу воздуха.

1.Теория Кеплера

И.Кеплер предположил, что расстояния между орбитами планет можно получить на основании Платоновых тел, вложенных друг в друга. Результаты его расчётов хорошо согласовались с действительными расстояниями между планетными орбитами

Гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников. Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы – додекаэдр

Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.

Эта модель выглядела для своего времени довольно правдоподобно. Во-первых, расстояния, вычисленные при помощи этой модели, были достаточно близки к истинным (учитывая доступную тогда точность измерения). Во-вторых, модель Кеплера давала объяснение, почему существует только шесть (именно столько было тогда известно) планет - именно шесть планет гармонировали с пятью Платоновыми телами.

Однако даже на тот момент эта привлекательная модель имела один существенный недостаток: сам же Кеплер показал, что планеты вращаются вокруг Солнца не по окружностям ("сферам"), а по эллипсам (первый закон Кеплера). Нечего и говорить, что позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута.

Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами.

Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозоа - тетраэдр (четыре плиты) Палеозою - гексаэдр (шесть плит) Мезозою - октаэдр (восемь плит) Кайнозою - додекаэдр (двенадцать плит).

2.Многогранники в искусстве

Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Изящный пример звездчатого додекаэдра можно найти в работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.

Надгробный памятник в кафедральном соборе Солсбери.

Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.

В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.

Наш мир исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к правильным многогранникам - удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.

В моих приложениях (приложение 4) можно увидеть некоторые культурные ценности на которых изображены правильные многогранники.

(Сальвадор Дали. Тайная вечеря (1955))

3. Многогранники в природе

Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли ( NaCl ) имеют форму куба.

При производстве алюминия пользуются алюминиево-калиевыми квасцами ( K [ Al ( SO 4)2]·12 H 2 O ), монокристалл которых имеет форму правильного октаэдра.

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана ( FeS ). Кристаллы этого химического вещества имеют форму додекаэдра (см.рис.).

В разных химических реакциях применяется сурьменистый сернокислый натрий ( Na 5( SbO 4( SO 4)) – вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Последний правильный многогранник – икосаэдр передает форму кристаллов бора ( B ). В свое время бор использовался для создания полупроводников первого поколения.

Итак, благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

На микроскопическом уровне, додекаэдр и икосаэдр являются относительными параметрами ДНК, по которым построена вся жизнь. Можно увидеть также, что молекула ДНК представляет собой вращающийся куб. При повороте куба последовательно на 72 градуса по определённой модели, получается икосаэдр, который, в свою очередь, составляет пару додекаэдру. Таким образом, двойная нить спирали ДНК построена по принципу двухстороннего соответствия : заикосаэдром следует додекаэдр, затем опять икосаэдр, и так далее. Это вращение через куб создаёт молекулу ДНК.

Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на правильный двадцатигранник, или икосаэдр. Есть вирусы, размножающиеся в клетках животных (позвоночных и беспозвоночных), другие облюбова-ли растения, третьи (их называют бактериофагами или просто фагами) паразитируют в микробах, но икосаэдрическая форма вирусов сохраняется во всех трех типах вирусов.

Математики говорили, что пчелы строили шестиугольные соты задолго до появления человека. Почему пчелы строят соты именно так?

Пчелы – удивительные создания. Если разрезать пчелиные соты плоскостью, то станет видна сеть равных друг другу правильных шестиугольников. Из правильных многоугольников с одинаковой площадью наименьший периметр именно у правильных шестиугольников Стало быть, мудрые пчелы экономят воск (≈2% ) и время для постройки сот. На рисунке 1 изображена пчелиная ячейка в общем виде. На рисунке 2 можно увидеть, как соприкасаются ячейки в улье: их общая часть является ромбом.

4. Планета Земля и многогранники

- изучены информационные источники, имеющие отношение к истории возникновения и развития понятия симметрии,

- уточнены и дополнены теоретические аспекты данного понятия,

- установлена значимость и проникновение правильных многогранников в определенные области знания.

Следует отметить, что изучая информационные источники:

- я столкнулась с разнообразными видами правильных и полуправильных многогранников,

мне пришлось окунуться в мир многообразия новых для меня терминов, а так же понять, что собранные мной сведения выходят за рамки школьного курса геометрии,

- выяснила, что правильные многогранники удивительным образом связаны с мифологическими существами.

Таким образом, учитывая все законы пространства и изучив различные типы правильных многогранников можно сделать вывод, что самое прекрасное и совершенное приходит к нам от природы.

1. Атанасян, В.Ф. Бутузов, С.Б. Кардомцев и др.–5-е изд.– М.:Просвещение, 2014.

2. Лаптев Б.Л.. Н.И.Лобачевский и его геометрия. М.: Просвещение,2013.

6. Тихонов А.Н., Костомаров Д.П.. Рассказы о прикладной математике.М.: Вита-Пресс, 2016

На протяжении многих столетий человечество пополняло свои знания в разнообразных областях наук. Стереометрия – наука о пространственных фигурах – неотъемлемо связана со многими дисциплинами, такими как математика, информатика и программирование, физика, биология, химия. В архитектуре также используются теоремы и следствия стереометрии.

Многогранники изучаются школьниками в 10-11 классах. Задания, связанные с правильными и полуправильными многогранниками, вызывают наибольшую трудность у ребят, особенно задачи на построение сечений. Знания об этих пространственных фигурах пригодятся на экзамене.

Многогранники имеют богатую историю, и всё же они включены в современный раздел математики. Теория многогранников имеет большое значение не только для теоретических исследований по геометрии, но и для областей прикладной математики – линейного программирования, теории оптимального управления и др. Наиболее необычными, интересными, гармоничными и красивейшими формами обладают правильные, полуправильные и звёздчатые многогранники.

Объект исследования – многогранники.

Работа состоит из введения, двух частей и заключения.

Список использованных источников включает 25 наименований.

Теоретическая часть 1. История многогранников

Знания о многогранниках применялись ещё с древнейших времён цивилизаций Египта, Месопотамии, Африки: например, были найдены ювелирные украшения в форме многогранников, а их возраст насчитывает несколько тысяч лет, а также игральные кости (археологами была найдена игральная кость в форме додекаэдра, датируемая 1000 годом до н. э.).

Пифагор Самосский (около 582 года до н. э. – 507 год до н. э.) создал космологическое учение, связавшее правильные многогранники с устройством Вселенной. Пифагорейцы считали, что элементы первооснов бытия имеют форму правильных многогранников, а именно: огонь – тетраэдр, земля – гексаэдр, воздух – октаэдр, вода – икосаэдр. Вся Вселенная, по мнению древних, имела форму додекаэдра [10].

Иоганн Кеплер в своей работе "Тайна мироздания" в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы [6].

В 1854 году Артур Кэли дал имена двум многогранникам Кеплера (что пытался описать звёздчатые многогранники): малый звёздчатый додекаэдр и большой звёздчатый додекаэдр. Луи Пуансо обнаружил ещё два новых: большой додекаэдр и большой икосаэдр. В 1812 году Огюстен Луи Коши смог доказать гипотезу Пуансо о том, что существуют только 4 единственно возможных правильных звёздчатых многогранника (4 многогранника Кеплера-Пуансо) [3].

2. Определения многогранника, многогранной поверхности, развёртки многогранника и его элементов (рёбер, граней, вершин, двугранных углов и диагоналей)

Существуют различные определения понятия многогранник, которые можно встретить в известных учебниках.

Ж. Адамар называет многогранником тело, ограниченное со всех сторон плоскостями [1].

Многогранник имеет рёбра, грани, вершины, двугранные углы и диагонали, определения которых можно увидеть в учебниках А. П. Киселева и А. Ю. Калинина [14, 13]:

Общие стороны смежных многоугольников называются рёбрами многогранника.

Многоугольники, которые ограничивают многогранник, называются его гранями.

Грани многогранника, сходящиеся в одной точке, образуют двугранный угол;

Вершины таких многогранных углов называются вершинами многогранника.

Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями этого многогранника.

Многогранной поверхностью называется поверхность, составленная из многоугольников. Процесс составления многогранной поверхности из многоугольников можно представить себе как операцию склеивания этой поверхности из многоугольников [15].

3. Теорема Эйлера

Теорему Эйлера историки математики называют первой теоремой топологии – раздела геометрии, который изучает свойства фигур, не меняющихся при непрерывных деформациях, допускающих любые растяжения и сжатия, но без разрывов или дополнительных склеек. Соотношение Эйлера

для выпуклых многогранников является как раз таким топологическим свойством [20]. Сформулируем и докажем данную теорему Эйлера:

Теорема 1. Для любого выпуклого многогранника сумма числа его вершин В и числа его граней Г без числа рёбер Р равна двум, т. е.

Доказательство [22]. Представим поверхность данного многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим сетку (рис. 1, а), содержащую Г' = Г – 1 многоугольников (которые по-прежнему будут называться гранями), В вершин и Р рёбер.

Если для этой сетки выполняется соотношение

То для исходного многогранника будет справедливо требуемое соотношение (*).

Покажем, что требуемое соотношение (**) не изменится, если в каком-нибудь многоугольнике сетки провести диагональ. Действительно, после проведения такой диагонали в сетке будет В вершин, Р + 1 рёбер и Г' + 1 граней, и, следовательно,

Пользуясь этим свойством, проведём в сетке диагонали, разбивающие входящие в неё многоугольники на треугольники (рис. 1, б), и для полученной сетки покажем выполнимость соотношения (**). Для этого будем последовательно убирать внешние рёбра сетки, уменьшая в ней количество треугольников.

При этом возможны два случая:

а) для удаления треугольника АВС требуется снять два ребра, в нашем случае АВ и ВС;

б) для удаления треугольника MKN требуется снять одно ребро, в нашем случае MN.

В обоих случаях соотношение (**) не изменится. Например, в первом случае после удаления треугольника сетка будет состоять из В – 1 вершин,

Таким образом, удаление одного треугольника не меняет соотношение (**). Продолжая этот процесс удаления треугольников, в конце концов мы придём к сетке, состоящей из одного треугольника. Для такой сетки В = 3,

Р = 3, Г' = 1, и, следовательно, В – Р + Г' = 1. Значит соотношение (**) имеет место и для исходной сетки, откуда окончательно получаем, что для данного многогранника справедливо соотношение (*).

4. Правильные многогранники 4.1. Теорема о существовании пяти правильных многогранников

Многогранник называется выпуклым, если он лежит с одной стороны от плоскости любой своей грани, т. е. плоскость его любой грани является его опорной плоскостью [2].

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и, кроме того, в каждой его вершине сходится одно и то же число рёбер [5].

Многогранник называется правильным, если [19]:

1) все его грани равны и правильны;

2) все его многогранные углы равны и правильны.

Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще

n-угольники при . Каждая вершина правильного многоугольника может быть вершиной любо трёх, четырёх или пяти равносторонних треугольников, либо трёх квадратов, либо трёх правильных пятиугольников

Доказательство [5]. В самом деле, угол правильного n-угольника при n не меньше 120. С другой стороны, при каждой вершине многогранника должно быть не менее трёх плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные

n-угольники при n, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 120. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше .

Рассмотрим важную теорему о существовании ровно пяти правильных многогранников:

Теорема 2. Существует только пять видов правильных многогранников.

При этом мы относим к одному виду те многогранники, у которых многогранные углы имеют одно и то же число рёбер, а грани – одно и то же число сторон.

Доказательство [1]. Пусть m – число сторон каждой грани правильного многогранника; n – число рёбер каждого многогранного угла.

Если принять прямой угол за единицу, то каждый угол какой-либо грани выразится числом ; но сумма n плоских углов, примыкающих к одной вершине, должна быть меньше четырёх прямых; следовательно, каждый из них должен быть меньше .

Причём равенство исключено.

Это неравенство и даёт искомое решение. Действительно, каждое из чисел m и n больше или равно 3, но оба они не могут быть больше 3; так как для и , имеем .

Следовательно, по крайней мере одно из чисел m и n равно 3. Допустим, что это будетm: в равенстве (1) можно переставить числа m и n, так как оно симметрично относительно этих двух чисел.

При этом будем иметь:

Следовательно, n может иметь только значения 3, 4 и 5.

Симметрия неравенства (1) относительно чисел mи n не должна нас удивлять; в самом деле, каждое из этих чисел становится на место другого, если от некоторого многогранника перейти к многограннику, ему сопряжённому. Каждый раз, как m и n будут различны, мы будем иметь пару сопряжённых решений – всего-навсего получим следующие пять решений:

В соответствие с теоремой получаем следующие правильные многогранники (Платоновы тела): тетраэдр, куб, октаэдр, додекаэдр, икосаэдр (табл. 1).

В стереометрии появляется новый вид взаимного расположения прямых:

скрещивающиеся прямые (например дорога на мосту и под мостом, то есть они не пересекаются).

Ни одни геометрические тела не обладают таким совершенством и

ученых приблизиться к тайне мировой гармонии и показали неотразимую

Мной был изучен необходимый непрограммный материал, и захотелось расширить свои знания и представления по данной теме.

Предложенная тема предположила цель работы:

- ознакомиться с понятием правильного многогранника и полуправильного многогранника, с их видами;

- развитие пространственного мышления, умения обобщать и анализировать новый материал;

В связи с поставленной перед собой целью необходимо было решить ряд

1) организовать поиск, изучение различных источников информации

(печатные, электронные, интернет) и отбор материала, представляющего

интерес по обозначенной теме;

2) обобщить, систематизировать, классифицировать изученный материал;

3.) оценить результат проделанной работы.

Практическая значимость реферата:

Представить ценность данного материала в обычной жизни каждого человека.

1. Основные понятия.

Многогранник – поверхность, составленная из многоугольников, а также тело ограниченное такой поверхностью.

Правильным многогранником называется выпуклый многогранник, грани которого – равные правильные многоугольники, а двугранные углы при всех вершинах равны между собой. Доказано, что в каждой из вершин правильного многогранника сходится одно и то же число граней и одно и то же число ребер. Кроме того правильный многогранник, или Платоново тело — это выпуклый многогранник с максимально возможной симметрией.

Иоганн Кеплер называл куб "родителем" всех правильных многогранников. На основе куба он смог построить все другие виды правильных многогранников.

Если провести в противоположных гранях куба скрещивающиеся диагонали, то их концы окажутся вершинами тетраэдра, а вершины октаэдра – это центры граней куба. Полученные многоугольники действительно правильные, так как их грани – правильные треугольники. Равенство же двугранных углов следует из того, что при повороте куба ребро многогранника можно перевести в любое другое.

Для того, чтобы построить икосаэдр, на каждой грани куба нужно построить отрезок длиной x (пока что это – любая длина) так, чтобы он был параллелен двум сторонам своей грани и перпендикулярен таким же отрезкам на соседних гранях. Середина его должна совпадать с центром грани. Соединим концы этих отрезков между собой, и мы получим двадцатигранник, грани которого – треугольники, и при каждой вершине их пять.

Можно доказать, что отношение ребра куба к ребру вписанного в него икосаэдра – не что иное, как золотое сечение.

Теперь докажем равенство двугранных углов. Рассмотрим 5 ребер, выходящих из точки A. Концы их всех равноудалены и от точки A, и от центра куба O. Отсюда следует, что они лежат на пересечении двух сфер с центрами A и O, а значит – на окружности, причем ребра, соединяющие их с точкой A, равны. Значит, эти пять точек и точка a – вершины правильной пирамиды, а ее двугранные углы при вершине равны.

Додекаэдр из икосаэдра можно получить так же, как и октаэдр из куба. соединяя середины смежных граней икосаэдра, мы получаем правильнгый пятиугольни. Всего таких пятиугольников будет 12. Двугранные углы многоугольника будут равны, так как трехгранные углы при его вершинах имеют равные плоские углы.

Тела Платона - это выпуклые многогранники , все грани которых правильные многоугольники.

Существует всего пять правильных многогранников:

2.1. История названия правильных многогранников.

Итак, тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань.

Гексаэдр (куб) имеет 6 граней, "гекса" – шесть.

Октаэдр - восьмигранник, "окто" – восемь.

Додекаэдр - двенадцатигранник, "додека" - двенадцать;

Икосаэдр имеет 20 граней, "икоси" - двадцать.

2.2 Почему их только пять?

Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое. Рассмотрим развертку вершины такого многогранника. Каждая вершина может принадлежать трем и более граням.

Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360°.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.

Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.

3. Полуправильные многогранники

3.1. Тела Архимеда .

Многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники.

3.2 Тела Кеплера-Пуансо.

Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

3.3. Тела Федорова.

Федоров Евграф Степанович (22.12.1853 –

21.05.1919) - русский кристаллограф, один из

основоположников структурной кристаллографии и

минерологи, геометр, петрограф и геолог, стал

основоположником теории строения кристаллов. Его тела это выпуклые многогранники (параллелоэдры), параллельными переносами которых можно заполнить пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой (т.е. являются параллелоэдрами). Существует 5 типов Федоровых тел, найденных им в 1881г.

3.4. Каталановы тела

4. Биография Платона.

(428 или 427до н. э., —347 до н. э.,) —

Платон родился в семье, имевшей аристократическое происхождение. Первым учителем Платона был Кратил. Около 407 года познакомился с Сократом и стал одним из его учеников.

После смерти Сократа в 399 до н.э. уехал в Мегару.

В 389 году отправился в Южную Италию и Сицилию, где общался с пифагорейцами.

В 387 году Платон возвращается в Афины, где сновывает собственную школу — Платоновскую Академию. По древним преданиям Платон умер в

день своего рождения в 347 году. По свидетельству

Олимпиодора, Платон был не только философом, но и олимпийским чемпионом. Дважды он выигрывал соревнования по панкратиону — смесь бокса и борьбы.

4.1 Деятельность в цитатах.

Космос. Об отношении идеи к вещам.

Политико-правовое учение Платона.

"Человек существо бескрылое, двуногое, с плоскими ногтями, восприимчивое к знанию, основанному на рассуждениях".

Правильные многогранники или тела Платона Платону принадлежит разработка некоторых важных методологических проблем математического познания: аксиоматическое построение математики, исследование отношений между математическими методами и диалектикой, анализ основных форм математического знания.

4.2. Философия Платона

ПРОНИКНОВЕНИЕ ПРАВИЛЬНЫХ И ПОЛУПРАВИЛЬНЫХ МНОГОГРАННИКОВ В ОКРУЖАЮЩИЙ МИР

2.Многогранники в искусстве

Надгробный памятник в кафедральном соборе Солсбери.

Наш мир исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к правильным многогранникам - удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.

При производстве алюминия пользуются алюминиево-калиевыми квасцами (K[Al(SO4)2]·12H2O), монокристалл которых имеет форму правильного октаэдра.

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра (см.рис.).

В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Последний правильный многогранник – икосаэдр передает форму кристаллов бора (B). В свое время бор использовался для создания полупроводников первого поколения.

Итак, благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

На микроскопическом уровне, додекаэдр и икосаэдр являются относительными параметрами ДНК, по которым построена вся жизнь. Можно увидеть также, что молекула ДНК представляет собой вращающийся куб. При повороте куба последовательно на 72 градуса по определённой модели, получается икосаэдр, который, в свою очередь, составляет пару додекаэдру. Таким образом, двойная нить спирали ДНК построена по принципу двухстороннего соответствия : за икосаэдром следует додекаэдр, затем опять икосаэдр, и так далее. Это вращение через куб создаёт молекулу ДНК.

Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на правильный двадцатигранник, или икосаэдр. Есть вирусы, размножающиеся в клетках животных (позвоночных и беспозвоночных), другие облюбова-ли растения, третьи (их называют бактериофагами или просто фагами) паразитируют в микробах, но икосаэдрическая форма вирусов сохраняется во всех трех типах вирусов.

Пчелы – удивительные создания. Если разрезать пчелиные соты плоскостью, то станет видна сеть равных друг другу правильных шестиугольников. Из правильных многоугольников с одинаковой площадью наименьший периметр именно у правильных шестиугольниковСтало быть, мудрые пчелы экономят воск (≈2% ) и время для постройки сот. На рисунке 1 изображена пчелиная ячейка в общем виде. На рисунке 2 можно увидеть, как соприкасаются ячейки в улье: их общая часть является ромбом.

4. Мифические существа - духи.

Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили 4 земные стихии мифическими существами – духами (приложение 5):

воздуха (октаэдр) – эльфы,
земли (куб) – гномы, тролли,
огня (тетраэдр) – саламандры, фениксы,
воды (икосаэдр) – русалки, водяные.
Духи земли - подземные человечки - гномы, или кобольды, помогали людям находить
подземные богатства;
Духи воды – златокудрые русалки, или ундины, с рыбьим хвостом вместо ног, пели

вечерами обворожительные песни;

Духи огня – пляшущие в огне человечки в виде ящериц – саламандры.

Светлые эльфы в средневековой демонологии духи воздуха , — красивые, маленькие человечки (ростом с дюйм) в шапочках из цветков, беззаботно кружились в своем вечном танце.

5. Планета Земля и многогранники.

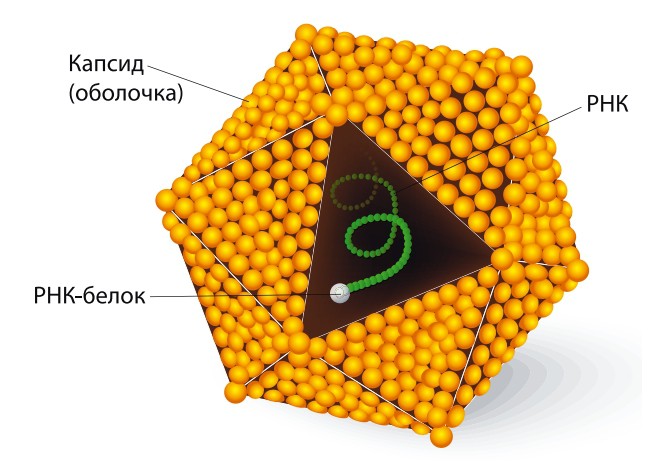
Вирус гепатита А, который вызывает болезнь Боткина, представляет собой правильный двадцатигранник — икосаэдр

Многогранники, как правильные, так и полуправильные, встречаются в природе: это и кристаллы, видимые невооруженным глазом, и вирусы, структуру которых можно различить только с помощью электронного микроскопа. Но что же такое многогранники? Мы знаем, что двумерная фигура — это множество отрезков, которые ограничивают часть плоскости, и называется она многоугольником. Отсюда понятно, что многогранник — это какое-то количество многоугольников, которые ограничивают часть трехмерного пространства. Многоугольники, которые образуют многогранник, называются его гранями.

С правильными многоугольниками все обстоит просто — их разнообразие бесконечно, хотя изобразить, например, миллионоугольник весьма проблематично. Но теоретически никаких ограничений на число сторон правильного многоугольника нет.

Вот какие существуют правильные многогранники.

Тетраэдр — пирамида, или четырехгранник, гранями которого являются четыре правильных треугольника и в каждой вершине сходятся три грани.
Октаэдр — восьмигранник, гранями которого являются восемь правильных треугольников и в каждой вершине сходятся четыре грани.
Куб, или гексаэдр, — шестигранник, гранями которого являются шесть квадратов и в каждой вершине сходятся три грани.
Додекаэдр — двенадцатигранник, гранями которого являются двенадцать правильных пятиугольников и в каждой вершине сходятся три грани.
Икосаэдр — двадцатигранник, гранями которого являются двадцать правильных треугольников и в каждой вершине сходятся пять граней.

Правильные многогранники называются Платоновыми телами. Дело в том, что Платон (428—348 гг. до н. э.) считал, будто каждой стихии соответствует определенное тело — правильный многогранник. Тетраэдр соответствует огню, октаэдр — воде, икосаэдр — воздуху. Куб, как самый устойчивый, соответствует земле. А додекаэдр — это пятый элемент, из которого состоят небесные тела. Платоновы тела напоминают собой атомы различных элементов в нашем понимании.

Памятник Платону в Афинах" />

Памятник Платону в Афинах. На фоне — статуя древнегреческой богини Афины, покровительницы знаний, искусств и ремесел

Архимедовы тела

Кроме правильных существуют также полуправильные многогранники. Архимед, как считается, описал некоторые из них. Архимедовы тела — это такие многогранники, у которых, в отличие от платановых тел, все грани — правильные многоугольники двух или более типов, а все многогранные углы при вершинах равны.

Читайте также: