Основные логические правила сообщение по математике
Обновлено: 02.07.2024
Элементы математической логики всё больше проникают в школьное образование: это и математика (логические истинности), и информатика (понятия и законы математической логики, умения строить таблицы истинности и логические схемы, умения строить и преобразовывать логические выражения). Элементы логики, стали “обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение”.
Особое место занимает понятие логически истинного предложения (логическая истина), оно является центральным логическим понятием, представляя логику в рассуждениях и доказательствах.
В статье я сделаю попытку показать, как можно ввести понятие “логическая истина” в жизнь обычного школьника.
Перед Вами изложение теоретического материала для учащихся (текст выдаётся каждому школьнику, который добровольно пришёл на математический семинар). Как правило, длительность семинара от 45 минут (1 занятие) до 225 (5 занятий). Темы и время проведения семинаров объявляются в начале учебного периода: четверти, полугодия. В семинаре участвуют, как минимум 6 учеников, как максимум 20, всё зависит от заявленной темы. Участники – ребята разных классов: в 2010/2011 – 9, 10, 11 классы, в 2011/2012 году – 6, 8 классы, в 2012/2013 – 7, 9.
Тема. Логические истины. (225 минут)
Очевидно, что каждая наука имеет свой словарь. Например, в биологическом словаре: анабиоз, бактериофаг, гаметы, ген, клетка, селекция, штамм; в музыкальном словаре: бард, двойной хор, запев, звукоряд, фальцет; в физическом словаре: масса, путь, скорость; в химическом – молекула, моль, реакция; в математическом – многоугольник, число, уравнение, функция.
Выясним, какие слова входят в словарь математической логики, а также что такое логическая истина. Рассмотрим известное предложение: “Если все люди смертны ()и все герои – люди (), то все герои смертны ()”. Ясно, что это предложение истинное. Заменим в этом предложении слова “люди”, “смертны” и “герои” соответственно словами “животные”, “дышат”, “киты”. Получим новое предложение: “Если все животные дышат и все киты – животные, то все киты дышат”, которое также истинное. Таких замен можно привести достаточно много. Приведённые предложения имеют различные сюжеты (содержание или смысл), однако, их истинность не нарушилась от замены содержания.
Очистим рассматриваемые предложения от их содержания, и получим форму:
“Если все *1, *2 и все *3 есть *1 все *3 *2” Подставив в полученную форму одни и те же слова вместо одинаково пронумерованных звёздочек, всегда получим истинные предложения. Итак, предложения, истинность которых зависит только от формы и не зависит от содержания, называются логически истинными предложениями (логическими истинами).
- Я сдам или не сдам зачёт по математике.
- Из того, что если я отдыхаю, то я сплю, следует, что если я не сплю, то я не отдыхаю.
- Электрическое напряжение в сети есть или его нет.
- Если существует х такое, что 5 – х = 0, то не для всех х не имеет места 5 – х = 0.
Слова, из которых строится форма предложения, составляют логический словарь.
Это – “и”, “или”, “не”, “если…, то…”, “тогда и только тогда”, “все”, “существует”, “некоторые”, “никакой” и т.д.
Изучение логических истин – основная задача логики, вернее одна из основных задач. Однако, критерий истинности в логике не такой, как в естественных науках. В естественных науках важна не форма, а содержание. Подтверждение истинности в естественных науках требует проведение эксперимента, наблюдений. В логике критерий истинности во многом определяется синтаксической структурой (формой) предложения.
При аксиоматическом построении математики (в частности геометрии) теорему мы рассматриваем как некое условное предложение, логическую истинность которого доказываем.
Рассмотрим основные понятия и символику математической логики.
По аналогии – двуместный предикат с областью значений (х; у) где и х и у – действительные числа. (1; -6) превращает предикат в истинное высказывание, (1; 6) – ложное.
В логике принято однозначно определять истинность сложного высказывания через истинность высказываний его составляющих, пользуясь следующими договоренностями.
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание. Суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита. Истинному высказыванию соответствует значение логической переменной 1, а ложному – 0.
Несколько советов учителю, которому интересна идея введения элементов логики в школе (элективный курс, семинар для желающих учеников, . ).
По моему мнению, логическая подготовка школьников может быть разделена на три этапа.
1. Подготовительный этап
Необходимо учить школьников (начинать можно уже в начальной школе) понимать логическую структуру предложений и правильно применять слова и словосочетания, такие как: “и”, “или”, “не”, “хотя бы…”, “если…, то…”, “необходимо”, “достаточно”, “необходимо и достаточно”, “все”, “некоторые” и др. Постепенно приучать находить истинность или ложность сложных предложений в зависимости от их логического строения и истинностных значений, составляющих их предложений. Ученик должен твёрдо усвоить, что запись – истинное высказывание, потому что это сложное высказывание “ или 2 > 2“, которое истинно, если…
Особое внимание необходимо уделить выработке навыка правильного понимания условных предложений. Он должен без колебаний относить предложения “Если , то 1 = 1”, “Если 0 = 1, то 1 = 2” к истинным высказываниям. Думаю, что в разумных пределах, необходимо учить школьников пользоваться логической символикой.
2. Формирование понятия о логическом законе
Идею логического закона следует формировать постепенно, не стремясь к формальным и строгим определениям. Необходимо в начале научить выделять логические истины, делая акцент на их отличии от не логических, фактических истин, учить замечать общую форму логических истин, прибегая к символике, доказывать простые логические законы и опровергать ошибочные гипотезы о логической истинности предложений.
3. Выработка навыков использования логических законов в рассуждениях.
Без четкого понимания логических связей, логических законов, отношений следования и эквивалентности ученики способны лишь заучить доказательство, оказываются беспомощными в попытках самостоятельно его отыскать.
Одна из центральных задач обучения математике состоит в обучении установлению истинности математических предложений (чаще всего с помощью доказательства), а истинностные значения этих предложений зависят от их логической структуры, то естественно считать одной из главных задач обучения математике раскрытие логической структуры математических предложений.
Каждая математическая теория представляет собой множество предложений, описывающее какую-то структуру (если эта теория излагается содержательно в определенной конкретной интерпретации, как это имеет место в школьном обучении).
- предложение записано (или сформулировано) на языке данной теории, состоит из математических (принадлежащих языку теории) и логических терминов или символов и не содержит никаких других терминов или символов;
- предложение истинно, т. е. является или исходным истинным предложением (аксиомой) данной теории, или его истинность устанавливается доказательством с помощью уже известных (исходных или ранее доказанных) истинных предложений.
Например, предложение “Вертикальные углы равны” является геометрическим предложением, принадлежит теории евклидовой геометрии, потому что: оно записано на языке геометрии (и одновременно па русском языке), т. е. состоит из геометрических (“вертикальные углы”) и логических (“равны”) терминов или символов; оно истинно, так как доказывается в рамках евклидовой геометрии, т. е. на основе ее аксиом или других уже доказанных предложений этой теории.
С каждым математическим предложением связаны содержание (выраженное в нем математическое содержание) и логическая форма (или структура).
Представление, что можно ограничиться в обучении математике лишь раскрытием содержания каждого математического предложения, ошибочно. Содержание неразрывно связано с формой, и нельзя осмыслить первое без понимания второй.
Раскрыть логическую структуру сложного (составного) предложения – значит показать, из каких элементарных предложений сконструировано данное сложное предложение и как оно составлено из них, т. е. с помощью каких и в каком порядке применяемых логических связок (слов или сочетаний слов) “не”, “и”, “или” , “если. то” , “тогда и только тогда” , “для всякого” , “существует” (и некоторых синонимических выражений), обозначающих логические операции, с помощью которых из одних предложений образуются другие.
Всякое математическое (и не только математическое) предложение либо элементарное, (не расчленяется на части, каждая из которых в свою очередь есть предложение), либо построено из элементарных, определенным образом соединенных между собой логическими связками.
Логическую структуру любого сложного предложения необходимо раскрывать с обязательным разъяснением точного смысла применяемых логических связок.
Такое разъяснение необходимо потому, что, применение, даже многократное, перечисленных выше слов само по себе еще не обеспечивает правильного понимания их смысла. Не только школьники, но и некоторые взрослые, много тысяч раз применявшие в своих рассуждениях союз “или”, отвечают отрицательно, например, на вопрос: «Истинно ли предложение ’’4 13.07.2013
Эта лицензия позволяет другим редактировать, поправлять и брать за основу ваше произведение в некоммерческих целях до тех пор пока они указывают вас в качестве автора и лицензируют их новые творения на идентичных условиях.
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
6) Операция XOR (исключающие или)
Обозначение: F = A ⊕ B .
| A | B | F |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…).
В общем случае таблицы истинности имеют размер 2 N строк комбинаций для N независимых логических переменных.
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
A → B = ¬ A \/ B
Для замены операции эквивалентности существует два правила:
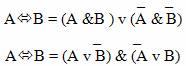
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Определение взаимодействия законов логики и правил алгебры. Основные понятия и термины двух наук – логики и алгебры. Примеры логических и алгебраических выражений. Математический анализ и математическая логика выдающегося ученого Огастесе де Моргана.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 23.12.2017 |
| Размер файла | 291,1 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Законы логики и правила алгебры: сходства и различия
Введение
логика алгебра морган
В данном реферате я хотела бы рассмотреть такие науки как логику и алгебру, их законы и правила, сходства и различия.
Логика - одна из древнейших наук. Еще древнегреческий философ Аристотель систематизировал формы и правила мышления, разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы формальной логики.
1. Логика
Логика - наука о законах и формах мышления
Высказывание (суждение) - некоторое предложение, которое может быть истинно (верно) или ложно
Утверждение - суждение, которое требуется доказать или опровергнуть
Рассуждение - цепочка высказываний или утверждений, определенным образом связанных друг с другом
Умозаключение - логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение
Логическое выражение - это запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0). Сложное логическое выражение - логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
1.1 Законы логики
Законы логики отражают наиболее важные закономерности логического мышления.
Всякое высказывание тождественно самому себе.
Высказывание не может быть одновременно истинным и ложным. Если высказывание А истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
Закон исключенного третьего
Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.
Законы де Моргана
Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в алгебре.
В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения.
Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять.
(А & B) & С = А & (В & С)
(А \/ В) \/ С= А \/ (В \/ С)
В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые.
ШA & (A \/ B) = ШA & B
1.2 Логические выражения
Если логическое выражение содержит большое количество операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести в нормальную форму.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при логических переменных.Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
В качестве основных логических операций в сложных логических выражениях используются следующие:
* НЕ (логическое отрицание, инверсия);
* ИЛИ (логическое сложение, дизъюнкция);
* И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение -- двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
2. Алгебра
Данный раздел математики традиционно включает следующие категории:
Элементарная алгебра, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгебра содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием алгебра.
Общая алгебра, иногда называемая современной алгеброй или абстрактной алгеброй, где аксиоматизируются и изучаются максимально общие алгебраические структуры, такие, как группы, кольца и поля.
Универсальная алгебра, в которой изучаются свойства, общие для всех алгебраических структур (считается подразделом общей алгебры). Линейная алгебра, в которой изучаются свойства векторных пространств.
Алгебраическая комбинаторика, в которой методы абстрактной алгебры используются для изучения вопросов комбинаторики.
В алгебре принято записывать математические выражения (формулы) в самом общем виде, заменяя конкретные числа на буквенные символы, благодаря чему при решении однотипных задач достигается максимальная общность результата. Основным содержанием алгебры являются правила тождественных преобразований формул, необходимые для решения уравнений, анализа зависимостей, оптимизации изучаемой системы и других практических задач. Кроме букв и чисел, в формулах элементарной алгебры используются арифметические операции: (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня) и элементарные функции (логарифм, тригонометрические функции). Две формулы, соединённые знаком равенства, называются уравнением.
2.1 Законы элементарной алгебры
Порядок выполнения операций указывается скобками. Если скобок нет, то приоритетность, в порядке убывания, следующая:
- Возведение в степень.
- Умножение и деление.
- Сложение и вычитание.
Независимо от природы рассматриваемых чисел и от определения суммы и произведения чисел общие законы действия над числами остаются одни и те же.
2.2 Свойства операций
Коммутативность (перестановочное свойство) сложения:
Ассоциативное (сочетательное) свойство сложения:
Ассоциативное (сочетательное) свойство умножения:
Коммутативное (переместительное) свойство сложения:
Коммутативное (переместительное) свойство умножения:
Дистрибутивное (распределительное) свойство для умножения:
(а + b + c) · d = аd + bd + cd
3. Сходства и различия между законами логики и правилами алгебры
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Логика как наука позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления являются понятия, суждения и умозаключения. В то время как предметом изучения современной алгебры являются множества с заданными на них алгебраическими операциями. При этом если между такими множествами можно установить изоморфизм (взаимно-однозначное соответствие, сохраняющее операции), то множества считаются одинаковыми, и поэтому природа множеств безразлична.
4. Огастес де Морган
Морган Огастес (Августус) де (27.6.1806-18.3. 1871) - шотландский математик и логик. Секретарь Королевcкого астрономического общества (1847г.), член Лондонского королевского общества. Первый президент Лондонского математического общества. Родился в Мадуре (Индия). Учился в Тринити-колледж (в Кембридже). Профессор математики в университетском колледже в Лондоне. В теории рядов описал логарифмическую шкалу для критериев сходимости; занимался теорией расходящихся рядов. Один из основателей формальной алгебры. Продолжая работы Дж. Пикока, Морган в 1841-1847 гг. опубликовал ряд работ по основам алгебры. В трактате "Формальная логика или исчисление выводов необходимых и возможных" (1847г.), Морган некоторыми своими положениями опередил Дж. Буля. Позднее Морган успешно изучал логику отношений - область, не охваченную исследованиями предшественников. Написал много исторических работ, в частности книгу "Бюджет парадоксов" (1872г.). Большой вклад внес также в дедуктивную логику вообще и математическую в частности. Лондонское математическое общество учредило медаль им. О. Моргана.
Таким образом, в данном реферате я рассмотрела основные понятия логики и алгебры, их законы и взаимодействие.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Наряду с этим объектом изучения алгебры являются сами алгебраические операции, а законы логики отражают наиболее важные закономерности логического мышления.
Приложение
Подобные документы
Основные аксиомы и тождества алгебры логики. Аналитическая форма представления булевых функций. Элементарные функции алгебры логики. Функции алгебры логики одного аргумента и формы ее реализации. Свойства, особенности и виды логических операций.
реферат [63,3 K], добавлен 06.12.2010
Основные понятия алгебры логики. Дизъюнктивные и конъюнктивные нормальные формы. Сущность теоремы Шеннона. Булевы функции двух переменных. Последовательное и параллельное соединение двух выключателей. Свойства элементарных функций алгебры логики.
контрольная работа [345,3 K], добавлен 29.11.2010
Основы формальной логики Аристотеля. Понятия инверсии, конъюнкции и дизъюнкции. Основные законы алгебры логики. Основные законы, позволяющие производить тождественные преобразования логических выражений. Равносильные преобразования логических формул.
презентация [67,8 K], добавлен 23.12.2012
Понятие алгебры логики, ее сущность и особенности, основные понятия и определения, предмет и методика изучения. Законы алгебры логики и следствия из них, методы построения формул по заданной таблице истинности. Формы представления булевых функций.
учебное пособие [702,6 K], добавлен 29.04.2009
Операции над логическими высказываниями: булевы функции и выражение одних таких зависимостей через другие. Пропозициональные формулы и некоторые законы логики высказываний. Перевод выражений естественного языка на символическую речь алгебры логики.
Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.
При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.
Законы алгебры высказываний (алгебры логики) — это тавтологии.
Иногда эти законы называются теоремами.
В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.
Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.
Закон тождества:
Всякое понятие и суждение тождественно самому себе.
Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.
Закон непротиворечия :
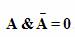
В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:
1. Число 12345 либо четное, либо нечетное, третьего не дано.
2. Предприятие работает убыточно или безубыточно.
3. Эта жидкость является или не является кислотой.
Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.
Например, определим, чему эквивалентно (равносильно) А (двойное отрицание А , т. е. отрицание отрицания А ).Для этого построим таблицу истинности:
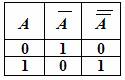
По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.
Таким образом, мы можем сформулировать закон двойного отрицания:
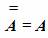
Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. Например, высказывание А = Матроскин — кот эквивалентно высказыванию А = Неверно, что Матроскин не кот .
Аналогичным образом можно вывести и проверить следующие законы:
Свойства констант:
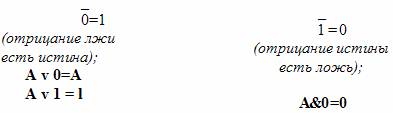
Законы идемпотентности:
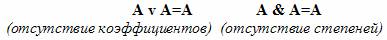
Сколько бы раз мы ни повторяли: телевизор включен или телевизор включен или телевизор включен . значение высказывания не изменится. Аналогично от повторения на улице тепло, на улице тепло. ни на один градус теплее не станет.
Законы коммутативности:
Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.
Законы ассоциативности:
A v(B v C) = (A v B) v C;
А & (В & C) = (A & В) & С.
Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.
Законы дистрибутивности:
A v (B & C) = (A v B) &(A v C)
(дистрибутивность дизъюнкции
относительно конъюнкции)
А & (B v C) = (A & B) v (А & C)
(дистрибутивность конъюнкции
относительно дизъюнкции)
Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:
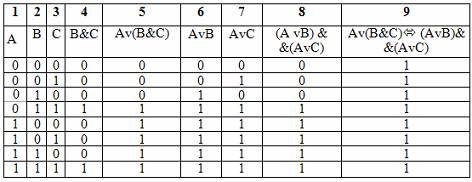
Законы поглощения:
Проведите доказательство законов поглощения самостоятельно.
Законы де Моргана:
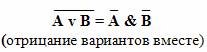
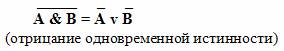
Словесные формулировки законов де Моргана:


Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.
Примеры выполнения закона де Моргана:
1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.
2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
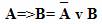
Для замены операции эквивалентности существует два правила:
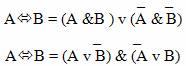
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.
Читайте также:

