Формула схема бернулли сообщение
Обновлено: 02.07.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Я выбралаэту тему потому что, на схемах Бернулли установление важные закономерностей теории вероятностей как математической науки, относящихся к сумме независимых случайных величин и представляющих закон больших чисел. Под законом больших чисел в теории вероятностей принято понимать ряд математических теорем, устанавливающих факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Важные теоремы, составляющие закон больших чисел, впервые были выведены для схемы испытаний Бернулли.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А, причем нас не интересует результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.
Определение. Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания.
Например, несколько бросаний монеты представляют собой независимые испытания.
Пусть произведено два испытания(n=2). В результате возможно наступление одного из следующих событий:
Соответствующие вероятности данных событий такие:
или — наступление события только в одном испытании.
— вероятность наступления события два раза.
— вероятность наступления события только один раз.
— вероятность наступления события нуль раз.
Пусть теперь n=3. Тогда возможно наступление одного из следующих вариантов событий:
Соответствующие вероятности равны.
Очевидно, что полученные результаты при n=2 и n=3 являются элементами .
Теперь допустим, произведено n испытаний. Событие А может наступить n раз, 0 раз, n-1 раз и т.д. Напишем событие, состоящее в наступлении события А m раз
Необходимо найти число испытаний, в которых событие А наступит m раз. Для этого надо найти число комбинаций из n элементов, в которых А повторяется m раз, а n-m раз.
— вероятность наступления события А.
Последняя формула называется формулой Бернулли и представляет собой общий член разложения :
Из формулы (1) видно, что ее удобно использовать, когда число испытаний не слишком велико.
№ 1. Бросается монета 7 раз. Найти вероятность наступления орла три раза.
Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами. Естественно, возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли.
В 1730 г. другой метод решения при p=1/2 нашел Муавр; в 1783 г. Лаплас обобщил формулу Муавра для произвольного p, отличного от 0 и 1.
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события не слишком близка к нулю или единице. Поэтому теорему, о которой идет речь, называют теоремой Муавра-Лапласа.
Теорема Муавра-Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях ровно k раз, приближенно равна(тем точнее, чем больше n) значению функции
Имеются таблицы, в которых помещены значения функции
соответствующие положительным значениям аргумента x(см. приложение1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция четна, т.е. .
Итак, вероятность того, что событие A появится в n независимых испытаниях ровно k раз, приближенно равна
№ 14. Вероятность поражения мишени стрелком при одном выстреле p=0,75.
Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение. По условию n=10; k=8; p=0,75; q=0,25.
Воспользуемся формулой Лапласа:
Вычислим определяемое данными задачи значение x:
По таблице приложения1 находим
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события достаточно близка к 0 или 1.
Таким образом получили формулу:
№ 17. Вероятность изготовления негодной детали равна 0,0002. Найти вероятность того, что среди 10000 деталей только 2 детали будут негодными.
Решение. n=10000; k=2; p=0,0002.
№ 18. Вероятность изготовления бракованной детали равна 0,0004. Найти вероятность того, что среди 1000 деталей только 5 детали будут бракованными.
Решение. n=1000; k=5; p=0,0004.
Теорема . Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна удвоенной функции Лапласа при :
Доказательство. Будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства
Заменим неравенство (*) ему равносильными:
Умножая эти неравенства на положительный множитель , получим неравенства, равносильные исходному:
Тогда вероятность найдем следующим образом:
Значение функции находится по таблице(см. приложение2).
№ 20. Вероятность того, что деталь не стандартна, p=0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,1 по абсолютной величине не более, чем на 0,03.
Решение. n=400; p=0,1; q=0,9; =0,03. Требуется найти вероятность . Пользуясь формулой
По таблице приложения2 находим . Следовательно, . Итак, искомая вероятность равна 0,9544.
№ 21. Вероятность того, что деталь не стандартна, p=0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей(среди отобранных) отклонится от постоянной вероятности p по абсолютной величине не более чем на 0,03.
Решение. По условию, p=0,1; q=0,9; =0,03; . Требуется найти n. Воспользуемся формулой
По таблице приложения 2 находим . Для отыскания числа n получаем уравнение . Отсюда искомое число деталей n=400.
№ 22. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.
Определение повторных независимых испытаний. Формулы Бернулли для вычисления вероятности и наивероятнейшего числа. Асимптотические формулы для формулы Бернулли (локальная и интегральная, теоремы Лапласа). Использование интегральной теоремы. Формула Пуассона, для маловероятных случайных событий.
Повторные независимые испытания
На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие появлений события испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события повторными независимыми.
Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом.
Формула Бернулли
Воспользуемся понятием сложного события , под которым подразумевается совмещение нескольких элементарных событий, состоящих в появлении или непоявлении события –м испытании. Пусть проводится независимых испытаний, в каждом из которых событие , либо не появиться с вероятностью . Рассмотрим событие , состоящее в том, что событие испытаниях наступит ровно раз и, следовательно, не наступит ровно раз. Обозначим появление события — непоявление события –м испытании. В силу постоянства условий испытания имеем
Событие раз в разных последовательностях или комбинациях, чередуясь с противоположным событием . Число возможных комбинаций такого рода равно числу сочетаний из элементов по , т. е. . Следовательно, событие можно представить в виде суммы сложных несовместных между собой событий, причем число слагаемых равно :
где в каждое произведение событие раз, а — раз.
Вероятность каждого сложного события, входящего в формулу (3.1), по теореме умножения вероятностей для независимых событий равна . Так как общее количество таких событий равно , то, используя теорему сложения вероятностей для несовместных событий, получаем вероятность события (обозначим ее )
Формулу (3.2) называют формулой Бернулли , а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события испытаниями Бернулли , или схемой Бернулли .
Пример 1. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0,07. Определить вероятность того, что из пяти наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску.
Решение. Условие задачи удовлетворяет требования схемы Бернулли. Поэтому, полагая , по формуле (3.2) получаем
Пример 2. Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?
Наивероятнейшее число появлений события
Наивероятнейшим числом появления события независимых испытаниях называется такое число , для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события и вероятность появления события вероятность, соответствующую наивероятнейшему числу . Используя формулу (3.2), записываем
Согласно определению наивероятнейшего числа, вероятности наступления события и раз должны, по крайней мере, не превышать вероятность , т. е.
Подставляя в неравенства значение и выражения вероятностей и , получаем
Решая эти неравенства относительно , получаем
Объединяя последние неравенства, получаем двойное неравенство, которое используют для определения наивероятнейшего числа:
Так как длина интервала, определяемого неравенством (3.4), равна единице, т. е.
и событие может произойти в испытаниях только целое число раз, то следует иметь в виду, что:
1) если — целое число, то существуют два значения наивероятнейшего числа, а именно: и ;
2) если — дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства (3.4);
3) если — целое число, то существует одно наивероятнейшее число, а именно: .
При больших значениях пользоваться формулой (3.3) для расчета вероятности, соответствующей наивероятнейшему числу, неудобно. Если в равенство (3.3) подставить формулу Стирлинга
справедливую для достаточно больших , и принять наивероятнейшее число , то получим формулу для приближенного вычисления вероятности, соответствующей наивероятнейшему числу:
Пример 2. Известно, что часть продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу была завезена партия изделий в количестве 250 шт. Найти наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, и вычислить вероятность того, что в этой партии окажется наивероятнейшее число изделий.
Решение. По условию . Согласно неравенству (3.4) имеем
откуда . Следовательно, наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, в партии из 250 шт. равно 234. Подставляя данные в формулу (3.5), вычисляем вероятность наличия в партии наивероятнейшего числа изделий:
Локальная теорема Лапласа
Пользоваться формулой Бернулли при больших значениях очень трудно. Например, если , то для отыскания вероятности надо вычислить значение выражения
Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно раз в испытаниях, если число испытаний достаточно велико.
Теорема 3.1. Если вероятность появления события того, что событие испытаниях ровно раз, приближенно равна (тем точнее, чем больше ) значению функции
Существуют таблицы, которые содержат значения функции , соответствующие положительным значениям аргумента четна, т. е. .
Итак, приближенно вероятность того, что событие испытаниях ровно раз,
Пример 3. Найти вероятность того, что событие Решение. По условию . Воспользуемся асимптотической, формулой Лапласа:
Вычислим определяемое данными задачи значение
По таблице прил, 1 находим . Искомая вероятность
Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):
Интегральная теорема Лапласа
Предположим, что проводится независимых испытаний, в каждом из которых вероятность появления события . Необходимо вычислить вероятность того, что событие испытаниях не менее и не более раз (для краткости будем говорить "от до раз"). Это можно сделать с помощью интегральной теоремы Лапласа.
Теорема 3.2. Если вероятность наступления события того, что событие до раз,
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл не выражается через элементарные функции. Таблица для интеграла приведена в прил. 2, где даны значения функции для положительных значений используют ту же таблицу (функция нечетна, т. е. ). Таблица содержит значения функции лишь для ; для можно принять .
Итак, приближенно вероятность того, что событие независимых испытаниях от до раз,
Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, . Найти вероятность того, что среди 400 случайно отобранных деталей нестандартных окажется от 70 до 100 деталей.
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
- бросание монеты или игрального кубика (вероятности выпадения герба/решки или определенной цифры одинаковы в каждом броске);
- извлечение из урны шара при условии, что вынутый шар после записи его цвета кладется обратно в урну (то есть состав шаров в урне не меняется и не меняется вероятность вынуть шар нужного цвета);
- включение приборов (ламп, станков и т.п.) с заранее заданной одинаковой вероятностью выхода из строя каждого;
- повторение стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой и т.д.
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем $n$ испытаний Бернулли. Это означает, что все $n$ испытаний независимы; вероятность появления события $А$ в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события $А$ в единичном испытании буквой $р$, т.е. $p=P(A)$, а вероятность противоположного события (событие $А$ не наступило) - буквой $q=P(\overline)=1-p$.
Тогда вероятность того, что событие $А$ появится в этих $n$ испытаниях ровно $k$ раз, выражается формулой Бернулли
$$P_n(k)=C_n^k \cdot p^k \cdot q^, \quad q=1-p.$$
Распределение числа успехов (появлений события) носит название биномиального распределения.
Онлайн-калькуляторы для формулы Бернулли
Некоторые наиболее популярные типы задач, в которых используется формула Бернулли, разобраны в статьях и снабжены онлайн-калькулятором, вы можете перейти к ним по ссылкам:
Примеры задач с решениями
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности
, .
По формуле Бернулли требуемая вероятность равна
.
Пример. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки
, тогда .
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
Следовательно, искомая вероятность
Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них .
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
Надо заметить, что использование биномиального закона при большом числе испытаний вычислительно трудно. Поэтому с возрастанием значений $n$ становится целесообразным применение приближенных формул (Пуассона, Муавра-Лапласа), которые будут рассмотрены в следующих разделах.
Видеоурок про формулу Бернулли
Для тех, кому нагляднее последовательное видеообъяснение, 15-минутный ролик:

Кто такой Бернулли?
Д. Бернулли (1700-1782)
Идеальная жидкость и течение идеальной жидкости
Помимо известной нам материальной точки и идеального газа существует также идеальная жидкость. Какой-нибудь студент, конечно, может подумать, что эта жидкость – его любимое пиво или кофе, без которого невозможно жить. Но нет, идеальная жидкость – это жидкость, которая абсолютно несжимаема, лишена вязкости и теплопроводности. Тем не менее, такая идеализация дает вполне хорошее описание движения реальных жидкостей в гидродинамике.
Течением жидкости называется движение ее слоев относительно друг друга или относительно всей жидкости.
Помимо того есть разные режимы течения жидкости. Нас интересует тот случай, когда скорость потока в какой-то конкретной точке не меняется со временем. Такой поток называют стационарным. При этом скорость течения в различных точках стационарного потока может различаться.
Поток жидкости– совокупность частиц движущейся жидкости.

Вывод уравнения Бернулли
Но как описать движение жидкости? Для этого нам нужно знать вектор скорости частиц, точнее зависимость его от времени. Совокупность скоростей в разных точках потока дает поле вектора скорости.
Рассмотрим стационарное течение жидкости по трубке. В одном месте сечение этой трубки равно S1, а в другой – S2. При стационарном потоке через оба сечения за одинаковый промежуток времени пройдет одинаковое количество жидкости.

Данное уравнение – уравнение неразрывности струи.
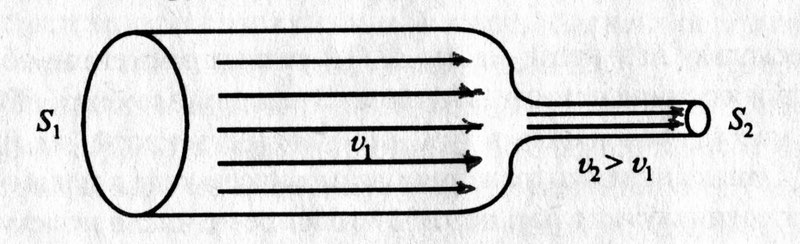
К выводу уравнения Бернулли
Узнав его, Бернулли решил установить связь между давлением и скоростью жидкости в разных сечениях. Полное давление – это сумма статистического (обусловлено потенциальной энергией жидкости) и динамического давлений (обусловлено кинетической энергией). Оказывается, сумма статического и динамического давлений в любом сечении трубы постоянна. Само же уравнение Бернулли имеет вид:

Смысл уравнения Бернулли
Физический смысл уравнения Бернулли. Уравнение Бернулли является следствием закона сохранения энергии. Первый член уравнения Бернулли – это кинетическая энергия, второе слагаемое уравнения Бернулли – потенциальная энергия в поле силы тяжести, третье – работа силы давления при подъеме жидкости на высоту h.
Вот и все, друзья, не так уж и страшно. Совсем немного времени, а Вы уже знаете уравнение Бернулли. Даже если Вы не знаете больше ничего, с этими знаниями идти на экзамен или зачет гораздо лучше, чем просто так. А если Вам необходима помощь в том, как решать задачи на уравнение Бернулли – не стесняйтесь и оформляйте заявку. После того как наши авторы распишут решение уравнения Бернулли максимально подробно, у Вас не останется пробелов в знаниях.
Читайте также:

