Частицы в одномерной прямоугольной яме сообщение

Обновлено: 02.07.2024

Изучение движения свободной частицы. Частица в одномерной прямоугольной яме с бесконечными внешними стенками. Гармонический осциллятор. Прохождение частиц сквозь потенциальный барьер. Туннельный эффект. Качественный анализ решений уравнения Шредингера.

Рубрика	Физика и энергетика
Вид	презентация
Язык	русский
Дата добавления	07.03.2016
Размер файла	376,0 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

HTML-версии работы пока нет.
Cкачать архив работы можно перейдя по ссылке, которая находятся ниже.

Подобные документы

Соотношения неопределенностей Гейзенберга. Формулировка уравнения Шредингера. Частица в потенциальной яме. Ее прохождение через потенциальный барьер. Основные свойства, излучение и поглощение атома водорода. Движение электронов по заданным орбитам.

реферат [1,8 M], добавлен 21.03.2014

Исследование особенностей движения заряженной частицы в однородном магнитном поле. Установление функциональной зависимости радиуса траектории от свойств частицы и поля. Определение угловой скорости движения заряженной частицы по круговой траектории.

лабораторная работа [1,5 M], добавлен 26.10.2014

Прямоугольный потенциальный барьер. Туннельный эффект как квантовый переход системы через область движения, запрещённую классической механикой. Кажущаяся парадоксальность данного эффекта. Вырывание электронов из металла. Контактная разность потенциалов.

курсовая работа [3,2 M], добавлен 26.02.2010

Элементарная частица — частица без внутренней структуры, то есть не содержащая других частиц. Классификация элементарных частиц, их символы и масса. Цветовой заряд и принцип Паули. Фермионы как базовые составляющие частицы всей материи, их виды.

презентация [214,8 K], добавлен 27.05.2012

курсовая работа [3,3 M], добавлен 27.08.2012

Движение несвободной частицы. Силы реакции и динамика частиц. Движение центра масс, закон сохранения импульса системы. Закон сохранения кинетического момента системы. Закон сохранения и превращения механической энергии системы частиц. Теорема Кёнига.

доклад [32,7 K], добавлен 30.04.2009

Определение начальной энергии частицы фосфора, длины стороны квадратной пластины, заряда пластины и энергии электрического поля конденсатора. Построение зависимости координаты частицы от ее положения, энергии частицы от времени полета в конденсаторе.

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:

Т.е. стационарное уравнение Шредингера, описывающее движение частицы в потенциальной яме с бесконечно высокими стенками, удовлетворяется только при собственных значениях En, зависящих от целого числа n. Следовательно, энергия En частицы в потенциальной яме с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии En называются уровнями энергии, а число п, определяющее энергетические уровни – главным квантовым числом.

Стационарным состоянием (от лат. stationarius — стоящий на месте, неподвижный) называется состояние квантовой системы, при котором её энергия и другие динамические величины, характеризующие квантовое состояние, не изменяются. Существование таких состояний для атома было предсказано А. Эйнштейном в 1906 г. и подтверждено Н. Бором в 1916 г. На основе полученных данных, Бор сформулировал свои постулаты. Согласно его выводам, атом может переходить из одного стационарного состояния в другое лишь с помощью поглощения или выделения кванта с энергией, равной разности энергий атома в начальном и конечном стационарных состояниях. если система замкнутая и оператор полной энергии не зависит от времени, то для такой системы существуют стационарные состояния с точно определенной энергией, в которых все измеряемые величины не меняются во времени. Стационарные состояния описываются собственными функциями оператора полной энергии

и Е – собственное значение оператора полной энергии или энергия стационарного состояния. Уравнение (II.3.14a) получается путем подстановки функции (II.3.14б) в уравнение (II.3.11) и называется стационарным уравнением Шредингера.

Туннельным эффектом называется прохождение микрочастицы сквозь потенциальный барьер. Потенциальный барьер – увеличение потенциальной энергии в некоторой области пространства.

Рассмотрим такой мысленный эксперимент, который, впрочем, каждый легко может проделать реально. Возьмем мяч и бросим его в стенку. Мяч не пробьет стенку, а отскочит назад. Почему? Его энергия мала для пробивания стены. Если вместо мяча пробивать стену снарядом, то результат эксперимента будет положительный (снаряд пробьет стену), так как у снаряда достаточно энергии. Этот эксперимент - наглядная иллюстрация ситуации, изображенной на рис. 12. Для мяча полная энергия Е меньше высоты барьера, для снаряда – больше. Таким образом, в классической механике туннельный эффект невозможен. Для квантовомеханической частицы возможно прохождение “сквозь” барьер, даже если высота этого барьера больше её полной энергии. Частица как бы проходит сквозь открывшийся для нее “туннель” в стене, откуда и название эффекта. Таким образом, туннельный эффект – явление чисто квантовомеханическое и объясняется законами квантовой механики.

Для объяснения туннельного эффекта рассмотрим частицу, находящуюся в потенциальном ящике со стенками конечной высоты Такой ящик изображен на рис. 13. Частица находится в области координат x1 x2:

Таким образом, имеется конечная, отличная от нуля вероятность нахождения частицы в области координат x > x2, т.е. за пределами ящика, хотя её энергия и меньше высоты стенок.

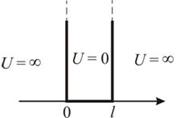
Пространственно ограниченное квантовое движение- одномерное движение чатицы, находящейся в силовом поле, энергия взаимодействия с которым имеет вид бесконечно глубокой потенциальной ямы с вертикальными стенками. Находясь внутри ямы, частица движется свободно на участке , а на краях силовое поле возвращает ее обратно в яму.

Потенциальная яма , где - ширина ямы, а энергия отсчитывается от ее дна. Никакая частица не может выйти из этой ямы. Если частица классическая, то на участке она движется с неизменным импульсом и энергией. Достигая стенок ямы, частица испытывает упругий удар и меняет направление на противоположное. Частота таких колебаний частицы зависит от скорости частицы и ширины ямы . В зависимости от скорости, если

1) , то положим равной 0; 2) : частица движется между стенками, и график плотности распределения вероятности будет выглядеть в виде прямой (см. рисунок).

Для реальной частицы: запишем уравнение Шредингера, учитывая что внутри ямы U=0: . За пределы ямы частица не проникает, поэтому волновая функция вне ямы равна 0, следовательно, на границах ямы . С учетом граничных условий волновая функция должна представлять собой стоячую волну. Решение ищем в виде . . . По второму граничному условию: . , где n - квантовое число. Для определения constC используем условие нормировки: , т. к. вероятность обнаружения частицы внутри ямы равна 1, следовательно . Как видно, волновые функции обращаются в ноль на границах ямы. Внутри ямы они представляют собой отрезки синусоиды. Основное условие, котрое должно выполняться,- на ширине ямы должно укладываться целое количество для каждой синусоиды. Количество этих половинок определяется значением целого числа n. Анализ графиков показывает, что вероятность нахождения квантовой частицы в потенциальной яме зависит от координаты x. Так в случае n=1 наибольшая вероятность существует для центра ямы и т.д. Получили, что если у классической частицы плотность вероятности внутри потенциальной ямы всюду одинакова, то у квантовой частицы она является функцией координат. Рассмотрим Е: из граничных условий , то , где , т. е. есть множество значений энергии, которые частица не принимает. Таким образом, энергия дискретна, т. е. квантована. Чем меньше , тем выше ; состояния частицы дискретны. Энергия пробегает ряд значений, не равных 0. Разрешенные энергии частицы называются энергетическими уровнями, они появляются, если частица ограничена в пространстве. Разность энергий двух соседних уровней . С увеличением n соседние уровни удаляются друг от друга. Величина энергетического зазора между уровнями зависит также от массы частицы m и ширины ямы l. Чем меньше эти величины, тем больше расстояние между уровнями. С увеличением ширины ямы или массы частицы уровни сгущаются и их дискретность все менее заметна. В пределе беск широкой ямы или частицы с беск большой массы получаем классический непрерывный спектр энергии.

Изобразим волновую функцию на фоне уравнений при .

- основное состояние (основной энергетический уровень).

У классической частицы этот график выглядит в виде прямой, параллельной оси Ох.

Минимальное значение энергии . Состояние частицы с такой энергией называется основным состоянием. То, что квантовая частица не может иметь энергию, равную нулю согласуется с принципом неопределенности. Волновая функция и энергия состояния квантовой частицы в потенциальной яме однозначно определяются величиной целого числа n, которое определяется квантовым числом системы.

Образование молекул. Ковалентная и ионная связь.

Молекулярные структуры существуют благодаря химическим связям, которые обеспечиваются электронами валентных оболочек.

Связи образуются за счёт частичной или полной передачи валентных электронов.

1. Ковалентная связь

Обусловлена обменом парой электронов с противоположным спином.

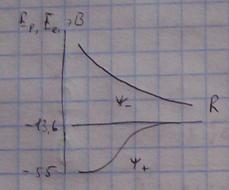
Начинаем сближать эти две ямы. Электрон может попадать из одной ямы в другую. В конце концов он перестанет различать эти две ямы и будет принадлежать двум ямам.

ψ_-=ψ₁-ψ₂

Состояние, стягивающее систему.

Состояние, разваливающее систему.

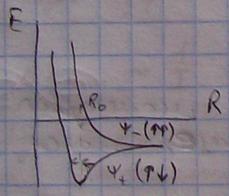
F=grad(v)

Состояние ψ₊ характеризуется minэнергии и является связывающим.

Молекула водорода образуется только в случае, если 2 электрона направлены с разнонаправленными спинами. В противном случае молекула не образуется.

Ковалентная связь является обменным взаимодействием.

Для ионной связи характерна полная передача электронов одного атома другому.

По мере объединения атомов молекулы исходного атомарного уровня расщепляются.

По мере сближения атомов снимается (?) вырождение состояний

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде

Общее решение дифференциального уравнения (220.3):

Y(x) = Asin kx + Bcos kx.

Так как по (220.2) y(x) = 0, то B = 0. Тогда

Условие (220.2) Y(l) = Asin kl выполняется только при kl = np, где n - целые числа, т. е. необходимо, чтобы

Из выражений (220.4) и (220.6) следует, что

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

Эта формула была впервые предложена Максом Планком в 1900г. и называется в его честь. Она полностью соответствует экспериментальным данным для любых длин волн. Легко проверить, что в приближении классической электродинамики Максвелла, т.е. при больших длинах волн, формула Планка переходит в классическую формулу для плотности энергии излучения (2). Более того, сам Планк первоначально фактически угадал формулу (6), анализируя графики экспериментальных кривых . Константа Планка впервые в истории науки появилась именно в этой формуле. Квантовая теория родилась, когда Планк попытался теоретически вывести формулу (6) и обнаружил, что это возможно, только еслипредположить квантование энергии излучения.

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора - системе, способной совершать гармонические колебания.История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателейгармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (гдеn = 0,1, 2,3. ) на нечто, названное им квантом энергии hυ.

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

· Колебания маятника с малой амплитудой.

· Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

· Колебания маятника с малой амплитудой.

· Другой пример – вертикальные колебания грузика, подвешенного на пружине.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Читайте также: