Битовые логические операции сообщение

Обновлено: 16.05.2024

В своё время я не мог понять смысл таких вещей, как битовые операции. Статьи в интернете не давали мне практического понимания этого вопроса. Со временем, когда я столкнулся с программированием микроконтроллеров (МК), я понял удобство подобных операций, поэтому я решил написать данную статью, чтобы пролить свет на этот вопрос людям, которые только услышали про битовые операции и хотят узнать конкретное практическое применение данных операций. Все примеры будут приведены для tms320f28027.

Операции битового сдвига:

Битовые операции, как можно понять из названия, заключаются в сдвиге битов вправо (>>) или влево (

Данная статья не подлежит комментированию, поскольку её автор ещё не является полноправным участником сообщества. Вы сможете связаться с автором только после того, как он получит приглашение от кого-либо из участников сообщества. До этого момента его username будет скрыт псевдонимом.

О песочнице

Если у вас есть приглашение, отправьте его автору понравившейся публикации — тогда её смогут прочитать и обсудить все остальные пользователи Хабра.

Чтобы исключить предвзятость при оценке, все публикации анонимны, псевдонимы показываются случайным образом.

Во многих языках программирования допустимы логические операции над битами целых чисел. В отличие от обычных логических операций, результатом выполнения которых является логический тип данных, битовые логические операции просто изменяют целое число согласно определенным правилам. Точнее битовые операции изменяют отдельные биты двоичного представления числа, в результате чего изменяется его десятичное значение.

Например, в языке программирования Паскаль обычные логические операции и логические операции над битами обозначают с помощью одних и тех же ключевых слов: not, and, or, xor . Компилятор определяет, что имелось в виду в зависимости от контекста использования этих слов. Обычные логические операции объединяют два и более простых логических выражения. Например, (a > 0) and (c != b) , (c и т.п. В свою очередь побитовые логические операции выполняются исключительно над целыми числами (или переменными, которые их содержат). Например, a and b, a or 8, not 247 .

Как понять побитовые операции

1. Переведем пару произвольных целых чисел до 256 (один байт) в двоичное представление.

2. Теперь расположим биты второго числа под соответствующими битами первого и выполним обычные логические операции к цифрам, стоящим в одинаковых разрядах первого и второго числа. Например, если в последнем (младшем) разряде одного числа стоит 1, а другого числа — 0, то логическая операция and вернет 0, а or вернет 1. Операцию not применим только к первому числу.

3. Переведем результат в десятичную систему счисления.

4. Итак, в результате побитовых логических операций получилось следующее:

Вот еще один пример выполнения логических операций над битами. Проверьте его правильность самостоятельно.

Зачем нужны побитовые логические операции

Глядя на результат побитовых операций, не сразу можно уловить закономерности в их результате. Поэтому непонятно, зачем нужны такие операции. Однако, они находят свое применение. В байтах не всегда хранятся числа. Байт или ячейка памяти может хранить набор флагов (установлен — сброшен), представляющих собой информацию о состоянии чего-либо. С помощью битовых логических операций можно проверить, какие биты в байте установлены в единицу, можно обнулить биты или, наоборот, установить в единицу. Также существует возможность сменить значения битов на противоположные.

Проверка битов

Проверка битов осуществляется с помощью битовой логической операции and .

Представим, что имеется байт памяти с неизвестным нам содержимым. Известно, что логическая операция and возвращает 1, если только оба операнда содержат 1. Если к неизвестному числу применить побитовое логическое умножение (операцию and ) на число 255 (что в двоичном представлении 1111 1111), то в результате мы получим неизвестное число. Обнулятся те единицы двоичного представления числа 255, которые будут умножены на разряды неизвестного числа, содержащие 0. Например, пусть неизвестное число 38 (0010 0110), тогда проверка битов будет выглядеть так:

Другими словами, x and 255 = x .

Обнуление битов

Чтобы обнулить какой-либо бит числа, нужно его логически умножить на 0.

Обратим внимание на следующее:

Т.е. чтобы обнулить четвертый с конца бит числа x , надо его логически умножить на 247 или на (255 - 23).

Установка битов в единицу

Для установки битов в единицу используется побитовая логическая операция or . Если мы логически сложим двоичное представление числа x с 0000 0000, то получим само число х . Но вот если мы в каком-нибудь бите второго слагаемого напишем единицу, то в результате в этом бите будет стоять единица.

Отметим также, что:

Поэтому, например, чтобы установить второй по старшинству бит числа x в единицу, надо его логически сложить с 64 ( x or 64 ).

Смена значений битов

Для смены значений битов на противоположные используется битовая операция xor . Чтобы инвертировать определенный бит числа x , в такой же по разряду бит второго числа записывают единицу. Если же требуется инвертировать все биты числа x , то используют побитовую операцию исключающего ИЛИ ( xor ) с числом 255 (1111 1111).

Операции побитового циклического сдвига

Помимо побитовых логических операций во многих языках программирования предусмотрены битовые операции циклического сдвига влево или вправо. Например, в языке программирования Паскаль эти операции обозначаются shl (сдвиг влево) и shr (сдвиг вправо).

Первым операндом операций сдвига служит целое число, над которым выполняется операция. Во втором операнде указывается, на сколько позиций сдвигаются биты первого числа влево или вправо. Например, 105 shl 3 или 105 shr 4 . Число 105 в двоичном представлении имеет вид 0110 1001.

При сдвиге влево теряются старшие биты исходного числа, на их место становятся младшие. Освободившиеся младшие разряды заполняются нулями.

При сдвиге вправо теряются младшие биты исходного числа, на их место становятся старшие. Освободившиеся старшие разряды заполняются нулями, если исходное число было положительным.

Побитовые операции (англ. bitwise operations) — операции, производимые над цепочками битов. Выделяют два типа побитовых операций: логические операции и побитовые сдвиги.

Содержание

Битовые операторы И [math](AND,\ \&)[/math] , ИЛИ [math](OR,\ \mid)[/math] , НЕ [math](NOT,\ \sim)[/math] и исключающее ИЛИ [math](XOR,\ $\textasciicircum$,\ \oplus)[/math] используют те же таблицы истинности, что и их логические эквиваленты.

Побитовое И используется для выключения битов. Любой бит, установленный в [math]0[/math] , вызывает установку соответствующего бита результата также в [math]0[/math] .

&
&	11001010 11100010
11000010

Побитовое ИЛИ используется для включения битов. Любой бит, установленный в [math]1[/math] , вызывает установку соответствующего бита результата также в [math]1[/math] .

\|
\|	11001010 11100010
11101010

Побитовое НЕ инвертирует состояние каждого бита исходной переменной.

~
~	11001010
00110101

Исключающее ИЛИ устанавливает значение бита результата в [math]1[/math] , если значения в соответствующих битах исходных переменных различны.

^
^	11001010 11100010
00101000

Операторы сдвига [math]\lt \lt [/math] и [math]<\gt \gt >[/math] сдвигают биты в переменной влево или вправо на указанное число. При этом на освободившиеся позиции устанавливаются нули (кроме сдвига вправо отрицательного числа, в этом случае на свободные позиции устанавливаются единицы, так как числа представляются в двоичном дополнительном коде и необходимо поддерживать знаковый бит).

Сдвиг влево может применяться для умножения числа на два, сдвиг вправо — для деления.

В языке программирования Java существует также оператор беззнакового битового сдвига вправо [math]\gt \gt \gt [/math] . При использовании этого оператора на освободившиеся позиции всегда устанавливаются нули.

Пусть дано число [math]x[/math] . Поскольку при сдвиге вправо на освобождающиеся позиции устанавливается бит знака, знак числа [math]x[/math] можно определить, выполнив сдвиг вправо на всю длину переменной:

Используя побитовые операции можно также узнать, различны ли знаки двух переменных [math]x[/math] и [math]y[/math] . Если числа имеют различный знак, то результат операции XOR, произведенной над их знаковыми битами, будет единицей. Поэтому неравенство [math](x \oplus y) \lt 0[/math] будет верно в том случае, если числа [math]x[/math] и [math]y[/math] разного знака.

Пусть дано число [math]x[/math] . Если [math]x[/math] положительно, то [math]mask = 0[/math] , и [math](x + mask) \oplus mask = x[/math] . В случае, если [math]x[/math] отрицательно, [math]mask = -1[/math] . Тогда получается, что мы работаем с числом [math]x[/math] так, как будто оно представлено в коде со сдвигом с тем отличием, что у нас знаковый бит принимает значение [math]1[/math] для отрицательных чисел, а [math]0[/math] — для положительных.

Этот способ корректен только если можно утверждать, что величина [math](x - y)[/math] лежит между граничными значениями типа int.

Пусть даны числа [math]x[/math] и [math]y[/math] разрядности [math]n[/math] . Тогда если [math]x \lt y[/math] , то [math]((x - y) \gt \gt (n - 1)) = -1[/math] , а если [math]x \geqslant y[/math] , то [math]((x - y) \gt \gt (n - 1)) = 0[/math] . Выражение [math]((x - y) \& ((x - y) \gt \gt (n - 1))[/math] принимает значение [math]0[/math] , если [math]x \geqslant y[/math] , и [math](x - y)[/math] , если [math]x \lt y[/math] .

Пусть дано число [math]x[/math] . Тогда, если результатом выражения [math](x\ \&\&\ !(x\ \&\ (x - 1)))[/math] является единица, то число [math]x[/math] — степень двойки.

Правая часть выражения [math](!(x\ \&\ (x - 1)))[/math] будет равна единице, только если число [math]x[/math] равно [math]0[/math] или является степенью двойки. Если число [math]x[/math] является степенью двойки, то в двоичной системе счисления оно представляется следующим образом: [math]1\underbrace_[/math] , где [math]n[/math] — показатель степени. Соответственно, выражение [math](x - 1)[/math] будет иметь вид [math]\underbrace_[/math] , и [math]x\ \&\ (x - 1)[/math] равно [math]0[/math] .

Операция логического И в данном выражении отсекает тот случай, когда [math](x = 0)[/math] и не является степенью двойки, но при этом правая часть [math](!(x\ \&\ (x - 1)))[/math] равна единице.

Пусть дано число [math]x[/math] и необходимо узнать его младший единичный бит.

Применим к числу [math]x[/math] побитовое отрицание, чтобы инвертировать значения всех его бит, а затем прибавим к полученному числу единицу. У результата первая часть (до младшего единичного бита) не совпадает с исходным числом [math]x[/math] , а вторая часть совпадает. Применив побитовое И к этим двум числам, получим степень двойки, соответствующую младшему единичному биту исходного числа [math](x\ \&\ (\sim x + 1))[/math] .

К такому же результату можно прийти, если сначала отнять от числа [math]x[/math] единицу, чтобы обнулить его младший единичный бит, а все последующие разряды обратить в [math]1[/math] , затем инвертировать результат и применить побитовое И с исходным числом [math](x\ \&\ \sim (x - 1))[/math] .

Пусть дано число [math]x[/math] и необходимо узнать его старший единичный бит.

Рассмотрим некоторое число, представим его как [math]0\dots01b \dots b[/math] , где [math]b[/math] — любое значение бита. Тогда, если совершить битовый сдвиг этого числа вправо на [math]1[/math] и произвести побитовое ИЛИ результата сдвига и исходного числа, мы получим результат [math]0\dots011b \dots b[/math] . Если мы повторим эту последовательность действий над полученным числом, но устроим сдвиг на [math]2[/math] , то получим [math]0\dots01111b \dots b[/math] . При каждой следующей операции будем увеличивать модуль сдвига до следующей степени двойки. После некоторого количества таких операций (зависит от разрядности числа) мы получим число вида [math]0\dots01\dots1[/math] . Тогда результатом выполнения действий [math]x - (x \texttt< \gt \gt >1)[/math] будет число, состоящее только из старшего бита исходного числа.

Пусть дано число [math]x[/math] и надо совершить циклический сдвиг его битов на величину [math]d[/math] . Желаемый результат можно получить, если объединить числа, полученные при выполнении обычного битового сдвига в желаемую сторону на [math]d[/math] и в противоположном направлении на разность между разрядностью числа и величиной сдвига. Таким образом, мы сможем поменять местами начальную и конечную части числа.

Для подсчета количества единичных битов в числе [math]x[/math] можно воспользоваться следующим алгоритмом:

Поскольку [math]5555_[/math] равно [math]01010101 01010101_[/math] , результатом операции [math]x\ \&\ 5555_[/math] является число, в котором все нечетные биты соответствуют нечетным битам числа [math]x[/math] . Аналогично, результатом операции [math](x\ \texttt<\gt \gt \gt >\ 1)\ \&\ 5555_[/math] является число, в котором все нечетные биты соответствуют четным битам [math]x[/math] . Четные биты результата в обоих случаях равны нулю.

Мысленно разобьем двоичную запись нашего числа [math]x[/math] на группы по [math]2[/math] бита. Результатом операции [math]x\ \&\ 5555_ + (x\ \texttt<\gt \gt \gt >\ 1)\ \&\ 5555_[/math] будет такое число, что если разбить его двоичную запись на группы по два бита, значение каждой группы соответствует количеству единичных битов в соответствующей паре битов числа [math]x[/math] .

Аналогично, число [math]3333_[/math] равно [math]00110011 00110011_[/math] и операция [math]x = (x\ \&\ 3333_) + (x\ \texttt<\gt \gt \gt >\ 2\ \&\ 3333_)[/math] , примененная к результату, полученному на первом этапе, выполняет подсчет количества единичных битов в блоках по [math]4[/math] . В свою очередь, число [math]\texttt_[/math] равно [math]00001111 00001111_[/math] и операция [math]x = (x\ \&\ \texttt_) + (x\ \texttt<\gt \gt \gt >\ 4\ \&\ \texttt_)[/math] позволяет подсчитать число единичных бит в блоках по [math]8[/math] .

Теперь необходимо просуммировать числа, записанные в блоках по [math]8[/math] битов, чтобы получить искомую величину. Это можно сделать, домножив результат на [math]0101_[/math] [math](1 00000001_)[/math] . Ответ на задачу будет находиться в первых восьми битах произведения. Выполнив сдвиг вправо на [math]8[/math] (для шестнадцатибитных чисел), мы получим долгожданный ответ.

Заметим, что операция [math]x\ \&\ 55_ + (x\ \texttt<\gt \gt \gt >\ 1)\ \&\ 55_[/math] равносильна операции [math]x - (x\ \texttt<\gt \gt \gt >\ 1)\ \&\ 55_[/math] , в чем легко убедиться, рассмотрев все числа из двух бит.

В свою очередь, операцию [math](x\ \&\ \texttt_) + ((x\ \texttt<\gt \gt \gt >\ 4)\ \&\ \texttt_)[/math] можно заменить на [math](x + (x\ \texttt<\gt \gt \gt >\ 4))\ \&\ \texttt_[/math] . Эта замена не повлияет на результат, так как максимальное значение в любой группе из четырех битов данного числа равно четырем, то есть требует только трех битов для записи, и выполнение суммирования не повлечет за собой переполнения и выхода за пределы четверок.

Таким образом, мы получили код, приведенный в начале раздела.

Чтобы получить биты числа [math]x[/math] , записанные в обратном порядке, применим следующий алгоритм.

Более подробно про то, что за константы выбраны для данного алгоритма, можно прочитать в разделе подсчет количества единичных битов.

Для работы с подмножествами удобно использовать битовые маски. Применяя побитовые операции легко сделать следующее: найти дополнение [math](\sim mask)[/math] , пересечение [math](mask_1\ \&\ mask_2)[/math] , объединение [math](mask_1 \mid mask_2)[/math] множеств, установить бит по номеру [math](mask \mid (1\ \texttt<\lt \lt >\ x))[/math] , снять бит по номеру [math](mask\ \&\ \sim(1\ \texttt<\lt \lt >\ x))[/math] .

Битовые маски используются, например, при решении некоторых задач [1] динамического программирования.

Алгоритм Флойда–Уоршелла (англ. the Floyd–Warshall algorithm) — алгоритм для нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а если же такой цикл есть, позволяет найти хотя бы один такой цикл. Асимптотическая сложность алгоритма [math] \Theta(n^3) [/math] , также требует [math] \Theta(n^2) [/math] памяти.

Дерево Фенвика (англ. Binary indexed tree) — структура данных, которая может выполнять следующие операции:

изменять значение любого элемента в массиве,
выполнять некоторую ассоциативную, коммутативную, обратимую операцию [math] \circ [/math] на отрезке [math] [i, j] [/math] .

Данная структура требует [math] O(n) [/math] памяти, а выполнение каждой операции происходит за [math] O(\log n) [/math] .

Функция, позволяющая делать операции вставки и изменения элемента за [math] O(\log n) [/math] , задается следующей формулой [math] F(i) = (i \And (i + 1)) [/math] . Пусть дан массив [math] A = [a_0, a_1, \ldots, a_][/math] . Деревом Фенвика называется массив [math] T [/math] из [math] n [/math] элементов: [math] T_i = \sum\limits_^ a_k[/math] , где [math] i = 0\ldots n - 1 [/math] и [math] F(i) [/math] — функция, которую мы определили ранее.

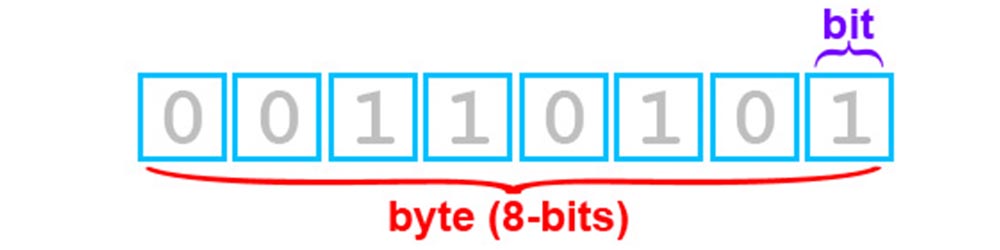
Данный урок посвящён битовым операциям (операциям с битами, битовой математике, bitmath), из него вы узнаете, как оперировать с битами – элементарными ячейками памяти микроконтроллера. Мы уже сталкивались с битовыми операциями в уроке про регистры микроконтроллера, сейчас рассмотрим всё максимально подробно. Данная тема является одной из самых сложных для понимания в рамках данного курса уроков, так что давайте разберёмся, зачем вообще нужно уметь работать с битами:

Гибкая и быстрая работа напрямую с регистрами микроконтроллера (в том числе для написания библиотек)
Более эффективное хранение данных (упаковка нескольких значений в одну переменную и распаковка обратно)
Хранение символов и другой информации для матричных дисплеев (упаковка в один байт)
Максимально быстрые вычисления
Работа со сдвиговыми регистрами и другими подобными железками
Разбор чужого кода

Данный урок основан на оригинальном уроке по битовым операциям от Arduino, можете почитать его здесь – там всё описано чуть более подробно.

Двоичная система и хранение данных

2 в степени	DEC	BIN
0	1	0b00000001
1	2	0b00000010
2	4	0b00000100
3	8	0b00001000
4	16	0b00010000
5	32	0b00100000
6	64	0b01000000
7	128	0b10000000

Таким образом, степень двойки явно “указывает” на номер бита в байте, считая справа налево (примечание: в других архитектурах может быть иначе). Напомню, что абсолютно неважно, в какой системе исчисления вы работаете – микроконтроллеру всё равно и он во всём видит единицы и нули. Если “сложить” полный байт в десятичном представлении битов, то мы получим как раз 255: 128+64+32+16+8+4+2+1 = 255. Нетрудно догадаться, что число 0b11000000 равно 128+64, то есть 192. Именно таким образом и получается весь диапазон от 0 до 255, который умещается в один байт. Если взять два байта – будет всё то же самое, просто ячеек будет 16, то же самое для 4 байт – 32 ячейки с единицами и нулями, каждая имеет свой номер согласно степени двойки. Давайте начнём манипуляции с битами с самого простого – с макро-функций, которые идут “в комплекте” с ядром Arduino.

Макросы для манипуляций с битами

В “библиотеке” Arduino.h есть несколько удобных макросов, которые позволяют включать и выключать биты в байте:

Макросы Arduino.h	Действие
bitRead(value, bit)	Читает бит под номером bit в числе value
bitSet(value, bit)	Включает (ставит 1) бит под номером bit в числе value
bitClear(value, bit)	Выключает (ставит 0) бит под номером bit в числе value
bitWrite(value, bit, bitvalue)	Ставит бит под номером bit в состояние bitvalue (0 или 1) в числе value
bit(bit)	Возвращает 2 в степени bit
Другие встроенные макросы
_BV(bit)	Возвращает 2 в степени bit
bit_is_set(value, bit)	Проверка на включенность (1) бита bit в числе value
bit_is_clear(value, bit)	Проверка на выключенность (0) бита bit в числе value

Есть ещё макрос _BV() , который сидит в других файлах ядра и в целом является стандартным макросом для других платформ и компиляторов, он делает то же самое, что bit(b) – возвращает 2 в степени b Также в ядре Arduino есть ещё два макроса для проверки состояния бита в байте, bit_is_set() и bit_is_clear() , их удобно использовать для условных конструкций с if . В целом этого уже достаточно для полноценной работы с регистрами. Так как это именно макросы, они работают максимально быстро и ничуть не хуже написанных вручную элементарных битовых операций. Чуть ниже мы разберём содержимое этих макросов и увидим, как они работают, а пока познакомимся с элементарными логическими операциями.

Битовые операции

Переходим к более сложным вещам. На самом деле они максимально просты для микроконтроллера, настолько просты, что выполняются за один такт. При частоте 16 МГц (большинство плат Arduino) одна операция занимает 0.0625 микросекунды.

Битовое И

И (AND), оно же “логическое умножение”, выполняется оператором & или and и возвращает следующее:

Основное применение операции И – битовая маска. Позволяет “взять” из байта только указанные биты:

То есть при помощи & мы взяли из байта 0b11001100 только биты 10000111, а именно – 0b11001100, и получили 0b10000100 Также можно использовать составной оператор &=

Битовое ИЛИ

ИЛИ (OR), оно же “логическое сложение”, выполняется оператором | или or и возвращает следующее:

Основное применение операции ИЛИ – установка бита в байте:

Также можно использовать составной оператор |=

Вы уже поняли, что указывать на нужные биты можно любым удобным способом: в бинарном виде (0b00000001 – нулевой бит), в десятичном виде (16 – четвёртый бит) или при помощи макросов bit() или _BV() ( bit(7) даёт 128 или 0b10000000, _BV(7) делает то же самое)

Битовое НЕ

Битовая операция НЕ (NOT) выполняется оператором ~ и просто инвертирует бит:

Также она может инвертировать байт:

Битовое исключающее ИЛИ

Битовая операция исключающее ИЛИ (XOR) выполняется оператором ^ или xor и делает следующее:

Данная операция обычно используется для инвертирования состояния отдельного бита:

То есть мы взяли бит №7 в байте 0b11001100 и перевернули его в 0, получилось 0b01001100, остальные биты не трогали.

Битовый сдвиг

Битовый сдвиг – очень мощный оператор, позволяет буквально “двигать” биты в байте вправо и влево при помощи операторов >> и , и соответственно составных >>= и Если биты выходят за границы блока (8 бит, 16 бит или 32 бита) – они теряются.

Битовый сдвиг делает не что иное, как умножает или делит байт на 2 в степени. Да, это операция деления, выполняющаяся за один такт процессора! К этому мы ещё вернёмся ниже. Посмотрите на работу оператора сдвига и сравните её с макросами bit() и _BV() :

Да, это возведение двойки в степень! Важный момент: при сдвиге дальше, чем на 15, нужно преобразовывать тип данных, например в ul: 1 даст результат 0 , потому что сдвиг выполняется в ячейке int (как при умножении, помните?). Но если мы напишем 1ul – результат будет верный.

Включаем-выключаем

Вспомним пример из пункта про битовое ИЛИ, про установку нужного бита. Вот эти варианты кода делают одно и то же:

Как насчёт установки нескольких бит сразу?

Или прицельного выключения бит? Тут чуть по-другому, используя &= и ~

Выключить несколько бит сразу? Пожалуйста!

Именно такие конструкции встречаются в коде высокого уровня и библиотеках, именно так производится работа с регистрами микроконтроллера. Вернёмся к устройству Ардуиновских макросов:

Я думаю, комментарии излишни: макросы состоят из тех же элементарных битовых операций и сдвигов!

Быстрые вычисления

Как я уже говорил, битовые операции – самые быстрые. Если требуется максимальная скорость вычислений – их можно оптимизировать и подогнать под “степени двойки”, но иногда компилятор делает это сам, подробнее смотри в уроке про оптимизацию кода. Рассмотрим базовые операции:

Деление на 2^n – сдвиг вправо на n . Например, val / 8 можно записать как val >> 3 . Компилятор не оптимизирует деление самостоятельно, что позволяет ускорить данную операцию приблизительно в 15 раз при ручной оптимизации.
Умножение на 2^n – сдвиг влево на n . Например, val * 8 можно записать как val . Компилятор оптимизирует умножение самостоятельно, поэтому в ручной оптимизации нет смысла. Но можно встретить в чужих исходниках.
Остаток от деления на 2^n – битовая маска на n младших битов. Например, val % 8 можно записать как val & 0b111 . Компилятор оптимизирует такие операции самостоятельно, поэтому в ручной оптимизации нет смысла. Но можно встретить в чужих исходниках.

Примечание: рассмотренные выше операции работают только с целочисленными типами данных!

Экономия памяти

При помощи битовых операций можно экономить немного памяти, пакуя данные в блоки. Например, переменная типа boolean занимает в памяти 8 бит, хотя принимает только 0 и 1. В один байт можно запаковать 8 логических переменных, например вот так:

Хороший трюк, может пригодиться! Я сделал удобную библиотеку для хранения битовых флагов, документация и примеры есть здесь.

Ещё интересный пример сжатия

Таким же способом можно паковать любые другие данные других размеров для удобного хранения или сжатия. Как пример – моя библиотека microLED, в которой используется следующий алгоритм: изначально необходимо хранить в памяти три цвета для каждого светодиода, каждый цвет имеет глубину 8 бит, т.е. в общей сложности тратится 3 байта на один светодиод RRRRRRRR GGGGGGGG BBBBBBBB. Для экономии места и удобства хранения можно сжать эти три байта в два (тип данных int ), потеряв несколько оттенков результирующего цвета. Например вот так: RRRRRGGG GGGBBBBB. Сожмём и упакуем: есть три переменные каждого цвета, r , g , b :

Таким образом мы отбросили у красного и синего младшие (правые) биты, в этом и заключается сжатие. Чем больше битов отброшено – тем менее точно получится “разжать” число. Например сжимали число 0b10101010 (170 в десятичной) на три бита, при сжатии получили 0b10101000, т.е. потеряли три младших бита, и в десятичной уже получится 168. Для упаковки используется битовый сдвиг и маска, таким образом мы берём первые пять битов красного, шесть зелёного и пять синего, и задвигаем на нужные места в результирующей 16-битной переменной. Всё, цвет сжат и его можно хранить. Для распаковки используется обратная операция: выбираем при помощи маски нужные биты и сдвигаем их обратно в байт:

Таким образом можно сжимать, разжимать и просто хранить маленькие данные в стандартных типах данных. Давайте ещё пример: нужно максимально компактно хранить несколько чисел в диапазоне от 0 до 3, то есть в бинарном представлении это 0b00 , 0b01 , 0b10 и 0b11 . Видим, что в один байт можно запихнуть 4 таких числа (максимальное занимает два бита). Запихиваем:

Как и в примере со светодиодами, мы просто брали нужные биты ( в этом случае младшие два, 0b11 ) и сдвигали их на нужное расстояние. Для распаковки делаем в обратном порядке:

И получим обратно наши байты. Также маску можно заменить на более удобную для работы запись, задвинув 0b11 на нужное расстояние:

Ну и теперь, проследив закономерность, можно сделать для себя функцию или макрос чтения пакета:

Где x это пакет, а y – порядковый номер запакованного значения. Выведем посмотрим:

“Трюки” с битами

На битовых операциях можно сделать очень много всего интересного, и работать оно будет очень быстро и занимать мало места. Огромный список битовых трюков и хаков можно посмотреть в этой статье, их там очень много и все с примерами. Есть ещё один небольшой сборник самых простых и полезных хаков вот здесь (английский). Его я перевёл, смотрите ниже под спойлером. Другой вариант перевода (могут быть не все трюки) можно посмотреть здесь.

Перемотка бита

Забавный алгоритм, может пригодиться: перематывает один бит слева направо, то есть формирует последовательность 0b10000000, 0b01000000, 0b00100000, 0b00010000, 0b00001000, 0b00000100, 0b00000010, 0b00000001, 0b10000000 , или 128, 64, 32, 16, 8, 4, 2, 1, 128

Целые

Установка n го бита

Выключение n го бита

Инверсия n го бита

Округление до ближайшей степени двойки

Округление вниз

Получение максимального целого

Получение минимального целого

Получение максимального long

Умножение на 2

Деление на 2

Умножение на m ую степень двойки

Деление на m ую степень двойки

Остаток от деления

Проверка равенства

Проверка на чётность (кратность 2)

Обмен значениями

Получение абсолютного значения

Максимум из двух

Минимум из двух

Проверка на одинаковый знак

Смена знака

Вернёт 2 n

Является ли число степенью 2

Остаток от деления на 2 n на m

Среднее арифметическое

Получить m ый бит из n (от младшего к старшему)

Получить m ый бит из n (от старшего к младшему)

Проверить включен ли n ый бит

Выделение самого правого включенного бита

Выделение самого правого выключенного бита

Выделение правого включенного бита

Выделение правого выключенного бита

n + 1

n – 1

Получение отрицательного значения

if (x == a) x = b; if (x == b) x = a;

Поменять смежные биты

Different rightmost bit of numbers m & n

Common rightmost bit of numbers m & n

Десятичные дроби

Примечание: хаки с float могут не работать на Ардуино! Разбить float в массив бит (unsigned uint32_t)

Читайте также: