Алгоритм евклида краткое сообщение

Обновлено: 04.07.2024

В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары. Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как евклидово кольцо. Позже алгоритм Евклида был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.

Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA [4] , широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений [5] , при построении непрерывных дробей [6] , в методе Штурма [7] . Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких как теорема Лагранжа о сумме четырёх квадратов [8] и основная теорема арифметики [9] .

Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.

Алгоритм Евклида для целых чисел

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

= r_ q_ + r_k" width="" height="" />
= r_q_+ r_n" width="" height="" />
= r_n q_n" width="" height="" />

Тогда НОД(a,b), наибольший общий делитель и , равен , последнему ненулевому члену этой последовательности.

Существование таких , то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

Пусть k — любой общий делитель чисел a и b, не обязательно наибольший, тогда ; где и — целые числа из определения.
Тогда k является также общим делителем чисел b и r, так как b делится на k по определению, а (выражение в скобках есть целое число, следовательно, k делит r без остатка)
Обратное также верно и доказывается аналогично пункту 2: любой делитель b и r так же является делителем a и b.
Следовательно, все общие делители пар чисел (a, b) и (b, r) совпадают. Другими словами, нет общего делителя у чисел (a, b), который не был бы также делителем (b, r), и наоборот.
В частности, наибольший общий делитель остается тем же самым. Что и требовалось доказать.

Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Пример

Для иллюстрации, алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала, от 1071 отнимем кратное значение 462, пока не получим разность меньше чем 462. Мы должны дважды отнять 462, (q₀ = 2), оставаясь с остатком 147

1071 = 2 × 462 + 147.

Затем от 462 отнимем кратное значение 147, пока не получим знаменатель меньше чем 147. Мы должны трижды отнять 147 (q₁ = 3), оставаясь с остатком 21.

462 = 3 × 147 + 21.

Затем от 147 отнимем кратное значение 21, пока не получим знаменатель меньше чем 21. Мы должны семь раз отнять 21 (q₂ = 7), оставаясь без остатка.

Таким образом последовательность a>b>R1>R2>R3>R4>. >Rn в данном конкретном случае будет выглядеть так:

Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462)=21.

В табличной форме, шаги были следующие

Шаг k	Равенство	Частное и остаток
0	1071 = q₀ 462 + r₀	q₀ = 2 и r₀ = 147
1	462 = q₁ 147 + r₁	q₁ = 3 и r₁ = 21
2	147 = q₂ 21 + r₂	q₂ = 7 и r₂ = 0; алгоритм заканчивается

Расширенный алгоритм Евклида и соотношение Безу

Формулы для могут быть переписаны следующим образом:

НОД

здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.

Связь с цепными дробями

Отношение допускает представление в виде цепной дроби:

$\frac ab=[q_0; q_1, q_2,\cdots,q_n]$

При этом цепная дробь без последнего члена равна отношению коэффициентов Безу , взятому со знаком минус:

$[q_0; q_1, q_2,\cdots,q_<n-1> ] = -\frac ts$
.

Последовательность равенств, задающая алгоритм Евклида может быть переписана в форме

$\begin \frac &= q_0 + \frac \\ \frac &= q_1 + \frac \\ \frac &= q_2 + \frac \\ & <>\ \vdots \\ \frac>> &= q_k + \frac> \\ & <>\ \vdots \\ \frac>> &= q_N \end$

Последнее слагаемое в правой части равенства всегда равно обратному значению левой части следующего уравнения. Поэтому первые два уравнения могут быть объединены в форме

$\frac = q_0 + \cfrac>$

Третье равенство может быть использовано чтобы заменить знаменатель выражения r₁/r₀, получим

$\frac = q_0 + \cfrac<q_1 + \cfrac>>$

Последнее отношение остатков r_k/r_k−1 всегда может быть заменено используя следующее равенство в последовательности, и так до последнего уравнения. Результатом является цепная дробь

$\frac = q_0 + \cfrac<q_1 + \cfrac<q_2 + \cfrac<\ddots + \cfrac>>> = [ q_0; q_1, q_2, \ldots , q_N ]$

В приведённом выше примере, НОД(1071, 462) было посчитано и были найдены частные q_k 2,3 и 7 соответственно. Поэтому, 1071/462 может быть записана как

$\frac<1071> = 2 + \cfrac<3 + \cfrac> = [2; 3, 7]$

Вариации и обобщения

, в которых применим алгоритм Евклида, называются евклидовыми кольцами. К ним относятся, в частности, кольца многочленов.

Обобщённый алгоритм Евклида для многочленов

Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k[x] от одной переменной над произвольным полем k, поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел, получается последовательность полиномиальных остатков (PRS).

Пример для кольца Z[x]

Пусть cont(f) по определению — НОД коэффициентов многочлена f(x) из Z[x] — содержание многочлена. Частное от деления f(x) на cont(f) называется примитивной частью многочлена f(x) и обозначается primpart(f(x)).

эти определения понадобятся для нахождения НОД двух многочленов p1(x) и p2(x) в кольце Z[x]. Для многочленов над целыми числами верно следующее:

НОД) = " width="" height="" />
НОД" width="" height="" />
, НОД) = " width="" height="" />
НОД" width="" height="" />
.

Таким образом задача отыскания НОД двух произвольных многочленов сводится к задаче отыскания НОД примитивных полиномов.

Пусть есть два примитивных многочлена p1(x) и p2(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p1(x)) = m и deg(p2(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами.

Под псевдоделением будем понимать, что самому делению предшествует умножение полинома p1(x) на " width="" height="" />
, то есть p_1(x)=p_2(x)q(x)+r_2(x)" width="" height="" />
, , где и — соответственно псевдочастное и псевдоостаток.

Итак, — (принадлежат кольцу многочленов над целыми числами), причём . Тогда алгоритм Евклида состоит из следующих шагов:

1. Вычисление НОД содержаний:

НОД" width="" height="" />
.

2. Вычисление примитивных частей:

3. Построение последовательности полиномиальных остатков:

4. Выход и возврат результата:

Если , то вернуть , иначе вернуть .

Ускоренные версии алгоритма

Одним из методов ускорения целочисленного алгоритма Евклида является использование симметричного остатка:

Одна из версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. Применение стратегии Разделяй и Властвуй позволяет уменьшить асимптотическую сложность алгоритма.

См. также

Литература

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Алгоритм Евклида" в других словарях:

Расширенный алгоритм Евклида — Алгоритм Евклида алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин. Содержание 1 История 2 Алгоритм Евклида для целых чисел … Википедия

Алгоритм Шенкса — (англ. Baby step giant step; также называемый алгоритм больших и малых шагов) в теории групп, детерминированный алгоритм дискретного логарифмирования в кольце вычетов по модулю простого числа. Для модулей специального вида данный… … Википедия

Алгоритм Фюрера — (англ. Fürer’s algorithm) быстрый метод умножения больших целых чисел. Алгоритм был построен в 2007 году швейцарским математиком Мартином Фюрером[1] из университета штата Пенсильвания как асимптотически более быстрый алгоритм, чем его… … Википедия

Евклида алгоритм — Алгоритм Евклида алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин. Содержание 1 История 2 Алгоритм Евклида для целых чисел … Википедия

Алгоритм — У этого термина существуют и другие значения, см. Алгоритм (значения). Для улучшения этой статьи желательно?: Переработать оформление в соответствии с правил … Википедия

АЛГОРИТМ — (алгорифм), единообразная математическая процедура ( рецепт ) для решения однотипных задач, выполняемая по строго определенным правилам. Применение алгоритма позволяет получить ответ типа да или нет на любой вопрос в классе задач, для решения… … Энциклопедия Кольера

Алгоритм Монтгомери — Алгоритм Монтгомери приём, позволяющий ускорить выполнение операций умножения и возведения в квадрат, необходимых при возведение числа в степень по модулю, когда модуль велик (порядка сотен бит). Был предложен в 1985 году Питером… … Википедия

ЕВКЛИДА АЛГОРИТМ — способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков. Описан в геометрической форме Евклидом … Большой Энциклопедический словарь

Евклида алгоритм — способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков. Описан в геометрической форме Евклидом. * * * ЕВКЛИДА АЛГОРИТМ ЕВКЛИДА АЛГОРИТМ, способ нахождения наибольшего общего делителя двух… … Энциклопедический словарь

ГОСТ

Существуют разные способы поиска НОД. Одним из наиболее эффективных из них является алгоритм Евклида для вычисления наибольшего общего делителя. Рассмотрим его подробнее.

Алгоритм Евклида для нахождения НОД — это последовательное деление с остатком.

На каждом этапе нахождения НОД с помощью алгоритма Евклида производится деление большего из пары двух чисел на меньшее, а остаток записывается и используется при дальнейших вычислениях в качестве нового делителя для предыдущего.

Вычисление остатка производят до тех пор, пока он не будет равен нулю, тогда последний использованный делитель и будет являться наибольшим общим делителем, полученным через алгоритм Евклида.

Пусть даны два числа a=$f_0$ и $b=f_1$, причём $f_0≥f_1$ и оба этих числа не равны нулю. Тогда если предположить, что $f_1$ равно нулю, то НОД этих двух чисел будет равен $f_0$. Рассмотрим теперь случай, когда $f_1$ не равно нулю. В этом случае остаток от деления $f_0$ на $f_1$ пусть будет $f_2$, тогда справедливо равенство:

$НОД(f_0, f_1)= НОД(f_1, f_2)$

Пусть $a$ будет частным от деления $f$ на $g$, тогда при любом целом $a$, числа $f_0$ и $f_1$ имеют те же общие делители, что и числа $f_1$ и $f_2=(f_0-a\cdot f_1)$.

То есть применение алгоритма Евклида для нахождения наибольшего общего делителя есть не что иное, как последовательная цепочка вычислений остатков и частных от деления.

Цепочку вычисления НОД с помощью алгоритма Евклида можно записать так:

$f_0=a_1 \cdot f_1 + f_2$;

$f_1=a_2 \cdot f_2 + f_3$;

Вычисления продолжаются до тех пор пока остаток $f_$ не станет равным нулю, тогда за НОД принимается $f_$.

Каждое последовательное вычисление нового остатка называется итерацией.

Рисунок 1. Алгоритм Евклида: блок-схема. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Рассмотрим пример на получение НОД через алгоритм Евклида.

Осуществите вычисление НОД с помощью алгоритма Евклида для пары $(39; 15)$

При вычислении НОД получаем последовательно пары чисел:

$НОД(3;0)$ — последняя пара является конечной, так как остаток равен нулю. Значит, наибольшим общим делителем для чисел $39$ и $15$ является число $3$.

Алгоритм Евклида: доказательство

Докажем корректность алгоритма Евклида с помощью двух этапов.

Сначала рассмотрим последний остаток $f_$, не равный нулю.

Этот остаток является делителем обоих чисел $a$ и $b$. Так как этот остаток является общим делителем, то он должен быть меньше или равен некоторому $НОД=g$.

Для того чтобы показать, что $f_$ является делителем $a$ и $b$, запишем предыдущий остаток через $f_$:

Так как последний остаток $f_=0$, то$ f_$ также должен быть делителем $f_$:

$f_=q_f_+f_$, так как он является делителем обоих слагаемых в правой части равенства.

Проведя последующие итерации, получается, что $f_$ является делителем всех предыдущих остатков, включая $a$ и $b$.

При этом ни один из предыдущих остатков не является делителем $a$ и $b$, так как деление на них происходит с остатком.

Поэтому $f_$ является общим делителем $a$ и $b$, при этом меньшим, либо равным $g$.

На втором этапе показываем, что любой общий делитель $a$ и $b$, в том числе и $g$, должен делиться на $f_$.

Возьмём любое число $c$, являющееся делителем $a$ и $b$, также оно должно быть делителем любого получающегося остатка $f_k$.

Соответственно, числа $a$ и $b$ можно представить как $a=mc$ и $b=lc$, причём $l, m$ — натуральные числа.

Получается, что $c$ является делителем $f_1$, так как $f_1=a-q_0lc=(m-q_0l)c$.

Используя аналогичные рассуждения, можно доказать, что $c$ является делителем всех остатков.

Таким образом, получается, что $НОД=g$ должен быть делителем $f_$, что значит, что $g≤f_$.

Также $g$ должен быть меньше или равен $r_$. Это и предыдущее заключение что $f_≤g$ противоречат друг другу во всех случаях, кроме $f=g$, следовательно, $g=f_$.

То есть $f_$ является НОД, полученным через алгоритм Евклида.

НОД: расширенный алгоритм Евклида

Расширенный алгоритм Евклида рассматривает НОД через линейную комбинацию этих чисел с некоторыми целыми коэффициентами.

Для иллюстрации основных алгоритмических конструкций в информатике и программировании часто применяют алгоритм Евклида. Применяя этот алгоритм, находят наибольший общий делитель двух целых чисел. Благодаря своей простоте и наглядности этот алгоритм не теряет популярности и по сей день.

Что такое алгоритм Евклида

Евклид жил в третьем веке до нашей эры в древней Греции. Он первым написал трактат по математике, в котором изложил основы планиметрии, стереометрии и теории чисел.

Рис. 1. Портрет древнегреческого математика Евклида.

Для понимания сути алгоритма вычисления НОД удобна его геометрическая трактовка.

Рассматриваются два отрезка разной длины. Из большего отрезка вычитают меньший, и затем больший отрезок заменяют результатом проведенного вычитания. Это действие выполняют несколько раз, пока отрезки не станут одинаковой длины. Полученная величина отрезков и есть наибольший общий делитель.

Этапы алгоритма Евклида

Процесс вычисления наибольшего общего делителя двух чисел удобно представить в виде цепочки шагов.

Построчная запись алгоритма Евклида

Определиться со значением первого числа X.
Определиться со значением второго числа Y.
Если X≠Y, то выполнять пункт 4, иначе перейти к пункту 5.
Если X>Y, то заменить X на X-Y и перейти к пункту 3, иначе заменить Y на Y- X и перейти к пункту 3.
Считать Х наименьшим общим делителем.

В рассмотренной последовательности используются условные конструкции и конструкция повтора.

Для наглядного представления алгоритма Евклида используется блок-схема.

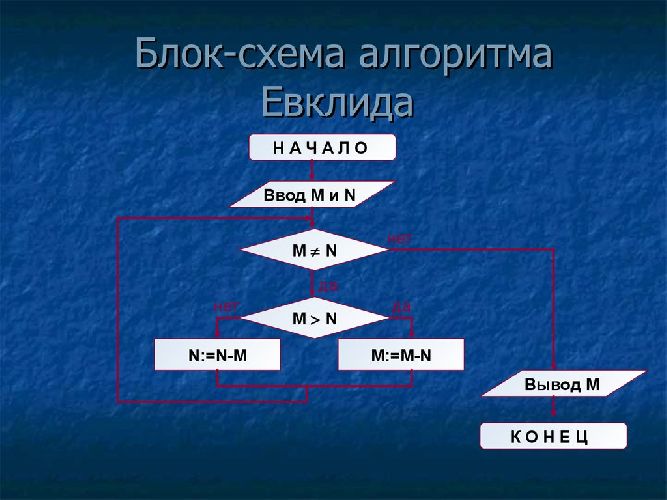
Рис. 2. Блок схема нахождения НОД по алгоритму Евклида.

Запись алгоритма Евклида на языке Паскаль

Рис. 3. Логотип интегрированной среды разработки TurboPascal.

При записи алгоритма Евклида на процедурном языке программирования Паскаль необходимо строго придерживаться структуры программы. Начинать программу необходимо с заголовка, записывая ключевое слово PROGRAM и название программы. Пусть программа называется EVKLID. В конце первой строки ставится точка с запятой. Этот знак следует ставить в конце каждой строки программы, а точнее после каждого оператора, процедуры или функции. Отсутствие его приведет к ошибке при отладке программы.

При записи алгоритма на языке программирования следует помнить правила использования ключевых слов, всегда описывать предварительно используемые переменные и не допускать синтаксических ошибок.

Описание переменных

В алгоритме используется всего две переменные X и Y, которые следует описать в разделе описания переменных, задавая им целый тип.

Var X, Y : integer;

Основная часть программы, в которой производятся все вычисления, заключается в операторные скобки begin и end. В конце программы обязательно ставится точка.

Ввод переменных с клавиатуры

Часть программы, предназначенная для ввода чисел, может выглядеть так:

write(‘Введите первое число X = ‘);

write(‘Введите второе число Y = ‘);

Организация повтора

Операцию вычитания в соответствии с алгоритмом следует выполнять до тех пор, пока выполняется условие неравности переменных X и Y. При равенстве X и Y повтор следует прекратить. Искомое число найдено.

Для реализации цикла, в котором итерации выполняются в соответствии с условием, удобнее всего использовать оператор с предусловием WHILE..DO. В решаемой задаче эта часть программы будет выглядеть так:

Запись условной конструкции на языке Паскаль

Условие на языке Паскаль записывается с помощью оператора IF..THEN..ELSE.

if X > Y then X:= X – Y else Y:= Y – X;

И в завершении программы, искомый результат выводится на экран.

Writeln (‘НОД чисел X и Y равен ‘, X);

Весь текст программы будет иметь вид:

Var X, Y : integer;

write(‘Начните вводить первое число X = ‘);

write(‘Начните вводить второе число Y = ‘);

if X > Y then X:= X – Y else Y:= Y – X;

Writeln (‘НОД чисел X и Y равен ‘, X);

Что мы узнали?

Для расчета наибольшего общего делителя двух целых чисел уже более тысячи лет используется простой и наглядный алгоритм, придуманный древнегреческим ученым Евклидом. Он хорошо иллюстрирует работу условных и циклических операторов в языке Паскаль.

Читайте также: