Чему равен объем сообщение о событии с вероятностью равной 64

Обновлено: 04.07.2024

В результате изучения данной темы вы должны будете:

названия единиц измерения информации;

формулы расчета количества информации;

переводить количество информации из одних единиц в другие;

определять информационный объем информационного объекта.

Вероятностный и алфавитный подходы к измерению информации

Измерение информации является одной из важнейших задач теоретической информатики. В курсе информатике рассматриваются два подхода к измерению информации: содержательный (вероятностный) и алфавитный.

Содержательный (Вероятностный) подход

Он основан на следующих соображениях:

те или иные события имеют некоторую вероятность (возможность произойти или не произойти);

событие, которое совершается всегда, имеет вероятность равную единице (например, восход Солнца); событие, которое не совершается никогда, имеет вероятность равную 0 (например, восход Солнца на западе); в остальных случаях вероятность совершения события есть дробное число от 0 до 1;

Вычисление количества информации для

Р.Хартли в 1928 г. сформулировал законы, которым должно подчиняться количество информации:

2) Чем больше количество возможных вариантов событий, тем больше информации

Решение этого уравнения выглядит как i =log 2 N ,

где log – функция логарифма по основанию 2 , обратная возведению значения основания логарифма в степень, равную I, т.е. из формулы Хартли следует зависимость

Для облегчения вычислений для значений N, представляющих собой степени числа 2, можно составить таблицу

Сводная таблица исчисления количества информации для равновероятных событий

Неопределённость знаний о результате N

Вероятность события 1/N

2 2,584962501. =6
log 2 6≈2,584962501

Из таблицы видно, что когда число возможных исходов событий равно целым степеням двойки, показательное уравнение решается в уме. Если же число возможных исходов событий не равно целым степеням двойки, то приходится пользоваться таблицей логарифмов.

Рассмотрим примеры заданий на вычисление количества информации равновероятных событиях

Из 4 дорожек необходимо выбрать одну, т.е. N = 4. Значит I = 2, т.к. 4 = 2 2 .

Пояснение: номер дорожки (3) не влияет на количество информации, так как вероятности событий в этих задачах мы приняли считать одинаковыми.

Вычисление количества информации для неравновероятных событий.

Если N – общее число возможных событий, из них интересующее нас событие может произойти K раз, то вероятность этого события можно оценить как K/N.

Средневзвешенное количество информации, которая может быть получена, определяется по формуле I = 1/2 * 1 бит + 1/4 * 2 бита + 1/8 * 3 бита + 1/8 * 3 бита = 1,75 бита.

В общем случае среднее количество информации, получаемой при неравновероятных событиях, определяется по формуле Шеннона:

Эту формулу можно расписать в таком виде:

Если все эти события равновероятны, т.е. р 1= р 2 =……=р N = р, то очевидно, что формула Шеннона преобразуется в формулу Хартли, которая является частным случаем формулы Шеннона.

Связь между количеством информации и вероятностью события.

Для N равновероятных событий вероятность одного отдельного события р=1/ N .

С учетом этого формула Хартли может быть преобразована в соотношение:

В этом случае вычисление количества информации можно производить по данным таблицы, представленной выше, предварительно вычислив значение N как величину, обратную значению р.

Например, для события, вероятность которого (р) составляет 0,018, получается N=1/0,018 = 55,56, тогда берется ближайшее большее значение N, кратное 2 (N=64) и по таблице определяем, что I = 6 бит.

Рассмотрим примеры заданий на вычисление количества информации при неравновероятных событиях

Синдбад-мореход в числе 10 других купцов плывёт в дальние страны на корабле с командой из 40 человек. Корабль захватили пираты, разграбили груз, разделили одежды пленников. Их привели на рынок невольников для продажи на галеры. Торг только начался. Какова вероятность пиратам продать на рынке невольников бывшего моряка? Велика ли вероятность пиратам продать на галеры бывшего купца? С какой вероятностью на галеры продадут именно Синдбада?

Обозначим вероятность (по-английски probability ) продажи бывшего купца p m , а вероятность продажи бывшего моряка p s . Тогда p m =10/50=0,2, а p s =40/50=0,8. p m / p s =1/4.Значит, вероятность продажи бывшего купца в 4 раза меньше вероятности продажи бывшего моряка.

Все возможные продажи 50 пленников составят тогда 0,2+0,8=1. Значит, поскольку Синдбад – один из 50 пленников, вероятность, что на галеры продадут именно его, равна 1/50.

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Сколько информации мы получим, когда поймаем какую-нибудь рыбу.

Найдем общее количество рыб в озере: S = 12500 + 25000 + 2*6250 = 50000.

Найдем вероятность попадания на удочку каждого вида рыб:

Ро= 12500/50000 = 0,25,

Pк = 25000 /50000 = 0,5,

Pп =6250/50000 = 0,125,

Pщ = 6250/50000 = 0,125.

3. Найдем количество информации:

i = - (0,25*log 2 0,25 + 0,5*log 2 0,5 + 0,125*log 2 0,125 + 0,125*log 2 0,125) = - (0,25*(-2) + 0,5*(-1) + 0,125*(-3) + 0,125*(-3)) = -(-0,5-0,5-0,375-0,375)= -(-1,75)= 1,75 бит.

Ответ: 1,75 бит информации.

Единицы измерения информации

В вычислительной технике бит соответствует одному двоичному разряду , который может принимать одно из двух возможных значений: 0 или 1. в качестве более крупной величины принят байт , соответствующий двоичному числу из 8 разрядов (битов). В оперативной памяти компьютера минимальный объем ячейки памяти, выделяемой для хранения какой-либо величины, как правило, равен 1 байту.

Для обозначения количества информации, больших чем байт, приняты следующие производные единицы:

1 Килобайт (Кбайт) = 2 10 байт = 1024 байт,

1 Мегабайт (Мбайт) = 2 10 Кбайт = 1024 Кбайт,

1 Гигабайт (Гбайт) = 2 10 Мбайт = 1024 Мбайт,

1 Терабайт (Тбайт) = 2 10 Гбайт = 1024 Гбайт,

1 Петабайт (Пбайт) = 2 10 Тбайт = 1024 Тбайт,

1 Экзабайт (Эбайт) = 2 10 Пбайт = 1024 Пбайт.

В отличие от одноименных приставок в кратных величинах в математике, изменение величин в вычислительной технике происходит на каждом шаге вышеуказанной шкалы на 2 10 =1024 , а не на 10 3 =1000.

Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.

Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.

Алфавит – это множество символов, используемых при записи информации.

Мощность (размер) алфавита – это полное количество символов в алфавите.

Мощность алфавита обозначается буквой N.

мощность алфавита из русских букв равна 33;

мощность алфавита из латинских букв – 26;

мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания и т.д.);

мощность двоичного алфавита равна 2.

При алфавитном подходе считается, что каждый символ текста имеет информационный вес. Информационный вес символа зависит от мощности алфавита.

Тогда в формуле N = 2 i , где

N – количество знаков в алфавите знаковой системы, I – количество информации, которое несет каждый знак .

Например , из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе

Информационная емкость знака двоичной знаковой системы составляет 1 бит.

А теперь давайте попробуем определить, какое количество информации несет буква русского алфавита (без буквы ё).

Буква русского алфавита несет 5 битов информации.

– количество информации, которое несет один знак

Определяется мощность используемого алфавита N

Определяется количество информации, приходящееся в алфавите на один его знак

если использование всех знаков равновероятно, то используется формула Хартли

если известны вероятности использования тех или иных знаков (на основе составленной таблицы частоты встречаемости этих знаков), то используется формула Шеннона.

Для решения различных задач на определение количества информации вы должны помнить следующее:

отношение количества вариантов (или чисел) N к количеству информации I, которую несет в себе один из вариантов: N=2 I

Формула Шеннона для равновероятных событий: I=log 2 N

Таблица степеней двойки, покажет сколько вариантов можно закодировать с помощью N бит:

2 Смотреть ответы Добавь ответ +10 баллов

Ответы 2

18 446 744 073 709 551 616 значений

Другие вопросы по Информатике

Вэт значение формулы =сумм(d2: d4) равно 15. чему равно значение формулы срзнач=(d1: d4), если значениеячейки d1 равно 5? надо .

Составьте программу, проверяющую, является ли последовательность из 10 целых чисел, вводимых с клавиатуры, возрастающий.

(если, например, тебе надо найти гипотенузу в прямоугольном треугольнике, то это будет выглядить так: c=sqr(a^2+b^2) ).

а(мощность алфавита)=2 в степени i

256=2 в степени i, i=8

i(объем памяти)=81920/8=10240 бит=1280 байт=1,25 килобайт

program pr1; uses crt; var mas: array[1..20,1..20] of integer; i,j,v: integer; beginclrscr; for i: =1 to 20 dofor j: =1 to 20 do readln(mas[i,j]); for i: =1 to 20 dofor j: =1 to 20 do if mas[i,j]> 0 then begin writeln(i,'-ая строка ',j,'-ый столбец'); v: =mas[i,j]; end; for i: =1 to 20 dofor j: =1 to 20 do mas[i,j]: =v; end.

можно переслать файл размером в 2 кбайта. (16 кбайт делить на частное 512 байт и 512 бит)

Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.

Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.

Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.

Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.

Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами или элементарными событиями. Исход называется благоприятствующим появлению события $А$, если появление этого исхода влечет за собой появление события $А$.

Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара.

Вероятностью события $A$ называют отношение числа $m$ благоприятствующих этому событию исходов к общему числу $n$ всех равновозможных несовместных элементарных исходов, образующих полную группу $$P(A)=\frac. \quad(1)$$

Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Итак, вероятность любого события удовлетворяет двойному неравенству $0 \le P(A) \le 1$ .

Полезные материалы

Онлайн-калькуляторы

Большой пласт задач, решаемых с помощью формулы (1) относится к теме гипергеометрической вероятности. Ниже по ссылкам вы можете найти описание популярных задач и онлайн-калькуляторы для их решений:

(в урне находится $k$ белых и $n$ черных шаров, вынимают $m$ шаров. ) (в ящике находится $k$ стандартных и $n$ бракованных деталей, вынимают $m$ деталей. ) (в лотерее участвуют $k$ выигрышных и $n$ безвыигрышных билета, куплено $m$ билетов. )

Обучающие статьи с примерами

Примеры решений на классическую вероятность

Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?

Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. Событие А достоверное.

Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?

Решение. Вынуть два шара из десяти можно следующим числом способов: .
Число случаев, когда среди этих двух шаров будут два белых, равно .
Искомая вероятность
.

Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Решение. Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. Событие, заключающееся в вынимании синего шара, невозможное.

Пример. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?

Решение. Количество элементарных исходов (количество карт) n=36. Событие А = (Появление карты червовой масти). Число случаев, благоприятствующих появлению события А, m=9. Следовательно,
.

Пример. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.

Решение. Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е.
.

Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать способами. Следовательно, число благоприятствующих исходов равно .

Изначально, будучи всего лишь собранием сведений и эмпирических наблюдений за игрой в кости, теория вероятности стала основательной наукой. Первыми, кто придал ей математический каркас, были Ферма и Паскаль.

От размышлений о вечном до теории вероятностей

Две личности, которым теория вероятностей обязана многими фундаментальными формулами, Блез Паскаль и Томас Байес, известны как глубоко верующие люди, последний был пресвитерианским священником. Видимо, стремление этих двух ученых доказать ошибочность мнения о некой Фортуне, дарующей удачу своим любимчикам, дало толчок к исследованиям в этой области. Ведь на самом деле любая азартная игра с ее выигрышами и проигрышами — это всего лишь симфония математических принципов.

Благодаря азарту кавалера де Мере, который в равной степени был игроком и человеком небезразличным к науке, Паскаль вынужден был найти способ расчета вероятности. Де Мере интересовал такой вопрос: "Сколько раз нужно выбрасывать попарно две кости, чтобы вероятность получить 12 очков превышала 50%?". Второй вопрос, крайне интересовавший кавалера: "Как разделить ставку между участниками незаконченной игры?" Разумеется, Паскаль успешно ответил на оба вопроса де Мере, который стал невольным зачинателем развития теории вероятностей. Интересно, что персона де Мере так и осталась известна в данной области, а не в литературе.

Ранее ни один математик еще не делал попыток вычислять вероятности событий, поскольку считалось, что это лишь гадательное решение. Блез Паскаль дал первое определение вероятности события и показал, что это конкретная цифра, которую можно обосновать математическим путем. Теория вероятностей стала основой для статистики и широко применяется в современной науке.

Что такое случайность

Если рассматривать испытание, которое можно повторить бесконечное число раз, тогда можно дать определение случайному событию. Это один из вероятных исходов опыта.

Опытом является осуществление конкретных действий в неизменных условиях.

Чтобы можно было работать с результатами опыта, события обычно обозначают буквами А, B, C, D, Е…

Вероятность случайного события

Чтобы можно было приступить к математической части вероятности, нужно дать определения всем ее составляющим.

Вероятность события – это выраженная в числовой форме мера возможности появления некоторого события (А или B) в результате опыта. Обозначается вероятность как P(A) или P(B).

В теории вероятностей отличают:

достоверное событие гарантированно происходит в результате опыта Р(Ω) = 1;
невозможное событие никогда не может произойти Р(Ø) = 0;
случайное событие лежит между достоверным и невозможным, то есть вероятность его появления возможна, но не гарантирована (вероятность случайного события всегда в пределах 0≤Р(А)≤ 1).

Отношения между событиями

Рассматривают как одно, так и сумму событий А+В, когда событие засчитывается при осуществлении хотя бы одного из составляющих, А или В, или обоих – А и В.

По отношению друг к другу события могут быть:

Равновозможными.
Совместимыми.
Несовместимыми.
Противоположными (взаимоисключающими).
Зависимыми.

Если два события могут произойти с равной вероятностью, то они равновозможные.

Если появление события А не сводит к нулю вероятность появление события B, то они совместимые.

Если события А и В никогда не происходят одновременно в одном и том же опыте, то их называют несовместимыми. Бросание монеты - хороший пример: появление решки – это автоматически непоявление орла.

Вероятность для суммы таких несовместимых событий состоит из суммы вероятностей каждого из событий:

Зависящие события имеют взаимное влияние, уменьшая или увеличивая вероятность друг друга.

Отношения между событиями. Примеры

На примерах гораздо проще понять принципы теории вероятностей и комбинации событий.

Опыт, который будет проводиться, заключается в вытаскивании шариков из ящика, а результата каждого опыта – элементарный исход.

Событие – это один из возможных исходов опыта – красный шар, синий шар, шар с номером шесть и т. д.

Испытание №1. Участвуют 6 шаров, три из которых окрашены в синий цвет, на них нанесены нечетные цифры, а три других – красные с четными цифрами.

Испытание №2. Участвуют 6 шаров синего цвета с цифрами от одного до шести.

Исходя из этого примера, можно назвать комбинации:

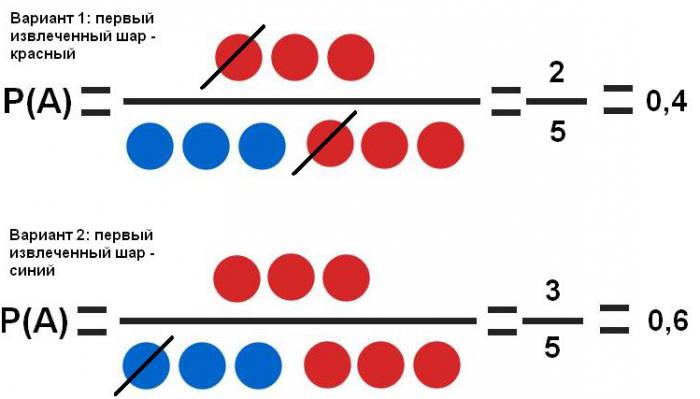
Видно, что первое событие существенно влияет на вероятность второго (40% и 60%).

Формула вероятности события

Переход от гадательных размышлений к точным данным происходит посредством перевода темы в математическую плоскость. То есть суждения о случайном событии вроде "большая вероятность" или "минимальная вероятность" можно перевести к конкретным числовым данным. Такой материал уже допустимо оценивать, сравнивать и вводить в более сложные расчеты.

Итак, формула вероятности события:

Где m – количество благоприятных исходов для события А, n – сумма всех исходов, возможных для этого опыта. При этом вероятность события всегда лежит между 0 и 1:

Расчет вероятности события. Пример

Возьмем исп. №1 с шарами, которое описано ранее: 3 синих шара с цифрами 1/3/5 и 3 красных с цифрами 2/4/6.

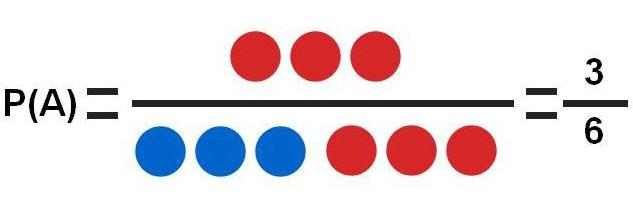
На основании этого испытания можно рассматривать несколько разных задач:

A – выпадение красного шара. Красных шаров 3, а всего вариантов 6. Это простейший пример, в котором вероятность события равна Р(А)=3/6=0,5.
B – выпадение четного числа. Всего четных чисел 3 (2,4,6), а общее количество возможных числовых вариантов – 6. Вероятность этого события равна Р(B)=3/6=0,5.
C – выпадение числа, большего, чем 2. Всего таких вариантов 4 (3,4,5,6) из общего количества возможных исходов 6. Вероятность события С равна Р(С)=4/6=0,67.

Как видно из расчетов, событие С имеет большую вероятность, поскольку количество вероятных положительных исходов выше, чем в А и В.

Несовместные события

Такие события не могут одновременно появиться в одном и том же опыте. Как в исп. №1 невозможно одновременно достать синий и красный шар. То есть можно достать либо синий, либо красный шар. Точно так же в игральной кости не могут одновременно появиться четное и нечетное число.

Вероятность двух событий рассматривается как вероятность их суммы или произведения. Суммой таких событий А+В считается такое событие, которое состоит в появлении события А или В, а произведение их АВ – в появлении обоих. Например, появление двух шестерок сразу на гранях двух кубиков в одном броске.

Сумма нескольких событий являет собой событие, предполагающее появление, по крайней мере, одного из них. Произведение нескольких событий – это совместное появление их всех.

В теории вероятности, как правило, употребление союза "и" обозначает сумму, союза "или" – умножение. Формулы с примерами помогут понять логику сложения и умножения в теории вероятностей.

Вероятность суммы несовместных событий

Если рассматривается вероятность несовместных событий, то вероятность суммы событий равна сложению их вероятностей:

Например: вычислим вероятность того, что в исп. №1 с синими и красными шарами выпадет число между 1 и 4. Рассчитаем не в одно действие, а суммой вероятностей элементарных составляющих. Итак, в таком опыте всего 6 шаров или 6 всех возможных исходов. Цифры, которые удовлетворяют условие, – 2 и 3. Вероятность выпадения цифры 2 составляет 1/6, вероятность цифра 3 также 1/6. Вероятность того, что выпадет цифра между 1 и 4 равна:

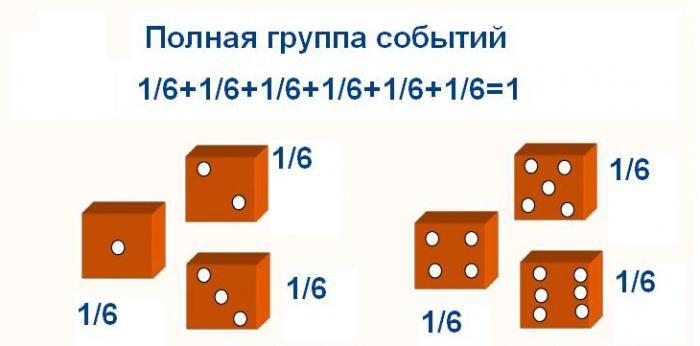
Вероятность суммы несовместимых событий полной группы равна 1.

Так, если в опыте с кубиком сложить вероятности выпадения всех цифр, то в результате получим единицу.

Также это справедливо для противоположных событий, например в опыте с монетой, где одна ее сторона – это событие А, а другая – противоположное событие Ā, как известно,

Вероятность произведения несовместных событий

Умножение вероятностей применяют, когда рассматривают появление двух и более несовместных событий в одном наблюдении. Вероятность того, что в нем появятся события A и B одновременно, равна произведению их вероятностей, или:

Например, вероятность того, что в исп. №1 в результате двух попыток два раза появится синий шар, равна

То есть вероятность наступления события, когда в результате двух попыток с извлечением шаров будет извлечены только синие шары, равна 25%. Очень легко проделать практические эксперименты этой задачи и увидеть, так ли это на самом деле.

Совместные события

События считаются совместными, когда появление одного из них может совпасть с появлением другого. Несмотря на то что они совместные, рассматривается вероятность независимых событий. К примеру, бросание двух игральных костей может дать результат, когда на обеих из них выпадает цифра 6. Хотя события совпали и появились одновременно, они независимы друг от друга – могла выпасть всего одна шестерка, вторая кость на нее влияния не имеет.

Вероятность совместных событий рассматривают как вероятность их суммы.

Вероятность суммы совместных событий. Пример

Вероятность суммы событий А и В, которые по отношению к друг другу совместные, равняется сумме вероятностей события за вычетом вероятности их произведения (то есть их совместного осуществления):

Допустим, что вероятность попадания в мишень одним выстрелом равна 0,4. Тогда событие А – попадание в мишень в первой попытке, В – во второй. Эти события совместные, поскольку не исключено, что можно поразить мишень и с первого, и со второго выстрела. Но события не являются зависимыми. Какова вероятность наступления события поражения мишени с двух выстрелов (хотя бы с одного)? Согласно формуле:

Ответ на вопрос следующий: "Вероятность попасть в цель с двух выстрелов равна 64%".

Эта формула вероятности события может быть применима и к несовместным событиям, где вероятность совместно появления события Р(АВ) = 0. Это значит, что вероятность суммы несовместных событий можно считать частным случаем предложенной формулы.

Геометрия вероятности для наглядности

Интересно, что вероятность суммы совместных событий может быть представлена в виде двух областей А и В, которые пересекаются между собой. Как видно из картинки, площадь их объединения равна общей площади за минусом области их пересечения. Это геометрическое пояснения делают более понятной нелогичную на первый взгляд формулу. Отметим, что геометрические решения – не редкость в теории вероятностей.

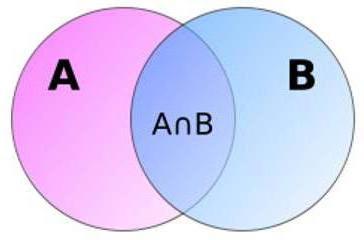
Определение вероятности суммы множества (больше двух) совместных событий довольно громоздкое. Чтобы вычислить ее, нужно воспользоваться формулами, которые предусмотрены для этих случаев.

Зависимые события

Зависимыми события называются в случае, если наступление одного (А) из них влияет на вероятность наступления другого (В). Причем учитывается влияние как появления события А, так и его непоявление. Хотя события и называются зависимыми по определению, но зависимо лишь одно из них (В). Обычная вероятность обозначалась как Р(В) или вероятность независимых событий. В случае с зависимыми вводится новое понятие – условная вероятность Р_A(В) , которая является вероятностью зависимого события В при условии произошедшего события А (гипотезы), от которого оно зависит.

Но ведь событие А тоже случайно, поэтому у него также есть вероятность, которую нужно и можно учитывать в осуществляемых расчетах. Далее на примере будет показано, как работать с зависимыми событиями и гипотезой.

Пример расчета вероятности зависимых событий

Хорошим примером для расчета зависимых событий может стать стандартная колода карт.

На примере колоды в 36 карт рассмотрим зависимые события. Нужно определить вероятность того, что вторая карта, извлеченная из колоды, будет бубновой масти, если первая извлеченная:

Очевидно, что вероятность второго события В зависит от первого А. Так, если справедлив первый вариант, что в колоде стало на 1 карту (35) и на 1 бубну (8) меньше, вероятность события В:

Если же справедлив второй вариант, то в колоде стало 35 карт, и по-прежнему сохранилось полное число бубен (9), тогда вероятность следующего события В:

Видно, что если событие А условлено в том, что первая карта – бубна, то вероятность события В уменьшается, и наоборот.

Умножение зависимых событий

Руководствуясь предыдущей главой, мы принимаем первое событие (А) как факт, но если говорить по сути, оно имеет случайный характер. Вероятность этого события, а именно извлечение бубны из колоды карт, равна:

Поскольку теория не существует сама по себе, а призвана служить в практических целях, то справедливо отметить, что чаще всего нужна вероятность произведения зависимых событий.

Согласно теореме о произведении вероятностей зависимых событий, вероятность появления совместно зависимых событий А и В равна вероятности одного события А, умноженная на условную вероятность события В (зависимого от А):

Тогда в примере с колодой вероятность извлечения двух карт с мастью бубны равна:

9/36*8/35=0,0571, или 5,7%

И вероятность извлечения вначале не бубны, а потом бубны, равна:

27/36*9/35=0,19, или 19%

Видно, что вероятность появления события В больше при условии, что первой извлекается карта масти, отличной от бубны. Такой результат вполне логичный и понятный.

Полная вероятность события

Когда задача с условными вероятностями становится многогранной, то обычными методами ее вычислить нельзя. Когда гипотез больше двух, а именно А1,А2,…,А_n, ..образует полную группу событий при условии:

Итак, формула полной вероятности для события В при полной группе случайных событий А1,А2,…,А_n равна_:

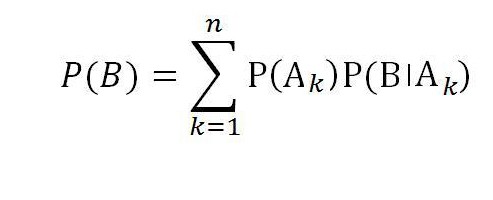
Взгляд в будущее

Вероятность случайного события крайне необходима во многих сферах науки: эконометрике, статистике, в физике и т. д. Поскольку некоторые процессы невозможно описать детерминировано, так как они сами имеют вероятностный характер, необходимы особые методы работы. Теория вероятности события может быть использована в любой технологичной сфере как способ определить возможность ошибки или неисправности.

Можно сказать, что, узнавая вероятность, мы некоторым образом делаем теоретический шаг в будущее, разглядывая его через призму формул.

Читайте также: