Знаменитые задачи древности реферат

В наши дни с помощью ЭВМ число p вычислено с точностью до миллиона знаков, что представляет скорее технический, чем научный интерес, потому что такая точность никому не нужна. Десяти знаков числа p (p =3,141592653. ) вполне достаточно для всех практических целей. Долгое время в качестве приближенного значения я использовали число 22/7, хотя уже в V в. в Китае было найдено приближение 355/113 == 3,1415929. которое было открыто вновь в Европе лишь в XVI в. В Древней Индии p считали равным =3,1622. Французский математик Ф. Виет вычислил в 1579 г. я с 9 знаками. Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда - число p , вычисленное с 32 знаками.

Но все эти уточнения значения числа л производились методами, указанными еще Архимедом: окружность заменялась многоугольником со все большим числом сторон (рис. 1,а). Периметр вписанного многоугольника при этом был меньше длины окружности, а периметр описанного многоугольника— больше. Но при этом оставалось неясным, является ли число p рациональным, т.е. отношением двух целых чисел, или иррациональным. Лишь в 1767 г. немецкий математик И. Г. Ламберт доказал, что число л иррационально, а еще через сто с лишним лет в 1882 г. другой немецкий математик— Ф. Линдеман доказал его трансцендентность , что означало и невозможность построения при помощи циркуля и линейки квадрата, равновеликого данному кругу.

Конечно, способов приближенного решения квадратуры круга с помощью циркуля и линейки было придумано великое множество. Так, в Древнем Египте было распространено правило: площадь круга равна площади квадрата со стороной, равной 8/9; p =256/81 = =3,1604.

Чрезвычайно любопытно, что квадратриса Динострата решает и вторую из знаменитых задач древности- задачу о трисекции угла. Для этого нужно отложить данный угол так, чтобы его вершина находилась в точке О, а одна из сторон совпала с лучом ОА . Из точки N пересечения квадратрисы со вторым лучом угла опускаем перпендикуляр NК на ОА, а затем делим отрезок K А на три равные части. Если восставить , в точках деления перпендикуляры к прямой ;

ОА до пересечения с квадратрисой , а затем соединить полученные точки пересечения l с точкой О, то полученные углы окажутся равными. Это следует из метода построения квадратрисы. Аналогичным образом можно делить любой угол на произвольное количество равных частей.

Напомним, что в классической постановке задачи о трисекции угла такое построение требовалось произвести лишь с помощью циркуля и линейки! В 1837 г. французский математик П. Ванцель доказал, что в общем виде задача не имеет решения, а возможно такое деление лишь в нескольких исключительных случаях, в частности для угла а = p/2 и всех углов вида p/2 n .

Решение задачи сводится к уравнению х 3 - Зх - а = 0 . Оказалось, что трисекция угла возможна для тех углов a, для которых корни этого уравнения выражаются через параметр а и целые числа лишь с помощью операций сложения, вычитания, умножения, деления и извлечения квадратного корня.

Задача об удвоении куба оказалась существенно более трудной. Если обозначить через а длину стороны исходного куба, а через х-длину стороны вдвое большего куба, то получим соотношение х 3 = 2а 3 -снова кубическое уравнение. В 1837 г. тот же П. Ванцель доказал, что невозможно построить с по мощью только циркуля и линейки отрезок, в 1/2 раз больший данного, т.е. подтвердил неразрешимость задачи удвоения куба.

Естественно, что существовали способы приближенного решения этой задачи и решения ее с помощью других инструментов и кривых. Так, уже в IV в. до н.э. древнегреческие математики умели находить корень уравнения x 3 = 2a 3 как абсциссу точки пересечения двух парабол х 2 = aу и у 2 = 2ах, а также других конических сечений.

На протяжении многих веков три знаменитые задачи древности привлекали внимание выдающихся математиков. В процессе их решения рождались и совершенствовались многие математические методы.

УДВОЕНИЕ КУБА

В этой задаче требуется построить циркулем и линейкой куб вдвое большего объёма, чем заданный. Ребро искомого куба равно а , где а - ребро исходного куба. Если принять, что а = 1, то искомое ребро х есть корень уравнения x 3 - 2 = 0. У данного уравнения нет рациональных, а значит, и квадратично-ирациональных корней. Следовательно, удвоение куба нельзя осуществить циркулем и линейкой. Примерно такое расуждение было применено в начале XIX в., когда был подготовлен необходимый для этого алгебраический аппарат.

Считают, что задача об удвоении куба появилась во времена пифагорейцев, около 540 г. до н. э. Возможно, она возникла из задачи об удвоении квадрата, которую легко решить, опираясь на теорему Пифагора, — надо построить квадрат на диагонали данного квадрата. Согласно легенде, жители Афин, на которых боги ниспослали эпидемию чумы, отправили делегацию к оракулу на остров Делос за советом, как задобрить богов и избавиться от морового поветрия. Ответ был таков:

Известна и другая легенда. Греческий комментатор VI в. до н. э. сообщает о письме, предположительно написанном царю Птолемею I. В нём говорится, что царь Минос построил на могиле сына надгробие кубической формы, но остался недоволен размерами памятника и приказал удвоить его, увеличив вдвое ребро куба. Комментатор указывает на ошибку царя Миноса (площадь поверхности памятника в результате увеличилась в четыре, а объём — в восемь раз) и рассказывает, что тогда геометры попытались решить эту задачу.

a : x =x : y = y : b

( при b=2a получаем x=a ). Эту идею удалось реализовать Платону около 340 г. до н. э. с помощью нетрадиционных чертёжных инструментов — двух прямых углов (рис. 1).

Менехм примерно в .350 г. до н. э. решал задачу об удвоении куба, используя конические сечения — кривые, по которым плоскости пересекают конус. Свои решения дали также крупнейшие древнегреческие математики Евдокс, Эратосфен, Аполлоний, Герон, Папп и др.

Одно из решений задачи об удвоении куба показано на рис. 2. Здесъ BC=BD, AB=AC=EF, а прямая l=CE параллельна АD. Полагая ВС = a, АВ = b/2, АЕ = x и СF =у, можно найти, что x и y — два средних пропорциональных а и b или что

, а

в частности, x=a при b = 2а. Все точки и линии на этой фигуре, кроме прямой АЕF, строятся циркулем и линейкой; а прямую можно провести, если разрешить метки на линейке. Хватит двух меток Е и F; их нужно сделать на расстоянии b/2 друг от друга. Тогда прямую АЕF строят, поместив линейку так, чтобы её край проходил через A, одна метка попала на l , а другая на прямую ВС.

ТРИСЕКЦИЯ УГЛА

Несложно разделить любой угол с помощью циркуля и линейки на две, а некоторые углы — и на три равные части. Последняя операция называется трисекцией угла. Например, мы можем построить треть прямого угла, поделив пополам угол правильного треугольника, а проведя биссектрису в образовавшемся угле в 30°, получим угол величиной 15° — треть угла в 45°. Есть и другие углы, для которых трисекция выполнима. Наверное, подобные построения и вселили надежду открыть способ трисекции любого угла посредством циркуля и линейки. Эту задачу пытались решить ещё в V в. до н. э. в Греции.

На рис. 3 А0В — заданный угол, из точки В проведены прямая p = ВС, перпендикулярная ОА, и прямая l , параллельная ОА. Если теперь начертить прямую а = ОРQ так, чтобы её отрезок РQ, заключённый между р и l , равнялся 20В, то угол РОС составит треть данного угла. (Это можно доказать, пользуясь тем, что треугольники ОBD и ВDQ, где О — середина РQ, равнобедренные, и теоремой о внешнем угле треугольника.) Построить прямую а можно с помощью меченой линейки, т. е. линейки, на которой нанесены две метки на расстоянии 20В друг от друга.

Никомед с той же целью чертил свою конхоиду с полюсом О, основанием p и интервалом 20В; она пересекает l в искомой точке О.

Архимед придумал свой способ трисекции. На данный угол — это угол AОВ между радиусами окружности. С помощью меченой линейки проведём прямую через точку А так, чтобы её отрезок РQ между окружностью и продолжением прямой ВО равнялся радиусу окружности. Как и на рис. 3, здесь образуются равнобедренные треугольники ОАР и ОРQ, и легко доказать, что угол ОQA втрое меньше данного.

Гиппий Элидский (около 420 г. до н. э.) для трисекции угла использовал кривую, впоследствии названную квадратрисой Динострата, который позже использовал её для решения квадратуры круга.

Квадратриса получается следующим образом. Пусть дана окружность радиуса а . Начнем вращать радиус ОА с угловой скоростью p /2 вокруг точки О - центра окружностии одновременно равномерно перемещать влево со скоростью а вертикальную прямую от точки А к точке С. Точка М их пересечения и будет описывать квадратрису. Если взять за оси координат прямую ОА и прямую 0В, то в момент времени t точка М будет иметь координаты

При стремлении t к 1 точка М стремится, к точке Р, при этом абсцисса точки М стремится к нулю, а у ординаты один множитель стремится к нулю, а другой - к бесконечности. Их произведение будет стремиться к числу 2а/ p , поэтому длина отрезка ОР равна 2a/p. Следовательно, имеет место соотношение АС/ОР=p.

Пусть теперь дана окружность радиуса г. Тогда имеем соотношение 2 pr /2r = АС/ОР, в котором известны АС, ОР и 2r-диаметр данной окружности. По ним мы можем построить отрезок, равный 2r- длине окружности, это будет четвертый пропорциональный отрезок к известным трем.

Французский математик П. Ванцель в 1837 г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой. Пусть b = a/3. По известной формуле, соs a = = 4 соs 3 b - 3 соs b. Тогда для величины х = 2 сов b получается уравнение x 3 – 3x - а = 0, где а = 2 соs a . Геометрическая задача трисекции данного угла а циркулем и линейкой разрешима тогда и только тогда, когда полученное алгебраическое уравнение разрешимо в квадратных радикалах. Возьмём, например, a = 60°. Тогда уравнение примет вид х 3 – 3x - 1 = 0. Оно неразрешимо в квадратных радикалах, а потому и трисекция с помощью циркуля и линейки в данном случае невозможна. Тем более она невозможна в общем случае. Интересно, что вообще для углов вида Зб0°/ n с целым п трисекцию удаётся осуществить тогда и только тогда, когда n не делится на 3.

КВАДРАТУРА КРУГА

В задаче о квадратуре круга требуется построить циркулем и линейкой квадрат, равновеликий данному кругу. Вероятно, задача была известна уже за две тысячи лет до н. э. в Древнем Египте и Вавилоне. Но первая прямая ссылка на неё относится к V в. до н. э. По свидетельству древнегреческого историка Плутарха, философ Анаксагор, коротая время в тюрьме, пытался квадрировать круг, т. е. превратить его в равновеликий квадрат. Если считать радиус данного круга равным 1, то сторона искомого квадрата должна составить .

Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Однако древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими. К числу таких задач относятся так называемые три знаменитые классические задачи древности:

о квадратуре круга о трисекции угла

о удвоении S круга.

Задача о квадратуре круга

Одной из древнейших и самых популярных математических задач, занимавшей умы людей на протяжении 3 – 4 тысячелетий, является задача о квадратуре круга , т.е. о построении с помощью циркуля и линейки квадрата, равновеликому данному кругу. Если обозначить радиус круга через r , то речь будет идти о построении квадрата, площадь которого равна r 2 , а сторона равна r . Теперь известно, что число -отношение окружности к своему диаметру – число иррациональное, оно выражается бесконечной непериодической десятичной дробью 3,1415926… было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.

Шенкс вычислял. Следовательно, он стоял в противоречии с требованиями задачи о квадратуре круга, где требовалось найти решение построением. Работа, сделанная Шенксом, в сущности бесполезна – или почти бесполезна. Но, с другой стороны, она может служить довольно убедительным доказательством противного тому, кто, убедившись доказательствами Линдеманна и др. или не зная о них, до сих пор ещё надеется, что можно найти точное отношение длины окружности к диаметру. Можно вычислить приближенное значение (и корня квадратного из ), удовлетворяющее тем или иным практическим потребностям. Однако не в практическом отношении интересовала людей задача о квадратуре круга, а интересовала её принципиальная сторона: возможно ли точно решить эту задачу, выполняя построения с помощью только циркуля и линейки.

Возьму линейку, проведу прямую,

И мигом круг квадратом обернётся,

Посередине рынок мы устроим,

А от него уж улицы пойдут –

Ну, как на Солнце! Хоть оно само

И круглое, а ведь лучи прямые.

Эти стихи говорят о том, что задача уже была к тому времени очень популярна в Греции. Один из современников Сократа – софист Антифон считал, что квадратуру круга можно осуществить следующим образом: впишем в круг квадрат и, разделяя пополам дуги, соответствующие его сторонам, построим правильный вписанный восьмиугольник, затем шестнадцати угольник и т.д., пока не получим многоугольник, который в силу малости сторон сольётся с окружностью. Но так как можно построить квадрат равновеликий любому многоугольнику, то и круг можно квадрировать. Однако уже Аристотель доказал, что это будет только приближённое, но не точное решение задачи, так как многоугольник никогда не может совпасть с кругом.

Фигуры-мениски ALBM и ADCE, ограниченными круговыми дугами, и называются луночками.

По теореме Пифагора:

Отношение площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров , которые в силу (1) равно 2. Итак, площадь сектора OAC ровна площади полукруга, построенного на диаметре . Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC ровна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадрату, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось.

Различные другие, продолжавшиеся в течение тысячелетий попытки найти квадратуру круга оканчивались неудачей. Лишь в 80-х годах 19в. было строго доказано, что квадратура круга с помощью циркуля и линейки невозможна. Задача о квадратуре круга становится разрешимой, если применять, кроме циркуля и линейки, еще другие средства построения. Так, еще в 4в. до н.э. греческие математики Динострат и Менехм пользовались для решения задачи одной кривой, которая была найдена еще в 5в. до н.э. Гиппием Элидским. Однако ученых Древней Греции и их последователей такие решения, находящиеся за пределами применения циркуля и линейки, не удовлетворяли. Будучи вначале чисто геометрической задачей, квадратура круга превратилась в течение веков в исключительно важную задачу арифметико-алгебраического характера, связанную с числом , и содействовала развитию новых понятий и идей в математике.

Задача о трисекции угла

Знаменитой была в древности и задача о трисекции угла ( от латинских слов tria– три и section – рассечение , разрезание), т.е.о разделении угла на три равные части с помощью циркуля и линейки. Говорят, что такое ограничение вспомогательных приборов знаменитым греческим философом Платоном.

Так, деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60 о . Пусть требуется разделить на три равные части прямой угол MAN (Рис. 2). Откладываем на полупрямой произвольный отрезок , на котором строим равносторонний треугольник ACB . Так как угол Рис. 2 CAB

равен 60 о , то = 30 о . Построим биссектрису

угла САВ , получаем искомое деление прямого угла MAN

на три равных угла: , , .

Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла (например, для углов в , п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.

Рис. 3, а, б, в: конхоида Никомеда

Задача о трисекции угла становится разрешимой и общем случае, если не ограничиваться в геометрических построениях одними только классическими инструментами, циркулем и линейкой. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э. Так, например, Гиппий Элидский, знаменитый софист, живший около 420 г. до н.э., пользовался для трисекции угла квадратрисой. Александрийский математик Никомед ( II в. до н.э.) решил задачу о трисекции угла с помощью одной кривой, названной конхоидой Никомеда (рис. 3), и дал описание прибора для черчения этой кривой.

Вот ещё одно решение задачи о три секции угла при помощи линейки с двумя насечками предложенное Кемпе:

Пусть дан какой – либо угол ABC (Рис. 6); и пусть на лезвии нашей линейки обозначены 2 точки, P и Q (см. ту же фигуру, внизу)

На одной из сторон угла откладываем от вершины B прямую BA = PQ . Делим ВА пополам в точке М ; проводим линии Рис. 6 и .

Возьмём теперь нашу линейку и приспособим её к уже полученной фигуре так, чтобы точка Р

линейки лежала на прямой КМ , точка Q лежала бы

на прямой LM , и в тоже время продолжение PQ линейки проходило бы через вершину данного угла В . тогда прямая ВР и есть искомая, отсекающая третью часть угла В .

Доказательство

как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM . Точка N есть середина гипотенузы прямоугольного треугольника PQM , а потому PN = N М , а следовательно, треугольник PNM равнобедренный, и значит

Приведённое выше решение задачи принадлежит Кемпле, который при этом поднял вопрос, почему Евклид не воспользовался делением линейки и процессом её приспособления для доказательства 4-й теоремы своей первой книги, где вместо этого он накладывает стороны одного треугольника на стороны другого. На это может ответить только, что в задачу Евклида и не входило отыскивание некоторой точки по средствам измерения и процесса приспособления линейки. В своих рассуждениях и доказательствах он просто накладывает фигуру на фигуру – и только.

Задача об удвоении куба

Удвоение куба – так называется третья классическая задача древнегреческой математики. Эта задача на ряду с двумя первыми сыграла большую роль в развитии математических методов.

Задача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению

x 3 = 2a 3 , илиx =

Задача является естественным обобщением аналогичной задачей об удвоении квадрата, которая решается просто: стороной квадрата, площадь которого равна 2а 2 , служит отрезок длиной а , т.е. диагональ данного квадрата со стороной а . Наоборот удвоение куба, объём которого равен 2а 3 , т.е. отрезок х , равный , не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX в.

а : х = х : у = у : b (1)

Суть одного механического решения задач об удвоении куба, относящегося к IVв. до н.э. , основано на методе двух средних пропорциональных. Отложим на стороне прямого угла отрезок =а , где а - длина ребра куба (рис.7), а на другой его стороне – отрезок =2а . На продолжениях сторон прямого угла стараемся найти такие точки M иN , чтобы (АМ) и (В N ) были перпендикулярны к ( MN ) ; тогда (х) и(у) будут двумя серединами пропорциональными между отрезками и . Для этого устраивается угольник с подвижной линейкой. Линейку располагают так, как показано на рисунке.

а : х = х : у = у : 2а.

Это значит что отрезок искомый.

Первые задачи на построение возникли из хозяйственных потребностей человека. Уже древним архитекторам и земледельцам приходилось решать простейшие задачи на построение, связанные с их профессией .К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.

Задачи на построение нашли широкое распространение в древней Греции ,где впервые создалась геометрическая теория в систематическом изложении.

Первым греческим ученым ,который занимался решением геометрических задач на построение, был Фалес Милетский(624-547 годы до н.э.).Это он, пользуясь построением треугольников ,определил расстояние, недоступное для непосредственного измерения-от берега до корабля в море .Это он вычислил высоту египетской пирамиды по отбрасываемой ею тени.

Большую роль в развитии задач на построение сыграл Пифагор(около 580-500 годов до н.э.).По свидетельству греческого историка математики Прокла(412-485 годы),Пифагор впервые разработал принцип геометрии и теоремы невещественным разумным путем .С именем Пифагора связана теорема, согласно которой в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов .По-видимому, эту теорему сам Пифагор (или его ученики) доказывал при помощи геометрических построений, опираясь на понятие равновеликости равносоставленных фигур.

Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению. Эти задачи следующие:

1. Задача о квадратуре круга.
Требуется построить квадрат ,площадь которого равнялась бы данному кругу.

2. Задача о трисекции угла.
Требуется произвольный угол разделить на три равные части.

3. Задача об удвоении куба.
Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.

Предварительный просмотр:

НАУЧНЫЙ руководитель:
ЖДАНОВИЧ ЕЛЕНА ИВАНОВНА,

Учитель I категории

1. Введение.
2. Цели и задачи проекта.
3. Задача о квадратуре круга.
4. Задача о трисекции угла.
5. Делосская задача об удвоении куба.
6. Заключение.
7. Литература.

Первые задачи на построение возникли из хозяйственных потребностей человека. Уже древним архитекторам и земледельцам приходилось решать простейшие задачи на построение, связанные с их профессией .К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.

Задачи на построение нашли широкое распространение в древней Греции ,где впервые создалась геометрическая теория в систематическом изложении.

Первым греческим ученым ,который занимался решением геометрических задач на построение, был Фалес Милетский(624-547 годы до н.э.).Это он, пользуясь построением треугольников ,определил расстояние, недоступное для непосредственного измерения-от берега до корабля в море .Это он вычислил высоту египетской пирамиды по отбрасываемой ею тени.

Большую роль в развитии задач на построение сыграл Пифагор(около 580-500 годов до н.э.).По свидетельству греческого историка математики Прокла(412-485 годы),Пифагор впервые разработал принцип геометрии и теоремы невещественным разумным путем .С именем Пифагора связана теорема, согласно которой в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов .По-видимому, эту теорему сам Пифагор (или его ученики) доказывал при помощи геометрических построений, опираясь на понятие равновеликости равносоставленных фигур.

Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению. Эти задачи следующие:

1.Задача о квадратуре круга.

Требуется построить квадрат ,площадь которого равнялась бы данному кругу.

Требуется произвольный угол разделить на три равные части.

Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.

2. Цели и задачи.

Данную тему моей работы я считаю актуальной, потому что очень полезно изучать историю возникновения, методы решений данных задач древними учеными, так как большинство методов и способов решений различных задач сохранились и до наших дней и используются в современной математике.

Я хотел больше узнать об истории возникновения задач, способах решения этих задач древними учеными.

Целью моей работы будет углубление в историю математики, изучение истории возникновения классических задач древности и некоторые способы их решения.

Перед собой я поставил следующие задачи:

1.Изучить литературу и источники по данной теме.

2.Обработать полученную информацию.

3.Сделать вывод и продолжить в дальнейшем изучение данной темы.

3.Задача о квадратуре круга.

Задача о квадратуре круга-самая старая из всех математических задач.Она возникла на заре человеческой культуры и ее история охватывает период около четырех тысяч лет. Этой задачей раньше греков занимались вавилоняне и египтяне. Независимо от греков ею занимались китайцы и индийцы.

Задача о квадратуре круга вместе с тем является самой популярной из всех математических задач.

Древнегреческие ученые стремились задачу о квадратуре круга решить при помощи циркуля и линейки. Показательна в этом отношении работа Гиппократа Хиоского, которому удалось криволинейную фигуру( гиппократовы луночки ) преобразовать в равновеликий ей многоугольник. Однако преобразовать круг в равновеликий ему квадрат Гиппократу так и не удалось. Остановимся несколько подробнее на его рассуждениях.

На отрезке АВ, как на диаметре, построим полукруг АСВ. Далее, из точки О- середины отрезка АВ-восстановим перпендикуляр ОС. Соединим прямыми точку С с точками А и В. Отрезок СВ будет стороной квадрата, вписанного в круг, и площадь треугольника АСВ будет равняться половине этого квадрата. НА отрезке СВ, как на диаметре, опишем еще полукруг СВЕ. Применяя к прямоугольному треугольнику АСВ теорему Пифагора, получим:

АВ 2 = АС 2 +СВ 2 =2СВ 2 (1)

На основании того, что площади кругов относятся между собой, как квадраты их диаметров, будем иметь :

пл. круга АСВ: пл. круга СВЕ= =АВ 2 : СB 2 (2) или, учитывая(1),

пл. круга АСВ: пл. круга СЕВ=2:1 (3)

пл. круга АСВ= 2 пл. круга СЕВ (4)

пл. полукруга АСВ= 2 пл. полукруга СЕВ(5)

пл. сек тора ОСВ= пл. полукруга СЕВ. (6)

Вычитая из левой правой частей равенства (6) сегмент СДВ , получим , что площадь треугольника ОСВ равняется площади луночки СДВЕ . Наконец, при помощи циркуля и линейки теперь не составляет большого труда построить квадрат ,площадь которого будет равна площади треугольника ОСВ , а следовательно , и площади луночки СДВЕ . Так Гиппократ Хиосский весьма оригинальным приемом нашел квадратуру некоторой , специального вида , луночки .

Сам Гиппократ , найдя квадратуру указанной выше луночки , пытался найти квадратуру круга .

Однако в рассуждениях Гиппократа Хиосского допущена одна ошибка, которая « из невозможного делает возможным ,- неразрешимую задачу о квадратуре круга разрешимой . Ошибка в рассуждениях Гиппократа , приводящая к иллюзорному решению задачи о квадратуре круга , была замечена еще древними учеными . Об этой ошибке говорят древнегреческий историк математики Евдем Родосский и знаменитый основоположник формальной логики Аристотель . Так , Евдем Родосский заявляет , что хотя рассуждения Гиппократа и является остроумным , тем не менее оно является ошибочным . Дело в том , говорит Евдем, что три луночки , которые рассматривал Гиппократ при решении квадратуры круга ,построены не на катетах прямоугольного треугольника , а на сторонах трапеции и , следовательно , к ним он не может применить то свойство о квадрируемости луночки, которое он доказал в начале . В этом же упрекал Гиппократа и Аристотель . Аристотель считал , что Гиппократ совершил грубую ошибку , полагая возможным квадратуру луночки, построенной на стороне квадрата, необдуманно применить к квадратуре луночки, построенной на стороне шестиугольника.

Другая попытка решить задачу о квадратуре круга с помощью циркуля и линейки была предпринята древнегреческим ученым Антифоном . Он в данный круг, квадратура которого находилась , вписывал сначала квадрат. Затем дуги , хордами которых являются стороны вписанного в круг квадрата , он делил пополам и точки деления соединял с вершинами квадрата и таким образом получал вписанный в круг правильный восьмиугольник. Далее, дуги , хордами которых являются стороны вписанного в круг правильного восьмиугольника, делил также пополам и точки деления соединял с вершинами указанного восьмиугольника и получал вписанный в круг правильный 16-угольник. Продолжая этот процесс дальше, он получал вписанные в круг правильные 32-угольник, 64-угольник и т.д. Он считал, что указанным построением, выполняемым только при помощи циркуля и линейки, можно прийти к такому правильному многоугольнику, правда, быть может, с очень большим числом сторон, который полностью исчерпает круг, то есть его площадь будет равна площади данного круга. А так как для любого правильного многоугольника всегда можно построить равновеликий ему квадрат, то и для данного круга, поскольку он исчерпывается правильным многоугольником, можно построить равновеликий ему квадрат.

Еще в древности ученые подвергли решение Антифона резкой критике. Они совершенно правильно заявляли, что утверждение Антифона, будто правильный многоугольник может совпасть с кругом, противоречит основным началам геометрии. Попытки древнегреческих ученых решить задачу о квадратуре круга путем проведения прямых и окружностей так и не увенчались успехом. Задача о квадратуре круга оказывается неразрешимой при помощи циркуля и линейки.

4. Задача о трисекции угла.

Р. Декарт был первым ученым, который высказал предположение, что трисекция произвольного угла не может быть выполнена при помощи циркуля линейки, если последняя не имеет никаких отметок. Строгое же доказательство неразрешимости задачи о трисекции произвольного угла впервые было дано в 1837 году П. Ванцелем.

5. Делосская задача об удвоении куба .

Задача об удвоении куба основывается на двух легендах. Первая легенда принадлежит Эратосфену (276-194 годы до н.э.), знаменитому греческому математику, астроному и философу. Вот что он рассказывал о причинах, побудивших рассматривать задачу об удвоении куба.

Однажды на острове Делосе, что находится в Эгейском море, вспыхнула эпидемия чумы. Жители этого острова обратились к знаменитому дельфийскому оракулу, который служил при храме Аполлона в Дельфах ( Дельфы – общегреческий религиозный центр в Фохиде, у подножия горы Парнас ), за помощью и советом.

Чтобы прекратить страдания людей, ответил им оракул, надо снискать милость богов, а для этого надо удвоить золотой жертвенник богу Аполлону ( богу Солнца ), имеющий форму куба.

Жители Делоса поспешили скорей отлить из золота два таких жертвенника, какой был установлен в храме Аполлона, и поставили один сверх другого, думая, что проблема удвоения кубического жертвенника ими решена.

Однако чума не прекращалась. Тогда они опять обратились к оракулу с недоумевающим вопросам:

-Почему же не прекращается чума, ведь мы удвоили золотой жертвенник всесильному Аполлону?

На это им оракул с огорчением ответил:

-Нет, вы не решили поставленной задачи! Надо было удвоить жертвенник, не изменяя его кубической формы.

Не в состоянии решить эту задачу так, как требовал оракул, делосцы обратились за помощью к знаменитому математику и философу Платону. Но он уклончиво ответил им:

-Боги, вероятно, недовольны вами за то, что вы мало занимаетесь геометрией.

Вторая легенда гласит: Царь Минос повелел воздвигнуть памятник своему сыну Главку. Архитекторы дали памятнику форму куба, ребро которого равнялось 100 локтям. Но Минос нашел этот памятник слишком малым и приказал его удвоить. Чувствуя свое бессилие в решении поставленной задачи, архитекторы обратились за помощью к ученым-геометрам, но и они не могли решить указанной задачи.

Древние греки сравнительно легко решили задачу об удвоении квадрата .Для этого надо уметь строить при помощи циркуля и линейки корень квадратный из двух. Если сторона данного квадрата равняется а, а сторона искомого квадрата х, то, согласно условию задачи, будем иметь:

Х 2 = 2 а 2 , откуда х=а √2 . Чтобы построить √2, нужно построить гипотенузу равнобедренного треугольника, у которого каждый катет равен единице. Теперь остается отрезок, равный √2, увеличить в а раз, тогда и получим сторону искомого квадрата. А проще всего в качестве х взять диагональ данного квадрата, которая, по теореме Пифагора, как раз и будет равняться а√2.

Обобщая задачу об удвоении квадрата, древние греки перешли к рассмотрению задачи об удвоении куба и также стремились решить ее при помощи циркуля и линейки. Оказалось, что решение задачи об удвоении куба сводится к геометрическому построению корня кубического из двух. Если ребро данного куба положить равным а, а ребро искомого куба- х, то, согласно условию задачи, будем иметь:

Х³=2а³, откуда х=а ³√2. Однако все старания построить ³√2 циркулем и линейкой не увенчались успехом. И , трудно сказать, как долго еще продолжались бы эти попытки, если бы, наконец, в первой половине 19 века не было доказано, что при помощи циркуля и линейки, без привлечения других вспомогательных средств, ³√2 построить нельзя.

Все старания решить три знаменитые задачи при известных ограничивающих условиях (циркуль и линейка) привели к доказательству, что подобное решение невозможно. Иной, пожалуй, по этому поводу скажет, что, следовательно, работа сотен умов, пытавшихся в течении столетий решить задачу, свелась ни к чему. Но это будет неверно. При попытках решить эти задачи было сделано огромное количество открытий ,имеющих гораздо больший интерес и значение, чем сами поставленные задачи.

Древность завещала решение всех трех задач нашим временам.

Выполнив эту работу, я узнал много нового и интересного о знаменитых классических задачах древности, о людях, посвятивших себя решению данных задач, методами их решения.

Изучив весь материал, я понял, что все старания решить три знаменитые задачи с помощью циркуля и линейки привели только к доказательству, что подобное решение невозможно.

1.С. Акимова. Занимательная математика.Тригон.Санкт-Петербург,1998

2.Энциклопедический словарь юного математика. Москва. Педагогика. 1989

3.Школьная энциклопедия .Математика. Москва. Большая Российская энциклопедия.1996

КЛАССИЧЕСКИЕ ЗАДАЧИ ДРЕВНОСТИ

Древнегреческие математики достигли чрезвычайно большого искусства в геометрических построениях с помощью циркуля и линейки. Однако три задачи не поддавались их усилиям. Прошли тысячелетия, и только в наше время, наконец, были получены их решения.

История нахождения квадратуры круга длилась четыре тысячелетия, а сам термин стал синонимом неразрешимых задач. Как следует из подобия кругов, отношение длины окружности к ее диаметру есть величина постоянная, не зависящая от радиуса круга, она обозначается буквой п. Таким образом, длина окружности круга радиуса r равна 2pr 2 , а так как площадь круга равна S = 2pr 2 , то задача о квадратуре круга сводится к задаче построения треугольника с основанием 2pr 2 и высотой r. Для него потом уже без труда может быть построен равновеликий квадрат.

т.е. 3,1408 p 3,1429.

В наши дни с помощью ЭВМ число p вычислено с точностью до миллиона знаков, что представляет скорее технический, чем научный интерес, потому что такая точность никому не нужна. Десяти знаков числа p (p =3,141592653. ) вполне достаточно для всех практических целей. Долгое время в качестве приближенного значения я использовали число 22/7, хотя уже в V в. в Китае было найдено приближение 355/113 == 3,1415929. которое было открыто вновь в Европе лишь в XVI в. В Древней Индии p считали равным =3,1622. Французский математик Ф. Виет вычислил в 1579 г. я с 9 знаками. Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда - число p , вычисленное с 32 знаками.

Но все эти уточнения значения числа л производились методами, указанными еще Архимедом: окружность заменялась многоугольником со все большим числом сторон (рис. 1,а). Периметр вписанного многоугольника при этом был меньше длины окружности, а периметр описанного многоугольника— больше. Но при этом оставалось неясным, является ли число p рациональным, т.е. отношением двух целых чисел, или иррациональным. Лишь в 1767 г. немецкий математик И. Г. Ламберт доказал, что число л иррационально, а еще через сто с лишним лет в 1882 г. другой немецкий математик— Ф. Линдеман доказал его трансцендентность , что означало и невозможность построения при помощи циркуля и линейки квадрата, равновеликого данному кругу.

Конечно, способов приближенного решения квадратуры круга с помощью циркуля и линейки было придумано великое множество. Так, в Древнем Египте было распространено правило: площадь круга равна площади квадрата со стороной, равной 8/9; p =256/81 = =3,1604.

Были найдены и другие пути определения квадратуры круга: кроме циркуля и линейки использовали другие инструменты или специально построенные кривые. Так, в V в. до н.э. греческий математик Гиппий из Элиды изобрел кривую, впоследствии получившую название квадратрисы Динострата (ее назвали по имени другого древнегреческого математика, жившего несколько позже и указавшего способ построения квадратуры круга при помощи этой кривой).

Чрезвычайно любопытно, что квадратриса Динострата решает и вторую из знаменитых задач древности- задачу о трисекции угла. Для этого нужно отложить данный угол так, чтобы его вершина находилась в точке О, а одна из сторон совпала с лучом ОА . Из точки N пересечения квадратрисы со вторым лучом угла опускаем перпендикуляр N К на ОА, а затем делим отрезок K А на три равные части. Если восставить , в точках деления перпендикуляры к прямой ;

ОА до пересечения с квадратрисой , а затем соединить полученные точки пересечения l с точкой О, то полученные углы окажутся равными. Это следует из метода построения квадратрисы. Аналогичным образом можно делить любой угол на произвольное количество равных частей.

Напомним, что в классической постановке задачи о трисекции угла такое построение требовалось произвести лишь с помощью циркуля и линейки! В 1837 г. французский математик П. Ванцель доказал, что в общем виде задача не имеет решения, а возможно такое деление лишь в нескольких исключительных случаях, в частности для угла а = p/2 и всех углов вида p/2 n .

Решение задачи сводится к уравнению х 3 - Зх - а = 0 . Оказалось, что трисекция угла возможна для тех углов a , для которых корни этого уравнения выражаются через параметр а и целые числа лишь с помощью операций сложения, вычитания, умножения, деления и извлечения квадратного корня.

Задача об удвоении куба оказалась существенно более трудной. Если обозначить через а длину стороны исходного куба, а через х-длину стороны вдвое большего куба, то получим соотношение х 3 = 2а 3 -снова кубическое уравнение. В 1837 г. тот же П. Ванцель доказал, что невозможно построить с по мощью только циркуля и линейки отрезок, в 1/2 раз больший данного, т.е. подтвердил неразрешимость задачи удвоения куба.

Естественно, что существовали способы приближенного решения этой задачи и решения ее с помощью других инструментов и кривых. Так, уже в IV в. до н.э. древнегреческие математики умели находить корень уравнения x 3 = 2a 3 как абсциссу точки пересечения двух парабол х 2 = a у и у 2 = 2ах, а также других конических сечений.

На протяжении многих веков три знаменитые задачи древности привлекали внимание выдающихся математиков. В процессе их решения рождались и совершенствовались многие математические методы.

В этой задаче требуется построить циркулем и линейкой куб вдвое большего объёма, чем заданный. Ребро искомого куба равно а , где а - ребро исходного куба. Если принять, что а = 1, то искомое ребро х есть корень уравнения x 3 - 2 = 0. У данного уравнения нет рациональных, а значит, и квадратично-ирациональных корней. Следовательно, удвоение куба нельзя осуществить циркулем и линейкой. Примерно такое расуждение было применено в начале XIX в., когда был подготовлен необходимый для этого алгебраический аппарат.

Считают, что задача об удвоении куба появилась во времена пифагорейцев, около 540 г. до н. э. Возможно, она возникла из задачи об удвоении квадрата, которую легко решить, опираясь на теорему Пифагора, — надо построить квадрат на диагонали данного квадрата. Согласно легенде, жители Афин, на которых боги ниспослали эпидемию чумы, отправили делегацию к оракулу на остров Делос за советом, как задобрить богов и избавиться от морового поветрия. Ответ был таков:

Известна и другая легенда. Греческий комментатор VI в. до н. э. сообщает о письме, предположительно написанном царю Птолемею I. В нём говорится, что царь Минос построил на могиле сына надгробие кубической формы, но остался недоволен размерами памятника и приказал удвоить его, увеличив вдвое ребро куба. Комментатор указывает на ошибку царя Миноса (площадь поверхности памятника в результате увеличилась в четыре, а объём — в восемь раз) и рассказывает, что тогда геометры попытались решить эту задачу.

a : x =x : y = y : b

(при b=2a получаем x=a ). Эту идею удалось реализовать Платону около 340 г. до н. э. с помощью нетрадиционных чертёжных инструментов — двух прямых углов (рис. 1).

Менехм примерно в .350 г. до н. э. решал задачу об удвоении куба, используя конические сечения — кривые, по которым плоскости пересекают конус. Свои решения дали также крупнейшие древнегреческие математики Евдокс, Эратосфен, Аполлоний, Герон, Папп и др.

Одно из решений задачи об удвоении куба показано на рис. 2. Здесъ BC=BD, AB=AC=EF, а прямая l = CE параллельна АD. Полагая ВС = a, АВ = b/2, АЕ = x и СF =у, можно найти, что x и y — два средних пропорциональных а и b или что

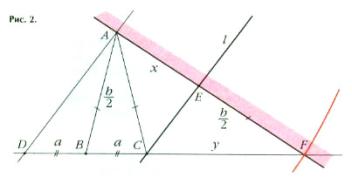
, а

в частности, x=a при b = 2а. Все точки и линии на этой фигуре, кроме прямой АЕF, строятся циркулем и линейкой; а прямую можно провести, если разрешить метки на линейке. Хватит двух меток Е и F; их нужно сделать на расстоянии b/2 друг от друга. Тогда прямую АЕF строят, поместив линейку так, чтобы её край проходил через A, одна метка попала на l , а другая на прямую ВС.

Несложно разделить любой угол с помощью циркуля и линейки на две, а некоторые углы — и на три равные части. Последняя операция называется трисекцией угла. Например, мы можем построить треть прямого угла, поделив пополам угол правильного треугольника, а проведя биссектрису в образовавшемся угле в 30°, получим угол величиной 15° — треть угла в 45°. Есть и другие углы, для которых трисекция выполнима. Наверное, подобные построения и вселили надежду открыть способ трисекции любого угла посредством циркуля и линейки. Эту задачу пытались решить ещё в V в. до н. э. в Греции.

На рис. 3 А0В — заданный угол, из точки В проведены прямая p = ВС, перпендикулярная ОА, и прямая l , параллельная ОА. Если теперь начертить прямую а = ОРQ так, чтобы её отрезок РQ, заключённый между р и l , равнялся 20В, то угол РОС составит треть данного угла. (Это можно доказать, пользуясь тем, что треугольники ОBD и ВDQ, где О — середина РQ, равнобедренные, и теоремой о внешнем угле треугольника.) Построить прямую а можно с помощью меченой линейки, т. е. линейки, на которой нанесены две метки на расстоянии 20В друг от друга.

Никомед с той же целью чертил свою конхоиду с полюсом О, основанием p и интервалом 20В; она пересекает l в искомой точке О.

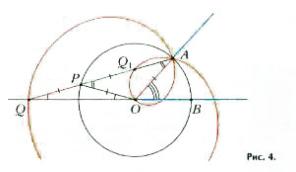
Архимед придумал свой способ трисекции. На данный угол — это угол AОВ между радиусами окружности. С помощью меченой линейки проведём прямую через точку А так, чтобы её отрезок РQ между окружностью и продолжением прямой ВО равнялся радиусу окружности. Как и на рис. 3, здесь образуются равнобедренные треугольники ОАР и ОРQ, и легко доказать, что угол ОQA втрое меньше данного.

Гиппий Элидский (около 420 г. до н. э.) для трисекции угла использовал кривую, впоследствии названную квадратрисой Динострата, который позже использовал её для решения квадратуры круга.

Квадратриса получается следующим образом. Пусть дана окружность радиуса а . Начнем вращать радиус ОА с угловой скоростью p /2 вокруг точки О - центра окружностии одновременно равномерно перемещать влево со скоростью а вертикальную прямую от точки А к точке С. Точка М их пересечения и будет описывать квадратрису. Если взять за оси координат прямую ОА и прямую 0В, то в момент времени t точка М будет иметь координаты

При стремлении t к 1 точка М стремится, к точке Р, при этом абсцисса точки М стремится к нулю, а у ординаты один множитель стремится к нулю, а другой - к бесконечности. Их произведение будет стремиться к числу 2а/ p , поэтому длина отрезка ОР равна 2a/p. Следовательно, имеет место соотношение АС/ОР= p .

Пусть теперь дана окружность радиуса г. Тогда имеем соотношение 2 p r /2r = АС/ОР, в котором известны АС, ОР и 2r-диаметр данной окружности. По ним мы можем построить отрезок, равный 2r- длине окружности, это будет четвертый пропорциональный отрезок к известным трем.

Французский математик П. Ванцель в 1837 г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой. Пусть b = a/3. По известной формуле, соs a = = 4 соs 3 b - 3 соs b. Тогда для величины х = 2 сов b получается уравнение x 3 – 3x - а = 0, где а = 2 соs a . Геометрическая задача трисекции данного угла а циркулем и линейкой разрешима тогда и только тогда, когда полученное алгебраическое уравнение разрешимо в квадратных радикалах. Возьмём, например, a = 60°. Тогда уравнение примет вид х 3 – 3x - 1 = 0. Оно неразрешимо в квадратных радикалах, а потому и трисекция с помощью циркуля и линейки в данном случае невозможна. Тем более она невозможна в общем случае. Интересно, что вообще для углов вида Зб0°/ n с целым п трисекцию удаётся осуществить тогда и только тогда, когда n не делится на 3.

В задаче о квадратуре круга требуется построить циркулем и линейкой квадрат, равновеликий данному кругу. Вероятно, задача была известна уже за две тысячи лет до н. э. в Древнем Египте и Вавилоне. Но первая прямая ссылка на неё относится к V в. до н. э. По свидетельству древнегреческого историка Плутарха, философ Анаксагор, коротая время в тюрьме, пытался квадрировать круг, т. е. превратить его в равновеликий квадрат. Если считать радиус данного круга равным 1, то сторона искомого квадрата должна составить .

Итак, задача о квадратуре круга оказалась наиболее сложной из трёх. Метод, использованный в двух других задачах, здесь не подошёл, так как число p имеет совершенно другую природу, чем или корни уравнений, к которым сводится трисекция. Только в 1882 г. Фердинанд Линдеман доказал, что число p трансцендентно, т. е. не является корнем никакого многочлена с целыми коэффициентами. Значит, оно и не квадратично-иррационально, поскольку в противном случае было бы корнем какого-либо многочлена. Так Линдеман наконец поставил точку в проблеме разрешимости посредством циркуля и линейки последней из трёх классических задач древности.

Читайте также:

  
• Физиология человека от античной эпохи до современности реферат
  
• Реферат горьковская железная дорога
  
• Реферат на тему лошадиная сила
  
• Гипертонический криз реферат медсестры
  
• Коменский основоположник педагогической науки реферат