Задачи о разладке реферат

Обновлено: 05.07.2024

Задачи наилучшего выбора с разладкой ( реферат , курсовая , диплом , контрольная )

Содержание

• 1. Байесовская модель задачи наилучшего выбора с разладкой
  • 1. 1. Постановка задачи
  • 1. 2. Байесовская модель наилучшего выбора с дисконтированием выигрыша
  • 1. 3. Байесовская модель наилучшего выбора с платой за наблюдения

  Актуальность темы

  При построении моделей в области биологии, менеджмента, социологии и других наук часто возникают задачи наилучшего выбора. Эти задачи отражают важные особенности реальных процессов принятия решений в условиях неопределенности. Поэтому актуальным является как рассмотрение новых постановок задач, так и разработка прикладных моделей на их основе. На практике также нередки ситуации, когда в процессе наблюдения вероятностный закон распределения характеристик случайного процесса изменяется, что влечет дополнительные трудности при принятии решений.

  Задача наилучшего выбора. Важным направлением в теории вероятностей являются задачи оптимального управления случайными процессами. Наряду с традиционными вероятностно-статистическими задачами в середине XX века началось систематическое исследование задач, которые теперь относят к вероятностной теории оптимального управления. Одним из разделов этой теории является теория оптимальных правил остановки в задачах наилучшего выбора.

  Проблемы наилучшего выбора впервые были представлены в 40-х годах в работах известного американского статистика А. Вальда в связи с задачами последовательного различения гипотез [3]. Основная особенность этих задач состоит в том, что наблюдатель последовательно обозревает независимые одинаково распределенные случайные величины с неизвестным законом распределения, и целью является определение типа распределения этих наблюдений. В отличие от классических методов ма тематической статистики, в которых число производимых наблюдений фиксируется заранее, методы последовательного анализа характеризуются тем, что момент прекращения наблюден ий (момент остановки) является случайным и определяется наблюдателем в зависимости от значений наблюдаемых случайных величин. Преимущество последовательных методов было продемонстрировано А. Вальдом на задаче различения двух простых гипотез по результатам независимых наблюдений. При этом было установлено, что подобные методы требуют в среднем меньшего числа наблюдений по сравнению с любым другим способом различения с фиксированным объемом выборки при тех же вероятностях ошибочных решений. Более того, А. Вальд указал и тот последовательный метод (названный критерием последовательных отношений вероятностей), который является оптимальным в классе всех последовательных методов [28].

  • выбор осуществляется в несколько этапов, то есть растянут во времени;

  • на процесс выбора наложены стратегические и информационные огранычения, связанные с полной или частичной недоступностью для выбора пропущенных вариантов и статистической неопределенностью качества будущих объектов;

  • эффект выбора (выигрыш) тем выше, чем лучше выбранные варианты.

  Описанная задача была решена в 1961 г. независимо друг от друга Е. Б. Дынкиным (основываясь на теории марковских процессов [7]) и Д. Линдли (с помощью метода динамического программирования [61]). Оба решения приводят к неожиданному и красивому результату. Оказывается, необходимо пропустить (запоминая относительные ранги) примерно треть всех претендентов (п/е), а затем из оставшихся принять соискателя, который окажется лучше всех просмотренных ранее. При этом вероятность удачного выбора при п —" оо равна 1/е.

  Эвристическое решение этой задачи было впервые представлено в работе [50], а в статье [34] дано строгое доказательство полученного результата. Оптимальным правилом остановки является многопороговая стратегия — на каждом шаге / (1 с^ (уравнение для вычисления значений оптимальных порогов можно найти, например, в [50]). Вероятность успешного выбора при большом числе наблюдений равна примерно 0.58. Различные постановки задач наилучшего выбора с полной информацией были рассмотрены авторами работ [36, 51, 52, 58, 68, 73, 74, 75] и другими.

  Помимо четко разграниченных подклассов задач с полной и с отсутствием информации, рассматривают также задачи с различными ограничениями на доступную информацию о наблюдениях — задачи с частичной информацией, в которых, например, известен закон распределения, но неизвестны его параметры, либо неизвестны точные значения наблюдаемых случайных величин и т. д. (см., например, [70, 71, 72]).

  Для каждого из подклассов было рассмотрено большое количество различных постановок задач наилучшего выбора. Интерес к этим задачам обусловлен следующими причинами. Во-первых, задачи наилучшего выбора отражают существенные особенности реальных процессов выбора в условиях неопределенностиво-вторых, они всегда имеют содержательную постановку и легко интерпретируемые решения в экологии, информационных технологиях, экономике и других науках (см. [13, 15, 77]).

  Модели, связанные с обнаружением разладки, применяются, например, при статистическом анализе историчесЕсих текстов и установлении авторства [2], контроле качества технологических операций [26] и т. д.

  Задача наилучшего выбора с разладкой. В данной диссертационной работе проводится исследование проблем, принадлежащих классу задач наилучшего выбора с разладкой. Этот класс составляют задачи, в которых необходимо осуществить наилучший выбор в условиях ожидаемого изменения характеристик базового случайного процесса.

  Момент разладки 9 имеет геометрическое распределение с параметром, а (0 1, а перед генерацией каждой новой случайной величины состояние системы изменяется согласно следующей матрице переходов: а 1 — а.

  Наблюдателю известны функции распределения случайных величин в состояниях ?>1 и и т. д.

  В диссертационном исследовании рассматриваются два класса стратегий наблюдателя: однопороговые и многопороговые стратегии. Многопороговая стратегия — это такая стратегия, при которой наблюдатель на каждом шаге г (г = 1, ., п) устанавливает порог отвергая ее в противном случае. Однопорого-вая стратегия — это такая многопороговая стратегия, при которой ^ = д,.

  Впервые вариант задачи наилучшего выбора с разладкой был рассмотрен в работе [78], где в условиях модели (А) необходимо максимизировать ожидаемое принятое значение из последовательности случайных величин. При этом наблюдатель оценивает вероятность нахождения системы в одном из состояний, на основе чего модифицирует значения порогов.

  Представленная диссертационная работа посвящена исследованию задач наилучшего выбора с разладкой, комбинирующих в себе основные особенности и классических проблем наилучшего выбора, и задач обнаружения разладки. Актуальность диссертационной работы подтверждает большое внимание, которое уделяется этим задачам при проведении как теоретических изысканий, так и внедрении математических моделей в технологические процессы.

  Цель диссертационной работы заключается в построении решений задач наилучшего выбора с разладкой методами теории оптимальной остановки и некооперативной теории игр.

  В работе исследуются следующие основные задачи:

  Заключение

  В работе представлены результаты исследования задач наилучшего выбора с полной информацией с разладкой.

  Рассмотрена задача максимизации вероятности выбора наилучшего значения из последовательности случайных величин в условиях ожидаемой разладки. Получен аналитический вид формулы, определяющей оптимальное значение порога в зависимости от значений параметров задачи. Представлены результаты численного моделирования, которые демонстрируют характерные особенности задачи, связанные с выбором наблюдения до или после разладки. Рассмотрен случай большого числа наблюдений.

  Исследована теоретико-игровая задача оптимальной остановки для т лиц. Рассмотрены три постановки задачи, отличающиеся параметром равномерного распределения наблюдаемых случайных величин. С помощью метода динамического программирования получены оптимальные пороги. Представлено обобщение модели на случай разладки. Проведено численное моделирование значений оптимальных порогов принятия наблюдений.

  Рассмотрена многопороговая задача наилучшего выбора с полной информацией с разладкойцелью наблюдателя является максимизация ожидаемого значения принятой случайной величины с помощью многопороговой стратегии. Исследованы два варианта, изменения в результате разладки параметра равномерного распределения наблюдаемых случайных величин. Представлены результаты численного моделирования значений оптимальных порогов.

  Рассмотрены две игровые постановки задачи наилучшего выбора с разладкой, в которых целью наблюдателей является максимизация ожидаемого значения принятой случайной величины. Для каждой из постановок построены функции выигрыша и найдены оптимальные однопороговые стратегиирассмотрен частный случай абсолютного приоритета одного из игроков и вариант большого числа наблюдений.

  Рассмотрена байесовская модель задачи наилучшего выбора с разладкой, в которой наблюдатель имеет неполную информацию о наблюдаемых случайных величинах. Исследованы модели с дисконтированием и платой за наблюдения. Предложена байесовская стратегия порогового вида, в которой на каждом шаге учитывается апостериорная оценка вероятности разладки системы. Представлены результаты численного моделирования, на основании которых можно сделать вывод, что указанная стратегия дает больший выигрыш, чем использование однопороговых стратегий, не учитывающих поступающую информацию. На основе байесовской модели задачи наилучшего выбора с разладкой описана модель распределения вычислительных ресурсов в высокопроизводительных системах.

  
  

  ДОКЛАДЫ АКАДЕМИИ НАУК, 2013, том 450, № 2, с. 135-139

  ЗАДАЧА О НЕПРЕРЫВНОЙ РАЗЛАДКЕ ВИНЕРОВСКОГО ПРОЦЕССА

  © 2013 г. А. Ф. Алиев

  Представлено академиком А.Н. Ширяевым 07.11.2012 г. Поступило 13.11.2012 г.

  Для более наглядного перехода к этой постановке переформулируем классическую байесовскую задачу о разладке Ширяева [9, гл. 6, п. 2]. Пусть 0, = |/

  и порождает фильтрацию (9,), > 0, т.е. 9, = ст(У„ з |>&

  Как видно, мы переформулировали задачу в терминах "процесса разладки" (0,), > 0, хотя в классической задаче этот процесс и является тривиальным пуас-соновским скачком. Наш интерес состоит в изучении процессов 0 более сложной структуры, и в данной работе мы рассмотрим частный случай, при котором 0, = 0О + ст2В,, где (Щ, В) — винеровская пара с (В, Щ>, = р 1, а случайная величина 0О ~ Я(ш, р). Это простейшая модель, отвечающая непрерывной разладке наблюдаемого процесса, и мы будем рассматривать ту же функцию риска (3), где | — произвольная константа. Таким образом, мы минимизируем комбинацию вероятности ложной тревоги и времени, которое частица проводит в "критическом" состоянии.

  Для решения этой задачи сведем ее в первую очередь к задаче оптимальной остановки. Для этого стандартными преобразованиями (см. [4]) приведем (3) к эквивалентной форме

  что мы перепишем в более наглядной для наших целей форме

  где п, = Р(0 , > ||9,). Нахождение динамики процесса (п ,), > 0 сводится к нахождению условного распределения 0 , по сигма-алгебре 9,, что, в свою очередь, подробно изучает теория (линейной) фильтрации. Действительно, наш случай представляет собой не что иное, как классический фильтр Калма-на в непрерывном времени. Как хорошо известно из общей теории [2, 7], Law(0 ,|9,) есть нормальное

  распределение Я( 0,, р,) с параметрами, подчиняющимися дифференциальным уравнениям

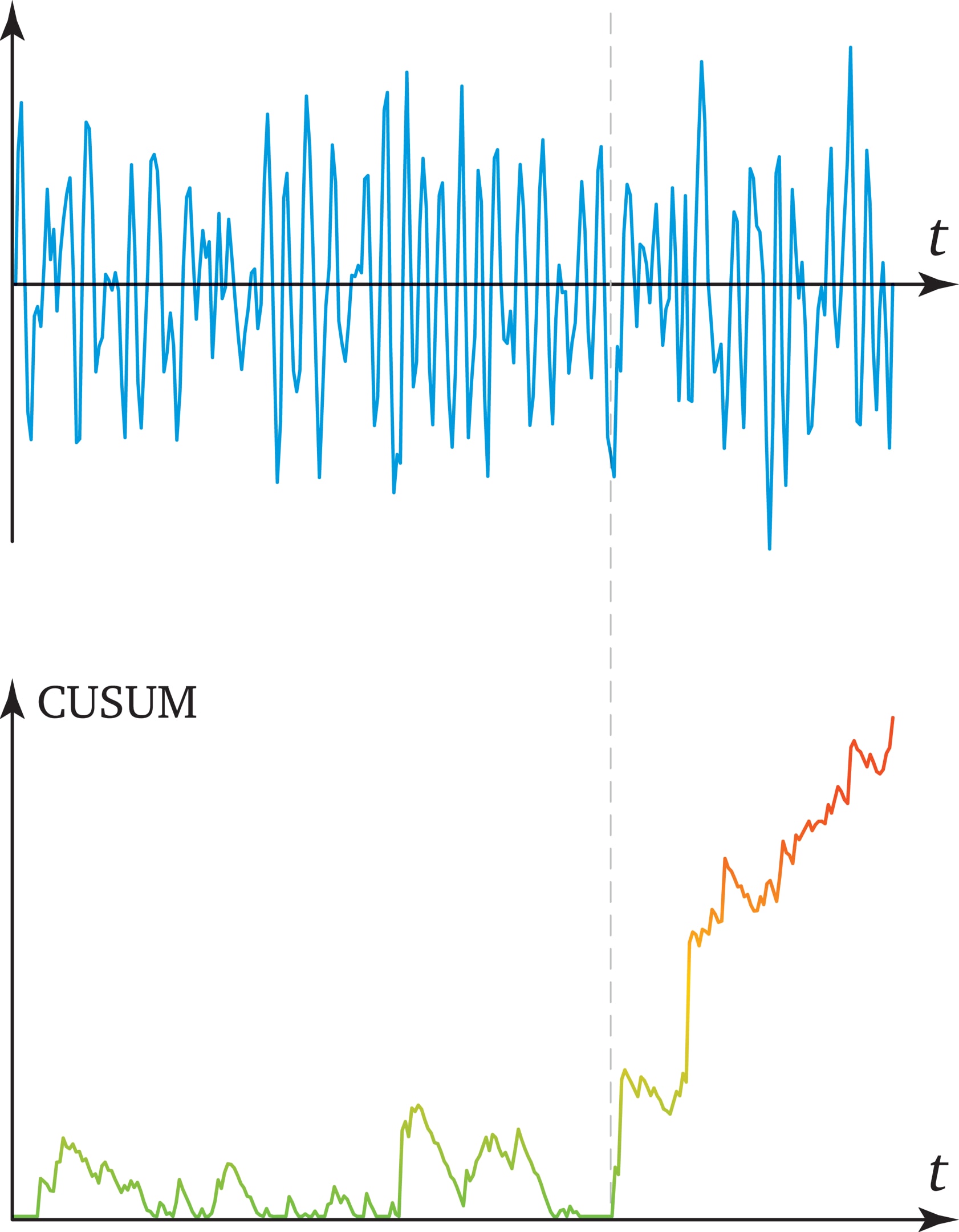
  Так устро­ена при­рода, что многие реаль­ные процессы являются слу­чай­ными, наблю­да­телю неиз­вестно будущее. Oдна из задач тео­рии при­ня­тия реше­ний в усло­виях неопре­де­лён­но­сти — опре­де­ле­ние в реаль­ном времени момента раз­ладки: момента, когда про­ис­хо­дит скач­ко­об­раз­ное изме­не­ние харак­те­ри­стик процесса. Раз­ладка — событие ред­кое, но суще­ствен­ное, и её свое­времен­ное обна­руже­ние при ана­лизе дан­ных часто имеет решающее зна­че­ние.

  
  

  Это можно ощу­тить, почув­ство­вать на сле­дующих при­ме­рах из раз­ных обла­стей. Наблю­де­ние и ана­лиз при­род­ных явле­ний — метео­ро­логия, пред­ска­за­ние зем­ле­тря­се­ний на основе ана­лиза пока­за­те­лей дат­чи­ков сейсми­че­ских станций. В эко­номике — ана­лиз финан­со­вых рын­ков и кон­троль каче­ства выпус­ка­емой про­дукции. В компью­тер­ных системах — мони­то­ринг динами­че­ских фак­то­ров, харак­те­ри­зующих изме­не­ния системы, в част­но­сти, для обна­руже­ния неже­ла­тель­ных вторже­ний. Отдель­ная чув­стви­тель­ная область — медицина: слеже­ние за сиг­на­лами жиз­не­де­я­тель­но­сти боль­ного в палате интен­сив­ной терапии, обна­руже­ние эпи­демий.

  Форму­ли­ровка задачи обна­руже­ния раз­ладки в веро­ят­ност­ных терми­нах свя­зана со слу­чай­но­стью зна­че­ний наблю­да­емых дан­ных. Опи­сать их раз­но­об­раз­ный харак­тер как-то про­сто вряд ли возможно, поэтому и при­ме­ня­ется веро­ят­ност­ное опи­са­ние, учи­ты­вающее, что эти вели­чины — слу­чай­ные, их зна­че­ния меняются от одного момента времени к другому.

  Методы реше­ния задач ско­рейшего обна­руже­ния в зна­чи­тель­ной мере опи­раются на современ­ный аппа­рат тео­рии слу­чай­ных процес­сов, сто­ха­сти­че­ского исчис­ле­ния, тео­рии мар­тинга­лов, нели­ней­ной фильтрации и т. д. В свою оче­редь, многие из этих раз­де­лов полу­чили раз­ви­тие именно на пути реше­ния задач ско­рейшего обна­руже­ния. Это служит хорошей иллю­страцией того, как про­ис­хо­дит раз­ви­тие тео­рии, когда она наце­лена на реше­ние кон­крет­ных задач, имеющих прак­ти­че­ский инте­рес. В общем-то, и всё раз­ви­тие веро­ят­ност­ных дис­ци­плин имеет сход­ный харак­тер. Из исто­рии науки известно, что зарож­де­ние тео­рии веро­ят­но­стей было свя­зано с оцен­кой благопри­ят­ных исхо­дов в азарт­ных играх, а нача­лом матема­ти­че­ской ста­ти­стики стали попытки раз­реше­ния вопро­сов гео­де­зии и аст­ро­номии.

  Мы при­во­дим эти слова, чтобы под­черк­нуть: поста­новки задач и извест­ные методы их реше­ния должны побуж­дать чита­теля форму­ли­ро­вать новые задачи, искать для их реше­ния новые под­ходы, стиму­ли­рующие раз­ви­тие и соб­ственно тео­ре­ти­че­ских иссле­до­ва­ний.

  Пример наблюдаемости системы в нашей жизни

  Экскурс в историю

  
  

  Система становится не только непредсказуемой, но и неуправляемой. Тогда надо как можно быстрее выявить и устранить источник внешнего вмешательства и вернуть ее в управляемое состояние. Дело за малым. Нужно научиться различать состояния, в которых находится система, а затем решать, что и кому надо с ней делать (или не делать).

  Карты Шухарта как раз и отвечают на вопрос: надо или не надо вмешиваться в систему? И если надо, то кому и каким образом?

  Как работают методы обнаружения разладки?

  Мы уже упомянули, что все, происходящее вокруг нас можно описать некоторым случайным процессом (его еще называют вероятностным или стохастическим). Течение этого процесса может быть различным, в зависимости от случая, а также для него определена вероятность того или иного его течения. Множество случайных явлений, которые существуют в природе, являются функциями времени. В заданный момент времени величина случайного процесса является случайной величиной. Таким образом, случайный процесс можно рассматривать как случайную величину, индексируемую неким параметром.

  Какие бывают методы обнаружения разладки?

  При обнаружении обоих методов также появляются две возможные ошибки:

  - Ложная тревога, когда решение о наличии разладки принимается в ее отсутствие.

  - Ситуация, когда разладка есть, а мы считаем, что ее нет.

  Основные характеристики последовательных методов обнаружения разладки случайных процессов — это среднее время между соседними ложными тревогами и среднее время запаздывания при обнаружении разладки. Совершенствование методов обнаружения разладки как раз идет по двум направлениям — либо уменьшать количество ложных срабатываний, либо уменьшать количество моментов, когда мы пропускаем важные изменения системы.

  Достаточно хорошо изученной к настоящему времени является задача обнаружения изменения распределения в последовательности случайных величин. Для решения этой задачи применяются методы скользящего среднего, экспоненциального сглаживания, кумулятивных сумм. К настоящему времени разработан также ряд методов обнаружения моментов разладки случайных процессов с зависимыми значениями. Часто в качестве моделей наблюдаемых процессов используются процессы авторегрессионного типа, которые позволяют при небольшом числе параметров хорошо аппроксимировать корреляционную функцию. Во многих случаях задача обнаружения момента разладки случайных процессов оказывается тесно связанной с задачей оценивания параметров этих процессов. Для оценивания неизвестных параметров процессов авторегрессионного типа применяются методы наименьших квадратов, максимального правдоподобия, стохастической аппроксимации. Свойства получаемых оценок изучаются в асимптотике, при неограниченном увеличении объема наблюдений. Это позволяет установить скорость сходимости оценок к истинным значениям параметров, а также найти предельное асимптотическое распределение оценок.

  Наши кейсы

  О том, как мы использовали карты Шухарта, чтобы определить эффективность интернет-тролля на новостном портале, можно почитать здесь.

  О том, как с помощью карт Шухарта студенты смогли в 10 000 раз сократить количество ошибок в новой версии системы по сравнению со старой, написанной опытными программистами, читайте тут.

  О том, как с помощью карт Шухарта увидеть, как повсеместно обманывают менеджеров по продажам — узнаете, читая блог. Материал в разработке и скоро появятся.

  
  

  Устинов Филипп Александрович. Задача о разладке для процессов Леви в обобщенной байесовской постановке : диссертация . кандидата физико-математических наук : 01.01.05 / Устинов Филипп Александрович; [Место защиты: Моск. гос. ун-т им. М.В. Ломоносова. Мех.-мат. фак.].- Москва, 2009.- 76 с.: ил. РГБ ОД, 61 10-1/105

  Введение к работе

  В настоящей работе рассматривается задача о разладке в обобщенной байесовской постановке для процессов Леви. Задача о разладке состоит в скорейшем обнаружении изменения вероятностных характеристик процесса (в данном случае триплета характеристик). Впервые проблема скорейшего обнаружения изменения сноса винеровского процесса была поставлена в докладе А.Н. Колмогорова и А.Н. Ширяева на VI совещании по теории вероятностей и математической статистике (Вильнюс, 5-Ю сентября 1960 г). Представленные в этом докладе новые подходы получили развитие в работах А.Н. Ширяева 1 ' 2 ' 3 .

  Некоторые частные случаи пуассоновской задачи о разладке были рассмотрены в работах 4,5 . Пешкир и Ширяев представили полное решение этой задачи (в байесовской постановке) 6 . Заметим, что пуассоновская задача заметно отличается от винеровской по методам исследования.

  Дальнейшая деятельность развивалась в нескольких направлениях. Одно из них - поиск классов процессов, допускающих решение при помощи тщательного анализа возникающих уравнений. В этом направлении Гапеев нашел специальный случай, когда пуассоновская задача с экспоненциальными скачками допускает аналитическое изучение 7 (см. также 8 ).

  В работах 9,10 рассматриваются задачи о разладке для составного пуас-соновского процесса и для многомерного процесса, координаты которого

  'Ширяев А.Н. Обнаружение спонтанно возникающих эффектов // Докл. АН СССР. 1961. Т. 138, вып. 4. С. 799-801.

  2 Ширяев А.Н. Задача скорейшего обнаружения нарушения стационарного режима // Докл. АН СССР. 1961. Т. 138, вып. 5. С. 1039-1042.

  3 Ширяев А.Н. Об оптимальных методах в задачах скорейшего обнаружения // Теория вероятностей и ее применения. 1963. Т. VIII, вып. 1. С. 26-51.

  4 Davis, М. Н. А. (1976). A note on the Poisson disorder problem. Banach Center Publ. 1 65-72.

  5 Galchuk, L. I. and Rozovskii, B. L. (1971). The disorder problem for a Poisson process. Theory Probab. Appl. 16 712-716.

  6 Peskir, G. and Shiryaev, A. N. (2002). Solving the Poisson disorder problem. In Advances in Finance and Stochastics. Essays in Honour of Dieter Sondermann (K. Sandmann and P. Schunbucher, eds.) 295-312. Springer, Berlin.

  7 Pavel V. Gapeev, The disorder problem for compound Poisson processes with exponential jumps, Ann. Appl. Probab. 15 (2005), no. 1A, 487-499.

  8 E. Bayraktar and S. Sezer. Quickest detection for a Poisson process with a phase - type changetime distribution. Technical report, University of Michigan, 2006.

  'Dayanik, S. and Sezer, S. O. (2006). Compound Poisson disorder problem. Math. Oper. Res. 31, 4, 649-672.

  10 Savas Dayanik, H. Vincent Poor and Semih O. Sezer (2006). Multisource Bayesian Sequential Change Detecion, Annals of Applied Probability, 18:2, 552-590.

  и(х) = inf Е* I Tbs ds

  К ' тєМт- J

  появляется в правой части следующей задачи - рассматриваемой до второго прыжка и т.д. Этот метод применим только для процессов с конечным числом скачков на конечном временном интервале.

  В работе 11 впервые вводится обобщенный байесовский подход для ви-неровской задачи о разладке. Представлено решение этой задаче о разладке. Также получена асимптотика функции риска. Решение обобщенной байесовской задачи о разладки для некоторого пуассоновского процесса и сходимость к винеровскому случаю (при частотах скачков, стремящихся к бесконечности) рассмотрено в работе 12 .

  В последние десятилетия резко возросла потребность в решении практических задач, требующих быстрого обнаружения разладки в той или иной форме. Важные применения задачи о разладке - сейсмология, скорейшее обнаружение сбоев промышленного оборудования (во время контроля качества), изменение рискованности различных финансовых инструментов, раннее обнаружение начала эпидемий, военные применения, радиолокация, охрана ценных ресурсов, обеспечение безопасности сложных технических систем (самолетов, судов, космических кораблей, ядерных электростанций, компьютерных сетей). В последнее время проявляется значительный интерес к задачам о разладке в связи с такими явлениями, как биотерроризм, компьютерные атаки.

  Многие практические задачи можно описать как поток некоторых событий или данных (запросов, сбоев, цен и т.п.). Соответственно, естественно моделировать эти потоки с помощью случайных процессов или цепей. Во многих из этих задач данные собираются разнородные или

  1 Weinberg, Е.А. and Shiryaev, A.N. (2006). Quickest detection of drift change for Brownian motion in generalized Bayesian and minimax settings, Statistics and Decisions 24, Issue 4, 445-470.

  12 E. V. Burnaev, Disorder problem for a Poisson process in the generalized Bayesian setting, UMN, 20O7, 62:4(376), 151-152.

  из нескольких источников, чтобы обнаружить сбой как молено раньше. К примеру, можно следить за непрерывно меняющимся уровнем масла, температурой, давлением, и периодически измерять число и тип частиц-примесей (см. 13 ). Поэтому полезно рассматривать наряду с непрерывной составляющей разнораспределенные скачки. Во многих моделях естественным оказывается рассматривать процессы с независимыми приращениями.

  Многочисленны применения в финансовой математике - к примеру, для расчета финансовых рисков контрактов на поставки электроэнергии используются модели с диффузиями с прыжками (см. 14,15 ). Тарта-ковский А.Г., Розовский Б.Л. и др. применили теоретические методы для обеспечения безопасности сетей; Basseville М., Benveniste А., Никифоров И.В. и другие использовали их для разработки эффективных алгоритмов обнаружения неисправностей в сложных технических устройствах и т.п. В последнее время все большую популярность приобретают модели с процессами Леви, являющиеся естественным обобщением моделей, основанных на винеровском и пуассоновском процессах.

  Заметим, что в будущем потребность в решении задач быстрого обнаружения разладки будет только возрастать. Это связано с технологическим и экономическим развитием, а также с сопутствующим ростом ущерба экологии. С развитием инфраструктуры и возникновением все большего числа сложных технических объектов возрастают риски различных техногенных катастроф, соответственно возрастает необходимость точного учета и управление этими рисками. В связи с этим ожидается дальнейшее развитие математических моделей задач о разладке в направлении усложнения. Можно предвидеть введение неклассических постановок (других способов оценки риска) и расширение рассматриваемых классов процессов.

  В настоящей работе получены обобщения части результатов работ 11,12 - они распространены на процессы Леви. Найден оптимальный момент остановки. Задача о разладке изучается в обобщенной байесовской постановке.

  В классической байесовской постановке считается известным распре-

  13 Byington, С. S. and Garga, А. К. (2001). Handbook of Multisensor Data Fusion. Press, Chapter Data fusion for developing predictive diagnostics for electromechanical systems.

  14 Weron, R., Bierbrauer, M., and Truck, S. (2004). Modeling electricity prices: jump diffusion and regime switching. Physica A Statistical Mechanics and its Applications 336, 39-48.

  15 Cartea, I. and Figueroa, M. (2005). Pricing in electricity markets: A mean reverting jump diffusion model with seasonality. Applied Mathematical Finance 12, 4 (December), 313-335.

  деление момента сбоя. В приложениях зачастую удобнее использовать постановку задачи, в которой момент разладки представляет собой детерминированный неизвестный параметр.

  В данной работе также получены асимптотические оценки для функции риска. Они, в частности, оказываются полезными оценками в задаче о разладке в минимаксной постановке, при поиске асимптотически оптимальных правил остановки. Минимаксная постановка весьма естественна как с практической, так и с теоретической точки зрения, но ее точное решение пока неизвестно.

  Итак, в настоящей работе проводится развитие современных теоретических моделей. Таким образом, ее тематика является актуальной как с точки зрения развития теории, так и с точки зрения практических применений.

  Цель работы

  Целью данной работы является развитие теории задач о разладке в направлении расширения изучаемых классов процессов и способов оценки риска. В соответствии с этой целью, были поставлены следующие задачи исследования:

  Исследовать задачу о разладке для процессов Леви в случае, когда момент разладки является неизвестным детерминированным параметром, а среднее время запаздывания оценивается с помощью обобщенной байесовской функцией риска.

  Изучить асимптотическое поведение функции риска при стремлении к бесконечности среднего времени до ложной тревоги.

  Научная новизна

  Основные результаты диссертации являются новыми и состоят в следующем:

  Найден оптимальный момент в задаче о разладке для произвольных процессов Леви в обобщенной байесовской постановке.

  Установлена связь асимптотики функции риска при стремлении к бесконечности среднего времени до ложной тревоги в случае базисных процессов Леви со средним временем объявления тревоги.

  В некоторых случаях асимптотика из предыдущего пункта найдена в виде явной формулы.

  Методы исследования

  В работе применяются методы теории вероятностей, в частности методы теории случайных процессов и теории задач об оптимальной остановке марковских процессов, а также некоторые методы функциональною анализа.

  Теоретическая и практическая значимость

  Работа носит теоретический характер. Ее результаты и методы могут быть использованы в дальнейших исследованиях задач об оптимальной остановке. Развиты подходы, которые полезны для дальнейших обобщений, таких как рассмотрение минимаксной постановки задачи о разладке для процессов Леви, а также расширение на многомерный случай. Результаты работы также могут быть использованы при построении математических моделей реальных процессов с разладкой. Найденные асимптотические оценки также полезны (как для качественной оценки на практике, так и для новых теоретических построений).

  Апробация работы

  На Большом семинаре кафедры теории вероятностей МГУ им. М. В. Ломоносова (2008).

  Основные результаты диссертации опубликованы в 3 работах автора, 2 из которых - статьи в ведущих рецензируемых научных журналах. Список приведен в конце автореферата.

  Структура диссертации

  Диссертация состоит из введения, двух глав, включающих 12 параграфов, и списка литературы из 65 наименований. Общий объем диссертации составляет 76 страниц.

  2 Краткое содержание диссертации

  Во введении обоснована актуальность задачи скорейшего обнаружения, рассказано об истории развития теоретических подходов к решению этой задачи, приведен обзор современных работ по теории и применениям задачи о разладке. Также приведено краткое содержание диссертации. Далее приведены основные утверждения, доказанные в диссертации, по главам.

  Читайте также:

    
  • Рекреационные ресурсы австралии реферат
    
  • Титульный лист реферата мвд россии
    
  • Реферат на тему системы неравенств
    
  • Темы рефератов по истории алтайского края
    
  • Закон забывания эббингауза реферат