Вынужденные колебания под действием гармонической силы реферат

Обновлено: 05.07.2024

Вынужденные колебания под действием гармонической силы. Режимы медленных, быстрых и резонансных колебаний. Амплитудно-частотные и фазо-частотные характеристики. Баллистический режим колебаний. Установление колебаний. Характеристики различных колебательных систем. Параметрические колебания. Автоколебания.

В предыдущей лекции мы рассмотрели свободные затухающие колебания, возникающие при начальном кратковременном воздействии внешних сил на колебательную систему. Между тем, в повседневной практике мы сталкиваемся с незатухающими колебаниями, для поддержания которых необходимо подводить энергию к колебательной системе, чтобы компенсировать ее энергетические потери.

Одним из распространенных способов поддержания незатухающих колебаний является непрерывное воздействие на колеблющуюся массу периодической силы ( вынуждающей силы )

меняющейся во времени , вообще говоря, произвольно в пределах периода длительностью . Если, например, такую силу приложить к колеблющейся массе описанного выше пружинного маятника (рис. 2.1), то уравнение ее движения примет вид:

(2.2)

Рис. 2.1.

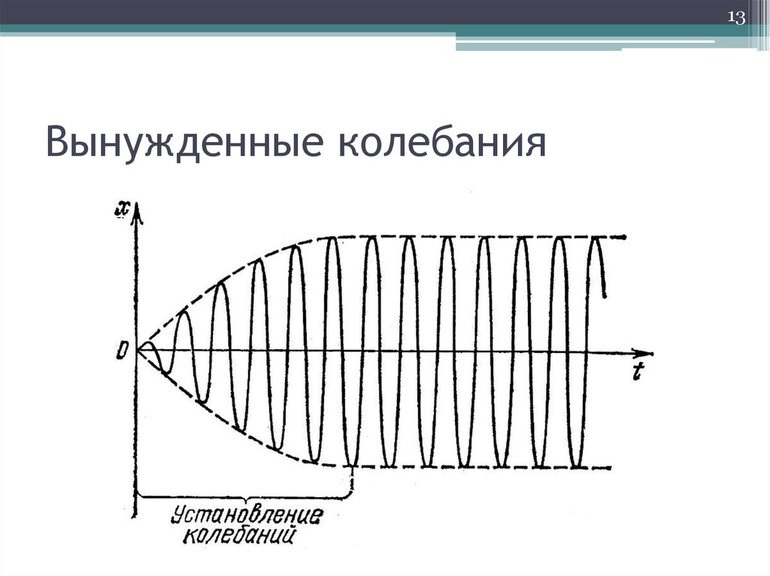
Опыт показывает, что если сила внезапно начинает действовать (например, в момент времени ), то маятник начнет постепенно раскачиваться, и спустя какое-то время его колебания установятся. По порядку величины время установления таких вынужденных колебаний будет совпадать с временем затухания Далее мы сконцентрируем внимание именно на установившихся колебаниях. Естественно, что параметры таких колебаний будут зависеть от конкретного вида силы Из математики хорошо известно, что любую периодическую функцию можно представить в виде ряда Фурье:

Физический смысл этого представления состоит в том, что периодическое воздействие эквивалентно одновременному воздействию постоянной силы и набора гармонических сил с соответствующими амплитудами начальными фазами и частотами кратными низшей (основной) частоте

Чтобы получить полную картину вынужденных колебаний под действием силы (2.3), необходимо принять во внимание линейность уравнения (2.2). Это позволяет представить его решение как сумму гармонических колебаний:

происходящих с установившимися амплитудами и фазами на частотах соответствующих гармоник вынуждающей силы (2.3). Каждое слагаемое в (2.4) может рассматриваться как вынужденное гармоническое колебание, происходящее под действием внешней гармонической силы с амплитудой и частотой

Амплитуды и фазы требуют определения, и мы перейдем сейчас к их нахождению.

Вынужденные колебания под действием гармонической силы.

Пусть внешняя сила меняется по гармоническому закону

Уравнение (2.2) в этом случае принимает вид:

Под действием этой силы маятник в установившемся режиме будет совершать гармонические колебания

Как показывает опыт, амплитуда и начальная фаза (т.е. сдвиг фазы между смещением и силой ) установившихся колебаний зависят не только от амплитуды силы (что очевидно из уравнения (2.6)), но и от того, насколько частота вынуждающей силы отличается от собственной частоты колебаний маятника Наиболее сильно маятник будет раскачиваться, когда эти частоты практически совпадают:

Прежде чем приступить к нахождению и заметим, что для механических колебательных систем не так просто с технической точки зрения осуществить воздействие гармонической силы непосредственно на движущуюся массу. Гораздо проще это сделать для электрических и оптических колебательных систем, например, для колебательного контура , подключенного к внешнему источнику переменного напряжения. Легко, однако, видеть, что можно поддерживать вынужденные колебания маятника, изображенного на рис. 2.1, иным способом, не прикладывая непосредственно внешнюю силу к массе Достаточно лишь эту силу приложить к левому концу свободной пружины так, чтобы этот конец двигался по гармоническому закону (рис. 2.2). Тогда удлинение пружины составит величину а сила упругости, приложенная к массе , будет равна Поэтому уравнение движения массы запишется в виде:

(2.8)

Рис. 2.2.

Если принять во внимание, что сила упругости пружины в отсутствие смещения груза (s = 0) равна

то уравнение (2.8) полностью эквивалентно уравнению (2.6). Сила (2.9) выполняет роль внешней гармонической силы в классической схеме, изображенной на рис. 2.1. Эта сила легко может быть визуализирована, поскольку ее величина и направление однозначно определяется смещением подвижного левого конца пружины. Это, в свою очередь, дает возможность наглядно продемонстрировать фазовые соотношения между силой (или смещением ) и смещением колеблющейся массы.

Перепишем уравнение (2.8) следующим образом:

Решение этого уравнения будем искать в виде гармонического колебания (2.7), где амплитуда и фаза могут быть определены, если подставить (2.7) в (2.10). Мы сделаем это несколько позднее, а пока рассмотрим три важных режима вынужденных колебаний.

Медленные колебания.

Если частота вынуждающей силы значительно меньше то скорость и ускорение колеблющейся массы будут очень малыми. Поэтому можно пренебречь первыми двумя членами в левой части уравнения (2.10) и записать его в приближенном виде:

Его решение очевидно:

В этом режиме смещение груза пропорционально внешней силе и не зависит от величины его массы . Решение (2.12) является, по существу, математическим выражением закона Гука для статической деформации пружины. Поэтому этот режим можно назвать квазистатическим (почти статическим). Амплитуда колебаний в соответствии с этим законом равна а смещение изменяется в фазе с внешней силой.

В схеме, изображенной на рис. 2.2, это эквивалентно тому, что смещение массы практически повторяет смещение левого конца пружины:

поскольку Это и не удивительно, т.к. для движения массы с пренебрежимо малым ускорением не требуется больших деформаций пружины:

Вынужденные колебания – это колебания, происходящие под действием внешней периодически действующей силы.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.

Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия.

Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д.

Резонанс

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы.

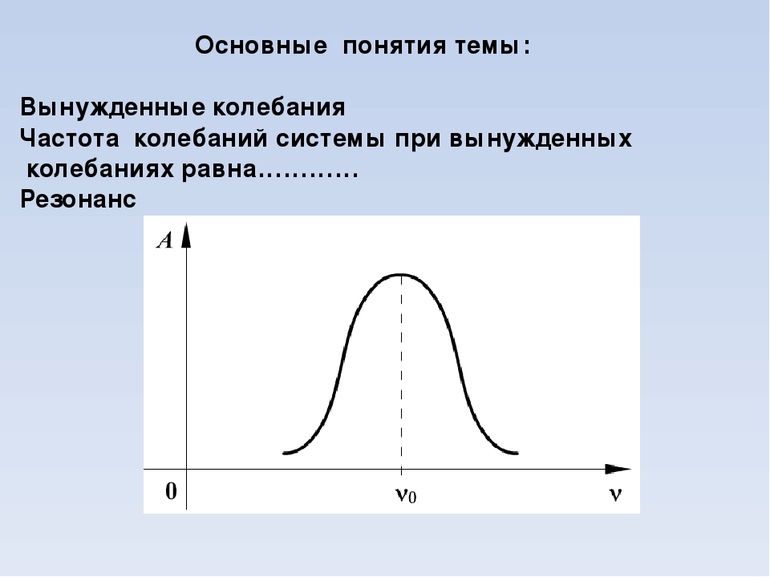
На рис.1 показана зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Видно, что эта амплитуда достигает максимума при определенном значении частоты, т.е. при _0" width="52" height="11" />
, где _0-" width="30" height="11" />
собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.

Рис.1. Резонансные кривые для различных значений силы трения.

С явлением резонанса мы часто встречаемся в повседневной жизни. Если в комнате задрожали стекла при прохождении по улице тяжелого грузовика, это значит, что собственная частота колебаний стекол равна частоте колебаний машины. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной.

Явление резонанса необходимо учитывать при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. Однако резонанс также может быть полезен. Явление резонанса используется при настройке радиоприемника на определенную частоту радиовещания, а также во многих других случаях.

Примеры решения задач

Задание	На конец пружины горизонтального маятника, груз которого имеет массу 1 кг, действует переменная сила, частота колебаний которой равна 16 Гц. Будет ли при этом наблюдаться резонанс, если жесткость пружины 400 Н/м.
Решение	Определим собственную частоту колебательной системы по формуле:

Гц

Так как частота внешней силы не равна собственной частоте системы, явление резонанса наблюдаться не будет.

Задание	Маленький шарик подвешен на нити длиной 1 м к потолку вагона. При какой скорости вагона шарик будет особенной сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 12,5 м.
Решение	Шарик совершает вынужденные колебания с частотой , равной частоте ударов колес о стыки рельсов:

Если размеры шарика малы по сравнению с длиной нити, то систему можно считать математическим маятником, собственная частота колебаний которого:

. Таким образом можно записать:

откуда скорость вагона:

Заметим, что если некоторая физическая величина принимает мнимые значения, то это означает какую-то необычность, экстраординарность соответствующего явления. В рассмотренном примере экстраординарность заключается в том, что процесс перестает быть периодическим. Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону… Читать ещё >

Вынужденные колебания. Резонанс ( реферат , курсовая , диплом , контрольная )

Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.

Предположим, что на материальную точку, кроме квазиупругой силы и силы трения, действует внешняя вынуждающая сила:

1 Заметим, что если некоторая физическая величина принимает мнимые значения, то это означает какую-то необычность, экстраординарность соответствующего явления. В рассмотренном примере экстраординарность заключается в том, что процесс перестает быть периодическим.

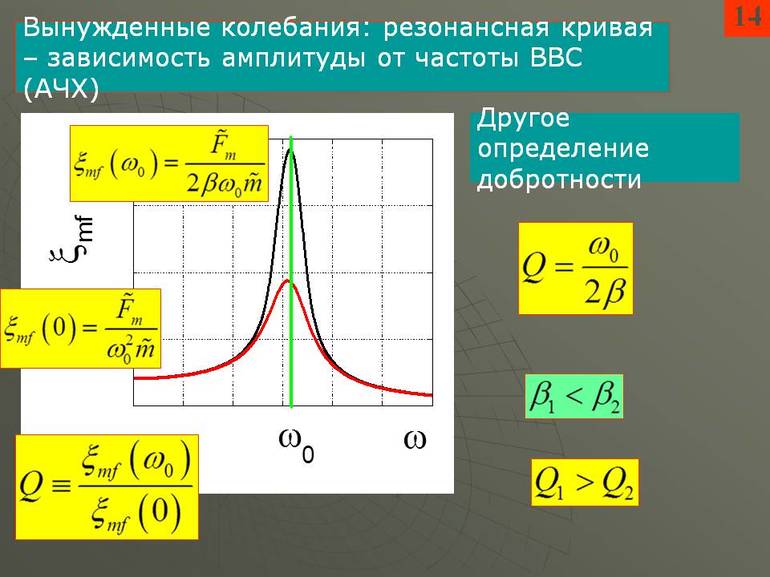
Из (1.43) видно, что при отсутствии сопротивления (в=0) амплитуда вынужденных колебаний при резонансе бесконечно большая. При этом из (1.42) следует, что резонанс в системе без затухания наступает тогда, когда частота вынуждающей силы совпадает с частотой собственных колебаний. Графическая зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы при разных значениях коэффициента затухания показана на рис. 1.12.

Механический резонанс может быть как полезным, так и вредным явлением. Вредное действие резонанса связано главным образом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать возможное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют несколько собственных частот колебаний и, соответственно, несколько резонансных частот.

Если коэффициент затухания внутренних органов человека был бы невелик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, повреждению связок и т. п. Однако такие явления при умеренных внешних воздействиях практически не наблюдаются, так как коэффициент затухания биологических систем достаточно велик. Тем не менее резонансные явления при действии внешних механических колебаний происходят во внутренних органах. В этом, видимо, одна из причин отрицательного воздействия инфразвуковых колебаний и вибраций на организм человека (см. 2.7 и 2.8).

Пожалуй, нет ни одного дня в жизни, когда бы человек не сталкивался с вынужденными колебаниями. Самый яркий пример — качели. Чтобы они закачались, необходимо применить к ним вынуждающую силу. При этом для поддержания незатухающего и периодически повторяющегося движения нужно обеспечить приток внешней энергии. Только лишь в этом случае можно избавиться от затухания и компенсировать трение.

Общие сведения

Одним из состояний тела может быть нахождение его в точке равновесия. Вывести физический объект из него возможно путём воздействия определённого направления. Другими словами, приложив силу. В итоге тело может не только изменить своё положение, но и стремится вернуться к исходному. Например, часовой маятник. Сила сжатия пружины или электромагнитное поле заставляет отклоняться его от вертикального положения в 2 стороны.

Процесс, при котором изменение состояния относительно точки равновесия повторяется во времени, называют колебательным. Он всегда связан с превращением энергии из одной формы в другую. По своей сути они напоминают распространение волн в природе, поэтому их изучением занимается волновая и колебательная теория. Единственное различие между ними, что при возникновении волны происходит перенос энергии.

Существует 3 вида основных колебаний:

1. Свободные — созданные напряжением внутренних сил после вывода из состояния равновесия произошедшего каким-либо путём. Это явление всегда затухающее, то есть с течением времени система возвращается в начальное положение. Например, грузик, подвешенный на нити, сжимание и разжимание пружины.
2. Вынужденные — поддерживающиеся колебания определённой силой периодического воздействия. Например, положение рук при ходьбе.
3. Автоколебания — движения системы, которая обладает запасом потенциальной энергии. Например, механические часы. Отличительной чертой является уход от положения равновесия из-за свойств системы, а не исходных условий.

Практически 95% периодического движения составляют свободные и вынужденные колебания. Как и любое явление, они характеризуются рядом параметров. Основные — амплитуда и частота. Первый определяет наибольшее отклонение от начального положения, а второй обозначает число колебаний за единицу времени. Обратной величиной частоты является период. Он показывает, через какое время показатели системы будут повторяться.

Колебания разделяют на гармонические и релаксационные. Первые можно описать с помощью тригонометрических функций — косинуса или синуса, то есть они являются плавными в отличие от релаксационных, сопровождающихся ускорением или замедлением.

Изображение и описание

Самым наглядным способом отображения колебаний является график функций, описывающий изменение. Для поддержания периодичности нужна внешняя сила. Подчиняется она различным законам. В простейшем случае правило имеет гармонический вид. Например, изменение силы можно описать функцией: f = F0 * cos (wt).

Чтобы составить уравнение движение, кроме вынуждающего действия, нужно учитывать 2 другие силы: квазиупругую и сопротивления. Первая направлена к центру и пропорциональна расстоянию от середины до места приложения: F = c * r, где c — постоянная составляющая. При этом тело получает потенциальную энергию: Ep = 1 / (2 *c * r 2 ). Вторая же характеризуется физической плотностью среды, где происходит колебание.

Если принять отклонения от равновесия за небольшое, сила сопротивления будет прямо пропорциональна скорости. Уравнение можно переписать: mx = -kx — rx + F0 * cos (wt). Сократив обе части равенства на cx, можно получить неоднородное уравнение линейного вида: x + 2bx + w 2 x = f*cos (wt), где f = F/m — частота; b = r/2m — коэффициент затухания; w = √‎(k/m) — частота колебаний. Решение равенства будет иметь вид: x = a*cos (wt — φ).

Изобразить гармоническое колебание, описываемое по формуле x (T) = A * cos (wt+φ) удобно, используя векторную диаграмму. Для этого нужно выполнить следующее:

1. Построить ось игрек и икс.
2. Изобразить вектор, длина которого будет равняться A. При этом он должен образовывать с осью икс угол фи.
3. Положительный угол отложить против движения часовой стрелки.
4. Определить проекции вектора на оси абсциссы и ординаты. Ими будут функции: y = A * sin (φ) и x = A * cos (φ).

Вращение вектора определяется двумя функциями: y (t) = A * sin (wt*φ) и x (t) = A * cos (wt + φ). Вынужденное колебание можно представить в виде изменения проекции на координатные линии некого вектора A. Причём модуль равняется амплитуде и вращается со скоростью φ, образуя в исходный момент времени с осью игреков φ0.

Кроме векторного способа, для описания колебаний применяют метод, называемый фазовой плоскостью. Его суть заключается в использовании величины x (t) и её первой производной. В этом случае движения представляют в виде системы: x (t) = A*cos (wt + φ); x'(t) = -A w 0*sin (wt + φ). По своему смыслу эти 2 уравнения описывают параметрическое движение по эллипсу. Точка будет двигаться по нему и полуосям: a = A; b = Aw.

Явление резонанса

При колебаниях может наступить момент приближения частоты вынуждающего воздействия к собственной частоте движения системы. В этом случае физики говорят, что установился резонанс. Другими словами, происходит амплитудное возрастание вынужденных колебаний при равенстве циклической частоты, которую называют резонансной. На графике зависимостей A от w кривая, описывающая явление, имеет наибольшую величину.

Амплитуду можно вычислить по формуле: A = F/2 gm √(‎ w 2 — g), где g — коэффициент затухания, то есть чем больше g, тем более будет сдвинут максимум к нулевой отметке на графике. Лучше проявляется резонанс в системах, характеризующихся малым затуханием. В ином случае циклическая частота будет мнимой, а амплитуда — монотонно уменьшаться.

Описывать колебательную систему можно через добротность (Q). Эта величина определяется из отношения энергии, которую удалось накопить, к значению её расхода за один период. С помощью этого параметра определяют качество, так как чем добротность больше, тем меньше система теряет энергию. Для любого механического периодичного движения её можно вычислить так: Q = √ (m * k) / r = (w * m) / r, где: m — масса системы, k — жёсткость, r — сопротивление.

В качестве нежелательного примера резонанса при вынужденных колебаниях можно привести работу двигателя внутреннего сгорания. В нём имеется коленчатый вал, на который оказывает воздействие шатун. При этом период изменения сил зависит от угловой скорости вращения вала. Вызываются колебания, которые при резонансе приводят к повышению напряжения оси и в дальнейшем вызывают её поломку, поэтому для борьбы с резонансом используют различные поглощающие материалы.

При помощи явления можно выделить или даже усилить довольно слабые периодические колебания. В радиотехнике его используют для получения полезного сигнала, усиления звука. Что интересно, впервые о резонансе заговорил Галилео Галилей в 1602 году, исследуя движения маятников и музыкальных струн. Он предположил, что резонанс — это отклик на силу извне, при котором происходит синхронизация частот колебаний с воздействующей на неё внешней силы. Это явление приводит к росту амплитуды движения всей системы.

Ширина кривой

При резонансе амплитуда колебаний максимальная. Следовательно, и энергия, запасённая системой, будет наибольшей. Она может быть равной: E = (½) * (mw 2 A 2 ). Отсюда следует, что резонансную энергию возможно вычислить по формуле: E = (½) * (mw 2 * A рез 2 ), причём Арез = F / (m * 2w). Стоит только изменить частоту вынуждающей силы, то есть её уменьшить или увеличить, амплитуда колебаний резко упадёт. Если система будет высокодобротной, при небольшом смещении энергия уменьшится.

Пусть w1 и w2 частоты, на которых E будет составлять половину от значения, присущего резонансу. Можно составить систему из двух уравнений: E (w1) = (1 / 2) * (m * w1 2 * A 2 (w1)) и E (w2) = (1 / 2) * (m * w2 2 * A 2 (w2)).

Выражения A 2 (w1) и A 2 (w2) являются амплитудами при отстройке от резонанса. Связь их с A (w) будет следующей: (1 / 2) * (m * w12 2 * A 2 (w12) = (1 / 2) * (1 / 2) * (m * w0 2 * A 2 рез). В полученном равенстве можно сократить массы, число ½ и учитывая, что при высокой добротности w1 ≈ w 2 ≈ w0, убрать из формулы частоты. В итоге получится уравнение: A 2 (w12) = (½) * Aрез. После извлечения корня зависимость примет вид:

• A (w1) = (1 / √ 2) * Aрез;
• A (w1) = (1 / √ 2) * Aрез.

Разность w1 и w2 будет называться половинчатой шириной резонансной кривой, то есть коэффициент затуханий можно найти как a = Δw/2. Измерив ширину кривой, можно узнать фундаментальную характеристику колебательной системы — коэффициент затухания.

Через это определение легко вычислить и добротность. Она равняется: Q = w0 / 2a. Чтобы её найти, необходимо центральную частоту разделить на ширину резонансной кривой: Q = w0 / Δw. Получается, что чем выше будет добротность колебательной системы, тем уже резонансная кривая.

В качестве примера вынужденных колебаний механического типа можно привести язычковый частотомер. Это прибор, работа которого основана на использовании резонанса. Устройство его состоит из электромагнита, над которым располагаются металлические пластины, разные по длине. Под действием поля они начинают колебаться. В сети частота тока 50 Гц, если создаётся вынуждающая сила на 100 Гц, язычок, настроенный на это значение, начинает резонировать.

Электромагнитный резонанс позволяет выделять радиостанцию. Ещё из ярких примеров вынужденных колебаний можно отметить: движение мембраны телефона, ход иглы швейной машинки и поршня в цилиндре автомобиля, компенсацию возмущений едущего по неровной дороге авто за счёт рессоры, океанические приливы под действием Луны.

Читайте также:

  
• Ионно координационная полимеризация реферат
  
• Методы поиска инновационных идей реферат
  
• Роль массажа и самомассажа в укреплении здоровья реферат
  
• Реферат на тему технологический прогресс
  
• Курская битва реферат список литературы